Simple and Compound Interest ICSE Class-8th Concise Selina Mathematics Solutions Chapter-9 . We provide step by step Solutions of Exercise / lesson-9 Simple and Compound Interest forICSE Class-8 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-9 A, Exe-9 B and Exe-9 C to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-8.
Simple and Compound Interest ICSE Class-8th Concise Selina Mathematics Solutions Chapter-9
–: Select Topics :–
Exercise – 9 A Simple and Compound Interest
Question 1 :-
Find the interest and the amount on:
(i) ₹ 750 in 3 years 4 months at 10% per annum.
(ii) ₹ 5,000 at 8% per year from 23rd December 2011 to 29th July 2012.
(iii) ₹ 2,600 in 2 years 3 months at 1% per month.
(iv) ₹ 4,000 in 1
Answer :-
Question 2 :-
Rohit borrowed Rs. 24,000 at 7.5 percent per year. How much money will he pay at the end of 4th years to clear his debt?
Answer :-
Principal (P) = Rs.24,000
Rate (R) = 7.5% P.A.
Time (T) = 4 years
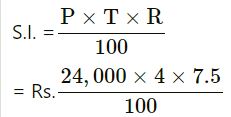
= Rs. 240 × 4 × 7.5
= 240 × 30
= Rs. 7200
Amount needed to clear the debt at the end of 4th year
= Rs. 24000 + Rs. 7200 = Rs. 3,1200
Question 3 :-
The interest on a certain sum of money is Rs. 1,480 in 2 years and at 10 percent per year. Find the sum of money.
Answer :-
Let P = Rs. x
Time (T) = 2 years
Rate (R) = 10%
x/5= Rs. 14810 ….(Given)
∴ x = 1480 × 5 = Rs. 7400
Hence the money Rs. 7400
Question 4 :-
On what principal will the simple interest be Rs. 7,008 in 6 years 3 months at 5% per year?
Answer :-
Let Principal = Rs. P
Time (T) = 6 years 3 months = 6 year +3/12
year =75/12=25/4 year =6 (1/4) years
Rate (R) = 5%
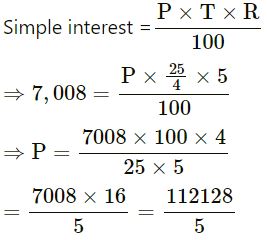
= Rs. 22425.60
Question 5 :-
Find the principal which will amount to Rs. 4,000 in 4 years at 6.25% Per annum.
Answer :-
Let Principal = Rs. P, Time (T) = 4 years
= 4 × 800
⇒ P = Rs. 3200
Hence principal = Rs. 3200
Question 6 :-
(i) At what rate per cent per annum will Rs. 630 produce an interest of Rs. 126 in 4 years ?
(ii) At what rate per cent per year will a sum double itself in 6
Answer :-
(i)
P = Rs. 630, I = Rs. 126, T = 4 years
(ii)
Let P = Rs. 100
∴ Amount = 2 × Rs. 100 = Rs. 200
Interest = A − P
= Rs. 200 − Rs. 100
= Rs. 100
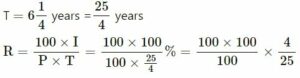
= 16%
Question 7 :-
(i) In how many years will Rs.950 produce Rs.399 as simple interest at 7%?
(ii) Find the time in which Rs.1200 will amount to Rs.1536 at 3.5% per year.
Answer :-
(i)
P = Rs.950
S.I. = Rs.399
R = 7%
We know that :
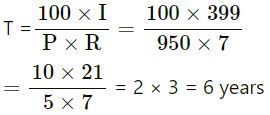
(ii)
A = Rs.1536
P = Rs.1200
I = A − P
= Rs.1536 − Rs.1200
= Rs.336
We know that :
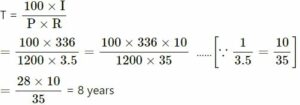
Question 8 :-
The simple interest on a certain sum of money is 
Answer :-
Let P = Rs.8
S.I. = Rs. (3/8)×8
= Rs.3
T =6 (1/4) years = 25/4 years
We know that :
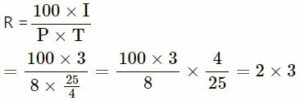
= 6%
Question 9 :-
What sum of money borrowed on 24th May will amount to Rs. 10210.20 on 17th October of the same year at 5 percent per annum simple interest.
Answer :-
A = Rs. 10210.20
R = 5% P.A.
T=May + June + July + August + Sept.+ Oct.
= 7 + 30 + 31 + 31 + 30 + 17
= 146/365 days = 2/5 year
We know that :
P + I = A
⇒ P = Rs.10010
∴ Money to be borrowed = Rs.10010
Question 10 :-
In what time will the interest on a certain sum of money at 6% be 
Answer :-
Let P = Rs.8
Interest = Rs.8 × 5/8 = Rs.5
R = 6%
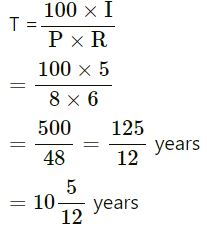
= 10 years 5 months
∴ Time = 10 years 5 months
Question 11 :-
Ashok lent out Rs.7000 at 6% and Rs.9500 at 5%. Find his total income from the interest in 3 years.
Answer :-
case I :
P = Rs.7000
R = 6%
T = 3 years
= Rs.1260
case II :
P = Rs.9500
R = 5%
T = 3 years
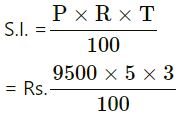
= Rs.1425
Total income from the interest
= Rs.1260 + Rs.1425
= Rs.2685
Question 12 :-
Raj borrows Rs.8,000; out of which Rs. 4500 at 5% and the remainder at 6%. Find the total interest paid by him in 4 years.
Answer :-
Total sum borrowed by Raj = Rs.8000
In First Case :
P = Rs.4500
R = 5%
T =4 years
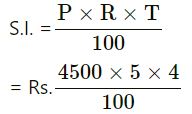
= Rs.900
In Second Case :
p = Rs.8000 − Rs.4500
= Rs.3500
R = 6%
T = 4 years
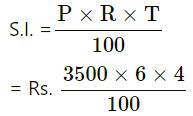
= 35 × 6 × 4 = Rs.840
Total interest paid by Raj
= Rs.900 + Rs.840
= Rs.1740
Question 13 :-
Mohan lends Rs.4800 to John for 4
Answer :-
In first case :
P = Rs.4800
R = x% (Suppose)
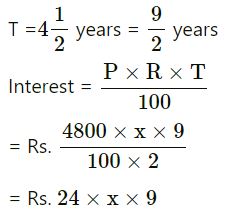
= Rs.216x
In second case :
P = Rs.2500
R = x%
T = 6 years
= Rs.150x
According to statement,
Interest in first case + Interest in second case
= Rs.2196
∴ Rs.216x + Rs.150x = Rs.2196
⇒ Rs.366x = Rs.2196
⇒ x =2196/366
⇒ x = 6
∴ Rate = 6%
Question 14 :-
John lent Rs. 2550 to Mohan at 7.5 percent per annum. If Mohan discharges the debt after 8 months by giving an old black and white television and Rs. 1422.50; find the price of the television.
Answer :-
Exercise – 9 B ICSE Class-8th Concise Selina Mathematics
Question 1 :-
The interest on a certain sum of money is 0.24 times of itself in 3 years. Find the rate of interest.
Answer :-
Question 2 –
If ₹ 3,750 amount to ₹ 4,620 in 3 years at simple interest. Find:
(i) the rate of interest
(ii) the amount of Rs. 7,500 in 5
Answer :-
(i) A = Rs.4620
P = Rs.3750
I = A − P = Rs.4620 − Rs.3750 = Rs.870
T = 3 years
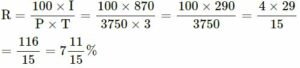
(ii) P = Rs.7500
R = 116/15 %
T =5 (1/2) years = 11/2 years
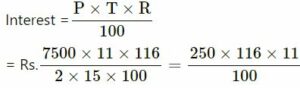
= 10 × 29 × 11 = 290 × 11 = Rs.3190
Amount = Rs.7500 + 3190 = Rs.10,690
Question 3 :-
A sum of money, lent out at simple interest, doubles itself in 8 years. Find :
(i) the rate of interest
(ii) in how many years will the sum become triple (three times) of itself at the same rate percent?
Answer :-
Let P = Rs.100, A = Rs.200
I = Rs.200 − Rs.100 = Rs.100, T = 8 years
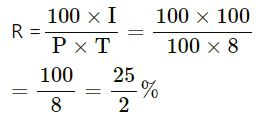
Now again P = Rs.100
A = Rs.300
I = Rs.300 − Rs.100 = Rs.200
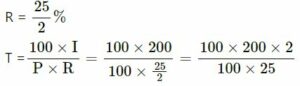
= 16 Years
So the given sum of money will become triple in 16 years.
Question 4 :-
Rupees 4000 amount to Rs.5000 in 8 years ; in what time will Rs.2100 amount to Rs.2800 at the same rate ?
Answer :-
First case :
A = Rs.5000
P = Rs.4000
I = A − P
= Rs.5000 − Rs.4000
= Rs.1000
T = 8 years
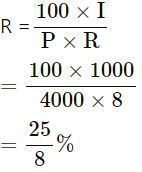
Second Case :
A = Rs.2800
P = Rs.2100
I = Rs.2800 − Rs.2100 = Rs.700
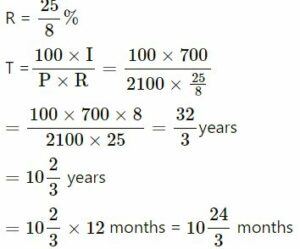
= 10 years 8 months
Question 5 :-
What sum of money lent at 6.5% per annum will produce the same interest in 4 years as Rs.7500 produce in 6 years at 5% per annum?
Answer :-
First case :
P = Rs.7500
R = 5%
T = 6 years
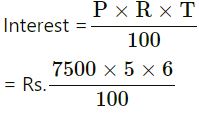
= Rs.75 × 5 × 6
= Rs.2250
Second case:
According to the statement, interest = Rs.2250
R = 6.5% P.A.
T = 4 years
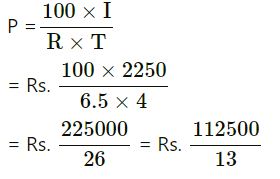
= Rs.8653.85
Required principal = Rs.8653.85
Question 6 :-
A certain sum amounts to Rs.3825 in 4 years and to Rs.4050 in 6 years. Find the rate percent and the sum.
Answer :-
In 6 years sum amounts to = Rs.4050
In 4 years sum amounts to = Rs.3825
∴ Interest of 2 years = Rs.4050 − Rs.3825 = Rs.225
The interest of 4 years = Rs.(225/2)×4
= Rs.450 …(∵ Rs.225 is interest for 2 years)
Now P = A − I
= Rs.3825 − Rs.450
= Rs.3375
I = Rs.450
T = 4 years
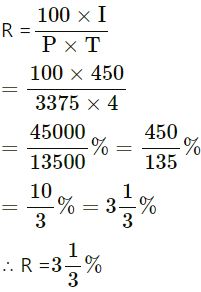
P = Rs.3375
Question 7 :-
At what rate percent of simple interest will the interest on Rs.3750 be one-fifth of itself in 4 years? To what will it amount in 15 years?
Answer :-
P = Rs.3750
I = Rs.3750×1/5 = Rs.750
T = 4 years
= 5%
Again, P = Rs.3750
The interest of 4 years = Rs.750
= Rs.2812.50
Amount in 15 years will be = Rs.3750 + Rs.2812.50
= Rs.6562.50
∴ Rate = 5%
The amount in 15 years will be = Rs.6562.50
Question 8 :-
On what date will ₹ 1950 lent on 5th January 2011 amount to ₹ 2125.50 at 5 percent per annum simple interest?
Answer :-
P = Rs.1950
A = Rs.2125.50
R = 5% P.a.
I = A − P
= Rs.2125.50 − Rs,1950
= Rs.175.50
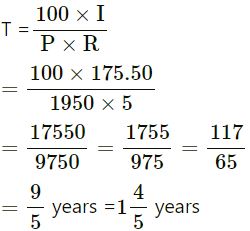
= 1 years 292 days
∵ 4/5 years
=(4/5)×365 days = 292 days
Jan. + Feb. + March + April + May + June + July +Aug. + Sept. + Oct.
(31 − 5) + 29 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 23
= 292 days
∴ Required date = 23rd October 2012
Question 9 :-
If the interest on Rs.2400 is more than the interest on Rs.2000 by Rs.60 in 3 years at the same rate percent; find the rate.
Answer :-
First case :
P = Rs.2400
R = x% (Assume)
T = 3 years
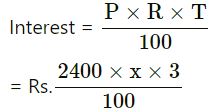
= Rs.72x
Second case :
P = Rs.2000
R = x% ….(Rate same as in first case)
T = 3 years
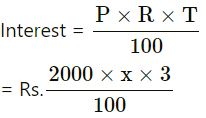
= Rs.60x
According to the statement,
72x = 60x + 60
⇒ 72x − 60x = 60
⇒ 12x = 60
⇒ x =60/12
⇒ x = 5
∴ Rate = 5%
Question 10 :-
Divide Rs. 15,600 into two parts such that the interest on one at 5 percent for 5 years may be equal to that on the other at 4
Answer :-
Let one part = Rs. x
∴ Second part = Rs. (15,600 − x)
By the given condition
⇒ 25x = 27 × 15,600 − 27x
⇒ 25x + 27x = 27 × 15,600
⇒ 52x = 27 × 15,600
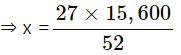
= 27 × 300
= 8100
Hence one part = Rs.8100 and second part Rs. (15,600 − 8,100) = Rs.7,500
Exercise – 9 C Simple and Compound Interest ICSE Mathematics Class-8th Concise Selina Solutions
Question 1 :-
A sum of Rs. 8,000 is invested for 2 years at 10% per annum compound interest. Calculate:
(i) interest for the first year.
(ii) principal for the second year.
(iii) interest for the second year.
(iv) final amount at the end of second year
(v) compound interest earned in 2 years.
Answer :-
(i) Here Principal (P) = Rs. 8,000
Rate of interest = 10%
= Rs.800
(ii) ∴ Amount = Rs.8,000 + Rs.800 = Rs.8,800
Thus Principal for the second year = Rs.8,800
(iii) Interest for the second year
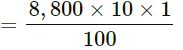
= Rs.880
(iv) Amount at the end of second year = Rs.8,800 + Rs.880 = Rs.9,680
(v) Hence compound interest earned in 2 years
= Rs.9,680 − Rs.8,000 = Rs.1680
Question 2 :-
A man borrowed Rs. 20,000 for 2 years at 8% per year compound interest. Calculate :
(i) the interest of the first year.
(ii) the interest of the second year.
(iii) the final amount at the end of second year.
(iv) the compound interest of two years.
Answer :-
Here Principal (P) =Rs.20,000, Time = 1 year
Rate = 8%
(i) ∴ The interest of the first year =(20,000×8×1)/100
= Rs.1600
(ii) ∴ Amount after one year
i.e. Principal for second year = Rs.20,000 + Rs.1,600 = Rs.21,600
∴ Interest for second year =(21,600×8×1)/100
= 216 × 8
= Rs.1728
(iii) Final amount at the end of second year
= Rs. (21,600 + 1728) = Rs.23,328
(iv) Interest of two years = Rs.23,328 − Rs.20,000 = Rs.3,328
Question 3 :-
Calculate the amount and the compound interest on Rs. 12,000 in 2 years and at 10% per year.
Answer :-
In Ist year
Principal (P) = Rs.12,000
Rate (R) = 10%
Time (T) = 1 year
I = Interest =(12,000×10×1)/100
= 120 × 10
= Rs.1200
Amount = P + I = Rs.12,000 + Rs.1200 = Rs.13,200
In IInd year
P = Rs.13,200, R = 10%, Time (T) = 1 year
∴ Interest =(13,200×10×1)/100 = 132 × 10
= Rs.1320
∴ Amount in 2 years = Rs. (13,200) + (1320)
= Rs.14520
Compound interest in 2 years = Rs.1200 + Rs.1320 = Rs.2520
[or directly = Rs.14520 − Rs.12000 = Rs.2520]
Question 4 :-
Calculate the amount and the compound interest on Rs. 10,000 in 3 years at 8% per annum.
Answer :-
In I st year
Principal (P) = Rs.10,000,
Rate (R) = 8%
Time (T) = 1 year
∴ Interest = (10,000×8×1)/100
= 100 × 8
= Rs.800
In II nd year
P = Rs.10,000 + Rs.800 = Rs.10,800
Rate (R) = 8%,
Time (T) = 1 year
∴ Interest =(10,800×8×1)/100
= 108 × 8
= Rs.864
In III rd year
∴ P = Rs.10,800 + Rs.864 = Rs.11664,
R = 8%, T = 1 year
∴ Interest =(11664×8×1)/100 = (11664×2)/25
= Rs.933.12
∴ Amount = Rs.11664+ 933.12 = Rs.12597.12
Hence required amount = Rs.12597.12
∴ Compound interest = Rs.12597.12 − 10000
= Rs.2597.12
Question 5 :-
Calculate the compound interest on Rs. 5,000 in 2 years; if the rates of interest for successive years be 10% and 12% respectively.
Answer :-
In I st year
Principal (P) = Rs.5,000, Rate (R) = 10%, Time (T) = 1 year
∴ Interest =(5,000×10×1)/100 = 50 × 10 = Rs.500
∴ Amount at the end of 1st year = Rs. (5000 + 500) = Rs.5500
In II nd year
P = Rs.5550, Rate = 12%, T = 1 year
∴ Interest =(5500×12×1)/100 = 55 × 12 = Rs.660
∴ Amount at the end of 2nd year = Rs.5500 + Rs.660 = Rs.6160
Hence compound interest =Rs.6160 − Rs.5000 = Rs.1160
Question 6 :-
Calculate the compound interest on Rs. 15,000 in 3 years; if the rates of interest for successive years be 6%, 8% and 10% respectively.
Answer :-
In I st year
Principal (P) = Rs.15,000, Rate (R) = 6%, Time (T) = 1 year
∴ Interest =(15,000×6×1)/100 = 150 × 6 = Rs.900
∴ Amount at the end of 1nd year
= Rs.15,000 + Rs.900
= Rs.15900
In II nd year
P = Rs.15900, R = 8%, T = 1 year
∴ Interest =(15,900×8×1)/100 = 159 × 8 = Rs.1272
∴ Amount at the end 2nd year
= Rs. (15900 + 1272)
= Rs.17172
In III rd year
P = Rs.17172, R = 10%, T = 1 year
∴ Interest =(17172×10×1)/100 = Rs.1717.20
∴ Amount at the end of 3rd year
= Rs. (17172 + 1717.20)
= Rs.18889.20
∴ Compound interest = 18889.20 − 15,000
= Rs.3889.20
Question 7 :-
Mohan borrowed Rs. 16,000 for 3 years at 5% per annum compound interest. Calculate the amount that Mohan will pay at the end of 3 years.
Answer :-
In I st year
Principal (P) = Rs.16,000, Rate (R) = 5%, Time (T) = 1 year
∴ Interest =(16000×5×1)/100= 160 × 5 = Rs.800
∴ Amount at the end of 1st year = Rs. (16,000 + 800) = Rs.16,800
In II nd year
P = Rs.16,800, R = 5%, T = 1 year
∴ Interest =(16,800×5×1)/100 = 168 × 5 = Rs.840
∴ Amount at the end of 2nd year = Rs. (16,800 + 840) = Rs.17640
In III rd year
P = 17640, R = 5%, T = 1 year
∴ Interest =(17640×5×1)/100=17642 = Rs.882
∴ Amount at the end of 3rd year = Rs. (17640 + 882) = Rs.18522
Hence reqd. amount = Rs.18522
Question 8 :-
Rekha borrowed Rs. 40,000 for 3 years at 10% per annum compound interest. Calculate the interest paid by her for the second year.
Answer :-
In I st year
Principal = Rs.40,000, Rate = 10%, Time = 1 year
∴ Interest =(40,000×10×1)/100
= 400 × 10
= Rs.4000
∴ Amount at the end of 1st year = Rs. (40,000 + 4000) = Rs.44,000
In II nd year
P = Rs.44,000, R = 10%, T = 1 year
∴ Interest = Rs.(44,000×10×1)/100
= 440 × 10
= Rs.4400
Thus interest earned in the second year = Rs.4400
Question 9 :-
Calculate the compound interest for the second year on Rs. 15000 invested for 5 years at 6% per annum.
Answer :-
Principal (P) = Rs.15000
Rate (R) = 6% p.a.
Period (n) = 5 years
Interest for the first year =PRT/100
=(15000×6×1)/100
= Rs.900
∴ Amount for the first year = Rs.15000 + 900
= Rs.15900
Principal for the second year= Rs.15900
Interest for the second year =(15900×6×1)/100
= 159 x 6
= Rs. 954
Question 10:-
A man invests Rs. 9600 at 10% per annum compound interest for 3 years. Calculate :
(i) the interest for the first year.
(ii) the amount at the end of the first year.
(iii) the interest for the second year.
(iv) the interest for the third year.
Answer :-
Principal (P) = Rs.9600
Rate (R) = 10% p.a.
Period (n) = 3 years
(i) ∴ Interest for the first year =PRT/100
= (9600×10×1)/100
= Rs.960
(ii) Amount at the end of first year
= P + S.I.
= Rs.9600 + 960
= Rs.10560
(iii) Principal for the second year = Rs.10560
Interest for the second year = (10560×10×1)/100
= Rs.1056
∴ Amount after second year = Rs.10560 + 1056 = Rs.11616
(iv) Principal for the third year = Rs.11616
Interest for the third year = (11616×10×1)/100
= 116.16 × 10
= Rs.1161.60
Question 11 :-
A person invests Rs. 5,000 for two years at a certain rate of interest compounded annually. At the end of one year, this sum amounts to Rs. 5,600. Calculate :
(i) the rate of interest per year.
(ii) the amount at the end of the second year.
Answer :-
Principal (P) = Rs.5000
Period (T) = 2 years
Amount at the end of one year = Rs.5600
∴ Interest for the first year = A − P
= Rs.5600 − 5000
= Rs.600
(i) ∴ Rate of interest =(S.I.×100)/(P×T)
=(600×100)/(5000×1)
= 12% p.a.
(ii) Principal for the second year = Rs.5600
Interest for the second year = (5600×12×1)/100
= ₹672
∴ Amount at the end of the second year
= P + S.I.
= 5600 + 672
= ₹ 6272
Question 12 :-
Calculate the difference between the compound interest and the simple interest on ₹ 7,500 in two years and at 8% per annum.
Answer :-
Principal (P) = ₹7500
Rate (R) = 8% p.a.
Period (T) = 2 years
∴ Simple interest =(PRT/100) = (7500×8×2)/100
= ₹1200
Interest for the first year = (7500×8×1)/100
= ₹600
∴ Amount at the end of first year = P + S.I.
= ₹7500 + ₹600
= ₹8100
Principal for the second year = ₹8100
∴ Interest for the second year = (8100×8×1)/100
= ₹648
∴ Total C.I. for 2 years = ₹600 + ₹648
= ₹1248
∴ Difference between C.I. and S.I. for 2 years
= ₹1248 − ₹1200
= ₹48
Question 13 :-
Calculate the difference between the compound interest and the simple interest on ₹ 8,000 in three years and at 10% per annum.
Answer :-
Principal (P) = ₹8000
Rate (R) = 10% p.a.
Period (T) = 3 years
∴ S.I. for 3 years = (PRT/100) = (8000×10×3)/100
= ₹2400
Now, S.I. for 1st year = ₹(8000×10×1)/100
= 80 × 10 × 1
= ₹800
Amount for the first year = P + S.I.
= ₹8000 + ₹800
= ₹8800
Principal for the second year = ₹8800
Interest for the second year = (8800×10×1)/100
= ₹880
∴ Amount after second year = ₹8800 + ₹880
= ₹9680
Principal for the third year = ₹9680
Interest for the third year
= ₹ (9680×10×1)/100
= ₹968
∴ C.I. for 3 year = ₹800 + ₹880 + ₹968
= ₹2648
∴ Difference between C.I. and S.I. for 3 year
= ₹ 2648 − ₹2400
= ₹ 248
Question 14 :-
Rohit borrowed ₹ 40,000 for 2 years at 10% per annum C.I. and Manish borrowed the same sum for the same time at 10.5% per annum simple interest. Which of these two gets less interest and by how much?
Answer :-
Sum borrowed (P) = ₹40000
Rate (R) = 10% p.a. compounded annually
Time (T) = 2 years
∴ Interest for the first year =PRT/100
= ₹ (40000×10×1)/100
= ₹ 4000
Amount after one year = ₹40000 + 4000
= ₹ 44000
Principal for the second year = ₹44000
∴ Interest for the second year
= (44000×10×1)/100
= ₹4400
∴ Compound Interest for 2 years = ₹4000 + 4400
= ₹8400
In the second case,
Principal (P) = ₹40000
Rate (R) = 10.5% p.a.
Time (T) = 2 years
∴ Simple Interest = PRT/100 = (40000×10.5×2)/100
= ₹ (40000×105×2)/100×10
= ₹8400
In both the cases, interest is same.
Question 15 :-
Mr. Sharma borrowed ₹ 24,000 at 13% p.a. simple interest and an equal sum at 12% p.a. compound interest. Find the total interest earned by Mr. Sharma in 2 years.
Answer :-
Sum borrowed (P) = ₹24000
Rate (R) = 13% p.a.
Time (T) = 2 years
In case of simple interest,
Simple interest for 2 years =PRT/100
= ₹ (24000×13×2)/100
= ₹6240
In the case of compound interest,
Interest for the first year = (24000×12×1)/100
= ₹ 2880
Amount after the first year
= ₹ 24000 + 2880
= ₹ 26880
Interest for the second year = ₹ (26880×12×1)/100
= ₹ (322560/100)
= ₹3225.60
∴ C.I. for 2 years = ₹2880 + 3225.60
= ₹6105.60
Total interest = ₹6240 + 6105.60
= ₹12345.60
Question 16 :-
Peter borrows ₹ 12,000 for 2 years at 10% p.a. compound interest. He repays ₹ 8,000 at the end of first year. Find:
(i) the amount at the end of first year, before making the repayment.
(ii) the amount at the end of first year, after making the repayment.
(iii) the principal for the second year.
(iv) the amount to be paid at the end of second year, to clear the account.
Answer :-
Sum borrowed = ₹12000
Rate (R) = 10% p.a. compound annually
Time (T) = 2 years
Interest for the first year =PRT/100
=(12000×100×1)/100
= ₹1200
(i) Amount = ₹12000 + 1200 = ₹13200
Amount paid = ₹8000
(ii) balance amount = ₹13200 − 8000 = ₹5200
(iii) ∴ Principal for the second year = ₹5200
(iv) Interest for the second year = (5200×10×1)/100
= ₹520
∴ Amount = ₹5200 + 520 = ₹5720
Question 17 :-
Gautam takes a loan of ₹ 16,000 for 2 years at 15% p.a. compound interest. He repays ₹ 9,000 at the end of first year. How much must he pay at the end of second year to clear the debt?
Answer :-
Loan taken (P) = ₹ 16000
Rate (R) = 15% p.a.
Time (T) = 2 years
∴ Interest for the first year
= PRT/100 = (16000×15×1)/100
= ₹2400
Amount after one year = ₹16000 + 2400
= ₹18400
At the end of one year amount paid back = ₹9000
Balance amount = ₹18400 − 9000
= ₹9400
Interest for the second year = (9400×15×1)/100
= ₹1410
Amount after second year = ₹9400 + 1410
= ₹10810
Question 18 :-
A certain sum of money, invested for 5 years at 8% p.a. simple interest earns an interest of ₹ 12,000. Find:
(i) the sum of money.
(ii) the compound interest earned by this money in two years and at 10% p.a. compound interest.
Answer :-
Rate (R) = 8% p.a.
Period (T) = 5 years
Interest (I) = ₹12000
(i) ∴ Sum = (I×100)/(R×T)
= ₹ (12000×100)/8×5
= ₹30000
(ii) Rate (R) = 10% p.a.
Time (T) = 2 years
Principal (P) = ₹30000
Interest for the first year = PRT/100
= ₹ (30000×10×1)/100
= ₹3000
∴ Amount after one year = ₹30000 + 3000
= ₹33000
Principal for the second year = ₹33000
Interest for the second year = (33000×10×1)/100
= ₹3300
∴ Compound Interest for two years
= ₹3000 + 3300
= ₹6300
Question 19 :-
Find the amount and the C.I. on ₹ 12,000 at 10% per annum compounded half-yearly.
Answer :-
Principal (P) = ₹12,000
Rate (r) = 10%
Time (t) = 1 years
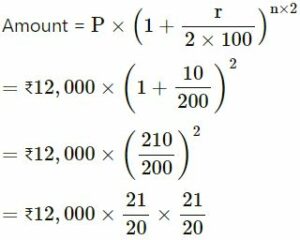
= ₹13,230
C.I. = Amount − Principal
= ₹13230 − ₹12000
= ₹1230
Question 20 :-
Find the amount and the C.I. on ₹ 8,000 in 1
Answer :-
Principal (P) = ₹8000
Rate = 20%
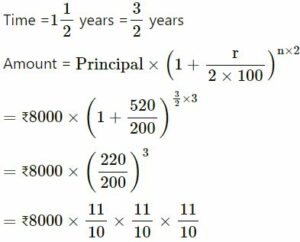
= ₹10648
C.I. = Amount − Principal
= ₹10648 − ₹8000
= ₹2648
Question 21 :-
Find the amount and the compound interest on ₹ 24,000 for 2 years at 10% per annum compounded yearly.
Answer :-
Principal (P) = ₹24,000
Time (t) = 2 years
Rate (r) = 10%
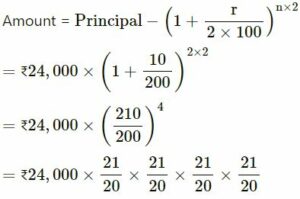
= ₹29,172
C.I. = Amount − Principal
= ₹29,172 − ₹24,000
= ₹5,172
Question 22 :-
Find the amount and the compound interest on ₹ 16,000 for 3 years at 5% per annum compounded annually.
Answer :-
Principal (P) = ₹16,000
Time (t) = 3 years
Rate (r) = 5%
= ₹18,555
C.I. = Amount − Principal
= ₹18,555 − ₹16,000
= ₹2555
Question 23 :-
Find the amount and the compound interest on ₹ 20,000 for 1
Answer :-
Principal (P) = ₹20,000
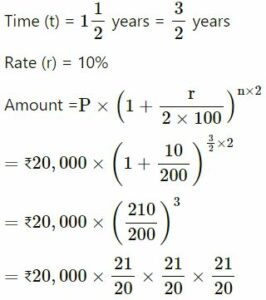
= ₹23,152.50
C.I. = Amount − Principal
= ₹23,152.50 − ₹20,000
= ₹3,152.50
Question 24 :-
Find the amount and the compound interest on ₹ 32,000 for 1 year at 20% per annum compounded half-yearly.
Answer :-
Principal (P) = ₹32,000
Time (t) = 1 year
Rate (r) = 20%
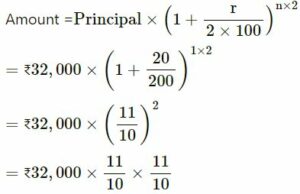
= ₹38,720
C.I. = Amount − Principal
= ₹38,720 − ₹32,000
= ₹6,720
Question 25 :-
Find the amount and the compound interest on ₹ 4,000 in 2 years, if the rate of interest for first year is 10% and for the second year is 15%.
Answer :-
Principal (P) = ₹4,000
Time (t) = 2 years
Rate (R1) = 10% and rate (R2) = 15%
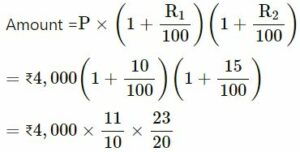
= ₹ 5060
C.I. = Amount − Principal
= ₹ 5060 − ₹4000
= ₹ 1060
Question 26 :-
Find the amount and the compound interest on ₹ 10,000 in 3 years, if the rates of interest for the successive years are 10%, 15% and 20% respectively.
Answer :-
Principal (P) = ₹10,000
Time (t) = 3 years
Rate (R1) = 10%
Rate (R2) = 15%
Rate (R3) = 20%
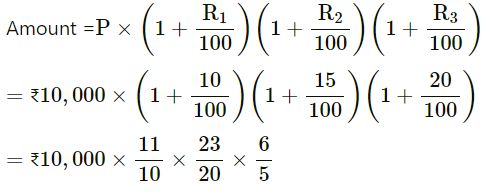
= ₹15,180
C.I. = Amount − Principal
= ₹15,180 − ₹10,000
= ₹5180
— End of Simple and Compound Interest Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -8
Thanks
