Simultaneous Linear Equations Class-9th Concise Selina ICSE Maths Solutions Chapter-6 (Including Problems). We provide step by step Solutions of Exercise / lesson-6 Simultaneous Equations (Including Problems) for ICSE Class-9 Concise Selina Mathematics by RK Bansal.
Our Solutions contain all type Questions with Exe-6 A, Exe-6 B, Exe-6 C, Exe-6 D, Exe-6 E, Exe-6 F, and Exe-6 G to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics .
Simultaneous Linear Equations Class-9th Concise Selina ICSE Maths Solutions Chapter-6 (Including Problems)
–: Select Topics :–
Simultaneous Linear Equations (Including Problems) Class-9th Concise Selina ICSE Maths Solutions Exercise – 6(A)
Question 1
Solve the following pair of linear (simultaneous) equation by the method of elimination by substitution :
8x + 5y = 9
3x + 2y = 4
Answer
8x + 5y = 9 …(1)
3x + 2y = 4 …(2)
8x + 5y = 9
∴ 5y = 9 – 8x
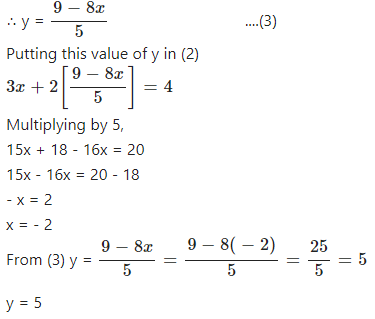
Question 2
Solve the pair of linear (simultaneous) equation by the method of elimination by substitution :
2x – 3y = 7
5x + y= 9
Answer
2x – 3y = 7 …(1)
5x + y = 9 …(2)
5x + y = 9
∴ y = 9 – 5x …(3)
Putting this value of y in (1)
2x – 3 (9 – 5x) = 7
∴ 2x – 27 + 15x = 7
∴ 2x + 15x = 7 + 27
∴ 17x = 34
∴ x = 2
From (2)
y = 9 – 5(2)
y = -1
Question 3
Solve the pair of linear (simultaneous) equation by the method of elimination by substitution:
2x + 3y = 8
2x = 2 + 3y
Answer
2x + 3y = 8 …(1)
2x = 2 + 3y …(2)
2x = 2 + 3y
Putting this value of 2x in (1)
2 + 3y + 3y = 8
∴ 6y = 8 – 2
∴ 6y = 6
∴ y = 1
From (2) 2x = 2 + 3(1)
x = 52
x = 2.5
Question 4
Solve the following pair of linear (simultaneous) equation by the method of elimination by substitution:
0.2x + 0.1y = 25
2(x – 2) – 1.6y = 116
Answer
The given pair of linear equations are
0.2x + 0.1y = 25 ….(1)
2( x – 2 ) – 1.6y = 116 …..(2)
Consider equation (1)
0.2x + 0.1y = 25
⇒ 0.2x = 25 – 0.1y
⇒ x = 25-0.1y0.2 ….(3)
Substitute the value of x from equation (3) in equation (2).
2( x – 2 ) – 1.6y = 116

Question 5
Solve the pair of linear (simultaneous) equation by the method of elimination by substitution:
6x = 7y + 7
7y – x = 8
Answer
6x = 7y + 7 …(1)
7y – x = 8 …(2)
7y – x = 8
∴ x = 7y – 8
Putting this value of x in (1)
6( 7y – 8 ) = 7y + 7
∴ 42y – 48 = 7y + 7
∴ 35y = 55
∴ y = 117
From (2)
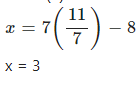
Question 6
Solve the pair of linear (simultaneous) equation by the method of elimination by substitution :
y = 4x – 7
16x – 5y = 25
Answer
y = 4x – 7 ….(1)
16x – 5y = 25 ….(2)
y = 4x – 7
Putting this value of y in (2)
∴ 16x – 5 (4x – 7) = 25
∴ 16x – 20x + 35 = 25
∴ – 4x = – 10
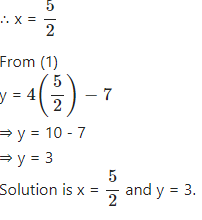
Question 7
Solve the pair of linear (simultaneous) equation by the method of elimination by substitution:
2x + 7y = 39
3x + 5y = 31
Answer
2x + 7y = 39 …(1)
3x + 5y = 31 …(2)
2x + 7y = 39

Question 8
Solve the following pair of linear (simultaneous) equation by the method of elimination by substitution:
1.5x + 0.1y = 6.2
3x – 0.4y = 11.2
Answer
The given pair of linear equations are
1.5x + 0.1y = 6.2 …(1)
3x – 0.4y = 11.2 …(2)
Consider equation (1)
1.5x + 0.1y = 6.2
⇒ 1.5x = 6.2 – 0.1y
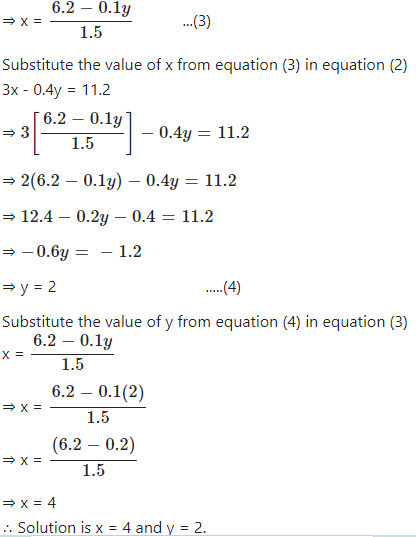
Question 9
Solve the following pair of linear (Simultaneous ) equation using method of elimination by substitution :
2( x – 3 ) + 3( y – 5 ) = 0
5( x – 1 ) + 4( y – 4 ) = 0
Answer
Given equations are
2( x – 3 ) + 3( y – 5 ) = 0 …(1)
5( x – 1 ) + 4( y – 4 ) = 0 …(2)
From (1), we get
2x – 6 + 3y – 15 = 0
⇒ 2x – 21 + 3y = 0
⇒ 2x = 21 – 3y
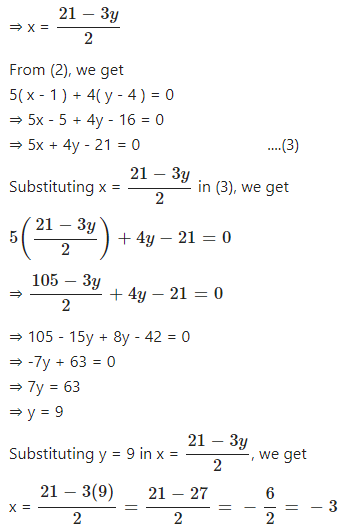
![]()
Question 10
Solve the following pair of linear (Simultaneous ) equation using method of elimination by substitution :
Answer
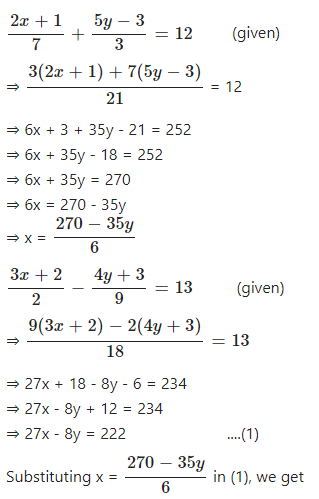

Question 11
Solve the following pair of linear (simultaneous) equation using method of elimination by substitution:
3x + 2y =11
2x – 3y + 10 = 0
Answer
3x + 2y = 11
⇒ 3x = 11 – 2y
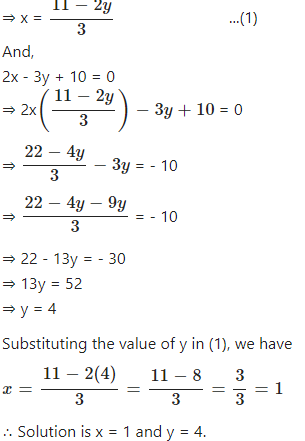
Question 12
Solve the following pair of linear (simultaneous) equation using method of elimination by substitution :
2x – 3y + 6 = 0
2x + 3y – 18 = 0
Answer
2x – 3y + 6 = 0
⇒ 2x = 3y – 6
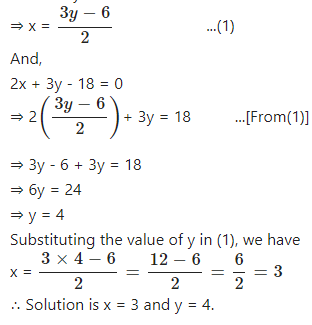
Question 13
Solve the following pair of linear (simultaneous) equation using method of elimination by substitution:
……….
Answer
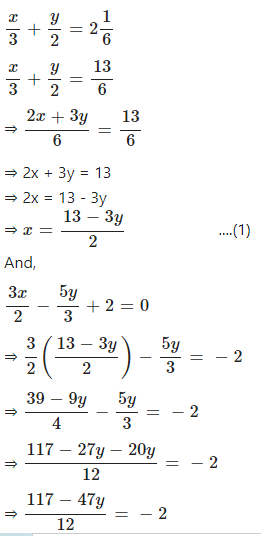
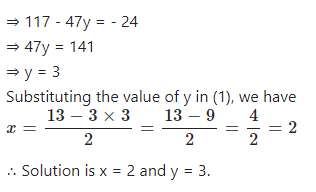
Question 14
Solve the following pairs of linear (simultaneous) equation using method of elimination by substitution:
…………
Answer
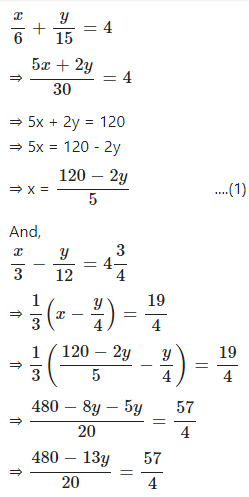
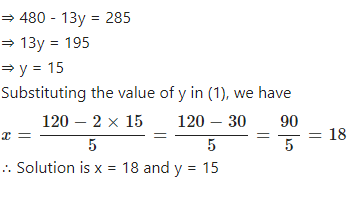
Exe-6 B Simultaneous Linear Equations (Including Problems) Class-9th Concise Selina ICSE Maths Solutions
Question 1
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :
13 + 2y = 9x
3y = 7x
Answer
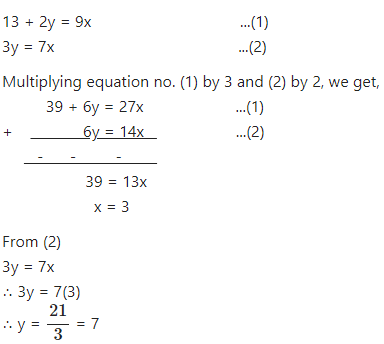
Question 2
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :
3x – y = 23
……………
Answer
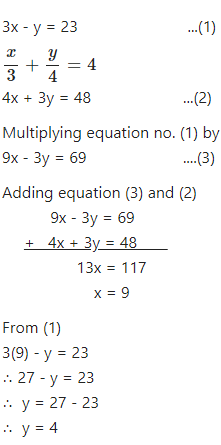
Question 3
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :
Answer
The given pair of linear equations are

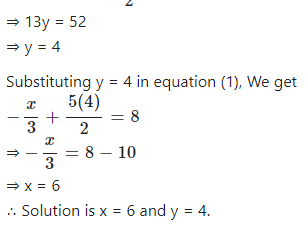
Question 4
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :
………….
Answer

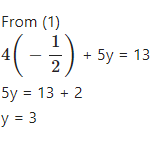
Question 5
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :
y = 2x – 6
y = 0
Answer
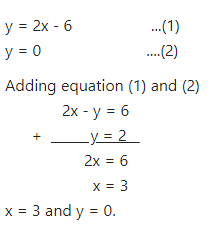
Question 6
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :……..
Answer
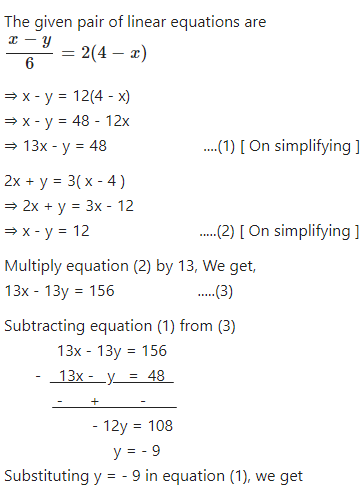
13x – ( – 9) = 48
⇒ 13x = 39
⇒ x = 3
∴ Solution is x = 3 and y = – 9
Question 7
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :
3 – (x – 5) = y + 2
2 (x + y) = 4 – 3y
Answer
3 – (x – 5) = y + 2
∴ 3 – x + 5 = y + 2
∴ – x + 8 = y + 2
∴ x + y = 6 ….(1)
2( x + y ) = 4 – 3y
∴ 2x + 2y = 4 – 3y
∴ 2x + 5y = 4 …..(2)
Multiplying equation no (1) by 2.
2x + 2y = 12 …..(3)
Subtracting equation (2) from (3)
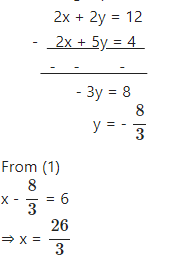
Question 8
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :
2x – 3y – 3 = 0
………..
Answer
2x – 3y – 3 = 0
⇒ 2x – 3y = 3 …..(1)
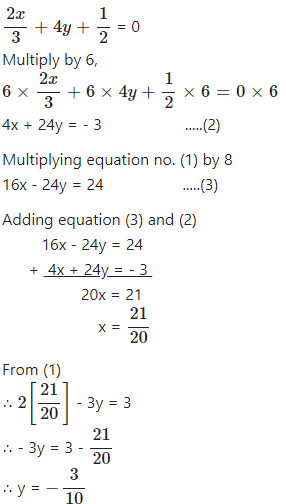
Question 9
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :
13x+ 11y = 70
11x + 13y = 74
Answer
13x + 11y = 70 …(1)
11x + 13y = 74 …(2)
Adding (1) and (2)
13x + 11y = 70
+ 11x + 13y = 74
24x + 24y = 144
Dividing by 24,
x + y = 6 ….(3)
Subtracting (2) from (1)
13x + 11y = 70
– 11x + 13y = 74
– – –
2x – 2y = – 4
Dividing by 2
x – y = – 2 ….(4)
Adding equation (3) and (4)
x – y = – 2
+ x + y = 6
2x = 4
x = 2
From (3)
2 + y = 6
y = 4
Question 10
For solving pair of equation, in this exercise use the method of elimination by equating coefficients :
41x + 53y = 135
53x + 41y = 147
Answer
41x + 53y = 135 …(1)
53x + 41y = 147 …(2)
Adding equation (1) and (2)
41x + 53y = 135
+ 53x + 41y = 147
94x + 94y = 282
Dividing by 94,
x + y = 3 ….(3)
Subtracting equation (2) from (1)
41x + 53y = 135
– 53x + 41y = 147
– – –
– 12x + 12y = – 12
Dividing by 12,
– x + y = -1 ….(4)
Adding (3) and (4)
x + y = 3
+ – x + y = -1
2y = 2
y = 1
From (3)
x + y = 3
x + 1 = 3
x = 2
Question 11
If 2x + y = 23 and 4x – y = 19; find the values of x – 3y and 5y – 2x.
Answer
2x + y = 23 …(1)
4x – y = 19 …(2)
Adding equation (1) and (2) we get,
2x + y = 23
+ 4x – y = 19
6x = 42
x = 7
From (1)
2x + y = 23
⇒ 2(7) + y = 23
⇒ 14 + y = 23
⇒ y = 23 – 14
y = 9
∴ x – 3y = 7 – 3(9) = -20
and 5y – 2x = 5(9) – 2(7) = 45 – 14 = 31.
Question 12
If 10y = 7x – 4 and 12x + 18y = 1; find the values of 4x + 6y and 8y – x.
Answer
10 y = 7x – 4
– 7x + 10y = – 4 …(1)
12x + 18y = 1 …(2)
Multiplying equation no. (1) by 12 and (2) by 7.
– 84x + 120y = – 48 ….(3)
84x + 126y = 7 ….(4)
Adding equation (3) and (4)
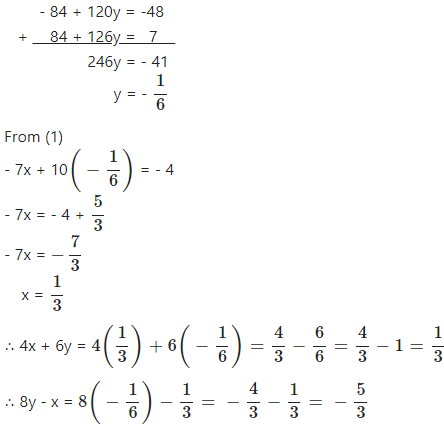
Question 13.1
Solve for x and y :
…………..
Answer

Question 13.2
Solve for x and y :
4x =………
Answer
Question 14
Find the value of m, if x = 2, y = 1 is a solution of the equation 2x + 3y = m.
Answer
Let x = 2 and y = 1 be a solution of the equation.
2x + 3y = m
⇒ 2(2) + 3(1) = m
⇒ 4 + 3 = m
⇒ m = 7
∴ If x = 2 and y = 1 is the solution of the equation
2x + 3y = m then the value of m is 7.
Question 15
10% of x + 20% of y = 24
3x – y = 20
Answer
0% of x + 20% of y = 24
⇒ 0.1x + 0.2y = 24 …..(1) [ On Simplyfying ]
3x – y = 20 …..(2)
Multiply equation (2) by 0.2, We get :
0.6x – 0.2y = 4 ……(3)
Adding equation (3) and (1)
0.6x – 0.2y = 4
+ 01x + 0.2y = 24
0.7x = 28
x = 40
Substituting x = 40 in equation (1), We get
0.1(40) + 0.2y = 24
⇒ 0.2y = 20
⇒ y = 100
∴ Solution is x = 40 and y = 100.
Question 16
The value of expression mx – ny is 3 when x = 5 and y = 6. And its value is 8 when x = 6 and y = 5. Find the values of m and n.
Answer
The value of expression mx – ny is 3 when x = 5 and y = 6.
⇒ 5m – 6n = 3 …..(1)
The value of expression mx – ny is 8 when x = 6 and y = 5.
⇒ 6m – 5n = 8 ….(2)
Multiply equation (1) by 6 and equation (2) by 5, We get:
30m – 36n = 18 ….(3)
30m – 25n = 40 …..(4)
Subtracting equation (4) from (3)
30m – 36n = 18
– 30m – 25n = 40
– + –
– 11n = – 22
n = 2
Substituting n = 2 in equation (1), we get
5m – 6(2) = 3
⇒ 5m = 15
⇒ m = 3
∴ Solution is m = 3 and n = 2.
Question 17
Solve :
11(x – 5) + 10(y – 2) + 54 = 0
7(2x – 1) + 9(3y – 1) = 25
Answer
11( x – 5 ) + 10( y – 2 ) + 54 = 0 (given)
⇒ 11x – 55 + 10y – 20 + 54 = 0
⇒ 11x + 10y – 21 = 0
⇒ 11x + 10y = 21 ….(1)
7( 2x – 1 ) + 9(3y – 1) = 25 (given)
⇒ 14x – 7 + 27y – 9 = 25
⇒ 14x + 27y – 16 = 25
⇒ 14x + 27y = 41 …..(2)
Multiplying equation (1) by 27 and equation (2) by 10, we get,
297x + 270y = 567 ….(3)
140x + 270y = 410 …..(4)
Subtracting equation (4) from equation (3), we get
157x = 157
⇒ x = 1
Substituting x = 1 in equation (1), we get,
11 x 1 + 10y = 21
⇒ 10y = 10
⇒ y = 1
∴ Solution set is x = 1 and y = 1.
Question 18
Solve :
………..
Answer
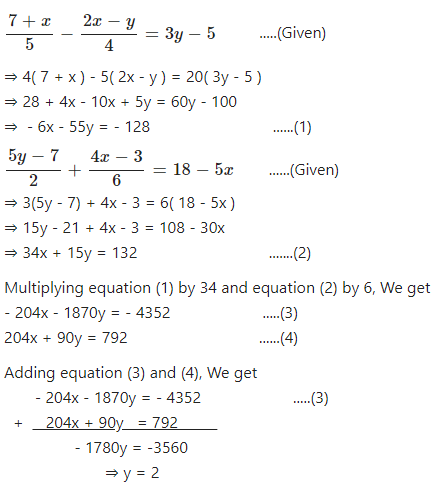
Substituting y = 2 in equation (1), We get
– 6x – 55 x 2 = – 128
⇒ – 6x – 110 = – 128
⇒ – 6x = – 18
⇒ x = 3
∴ Solution is x = 3 and y = 2.
Question 19
Solve :
Answer

Substituting x = 4 in equation (2), We get
3 x 4 + y = 8
⇒ 12 + y = 8
⇒ y = 8 – 12
⇒ y = – 4
∴ Solution is x = 4 and y = – 4
Concise Selina ICSE Class-9 Maths Solutions Simultaneous Linear Equations (Including Problems) Exe-6 C
Question 1
4x + 3y = 17
3x – 4y + 6 = 0
Answer
Given equation are 4x + 3y = 17 and 3x – 4y + 6 = 0
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 4, b1 = 3, c1 = -17 and a2 = 3, b2 = – 4, c2 = 6
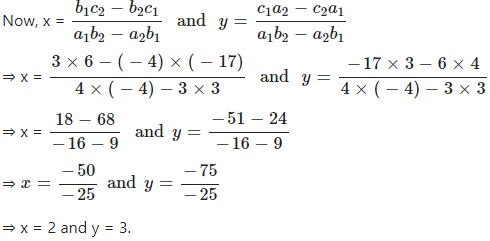
Question 2
Solve, using cross-multiplication :
3x + 4y = 11
2x + 3y = 8
Answer
Given equations are 3x + 4y = 11 and 2x + 3y = 8
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, we have
a1 = 3, b1 = 4, c1 = -11 and a2 = 2, b2 = 3, c2 = – 8
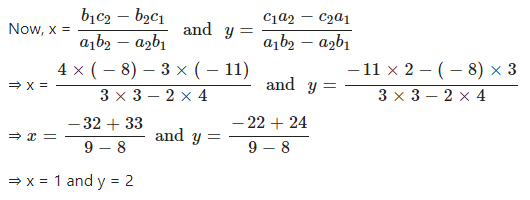
Question 3
Solve, using cross-multiplication :
6x + 7y – 11 = 0
5x + 2y = 13
Answer
Given equation are 6x + 7y – 11 = 0 and 5x + 2y = 13
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 6, b1 = 7, c1 = -11 and a2 = 5, b2 = 2, c2 = -13
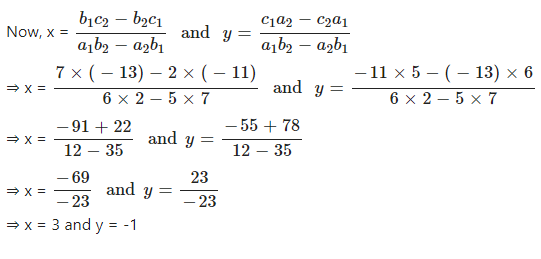
Question 4
Solve, using cross-multiplication :
5x + 4y + 14 = 0
3x = -10 – 4y
Answer
Given equation are 5x + 4y + 14 = 0 and 3x = -10 – 4y
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 5, b1 = 4, c1 = 14 and a2 = 3, b2 = 4, c2 = 10
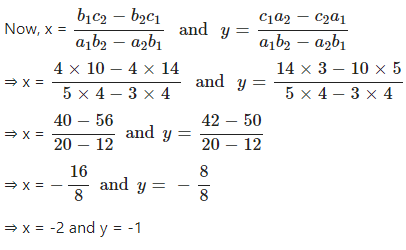
Question 5
Solve, using cross-multiplication :
x – y + 2 = 0
7x + 9y = 130
Answer
Given equation are x – y + 2 = 0 and 7x + 9y = 130
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 1, b1 = -1, c1 = 2 and a2 = 7, b2 = 9, c2 = -130

Question 6
Solve, using cross-multiplication :
4x – y = 5
5y – 4x = 7
Answer
Given equation are 4x – y = 5 and 5y – 4x = 7
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 41, b1 = – 1, c1 = – 5 and a2 = – 4, b2 = 5, c2 = – 7
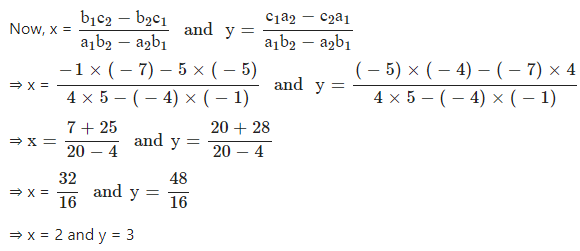
Question 7
Solve, using cross-multiplication :
4x – 3y = 0
2x + 3y = 18
Answer
Given equation are 4x – 3y = 0 and 2x + 3y = 18
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 4, b1 = – 3, c1 = 0 and a2 = 2, b2 = 3, c2 = -18

Question 8
Solve, using cross-multiplication :
8x + 5y = 9
3x + 2y = 4
Answer
Given equation are 8x + 5y = 9 and 3x + 2y = 4
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 8, b1 = 5, c1 = -9 and a2 = 3, b2 = 2, c2 = – 4
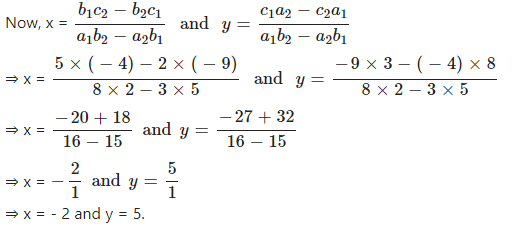
Question 9
Solve, using cross-multiplication :
4x – 3y – 11 = 0
6x + 7y – 5 = 0
Answer
Given equation are 4x – 3y – 11 = 0 and 6x + 7y – 5 = 0
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 4, b1 = – 3, c1 = -11 and a2 = 6, b2 = 7, c2 = – 5
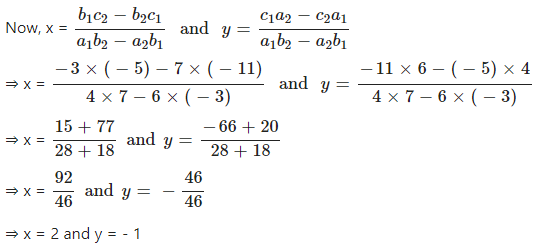
Question 10
Solve, using cross-multiplication :
4x + 6y = 15
3x – 4y = 7
Answer
Given equation are 4x + 6y = 15 and 3x – 4y = 7
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 4, b1 = 6, c1 = -15 and a2 = 3, b2 = – 4, c2 = -7

Question 11
Solve, using cross-multiplication :
0.4x – 1.5y = 6.5
0.3x + 0.2y = 0.9
Answer
Given equation are 0.4x – 1.5y = 6.5 and 0.3x + 0.2y = 0.9
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = 0.4, b1 = -1.5, c1 = -6.5 and a2 = 0.3, b2 = 0.2, c2 = 0.9
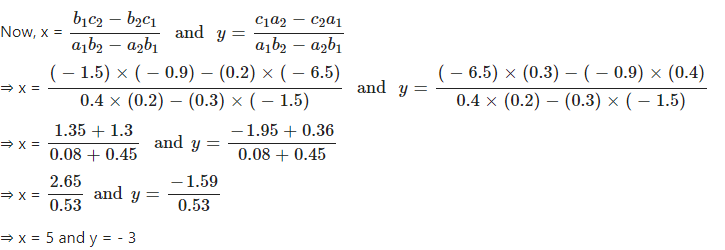
Question 12
Solve, using cross-multiplication :
√2x – √3y = 0
√5x + √2y = 0
Answer
Given equation are √2x – √3y = 0 and √5x + √2y = 0
Comparing with a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, We have
a1 = √2, b1 = √3, c1 = 0 and a2 = √5, b2 = √2, c2 = 0

Exe-6 D Simultaneous Linear Equations (Including Problems) Class-9th Concise Selina ICSE Maths Solutions
Question 1
…………………….
Answer
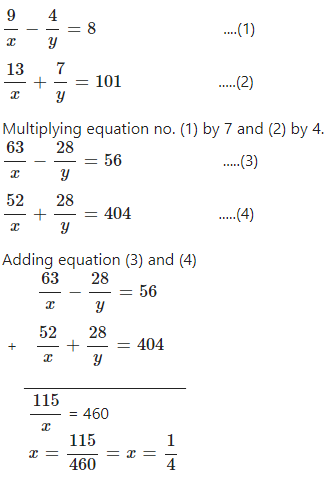
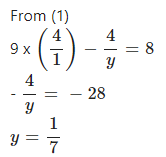
Question 2
Solve the pairs of equations :
Answer

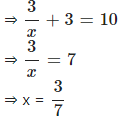
Question 3
Solve :
5x +……..
Answer
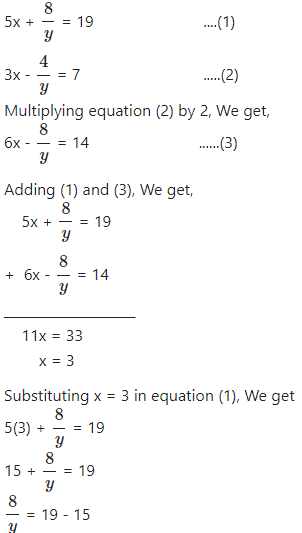
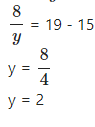
Question 4
4x + = 15 and 3x – = 7. Hence, find a if y = ax – 2.
Answer
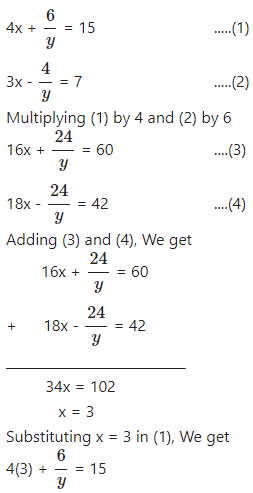
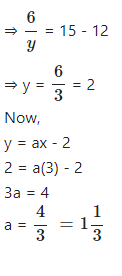
Question 5
……………………
Answer
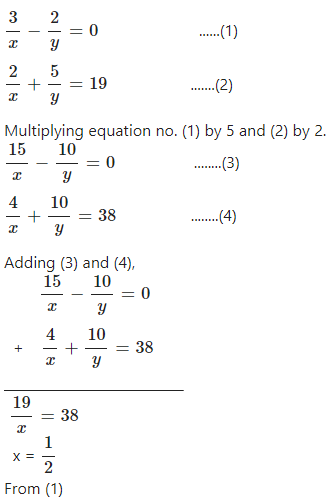
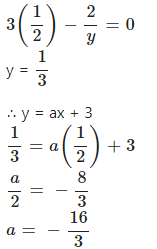
Question 6.1
Solve :
…….
Answer
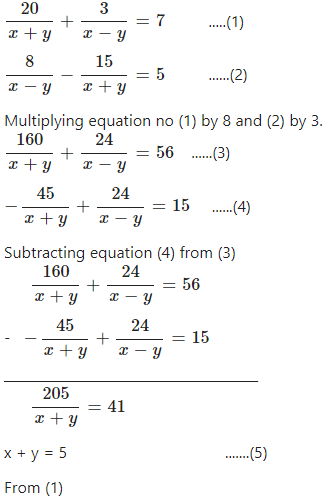
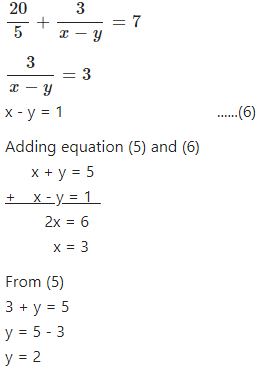
Question 6.2
Solve : ………
Answer
Let a = 3x + 4y and b = 3x – 2y
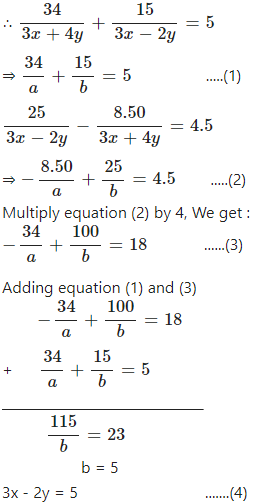
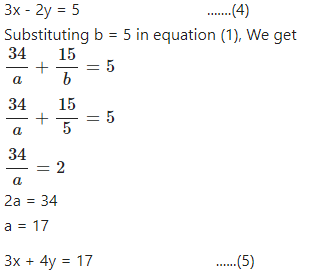
Subtracting equation (5) from (4), We get :
3x – 2y = 5
– 3x + 4y = 17
– – –
– 6y = – 12
y = 2
Substituting y = 2 in equation (4), We get
3x – 2(2) = 5
3x = 9
x = 3
x = 3
∴ Solution is x = 3 and y = 2.
Question 7.1
Solve :
x + y = 2xy
x – y = 6xy
Answer
x + y = 2xy …..(1)
x – y = 6xy ……(2)
Adding equation (1) and (2)
x + y = 2xy
+ x – y = 6xy
2x = 8xy
2 = 8y
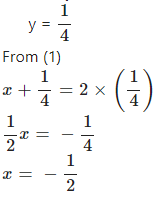
Question 7.2
Solve :
x+ y = 7xy
2x – 3y = – xy
Answer
x + y = 7xy …(1)
2x – 3 = – xy …(2)
Multiplying equation no. (1) by 3.
3x + 3y = 21xy ….(3)
Adding equation (3) and (2)
3x + 3y = 21xy
+ 2x – 3y = – xy
5x = 20xy
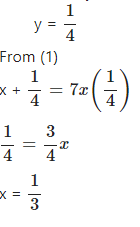
Question 8
Solve :
Answer

⇒ x =a and y = b
Solve :
…………..
x + y ≠ 0 and 2x – y ≠ 0
Answer
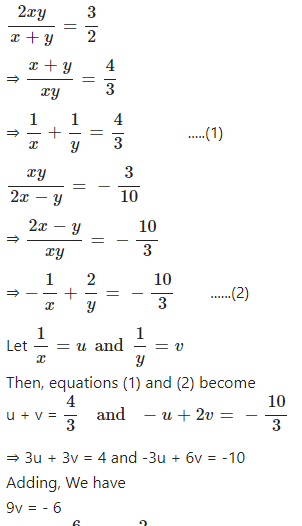
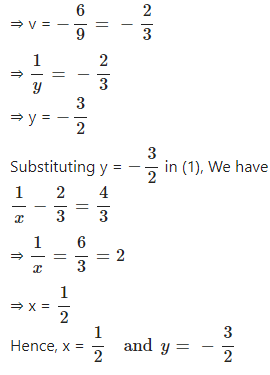
Question 10
Solve :
……..
x + y ≠ 0 and 2x – y ≠ 0
Answer
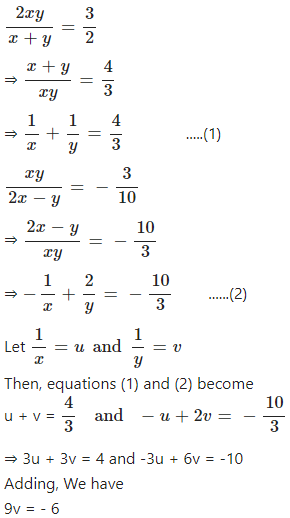
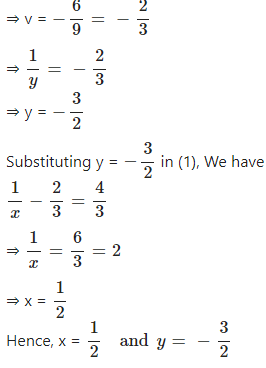
Concise Selina ICSE Class-9 Maths Solutions Simultaneous Linear Equations (Including Problems) Exercise – 6(E)
Question 1
The ratio of two numbers is . If 2 is subtracted from the first and 8 from the second, the ratio becomes the reciprocal of the original ratio. Find the numbers
Answer
Let the two numbers be x and y.
According to the question,
Let the two numbers be x and y.
According to the question,
`x/y = 2/3`
3x – 2y = 0 …..(1)
Also,`[ x – 2 ]/[ y – 8 ] = 3/2`
2x – 3y = – 20 …..(2)
Multiplying equations no. (1) by 2 and (2) by 3
6x – 4y = 0 …..(3)
6x – 9y = – 60 ……(4)
Subtracting equation (4) from (3)
6x – 4y = 0
– 6x – 9y = – 60
– + +
5y = 60
y = 12
From (1), we get
3x – 2(12) = 0
x = `24/3`
x = 8
Thus, the numbers are 8 and 12.
Question 2
Two numbers are in the ratio 4 : 7. If thrice the larger be added to twice the smaller, the sum is 59. Find the numbers.
Answer
Let the smaller number be x and the larger number be y.
According to the question,


Question 3
When the greater of the two numbers increased by 1divides the sum of the numbers, the result is . When the difference of these numbers is divided by the smaller, the result . Find the numbers.
Answer
Let the two numbers be a and b respectively such that b > a.
According to given condition,

Substituting a = 6 in equation (1), We get
2(6) – b = 3
⇒ 12 – b = 3
⇒ b = 9
Thus, the two numbers are 6 and 9 respectively.
Question 4
The sum of two positive numbers x and y (x > y) is 50 and the difference of their squares is 720. Find the numbers.
Answer
Two numbers are x and y such that x > y.
Now,
x + y = 50 ….(i)
And,
y2 – x2 = 720
⇒ (y – x)(y + x) = 720
⇒ (y – x)(50) = 720
⇒ y – x = 14.4 ….(ii)
Adding (i) and (ii), we get
2y = 64.4
⇒ y = 32.2
Substituting the value of y in (i), we have
x + 32.2 = 50
⇒ x = 17.8
Thus, the two numbers are 17.8 and 32.2 respectively.
Question 5
The sum of two numbers is 8 and the sum of their reciprocals is . Find the numbers.
Answer
Let the two numbers be x and y respectively.
Then,
x + y = 8 ….(i)
⇒ x = 8 – y
And,

⇒ xy = 15
⇒ ( 8 – y )y = 15
⇒ 8y – y2 = 15
⇒ y2 – 8y + 15 = 0
⇒ y2 – 3y – 5y + 15 = 0
⇒ y( y – 3 ) – 5( y – 3 ) = 0
⇒ ( y – 3 )( y – 5 ) = 0
⇒ y = 3 or y = 5
⇒ x = 5 or x = 3
Thus, the two numbers are 3 and 5 respectively.
Question 6
The difference between two positive numbers x and y ( x > y ) is 4 and the difference between their reciprocals is . Find the numbers.
Answer
Two numbers are x and y respectively such that x > y.
Then,
x – y = 4 ….(i)
⇒ x = 4 + y
And,
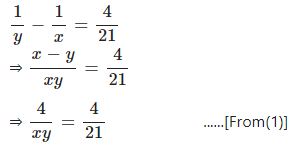
⇒ xy = 21
⇒ ( 4 + y )y = 21
⇒ 4y + y2 = 21
⇒ y2 + 4y – 21 = 0
⇒ y2 + 7y – 3y – 21 = 0
⇒ y( y + 7 ) – 3( y + 7 ) = 0
⇒ ( y – 3 )( y + 7 ) = 0
⇒ y = 3 and y = -7
We reject y = -7 since y is positive.
⇒ y = 3
⇒ x = 4 + y = 4 + 3 = 7
Thus, the two numbers are 7 and 3 respectively.
Question 7
Two numbers are in the ratio 4:5. If 30 is subtracted from each of the numbers, the ratio becomes 1:2. Find the numbers.
Answer
Let the common multiple between the numbers be x.
So, the numbers are 4x and 5x.
According to the question,
![]()
⇒ 8x – 60 = 5x – 30
⇒ 3x = 30
⇒ x = 10
So, 4x = 4(10) = 40 and 5x = 5(10) = 50
Thus, the numbers are 40 and 50.
Question 8
If the numerator of a fraction is increased by 2 and denominator is decreased by 1, it becomes . If the numerator is increased by 1 and denominator is increased by 2, it becomes . Find the fraction.
Answer
Let the numerator and denominator a fraction be x and y respectively .
According to the question,
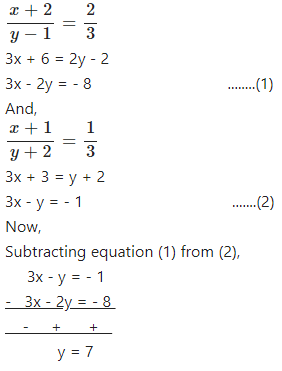
From (1) ,
3x – 2 (7) = – 8
3x = – 8 + 14
x = 2
Required fraction = 2/7
Question 9
The sum of the numerator and the denominator of a fraction is equal to 7. Four times the numerator is 8 less than 5 times the denominator. Find the fraction.
Answer
Let the numerator and denominator of a fraction be x and y respectively .Then the fraction will be .
According to the question,
x + y = 7 …(1)
5y – 4x = 8 …(2)
Multiplying equation no. (1) by 4
4x + 4y = 28 …(3)
Adding equation (3) and (2)
4x + 4y = 28
+ – 4x + 5y = 8
9y = 36
y = 4
From (1),
x + 4 = 7
x = 3
Required fraction =
Question 10
lf the numerator of a fraction is multiplied by 2 and its denominator is increased by 1, it becomes 1. However,if the numerator is increased bu 4 and denominator is multiplied by 2, the fraction becomes . Find the fraction.
Answer
Let the numerator of the fraction be x and the denominator be y.
So, the Fraction is
According to the question,
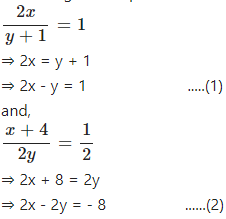
Solving equations (1) and (2), We get
y = 9
Putting the value of y in (1), we get
2x – 9 = 1
⇒ 2x = 1 + 9
⇒ x = 5
So, the fraction is 5/9
Question 11
A Fraction becomes if 5 subtracted from its numerator and 3 is subtracted from its denominator. If the denominator of this fraction is 5 more than its numerator. Find the fraction.
Answer
Let the numerator of the fraction be x and denominator of the fraction be y.
Then, the fraction =
According to given condition, we have

⇒ 2x – 10 = y – 3
⇒ 2x – y = 7 …(1)
And,
x + 5 = y
⇒ x – y = – 5 …(2)
Subtracting (2) from (1), We get
x = 12
⇒ y = x + 5
⇒ y = 12 + 5 = 17
Hence, the fraction is .
Question 12
The sum of the digits of the digits of two digit number is 5. If the digits are reversed, the number is reduced by 27. Find the number.
Answer
Let the digit at unit’s place be x and the digit at ten’s place y.
Required no. = 10y + x
If the digit’s are reversed,
Reversed no. = 10y + x
According to the question,
x + y = 5 …(1)
and,
(10y + x) – (10x + y) = 27
9y – 9x = 27
y – x = 3 …(2)
Now,
Adding equation (1) and (2),
y – x = 3 ….(2)
+ y + x = 5 ….(1)
2y = 8
y = 4
From (1)
x + 4 = 5
x = 1
Require no is
10 (4) + 1 = 41
Question 13
The sum of the digits of a two digit number is 7. If the digits are reversed, the new number decreased by 2, equals twice the original number. Find the number.
Answer
Let the digit at unit’s place be x and the digit at ten’s place be y.
Required no. = 10y + x
If the digit’s are reversed
Reversed no. = 10x + y
According to the question,
x + y = 7 …(1)
and,
10x + y – 2 = 2(10y + x).
8x – 19y = 2 …(2)
Multiplying equation no. (1) by 19.
19x + 19y = 133 …(3)
Now adding equation(2) and (3)
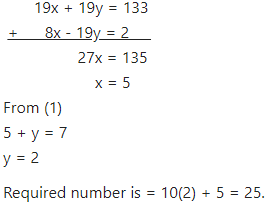
Question 14
The ten’s digit of a two digit number is three times the unit digit. The sum of the number and the unit digit is 32. Find the number.
Answer
Let the digit at unit’s place be x and the digit at ten’s place be y.
Required no. = 10y + x
According to the question,
y = 3x
⇒ 3x – y = 0 …(1)
and,
10y + x + x = 32
10y + 2x = 32 …(2)
Multiplying equation no. (1) by 10.
30x – 10y = 0 ….(3)
Now,
Adding equation (3) and (2)

Question 15
A two-digit number is such that the ten’s digit exceeds twice the unit’s digit by 2 and the number obtained by inter-changing the digits is 5 more than the the sum of the digits. Find the two digit number.
Answer
Let the digit a unit’s place be x and the digit at ten’s place be y.
Required no. = 10y + x.
According to the question,
y – 2x = 2
-2x + y = 2 …(1)
and,
(10x + y) -3 (y + x) = 5
7x – 2y = 5 …(2)
Multiplying equation no. (1) by 2.
– 4x + 2y = 4 …(3)
Now adding (2) and (3),
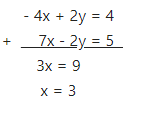
From (1) ,we get
-2(3) + y = 2
y = 8
Required number is 10(8) + 3 = 83
Question 16
Four times a certain two digit number is seven times the number obtained on interchanging its digits. If the difference between the digits is 4; find the number.
Answer
Let x be the number at the ten’s place.
and y be the number at the unit’s place.
So, the number is 10x + y.
Four times a certain two-digit number is seven times
the number obtained on interchanging its digits.
⇒ 4( 10x + y ) = 7( 10y + x )
⇒ 40x + 4y = 70y + 7x
⇒ 33x – 66y = 0
⇒ x – 2y = 0 ….(1)
If the difference between the digits is 4, then
⇒ x – y = 4 …(2)
Subtracting equation (1) from equation (2), we get :
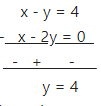
Subtracting y = 4 in equation (1), We get
x – 2(4) = 0
⇒ x = 8
∴ The number is 10x + y = 10(8) + 4 = 84.
Question 17
The sum of two digit number and the number obtained by interchanging the digits of the number is 121. If the digits of the number differ by 3, find the number.
Answer
Let the tens digit of the number be x and the units digit be y.
So, the number is 10x + y.
The number obtained by interchanging the digits will be 10y + x.
According to question, we have
10x + y + 10y + x = 121
⇒ 11x + 11y = 121
⇒ 11( x + y ) = 121
⇒ x + y = 11 …(1)
And,
x – y = 3 …(2)
Adding (1) and (2), We get
∴ 2x = 14
x = 7
∴ y = 11 – x = 11 – 7 = 4
Hence, the number is 74.
A two digit number is obtained by multiplying the sum of the digits by 8. Also, it is obtained by multiplying the difference of the digits by 14 and adding 2. Find the number.
Answer
Let the tens digit of the number be x and the units digit be y.
So, the number is 10x + y.
According to the question,
10x + y = 8( x + y )
⇒ 10x + y = 8x + 8y
⇒ 2x = 7y ….(1)
and 10x + y = 14( x – y ) + 2 or 10x + y = 14( y – x ) + 2
⇒ 4x – 15y = – 2 …(2) or 24x – 13y = 2 ….(3)
Solving (1) and (2), We get
y = 2 and x = 7
Solving (1) and (3), We get
y =
This is not possible, since y is a digit and cannot be in fraction form.
So, the number is 72.
Concise Selina Publisher’s ICSE Class-9 Maths Solved Questions of Exercise – 6(F) Simultaneous Linear Equations
Question 1
Five years ago, A’s age was four times the age of B. Five years hence, A’s age will be twice the age of B. Find their preset ages.
Answer
Let present age of A = x years
And present age of B = y years
According to the question,
Five years ago,
x – 5 = 4(y – 5)
x – 4y = -15 …(1)
Five years later,
x + 5 = 2(y + 5)
x + 5 = 2y + 10
x – 2y = 5 ….(2)
Now subtracting (1) from (2)
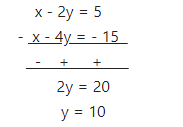
From (1)
x – 4 (10) = -15
x = 25
Present ages of A and B are 25 years and 10 years respectively.
Question 2
A is 20 years older than B. 5 years ago, A was 3 times as old as B. Find their present ages.
Answer
Let A’s presentage be x years
and B’s present age be y years
According to the question
x = y + 20
x – y = 20 …(1)
Five years ago,
x – 5 = 3(y – 5)
x – 5 = 3y – 15
x – 3y = – 10 …(2)
Subtracting (1) and (2),
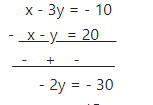
y = 15
From (1)
x = 15 + 20
x = 35
Thus, present ages of A and B are 35 years and 15 years.
Question 3
Four years ago, a mother was four times as old as her daughter. Six years later, the mother will be two and a half times as old as her daughter at that time. Find the present ages of mother and her daughter.
Answer
Let the present age of the mother be x years.
and the present age of the daughter be y year.
According to the queation,
x – 4 = 4( y – 4 )
⇒ x – 4 = 4y – 16
⇒ x – 4y = – 12 …(1)
And,
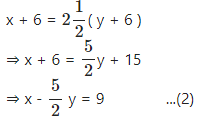
solving (1) and (2), We get
y = 14 and x = 44
Hence, the present age of the mother is 44 years
and the present age of the daughter is 14 years.
Question 4
The age of a man is twice the sum of the ages of his two children. After 20 years, his age will be equal to the sum of the ages of his children at that time. Find the present age of the man.
Answer
Let the present age of the man be x years.
and let the sum of the ages of his two children be y years.
According to the question,
x = 2y …(1)
and x + 20 = y + 40 ….(2) [ Since he has two children ]
Solving (1) and (2), We get,
2y + 20 = y + 40
⇒ y = 20
So, x = 2y ⇒ x = 40.
Hence, the present age of the man is 40 years.
Question 5
The annual incomes of A and B are in the ratio 3 : 4 and their annual expenditure are in the ratio 5 : 7. If each Rs. 5000; find their annual incomes.
Answer
Let A’s annual in come = Rs.x
and B’s annual income = Rs. y
According to the question,

From (1)
4x – 3(40,000) = 0
x = 30,000
Thus, A’s income in Rs. 30,000 and B’s income is Rs. 40,000.
Question 6
In an examination, the ratio of passes to failures was 4 : 1. Had 30 less appeared and 20 less passed, the ratio of passes to failures would have been 5 : 1. Find the number of students who appeared for the examination.
Answer
Let the no. of pass candidates be x
and the no. of fail candidates be y.
According to the question,
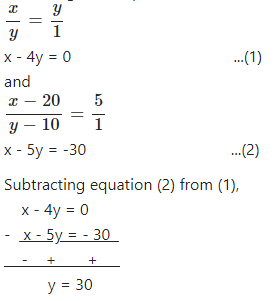
From (1)
– 4(30) = 0
x = 120
Total students appeared = x + y = 120 + 30 = 150.
Question 7
A and B both the have some pencils. If A gives 10 pencils to B, then B will have twice as many as A. And if B gives 10 pencils to A, then they will have the same number of pencils. How many pencils does each have ?
Answer
Let the numberof pencils with A = x
and the number of pencils with B = y.
If A gives 10 pencils to B,
y + 10 = 2( x – 10 )
2x – y = 30 …(1)
If B gives to pencils to A
y – 10 = x + 10
x – y = – 20 …(2)
Subtracting equation (1) and (2)

From (1)
2(50) – y = 30
y = 70
Thus, A has 50 pencils and B has 70 pencils.
Question 8
1250 persons went to sea a circus-show. Each adult paid Rs. 75 and each child paid Rs. 25 for the admission ticket. Find the number of adults and number of children, if the total collection from them amounts to Rs. 61,250.
Answer
Let the number of adults = x
and the number of children = y
According to the question,
x + y = 1250 …(1)
75x + 25y = 61250 …(2)
Subtracting equation (2) from (1)
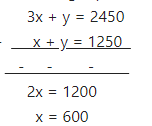
From (1)
600 + y = 1250
y = 650
Thus, number of adults = 600 and the number of children = 650.
Question 9
Two articles A and B are sold for Rs. 1,167 making 5% profit on A and 7% profiton A and 7% profit on B. IF the two articles are sold for Rs. 1,165, a profit of 7% is made on A and a profit of 5% is made on B. Find the cost prices of each article.
Answer
Let the cost price of article A = Rs. x
and the cost price of articles B = Rs. y
According to the question,
( x + 5% of x ) +( y + 7% of y ) = 1167

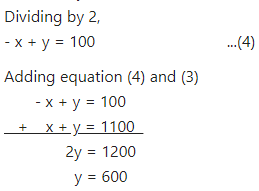
from (3)
x +600 = 1100
x = 500
Thus, cost price of article A is Rs. 500 and that of article B is Rs. 600.
Question 10
Pooja and Ritu can do a piece of work in 120/7 days. If one day work of Pooja be three fourth of one day work of Ritu’ find in how many days each will do the work alone.
Answer
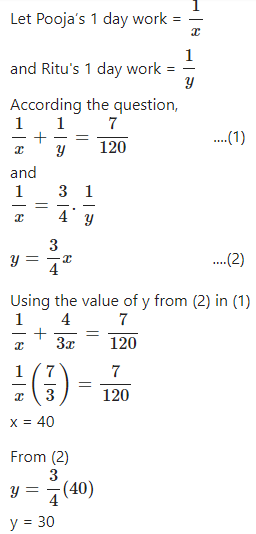
Pooja will complete the work in 40 days and Ritu will complete the work in 30 days.
Exercise – 6(G) Simultaneous Linear Equations (Including Problems) Class-9th Concise Selina ICSE Maths Solutions
Question 1
Rohit says to Ajay, “Give me hundred, I shall then become twice as rich as you.” Ajay replies, “if you give me ten, I shall be six times as rich as you.” How much does each have originally ?
Answer
Let Rohit has Rs. x and Ajay has Rs. y
When Ajay gives Rs. 100 to Rohit
x + 100 = 2(y – 100)
x – 2y = -300 …(1)
When Rohit gives Rs. 10 to Ajay
6(x-10) = y + 10
6x – y = 70 …(2)
Multiplying equation no. (2) By 2.
12x – 2y = 140 …(3)
Subtracting equation (1) and (3)
12x – 2y = 140
– x – 2y = – 300
– + +
11x = 440
x = 40
From (1)
40 – 2y = – 300
⇒ – 2y = – 340
⇒ y = 170
Thus, Rohit has Rs. 40 and Ajay has Rs. 170.
Question 2
The sum of a two digit number and the number obtained by reversing the order of the digits is 99. Find the number, if the digits differ by 3.
Answer
Let the digits in the tens place be x and the digit in the units place be y.
∴ Number = 10x + y
Number on reversing the digits = 10y + x
The difference between the digits = x – y or y – x
Given : ( 10x + y ) + ( 10y + x ) = 99
⇒ 11x + 11y = 99
⇒ x + y = 9 …(1)
x – y = 3 …(2)
or y – x = 3 …(3)
On solving equations (1) and (2), We get
2x = 12 ⇒ x = 6
So, y = 3
On solving equation (1) and (3), We get
2y = 12 ⇒ y = 6
So, x = 3
Number = 10x + y = 10(6) + 3 = 63
or Number = 10x + y = 10(3) + 6 = 36
∴ Required number = 63 or 36.
Question 3
Seven times a two digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3 find the number.
Answer
Let the digit at ten’s place be x And the digit at unit’s place be y.
Required number = 10x + y
When the digits are interchanged,
Reversed number = 10y + x
According to the question,
7(10x + y) = 4(10y + x)
∴ 70x + 7y = 40y + 4x
∴ 66x = 33y
∴ 2x – y = 0 …(1)
The difference between the digits is 3.
y – x = 3 …(2)
Adding equation (1) and (2)
y – x = 3
+ – y + 2x = 0
x = 3
From (1)
2(3) – y = 0
y = 6
Thus, Required number = 10(3) + 6 = 36
Question 4
From Delhi station, if we buy 2 tickets for station A and 3 tickets for station B, the total cost is Rs. 77. But if we buy 3 tickets for station A and 5 tickets for station B, the total cost is Rs. 124. What are the fares from Delhi to station A and to station B ?
Answer
Let, the fare of ticket for station A be Rs. x and the fare of ticket for station B be Rs. y
According, to the question
2x + 3y = 77 …(1) and
3x + 5y = 124 …(2)
Multiplying equation no. (1) by 3 and (2) by 2.
6x + 9y = 231 …(3)
6x + 10y = 248 ….(4)
Subtracting equation (4) from (3)
6x + 9y = 231
– 6x + 10y = 248
– – –
– y = – 17
y = 17
From (1)
2x + 3 (17) = 77
2x = 77 – 51
2x = 26
x = 13
Thus, fare for station A = Rs. 13 and, fare for station B = Rs. 17.
Question 5
The sum of digit of a two digit number is 11. If the digit at ten’s place is increased by 5 and the digit at unit place is decreased by 5, the digits of the number are found to be reversed. Find the original number.
Answer
Let x be the number at the ten’s place.
and y be the number at the unit’s place.
So, the number is 10x + y.
The sum of digit of a two digit number is 11.
⇒ x + y = 11 …(1)
lf the digit at ten’s place is ineased by 5 and the digit at unit place is decreased by 5,
the digits of the number are found to be reversed.
⇒ 10( x + 5 ) + ( y – 5 ) = 10y + x
⇒ 9x – 9y = -45
⇒ x – y = -5 …(2)
Subtracting equation (1) from equation (2), we get :
x – y = – 5
– x + y = 11
– – –
– 2y = – 16
⇒ y = 8
Substituting y = 8 in equation (1), we get
x + 8 = 11
⇒ x = 3
∴ The number is 10x + y = 10(3) + 8 = 38.
Question 6
90% acid solution (90% pure acid and 10% water) and 97% acid solution are mixed to obtain 21 litres of 95% acid solution. How many litres of each solution are mixed.
Answer
Let the quantity of 90% acid solution be x litres and The quantity of 97% acid solution be y litres
According to the question,
x + y = 21 …(1)
and 90% of x + 97% of y = 95% of 21
90x + 97y = 1995 …(2)
Multiplying equation no. (1) by 90, we get,
90x + 90y = 1890 ….(3)
Subtracting equation (2) from (3)
90x + 90y = 1890
– 90x + 97y = 1995
– – –
– 7y = – 105
y = 15
From (1)
x + 15 = 21
x = 6
Hence, 90% acid solution is 6 litres and 97% acid solution is 15 litres.
Question 7
The class XI students of school wanted to give a farewell party to the outgoing students of class XII. They decided to purchase two kinds of sweets, one costing Rs. 250 per kg and other costing Rs. 350 per kg. They estimated that 40 kg of sweets were needed. If the total budget for the sweets was Rs. 11,800; find how much sweets of each kind were bought ?
Answer
Assume x kg of the first kind costing Rs. 250 per kg and y kg of the second kind costing Rs. 350 per kg sweets were bought.
It is estimated that 40 kg of sweets were needed.
⇒ x + y = 40 ….(1)
The total budget for the sweets was Rs. 11,800.
⇒ 250x + 350y = 11,800 ….(2)
Multiply equation (1) by 250, We get :
250x + 250y = 10,000 …..(3)
Subtracting equation (2) from (3),
250x + 250y = 10,000
– 250x + 350y = 11,800
– – –
– 100y = – 1800
y = 18
Substituting y = 18 in equation (1), We get
x + 18 = 40
⇒ x = 22
∴ 22 kgs of the first kind costing Rs. 250 per kg and 18 kgs of the second kind costing Rs. 350 per kg sweets were bought.
Question 8
Mr. and Mrs. Abuja weight x kg and y kg respectively. They both take a dieting course, at the end of which Mr. Ahuja loses 5 kg and weights as much as his wife weighed before the course. Mrs. Ahuja loses 4 kg and weighs 78th of what her husband weighed before the course. Form two equations in x and y, find their weights before taking the dieting course.
Answer
Weight of Mr. Ahuja = x kg and weight of Mrs. Ahuja = y kg.
After the dieting,
x – 5 = y
x – y = 5 …(1)
and,
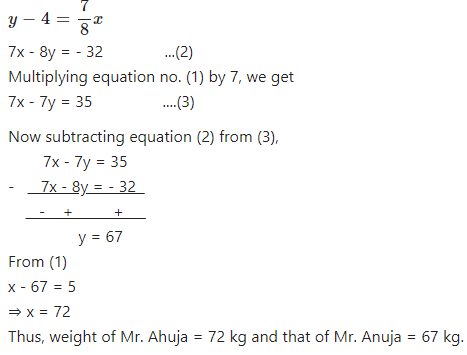
Question 9
A part of monthly expenses of a family is constants and the remaining vary with the number of members in the family. For a family of 4 person, the total monthly expenses are Rs. 10,400 whereas for a family of 7 persons, the total monthly expenses are Rs. 15,800. Find the constant expenses per month and the monthly expenses of each member of a family.
Answer
Let x be the constant expense per month of the family,
and y be the expense per month for a single member of the family,
For a family of 4 people,
the total monthly expense is Rs. 10,400.
x + 4y = 10,400 …(1)
For a family of 7 people,
the total monthly expense is Rs. 15,800.
x + 7y = 15,800 …(2)
Subtracting equation (1) from equation (2),We get :
x + 7y = 15800
– x + 4y = 10400
– – –
3y = 5400
y = 1800
Substituting y = 1800 in equation (1), We get
x + 4( 1800 ) = 10,400
⇒ x = 3200.
∴ The constant expense is Rs. 3,200 per month and the monthly expense of each member of a family is Rs.1,800.
The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is Rs. 315 and for a journey of 15 km, the charge paid is Rs. 465. What are the fixed charges and the charge per kilometer ? How much does a person have to pay for travelling a distance of 32 km ?
Answer
Let the fixed charge be Rs. x and the charge per kilometer be Rs. y.
The charges for 10 km = Rs. 10y
The charges for 15 km = Rs. 15y
According to the question,
x+ 10y = 315 …(1)
x+ 15y = 465 ….(2)
Solving the equations, we get
– 5y = – 150
⇒ y = 30
and x = 315 – 10y = 315 – 10(30) = 15
So, the fixed charges is Rs. 15 and the charges per kilometer is Rs. 30.
To travel 32 km, a personal has to pay
= Rs. 15 + Rs. 30( 32 ) = Rs. 15 + Rs. 960 = Rs. 975.
Question 11
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Geeta paid Rs. 27 for a book kept for seven days, while Mohit paid Rs. 21 for the book he kept for five days. Find the fixed charges and the charge for each extra day.
Answer
Let the fixed charges be Rs. x and the charge for each extra day be Rs. y.
According to the question,
x + 4y = 27 …(1)
and x + 2y = 21 ….(2)
Solving the equations, we get
2y = 6
∴ y = 3
and x = 21 – 2y = 21 – 2(3) = 15
Hence, the fixed charges is Rs. 15 and the charge for each extra day is Rs. 3.
Question 12
The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. However, if the length of this rectangle increases by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Answer
Let the length of the rectangle be x units and the breadth of the rectangle be y units.
We know that, area of a rectangle = length x breadth = xy
According to the question,
xy – 9 = ( x – 5 )( y + 3 )
⇒ xy – 9 = xy + 3x – 5y – 15
⇒ 3x – 5y = 6 ….(1)
xy + 67 = ( x + 3 )( y + 2 )
⇒ xy + 67 = xy + 2x + 3y + 6
⇒ 2x + 3y = 61 …(2)
Multiply (1) by 2 and (2) by 3, we get
6x – 10y = 12 …(3)
6x + 9y = 183 …(4)
Subtracting equation (4) from (3),
6x – 10y = 12
– 6x + 9y = 183
– – –
– 19y = – 171
y = 9
Putting y = 9 in equation (1)
3x – 5y = 6
3x – 5(9) = 6
3x = 6 + 45
x =
x = 17
Hence, the length of the rectangle is 17 units and the breadth of the rectangle is 9 units.
Question 13
It takes 12 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter is used for 9 hours, only half of the pool is filled. How long would each pipe take to fill the swimming pool ?
Answer
Let the pipe with larger diameter and smaller diameter be pipes A and B respectively.
Also, let pipe A work at a rate of x hours/ unit and pipe B work at a rate of Y hours / unit.
According to the question,
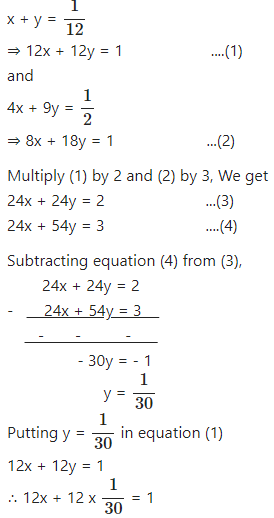
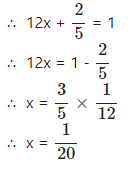
Hence, the pipe with larger diameter will take 20 hours to fill the swimming pool and the pipe with smaller diameter will take 30 hours to fill the swimming pool.
— End of Simultaneous Linear Equations Class-9 Concise Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -9
Thanks



