Special Types Quadrilaterals ICSE Class-8th Concise Selina

Special Types Quadrilaterals ICSE Class-8th Concise Selina Mathematics Solutions Chapter-17 . We provide step by step Solutions of Exercise / lesson-17 Special Types Quadrilaterals for ICSE Class-8 Concise Selina Mathematics. Our Solutions contain all type Questions of Exe-17 to develop skill and confidence . Visit official Website CISCE for detail information about ICSE Board Class-8 Mathematics.

Special Types Quadrilaterals ICSE Class-8th Concise Selina Mathematics Solutions Chapter-17

---

 Exercise – 17 

Question 1.

In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
Answer

AB = CD

5x – 7 = 3x + 1

⇒ 5x – 3x = 1+7

⇒ 2x = 8

⇒ x = 4

CD = 3 x 4+1 = 13

Hence 135°, 45°, 135° and 45° ; 13

Question 2.

In parallelogram PQRS, ∠Q = (4x – 5)° and ∠S = (3x + 10)°. Calculate : ∠Q and ∠R.
Answer

Question 3.

In rhombus ABCD ;
(i) if ∠A = 74° ; find ∠B and ∠C.
(ii) if AD = 7.5 cm ; find BC and CD.
Answer

Question 4.

In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QR = 9x – 8. Find QS
Answer

As diagonals of square are equal.

PR = QS

5x = 9x – 8

⇒ 5x – 9x = -8

⇒ -4x = -8

⇒ x = 2

QS = 9x – 8 = 9 x 2 – 8 =10

Question 5.

ABCD is a rectangle, if ∠BPC = 124°
Calculate : (i) ∠BAP (ii) ∠ADP

Answer

Diagonals of rectangle are equal and bisect each other.

∠PBC = ∠PCB = x (say)

But ∠BPC + ∠PBC + ∠PCB

= 180°

124° + x + x

= 180°

2x = 180° – 124°

2x = 56°

⇒ x = 28°

∠PBC = 28°

But ∠PBC = ∠ADP

[Alternate ∠s]

∠ADP = 28°

Again ∠APB = 180° – 124°

= 56°

Also PA = PB

∠BAP =1/2(180° – ∠APB)

= (1/2) x (180°- 56°)

= (1/2)×124° = 62°

Hence

(i) ∠BAP = 62° (

ii) ∠ADP =28°

Question 6.

ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.

Answer

ABCD is Rhombus (Given)

AB = BC

∠BAC = ∠ACB

(∠s opp. to equal sides)

But ∠BAC = 38° (Given)

∠ACB = 38°

In ∆ABC,

∠ABC + ∠BAC + ∠ACB

= 180°

∠ABC + 38°+ 38°

= 180°

∠ABC = 180° – 76°

= 104°

But ∠ABC = ∠ADC (opp. ∠s of rhombus)

∠ADC = 104°

∠DAC = ∠DCA ( AD = CD)

∠DAC = (1/2) [180° – 104°]

∠DAC = (1/2)× 76°

= 38°

Hence

(i) ∠ACB = 38°

(ii) ∠DAC = 38°

(iii) ∠ADC = 104° Ans.

Question 7.

ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.
Answer

Question 8.

PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
Answer

Given :

||gm PQRS in which diagonals PR & QS intersect at M.
∠PMS = 54° ; ∠QSR = 25° and ∠SQR=30°

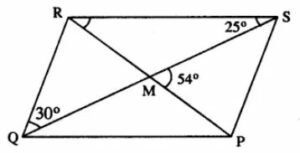
To find :

(i) ∠RPS

(ii) ∠PRS

(iii) ∠PSR

Proof :

QR || PS

⇒ ∠PSQ = ∠SQR (Alternate ∠s)

But ∠SQR = 30° (Given)

∠PSQ = 30°

In ∆SMP,

∠PMS + ∠ PSM +∠MPS

= 180° or 54° + 30° + ∠RPS

= 180°

∠RPS = 180°- 84°

= 96°

Now ∠PRS + ∠RSQ = ∠PMS

∠PRS + 25° =54°

∠PRS = 54° – 25°

= 29°

∠PSR = ∠PSQ + ∠RSQ = 30°+25°

= 55°

Hence

(i) ∠RPS = 96°

(ii) ∠PRS = 29°

(iii) ∠PSR = 55°

Question 9.

Given : Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove : M is mid-point of LN.
Answer

Question 10.

In an Isosceles-trapezium, show that the opposite angles are supplementary.
Answer

Question 11.

ABCD is a parallelogram. What kind of quadrilateral is it if :
(i) AC = BD and AC is perpendicular to BD?
(ii) AC is perpendicular to BD but is not equal to it?
(iii) AC = BD but AC is not perpendicular to BD?
Answer

Question 12.

Prove that the diagonals of a parallelogram bisect each other.
Answer

Question 13.

If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
Answer

Question 14.

In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
Answer

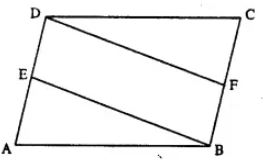
Given: 

Parallelogram ABCD in which E and F are mid-points of AD and BC respectively.

To Prove:

BFDE is a Parallelogram.

Proof:

E is the mid-point of AD. (Given)

DE =  AD

Also, F is mid-point of BC (Given)

BF =  BC

But AD = BC

(opp. sides of parallelogram)

BF = DE

Again AD || BC

=> DE || BF

Now DE || BF and DE

= BF

Hence BFDE is a parallelogram.

Question 15.

In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
Answer

DE bisects ∠ADC.

Now AD || BC

=> ∠D + ∠C = 180°

2∠6+2∠1 = 180°

DE and CE are bisectors.

∠6 + ∠1 = 180°/2

∠6 + ∠1 = 90°

But ∠DEC + ∠6 + ∠1 = 180°

∠DEC + 90° = 180°

∠DEC = 180° – 90°

∠DEC = 90°

Hence the result.

Question 16.

In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.

Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
Answer

Given:

In parallelogram ABCD bisector of angles P and Q, meet at A, bisectors of ∠R and ∠S meet at C. Forming a quadrilateral ABCD as shown in the figure.

To prove :
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 9°
(vi) ABCD is a rectangle

Proof :

In parallelogram PQRS,

PS || QR (opposite sides)

∠P +∠Q = 180°

and AP and AQ are the bisectors of consecutive angles

∠P and ∠Q of the parallelogram

∠APQ + ∠AQP = 12 x 180° = 90°

But in ∆APQ,

∠A + ∠APQ + ∠AQP = 180° (Angles of a triangle)

∠A + 90° = 180°

∠A = 180° – 90°

(i) ∠A = 90°

Similarly PQ || SR

∠PSB + SPB = 90°

(ii) and ∠PBS = 90°

But, ∠ABC = ∠PBS (Vertically opposite angles)

(iii) ∠ABC = 90°

Similarly we can prove that

(iv) ∠ADC = 90° and ∠C = 90°

(vi) ABCD is a rectangle (Each angle of a quadrilateral is 90°)

Hence proved.

Question 17.

In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
Answer

Given:

In parallelogram ABCD, X and Y are the mid-points of sides AB and DC respectively AY and CX are joined.

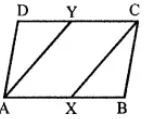
To prove :
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram

Proof:

AB || DC and X and Y are the mid-points of the sides AB and DC respectively

(i) AX = YC (of opposite sides of a parallelogram)

(ii) AX || YC

(iii) AXCY is a parallelogram (A pair of opposite sides are equal and parallel)

Hence proved.

Question 18.

The given figure shows a parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.

Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Answer

Given:

In parallelogram ABCD, points M and N lie on the diagonal BD such that DM = BN
AN, NC, CM and MA are joined

To prove :
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM = CN
(iii) ANCM is a parallelogram

Proofed :
(i) In ∆DMC and ∆BNA.

CD = AB

(opposite sides of ||gm ABCD)

DM = BN (given)

∠CDM = ∠ABN

(alternate angles)

∆DMC = ∆BNA

(SAS axiom)

CM =AN (c.p.c.t.)

Similarly, in ∆AMD and ∆CNB

AD = BC

(opposite sides of ||gm)

DM = BN (given)

∠ADM = ∠CBN – (alternate angles)

∆AMD = ∆CNB (SAS axiom)

AM = CN (c.p.c.t.)

(iii) CM = AN and AM = CN (proved)

ANCM is a parallelogram (opposite sides are equal)

Hence proved.

Question 19.

The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.

Answer

In rhombus ABCD, diagonals AC and BD bisect each other at 90°

∠BCD = 80°

Diagonals bisect the opposite angles also ∠BCD =

∠BAD (Opposite angles of rhombus)

∠BAD = 80° and ∠ABC = ∠ADC = 180° – 80° = 100°

Diagonals bisect opposite angles

∠OCB or ∠PCB = (80°/2) = 40°

In ∆PCM,

Ext. CPD = ∠OCB + ∠PMC

110° = 40° + x

⇒ x = 110° – 40° = 70°

and ∠ADO = 1/2 ∠ADC = (1/2)×100°=50°

Hence x = 70° and y = 50°

Question 20.

Use the information given in the alongside diagram to find the value of x, y and z.

Answer

ABCD is a parallelogram and AC is its diagonal which bisects the opposite angle

Opposite sides of a parallelogram are equal

3x + 14 = 2x + 25

⇒ 3x – 2x = 25 – 14

⇒ x = 11

∴ x = 11 cm

∠DCA = ∠CAB (Alternate angles)

y + 9° = 24

y = 24° – 9° = 15°

∠DAB = 3y° + 5° + 24° = 3 x 15 + 5 + 24° = 50° + 24° = 74°

∠ABC =180°- ∠DAB = 180° – 74° = 106°

z = 106°

Hence x = 11 cm, y = 15°, 

z = 106°

Question 21.

The following figure is a rectangle in which x : y = 3 : 7; find the values of x and y.

Answer

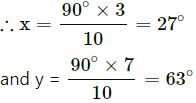
Question 22.

In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:

(i) ∠EAC = ∠ACB
(ii) ABCE is a parallelogram.
Answer

ABCE is a quadrilateral in which AC is its diagonal and

AB || EC, AB = AC

BA is produced to D

AE bisects ∠DAC

To prove:

(i) ∠EAC = ∠ACB

(ii) ABCE is a parallelogram

Proof:

(i) In ∆ABC and ∆ZAEC

AC=AC (common)

AB = CE (given)

∠BAC = ∠ACE (Alternate angle)

∆ABC = ∆AEC (SAS Axiom)

(ii) ∠BCA = ∠CAE (c.p.c.t.)

But these are alternate angles

AE || BC

But AB || EC (given)

Hence –

so  ABCD is a parallelogram

 

— End of Special Types Quadrilaterals Solutions :–

 

Return to – Concise Selina Maths Solutions for ICSE Class -8 

---