Substitution ICSE Class-6th Concise Mathematics Selina Solutions Chapter-20 (Including Use of Brackets as Grouping Symbols). We provide step by step Solutions of Exercise / lesson-20 Substitution (Including Use of Brackets as Grouping Symbols) for ICSE Class-6 Concise Selina Mathematics. Our Solutions contain all type Questions of Exe-20 A, Exe-20 B, Exe-20 C and Revision Exercise to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6 .
Substitution ICSE Class-6th Concise Mathematics Selina Solutions Chapter-20 (Including Use of Brackets as Grouping Symbols)
–: Select Topics :–
Exercise – 20 A Substitution (Including Use of Brackets as Grouping Symbols) for ICSE Class-6th Concise Selina Maths
Question- 1.
Fill in the following blanks, when :
x = 3,y = 6, z = 18, a = 2, b = 8, c = 32 and d = 0.


Answer-1
(i ) x + y = 3 + 6 = 9
(ii) y − x = 6 − 3 = 3
(iii) y/ x= 6/3 = 2
(iv) c ÷ b = c/b =32 / 8 = 4
(v) z ÷ x = z/x = 18/ 3 = 6
(vi) y × d = 6 × 0 = 0
(vii) d ÷ x = d/x = 0/3 = 0
(viii) ab + y = 2 × 8 + 6 = 16 + 6 = 22
(ix) a + b + x = 2 + 8 + 3 = 13
(x) b + z − d = 8 + 18 − 0 = 26
(xi) a − b + y = 2 − 8 + 6 = 8 − 8 = 0
(xii) z − a − b = 18 − 2 − 8 = 18 − 10 = 8
(xiii) d − a + x = 0 − 2 + 3 = 1
(xiv) xy − bd = 3 × 6 − 8 × 0 = 18 − 0 = 18
(xv) xz + cd = 3 × 18 + 32 × 0 = 54 + 0 = 54
Question -2.
Find the value of :

Answer-2
(i) p + 2q + 3r
= 1 + 2 × 5 + 3 × 2
= 1 + 10 + 6
= 17
(ii)
2a + 4b + 5c
= 2 × 5 + 4 × 10 + 5 × 20
= 10 + 40 + 100
= 150
(iii)
3a − 2b
= 3 × 8 − 2 × 10
= 24 − 20
= 4
(iv)
5x + 3y − 6z
= 5 × 3 + 3 × 5 − 6 × 4
= 15 + 15 − 24
= 30 − 24
= 6
(v)
2p − 3q + 4r −8s
= 2 × 10 − 3 × 8 + 4 × 6 − 8 × 2
= 20 − 24 + 24 − 16
= 20 − 16
= 4
(vi)
6m − 2n − 5p − 3q
= 6 × 20 − 2 × 10 − 5 × 2 − 3 × 9
= 120 − 20 − 10 − 27
= 120 − 57
= 63
Question -3.
Find the value of :

Answer-3
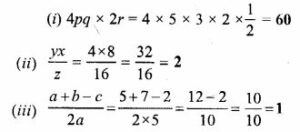
Question -4.
If a = 3, b = 0, c = 2 and d = 1, find the value of :

Answer-4
(i)
3a + 2b − 6c + 4d
= 3 × 3 + 2 × 0 − 6 × 2 + 4 × 1
= 9 + 0 − 12 + 4
= 13 − 12
= 1
(ii)
6a − 3b − 4c − 2d
= 6 × 3 − 3 × 0 − 4 × 2 − 2 × 1
= 18 − 0 − 8 − 2
= 18 − 10
= 8
(iii)
ab − bc + cd − da
= 3 × 0 − 0 × 2 + 2 × 1 − 1 × 3
= 0 + 0 + 2 − 3
= − 1
(iv)
abc − bcd + cda
= 3 × 0 × 2 − 0 × 2 × 1 + 2 × 1 × 3
= 0 − 0 + 6
= 6
(v)
a2 + 2b2 − 3c2
= 32 + 2 × 02 − 3 × 22
= 9 + 0 − 3 × 4
= 9 − 12
= − 3
(vi)
a2 + b2 − c2 + d2
= (3)2 + (0)2 − (2)2 + (1)2
= 9 + 0 − 4 + 1
= 6
(vii)
2a2 − 3b2 + 4c2 − 5d2
= 2 (3)2 − 3 (0)2 + 4 (2)2 − 5 (1)2
= 2 × 9 − 0 + 4 × 4 − 5 × 1
= 18 − 0 + 16 − 5
= 34 − 5
= 29
Question- 5.
Find the value of 5x2 – 3x + 2, when x = 2.
Answer-5
5x2 – 3x + 2
= 5(2)2 − 3(2) + 2
= 5(4) − 6 + 2
= 20 + 2 − 6
= 16
Question -6.
Find the value of 3x3 – 4x2 + 5x – 6, when x = -1.
Answer-6
3x3 – 4x2 + 5x – 6
= 3(− 1)3 − 4(− 1)2 + 5(− 1) − 6
= 3 × − 1 − 4 × 1 − 5 − 6
= − 3 − 4 − 5 − 6
= − 18
Question -7.
Show that the value of x3 – 8x2 + 12x – 5 is zero, when x = 1.
Answer-7
x3 – 8x2 + 12x – 5
= (1)3 − 8(1)2 + 12(1) − 5
= 1 − 8 + 12 − 5
= 13 − 13
= 0
Hence proved.
Question- 8.
State true and false :
(i) The value of x + 5 = 6, when x = 1
(ii) The value of 2x – 3 = 1, when x = 0
(iii) = -1,when x = 1
Answer-8
(i) True.
Verification x + 5 = 6,
When x = 1, 1 + 5 = 6
6 = 6
Hence proved
(ii) False.
Verification 2x − 3 = 1,
When x = 0
2 × 0 − 3 = 1
= 0 − 3
= − 3
−3 = 1
(iii) True.
Verification (2x-4 )/(x+1) = − 1,
When x = 1 = (2×1-4)/( 1+1 ) = − 1
= (2-4) / 2 =- 1= -2/2=-1
= − 1
Question- 9.
If x = 2, y = 5 and z = 4, find the value of each of the following :

Answer-9
(i)
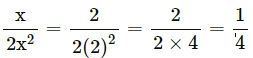
(ii)
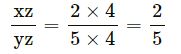

= (2)2−1 × (5)2 × (4)2−1
= 2 × 5 × 5 × 4
= 200
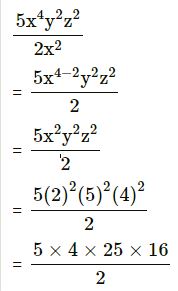
= 5 × 2 × 25 × 16
= 4,000
(vii)
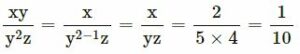
(viii)
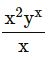
= x2−1yx
= xyx
= (2) (5)2
= 2 × 25
= 50
Question- 10.
If a = 3, find the values of a2 and 2a.
Answer-10
a2 = (3)2 = 3 × 3 = 9
2a = (2)3 = 2 × 2 × 2 = 8
Question -11.
If m = 2, find the difference between the values of 4m3 and 3m4.
Answer-11
4m3 = 4 (2)3 = 4 × 2 × 2 × 2 = 32
3m4 = 3 (2)4 = 3 × 2 × 2 × 2 × 2 = 48
Now, a difference 3m4 – 4m3 = 48 – 32 = 16
Substitution (Including Use of Brackets as Grouping Symbols) ICSE Class-6th Concise Mathematics Selina Solutions Exercise – 20 B
Question-1
Evaluate :
(i) (23 – 15) + 4
(ii) 5x + (3x + 7x)
(iii) 6m – (4m – m)
(iv) (9a – 3a) + 4a
(v) 35b – (16b + 9b)
(vi) (3y + 8y) – 5y
Answer-1
(i) (23 – 15) + 4 = 8 + 4 = 12
(ii) 5x + (3x + 7x) = 5x + 10x = 15x
(iii) 6m – (4m – m) = 6m – 3m = 3m
(iv) (9a – 3a) + 4a = 6a + 4a = 10a
(v) 35b – (16b + 9b) = 35b – 25b = 10b
(vi) (3y + 8y) – 5y = 11y – 5y = 6y
Question- 2.
Simplify :


Answer-2
(i) 12x − (5x + 2x)
= 12x − 7x = 5x
(ii) 10m + (4n − 3n) − 5n
= 10m + n − 5n
= 10m − 4n
(iii) (15b − 6b) − (8b + 4b)
= 9b − 12b
= − 3b
(iv) − (− 4a − 8a)
= − (− 12a)
= 12a
(v) x − (x − y) − (− x + y)
= x − x + x + y − y
= x
(vi) p + (− q − r − s) − (p − q − r)
= p − q − r − s − p + q + r
= p − p − q + q − r + r − s
= − s
(vii) (a + b) − (c + d) − (e − f)
= a + b − c − d − e + f
(viii) 3x + (8x − 5x) − (7x − x)
= 3x + 3x − 6x
= 6x − 6x
= 0
(ix) a − (a − b − c)
= a − a + b + c
= b + c
(x) 6a2 + (2a2 − a2) − (a2 − b2)
= 6a2 + a2 − a2 + b2
= 6a2 + b2
(xi) 2m − (3m + 2n − 6n)
= 2m − 3m − 2n + 6n
= − m + 4n
= 4n − m
(xii) − m − n − (− m) − m
= − m − n + m − m
= − m − n
(xiii) x + y − (x + y-x¯)
= x + y − (x + y − x)
= x + y − x − y + x
= x − x + x + y − y
= x
(xiv) 25y − (5x − 10y + 6x − 3y)
= 25y − 5x + 10y − 6x + 3y
= 25y + 10y + 3y − 5x − 6x
= 38y − 11x
(xv)
![]()
= 3x + (2x − x − 2)
= 3x + 2x − x − 2
= 4x − 2
(xvi)
![]()
= a − (2a − 4a − 3a)
= a − 2a + 4a + 3a
= 8a − 2a
= 6a
(xvii)
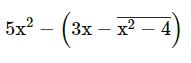
= 5x2 − (3x − x2 + 4)
= 5x2 − 3x + x2 − 4
= 5x2 + x2 − 3x − 4
= 6x2 − 3x − 4
(xviii)
![]()
= − (y − x) − (x + y − 2x − y)
= − y + x − x − y + 2x + y
= x − x + 2x − y − y + y
= 2x − y
Question -3.
Simplify :

Answer-3
(i) x − (y − z) + x + (y − z) + y − (z + x)
= x − y + z + x + y − z + y − z − x
= x + x − x − y + y + y + z − z − z
= x + y − z
(ii) x − [y + {x − (y + x)}]
= x − [y + {x − y − x}]
= x − [y + x − y − x]
= x − y − x + y + x
= x − x + x − y + y
= x
(iii) 4x + 3 (2x − 5y)
= 4x + 6x − 15y
= 10x − 15y
(iv) 2 (3a − b) − 5 (a − 3b)
= 6a − 2b − 5b + 15b
= 6a − 5a + 15b − 2b
= a + 13b
(v)
![]()
= p + 2 (q − r − p)
= p + 2q − 2r − 2p
= 2q − 2r − p
(vi)![]()
= a − [− {− (a − b + c)}]
= a − [− {− a + b − c}]
= a − [+ a − b + c]
= a − a + b − c
= b − c
(vii) 3x − [5y − {6y + 2 (10y − x)}]
= 3x − [5y − {6y + 20y − 2x}]
= 3x − [5y − 6y − 20y + 2x]
= 3x − 5y + 6y + 20y − 2x
= 3x − 2x + 6y + 20y − 5y
= x + 21y
(viii)![]()
= 5 {a2 − a (a − a + 2)}
= 5 {a2 − a2 + a2 − 2a}
= 5a2 − 5a2 + 5a2 − 10a
= 5a2 − 10a
Substitution (Including Use of Brackets as Grouping Symbols) Exercise – 20 C
ICSE Class-6th Concise Mathematics Selina Solutions
Question-1
Fill in the blanks :

Answer-1
(i) 2a + b − c = 2a + (b − c)
(ii) 3x − z + y = 3x − (z − y)
(iii) 6p − 5x + q = 6p − (5x − q)
(iv) a + b − c + d = a + (b − c + d)
(v) 5a + 4b + 4x − 2c = 4x − (2c − 5a − 4b)
(vi) 7x + 2z + 4y − 3 = − 3 + 4y + (7x + 2z)
(vii) 3m − 2n + 6 = 6 − (2n − 3m)
(viii) 2t + r − p − q + s = 2t + r − (p + q − s)
Question- 2.
Insert the bracket as indicated :

Answer-2
(i) x − 2y = − (2y − x)
(ii) m + n − p = − (p − m − n)
(iii) a + 4b − 4c = a + (4b − 4c)
(iv) a − 3b + 5c = a − (3b − 5c)
(v) x2 − y2 + z2 = x2 − (y2 − z2)
(vi) m2 + x2 − p2 = − (p2 − m2 − x2)
(vii) 2x − y + 2z = 2z − (y − 2x)
(viii) ab + 2bc − 3ac = 2bc − (3ac − ab)
Revision Exercise of Substitution
(Including Use of Brackets as Grouping Symbols)
ICSE Class-6th Concise Selina Solutions Chapter-20
Question-1
Find the value of 3ab + 10bc – 2abc when a = 2, b = 5 and c = 8.
Answer-1
a = 2, b = 5, c = 8
∴ 3ab + 10bc − 2abc
= 3 × 2 × 5 + 10 × 5 × 8 − 2 × 2 × 5 × 8
= 30 + 400 − 160
= 430 − 160
= 270
Question -2.
If x = 2, y = 3 and z = 4, find the value of 3x2 – 4y2 + 2z2.
Answer-2
x = 2, y = 3, z = 4
∴ 3x2 − 4y2 + 2z2
= 3 (2)2 − 4 (3)2 + 2 (4)2
= 3 × 4 − 4 × 9 + 2 × 16
= 12 − 36 + 32
= 12 + 23 − 36
= 44 − 36
= 8
Question- 3. Substitution ICSE Class-6th Concise
If x = 3, y = 2 and z = 1; find the value of:
(i) xy
(ii) yx
(iii) 3x2 – 5y2
(iv) 2x – 3y + 4z + 5
(v) y2 – x2 + 6z2
(vi) xy + y2z – 4zx
Answer-3
(i) x = 3, y = 2, z = 1
xy = 32 = 3 × 3 = 9
(ii) x = 3, y = 2, z = 1
yx = 23 = 2 × 2 × 2 = 8
(iii) x = 3, y = 2, z = 1
3x2 − 5y2 = 3(3)2 − 5(2)2
= 3 × 9 − 5 × 4
= 27 − 20
= 7
(iv) x = 3, y = 2, z = 1
2x – 3y + 4z + 5
= 2 × 3 − 3 × 2 + 4 × 1 + 5
= 6 − 6 + 4 + 5
= 15 − 6
= 9
(v) x = 3, y = 2, z = 1
y2 – x2 + 6z2
= (2)2 − (3)2 + 6(1)2
= 4 – 9 + 6 × 1
= 4 – 9 + 6
= 10 – 9
= 1
(vi) x = 3, y = 2, z = 1
xy + y2z – 4zx
= 3 × 2 + (2)2 × 1 − 4 × 1 × 3
= 6 + 4 − 12
= 10 − 12
= − 2
Question- 4.
If P = -12x2 – 10xy + 5y2, Q = 7x2 + 6xy + 2y2, and R = 5x2 + 2xy + 4y2 ; find :
(i) P – Q
(ii) Q + P
(iii) P – Q + R
(iv) P + Q + R
Answer-4
(i) P − Q
= (− 12x2 − 10xy + 5y2) − (7x2 + 6xy + 2y2)
= − 12x2 − 10xy + 5y2 − 7x2 − 6xy − 2y2
= − 12x2 − 7x2 − 10xy − 6xy + 5y2 − 2y2
= − 19x2 − 16xy + 3y2
(ii) Q + P
= (7x2 + 6xy + 2y2) + (– 12x2 – 10xy + 5y2)
= 7x2 + 6xy + 2y2 – 12x2 – 10xy + 5y2
= 7x – 12x2 + 6xy – 10xy + 2y2 + 5y2
= – 5x2 – 4xy + 7y2
(iii) P – Q + R
= (– 12x2 – 10xy + 5y2) – (7x2 + 6xy + 2y2) + (5x2 + 2xy + 4y2)
= – 12x2 – 10xy + 5y2 – 7x2 – 6xy – 2y2 + 5x2 + 2xy + 4y2
= – 12x2 – 7x2 + 5x2 – 10xy – 6xy + 2xy + 5y2 – 2y2 + 4y2
= – 14x2 – 14xy + 7y2
(iv) P + Q + R
= (– 12x2 – 10xy + 5y2) + (7x2 + 6xy + 2y2) + (5x2 + 2xy + 4y2)
= – 12x2 + 7x2 + 5x2 − 10xy + 6xy + 2xy + 5y2 + 2y2 + 4y2
= 0 − 2xy + 11y2
= − 2xy + 11y2
Question -5.
If x = a2 – bc, y = b2 – ca and z = c2 – ab ; find the value of :
(i) ax + by + cz
(ii) ay – bx + cz
Answer-5
(i) ax +by + cz
= a (a2 − bc) + b (b2 − ca) + c (c2 − ab)
= a3− abc + b3 − abc + c3 − abc
= a3 + b3 + c3 − 3abc
(ii) ay – bx + cz
= a (b2 − ca) − b (a2 − bc) + c (c2 − ab)
= ab2 − ca2 − a2b + b2c + c3 − abc
Question -6.
Multiply and then evaluate :
(i) (4x + y) and (x – 2y); when x = 2 and y = 1.
(ii) (x2 – y) and (xy – y2); when x = 1 and y = 2.
(iii) (x – 2y + z) and (x – 3z); when x = -2, y = -1 and z = 1.
Answer-6
(i) (4x + y) × (x − 2y)
= 4x (x − 2y) + y (x − 2y)
= 4x2 − 8xy + xy − 2y2
= 4x2 − 7xy − 2y2
Verification:
When x = 2, y = 1
L.H.S. = (4x + y) (x − 2y)
= (4 × 2 + 1) (2 − 2 × 1)
= (8 + 1) (2 − 2)
= 9 × 0
= 0
R.H.S. = 4x2 − 7xy − 2y2
= 4 (2)2 − 7 × 2 × 1 − 2 (1)2
= 4 × 4 − 14 − 2
= 16 − 16
= 0
∴ L.H.S. = R.H.S.
(ii) (x2 − y) × (xy − y2)
= x2 (xy − y2) − y (xy − y2)
= x3y − x2y2 − xy2 + y3
Verification:
When x = 1, y = 2
∴ L.H.S. = (x2 − y) (xy − y2)
= [(1)2 − 2] [1 × 2 − (2)2]
= (1 − 2) (2 − 4)
= − 1 × − 2
= 2
R.H.S. = x3y − x2y2 − xy2 + y3
= (1)3 × 2 − (1)2 (2)2 − 1(2)2 + (2)3
= 1 × 2 − 1 × 4 − 1 × 4 + 8
= 2 − 4 − 4 + 8
= 10 − 8
= 2
∴ L.H.S. = R.H.S.
(iii) (x − 2y + z) × (x − 3z)
= x (x − 3z) − 2y (x − 3z) + z (x − 3z)
= x2 − 2zx − 2xy + 6yz − 3z2
Verification:
When x = − 2, y = − 1, z = 1
L.H.S. = (x − 2y + z) × (x − 3z)
= [− 2 − 2 × (− 1) × 1] × [− 2 − 3 × 1]
= (− 2 + 2 + 1) × (− 2 − 3)
= 1 × (− 5)
= − 5
R.H.S. = x2 − 2zx − 2xy + 6yz − 3z2
= (− 2)2 − 2 (1) (− 2) − 2 (− 2) (− 1) + 6 (− 1) (1) − 3(1)2
= 4 + 4 − 4 − 6 − 3
= 8 − 13
= − 5
∴ L.H.S. = R.H.S.
Question -7. Substitution ICSE Class-6th Concise
Simplify :
(i) 5 (x + 3y) – 2 (3x – 4y)
(ii) 3x – 8 (5x – 10)
(iii) 6 {3x – 8 (5x – 10)}
(iv) 3x – 6 {3x – 8 (5x – 10)}
(v) 2 (3x2 – 4x – 8) – (3 – 5x – 2x2)
(vi) ![]()
(vii) ![]()
Answer-7
(i) 5 (x + 3y) – 2 (3x – 4y)
= 5x + 15y – 6x + 8y
= 5x – 6x + 15y + 8y
= – x + 23y
(ii) 3x – 8 (5x – 10)
= 3x – 40x + 80
= – 37x + 80
(iii) 6 {3x – 8 (5x – 10)}
= 6 {3x – 40x + 80}
= 18x – 240x + 480
= – 222x + 480
(iv) 3x – 6 {3x – 8 (5x – 10)}
= 3x – 6 {3x – 40x + 80}
= 3x – 18x + 240x – 480
= 243x – 18x – 480
= 225x – 480
(v) 2 (3x2 – 4x – 8) – (3 – 5x – 2x2)
= (6x2 – 8x – 16) – (3 – 5x – 2x2)
= 6x2 – 8x – 16 – 3 + 5x + 2x2
= 6x2 + 2x2 – 8x + 5x – 16 – 3
= 8x2 – 3x – 19
(vi)
![]()
= 8x − (3x − 2x + 3)
= 8x − 3x + 2x − 3
= 10x − 3x − 3
= 7x − 3
(vii)
![]()
= 12x2 − (7x − 3x2 − 15)
= 12x2 − 7x + 3x2 + 15
= 12x2 + 3x2 − 7x + 15
= 15x2 − 7x + 15
Question- 8.
If x = -3, find the value of : 2x3 + 8x2 – 15.
Answer-8
∴ 2x3 + 8x2 – 15
putting x = -3
= 2 (– 3)3 + 8 (– 3)2 – 15
= 2 (– 27) + 8 (9) – 15
= – 54 + 72 – 15
= – 54 – 15 + 72
= – 69 + 72
= 3
End of Substitution ICSE Class-6th Concise Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -6
Thanks