Surface Area Volume Capacity ICSE Class-8th Concise Selina Mathematics Solutions Chapter-21 . We provide step by step Solutions of Exercise / lesson-21 Surface Area Volume and Capacity (Cuboid, Cube and Cylinder ) for ICSE Class-8 Concise Selina Mathematics.
Our Solutions contain all type Questions with Exe-21 A, Exe-21 B Exe-21 C, Exe-21 D and Exe-21 E to develop skill and confidence . Visit official Website CISCE for detail information about ICSE Board Class-8 Mathematics.
Surface Area Volume Capacity ICSE Class-8th Concise Selina Mathematics Solutions Chapter-21 (Cuboid, Cube and Cylinder )
–: Select Topics :–
Exercise – 21 A Surface Area Volume Capacity ICSE Class-8th Concise Mathematics Selina Solutions (Cuboid, Cube and Cylinder )
Question 1.
Find the volume and the total surface area of a cuboid, whose :
(i) length = 15 cm, breadth = 10 cm and height = 8 cm.
(ii) l = 3.5 m, b = 2.6 m and h = 90 cm,
Answer
(i) Length =15 cm, Breadth = 10 cm, Height = 8 cm.
Volume of a cuboid = Length x Breadth x Height = 15 x 10 x 8 =1200 cm3.
Total surface area of a cuboid 2 (l x b + b x h + h x l) = 2 (15 x 10 + 10 x 8 + 8 x 15) = 2(150 + 80 +120) = 2 x 350 = 700 cm2
(ii) Length = 3.5 m Breadth = 2.6 m, Height = 90 cm = 90/100 m = 0.9 m.
Volume of a cuboid = l x b x h = 3.5 x 2.6 x 0.9 = 8.19 m3
Total surface area of a cuboid = 2(l x b + b x h + h x l)
= 2 (3.5 x 2.6 + 2.6 x 0.9 + 0.9 x 3.5) = 2 (910 + 2.34 + 3.15) = 2(14.59)= 29.18 m2
Question 2.
(i) The volume of a cuboid is 3456 cm3. If its length = 24 cm and breadth = 18 cm ; find its height.
(ii) The volume of a cuboid is 7.68 m3. If its length = 3.2 m and height = 1.0 m; find its breadth.
(iii) The breadth and height of a rectangular solid are 1.20 m and 80 cm respectively. If the volume of the cuboid is 1.92 m3; find its length.
Answer
 <
<

Question 3.
The length, breadth and height of a cuboid are in the ratio 5 : 3 : 2. If its volume is 240 cm3; find its dimensions. (Dimensions means : its length, breadth and height). Also find the total surface area of the cuboid.
Answer
Length of the given cuboid = 5x
Breadth of the given cuboid = 3x
Height of the given cuboid = 2x
Volume of the given cuboid = Length x Breadth x Height
= 5x x 3x x 2x = 30x3
But we are given volume = 240 cm3
30x3 = 240 cm3
⇒ x3 = 240/30
⇒ x3 = 8
⇒ x = 813
⇒ x = (2×2×2)13
⇒ x = 2 cm
Length of the given cube = 5x = 5 x 2 = 10 cm
Breadth of the given cube = 3x = 3 x 2 = 6 cm
Height of the given cube = 2x = 2 x 2 = 4cm
Total surface area of the given cuboid = 2(l x b + b x h + h x l)
= 2(10 x 6 + 6 x 4 + 4 x 10) = 2(60 + 24 + 40) = 2 x 124
= 248 cm2
The length, breadth and height of a cuboid are in the ratio 6 : 5 : 3. If its total surface area is 504 cm2; find its dimensions. Also, find the volume of the cuboid.
Answer
Length of the cuboid = 6x
Breadth of the cuboid = 5x
Height of the cuboid = 3x
Total surface area of the given cuboid = 2 (I x b + b x h + h x l)
= 2(6x x 5x + 5x x 3x + 3x x 6x) = 2(30×2 + 15×2 + 18×2)
= 2 x 63×2 = 126x2
But we are given total surface area of the given cuboid = 504 cm2
126x2 = 504 cm2
=> x2 = 504/126
=> x2 = 4
=> x = √4
=> x = 2 cm.
Length of the cuboid = 6x = 6 x 2 = 12 cm
Breadth of the cuboid = 5x = 5 x 2 = 10cm
Height of the cuboid = 3x = 3 x 2 = 6 cm
Volume of the cuboid = l x b x h = 12 x 10 x 6 = 720 cm3
Find the volume and total surface area of a cube whose each edge is :
(i) 8 cm
(ii) 2 m 40 cm.
Answer
(i) Edge of the given cube = 8 cm
Volume of the given cube = (Edge)3 = (8)3 = 8 x 8 x 8
= 512 cm3
Total surface area of a cube = 6(Edge)2 = 6 x (8)2
= 384 cm2
(ii) Edge of the given cube = 2 m 40 cm
= 2.40 m
Volume of a cube = (Edge)3
Volume of the given cube = (2.40)3 = 2.40 x 2.40 x 2.40
= 13.824 m2
Total surface area of the given cube = 6 x 2.4 x 2.4 = 34.56 m2
Question 6.
Find the length of each edge of a cube, if its volume is :
(i) 216 cm3
(ii) 1.728 m3
Answer
(i)

= Edge = 6 cm.
(ii)

= Edge = 1.2 m
Question 7.
The total surface area of a cube is 216 cm2. Find its volume.
Answer
6(Edge)2 = Total surface area of a cube
6(Edge)2 = 216 cm2
=> (Edge)2 = 216/6
=> (Edge)2 = √36
=> Edge = 36
=> Edge = 6 cm
Volume of the given cube = (Edge)3 = (6)3
= 6 x 6 x 6
= 216 cm3
Question 8.
A solid cuboid of metal has dimensions 24 cm, 18 cm and 4 cm. Find its volume.
Answer
Length of the cuboid = 24 cm
Breadth of the cuboid = 18 cm
Height of the cuboid = 4 cm
Volume of the cuboid = l x b x h = 24 x 18 x 4
= 1728 cm3
Question 9.
A wall 9 m long, 6 m high and 20 cm thick, is to be constructed using bricks of dimensions 30 cm, 15 cm and 10 cm. How many bricks will be required.
Answer
Length of the wall = 9 m = 9 x 100 cm = 900 cm
Height of the wall = 6 m = 6 x 100 cm = 600 cm
Breadth of the wall = 20 cm
Volume of the wall = 900 x 600 x 20 cm3 = 10800000 cm3
Volume of one Brick = 30 x 15 x 10 cm3 = 4500 cm3
Number of bricks required to construct the wall = Volume of wall/Volume of one brick
= 10800000/4500
= 2400
Question 10.
A solid cube of edge 14 cm is melted down and recanted into smaller and equal cubes each of edge 2 cm; find the number of smaller cubes obtained.
Answer
Edge of the big solid cube = 14 cm
Volume of the big solid cube = 14 x 14 x 14 cm3 = 2744 cm3
Edge of the small cube = 2 cm
Volume of one small cube = 2 x 2 x 2 cm3 = 8 cm3
Number of smaller cubes obtained = Volume of big cube/Volume of one small cube
= 2744/8
=343
Question 11.
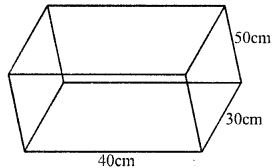
A closed box is cuboid in shape with length = 40 cm, breadth = 30 cm and height = 50 cm. It is made of thin metal sheet. Find the cost of metal sheet required to make 20 such boxes, if 1 m2 of metal sheet costs Rs. 45.
Answer
Length of closed box (l) = 40 cm
Breadth (b) = 30 cm
and height (h) = 50 cm
Total surface area = 2 (lb + bh + hl)
= 2 (40 x 30 + 30 x 50 + 50 x 40) cm2
= 2 (1200 + 1500 + 2000) cm2
= 2 x 4700 = 9400 cm2
Surface area of sheet used for 20 such boxes = 9400 x 20 = 188000 cm2
Cost of 1 m2 sheet = Rs. 45
Total cost = (18000×45)/(100×100×100)
= Rs.846
Question 12.
Four cubes, each of edge 9 cm, are joined as shown below :

Write the dimensions of the resulting cuboid obtained. Also, find the total surface area and the volume of the resulting cuboid.
Answer
Edge of each cube = 9 cm
(i) Length of the cuboid fonned by 4 cubes (l) = 9 x 4 = 36 cm
Breadth (b) = 9 cm and height (h) = 9 cm
(ii) Total surface area of the cuboid = 2(lb + bh + hl)
= 2 (36 x 9 + 9 x 9 + 9 x 36) cm2
= 2 (324 + 81 + 324) cm2
= 2 x 729 cm2
= 1458 cm2
(iii) Volume = l x b x h = 36 x 9 x 9 cm2 = 2916 cm3
Surface Area Volume Capacity Exe-21 B ICSE Class-8th Concise Mathematics Selina Solutions (Cuboid, Cube and Cylinder )
Question 1.
How many persons can be accommodated in a big-hall of dimensions 40 m, 25 m and 15 m ; assuming that each person requires 5 m3 of air?
Answer

Length of the hall = 40 m
breadth = 25 m
Height = 15 m
Volume of the hall = L×B×H
= 40×25×15
= 15000 m3
The volume of the air required for each person = 5m3

= 15000m3/5m3
= 3000
Question 2.
The dimension of a class-room are; length = 15 m, breadth = 12 m and height = 7.5 m. Find, how many children can be accommodated in this class-room ; assuming 3.6 m3 of air is needed for each child.
Answer
Length of the room = 15 m
Breadth of the room = 12 m
Height of the room = 7.5 m
Volume of the room = L x B x H = 15 x 12 x 7.5 m3 = 1350 m3
Volume of air required for each child = 3.6 m3
No. of children who can be accommodated in the classroom.
= 1350m3/3.6m3
= 375
Question 3.
The length, breadth and height of a room are 6 m, 5.4 m and 4 m respectively. Find the area of :
(i) its four-walls
(ii) its roof.
Answer
Length of the room = 6 m
The breadth of the room = 5.4 m
Height of the room = 4 m
(i) Area of four walls = 2(L+B) x H
= 2(6 + 5.4) x 4 = 2 x 11.4 x 4 = 91.2 m2
(ii) Area of the roof = L x B = 6 x 5.4 = 32.4 m2
Question 4.
A room 5 m long, 4.5 m wide and 3.6 m high has one door 1.5 m by 2.4 m and two windows, each 1 m by 0.75 m. Find :
(i) the area of its walls, excluding door and windows ;
(ii) the cost of distempering its walls at the rate of Rs.4.50 per m2.
(iii) the cost of painting its roof at the rate of Rs.9 per m2.
Answer
Length of the room = 5 m
The breadth of the room = 4.5 m
Height of the room = 3.6 m
Area of the roof = L×B
= 5×4.5m2
= 22.5 m2
Area of four walls = 2[L + B] × H
= 2[5 + 4.5] × 3.6
= 2(9.5) × 3.6
= 19 × 3.6
= 68.4 m2
Area of one door = 1.5×2.4m2
= 3.60 m2
= 3.6 m2
Area of one window = 1×0.75m2
= 0.75 m2
Area of 2 window = 0.75×2m2
= 1.5 m2
(i) Area of four walls excluding door and windows = 68.4 – (3.6 + 1.5)
= 68.4 – 5.1
= 63.3 m2
(ii) Cost of distempering four walls @ Rs. 4.50 per m2
= 63.3 × 4.50
= Rs. 284.85
(iii) Cost of painting the roof @ Rs.9 per m2
= 22.5 × 9
= Rs. 202.50
Question 5.
The dining-hall of a hotel is 75 m long ; 60 m broad and 16 m high. It has five – doors 4 m by 3 m each and four windows 3 m by 1.6 m each. Find the cost of :
(i) papering its walls at the rate of Rs.12 per m2;
(ii) carpeting its floor at the rate of Rs.25 per m2.
Answer
Length of the dining hall of a hotel = 75 m
The breadth of the dining hall of a hotel = 60 m
Height of the dining hall of a hotel = 16 m
(i) Area of four walls of the dining hall = 2[L+B) x H = 2(75 + 60) x 16
= 2(135)×16
= 270×16
= 4320 m2
Area of one door = 4×3 m2
= 12 m2
Area of 5 doors = 12×5=60 m2
Area of one window = 3×1.6=4.8m2
Area of 4 window = 4.8×4=19.2m2
Area of the walls to be papered
= 4320 – (60 + 19.2)
= 4320 – 79.2
= 4240.8 m2
Cost of papering the walls @ Rs.12 per m2
= 4240.8×12
= Rs. 50889.60
(ii) Area of floor = L × B
= 75×60
= 4500 m2
Cost of carpeting the floor @ Rs. 25 per m2
= 4500 × 25
= Rs. 112500
Question 6.
Find the volume of wood required to make a closed box of external dimensions 80 cm, 75 cm and 60 cm, the thickness of walls of the box being 2 cm throughout.
Answer
External length of the closed box = 80 cm
External Breadth of the closed box = 75 cm
External Height of the closed box = 60 cm
External volume of the closed box = 80 x 75 x 60 = 360000 cm3
Internal length of the closed box = 80 – 4 = 76 cm
Internal Breadth of the closed box = 75 – 4 = 71 cm
Internal Height of the closed box = 60 – 4=56 cm
Internal volume of the closed box = 76 x 71 x 56 cm = 302176 cm3
Volume of wood required to make the closed box = 360000 – 302176 = 57824 cm3
Question 7.
A closed box measures 66 cm, 36 cm and 21 cm from outside. If its walls are made of metal-sheet, 0.5 cm thick ; find :
(i) the capacity of the box ;
(ii) volume of metal-sheet and
(iii) weight of the box, if 1 cm3 of metal weights 3.6 gm.
Answer
External length of the closed box = 66cm.
External breadth of the closed box = 36 cm
External height of the closed box =21 cm
External volume of the closed box= 66 x 36 x 21 = 49896 cm3
Internal length of the box =(66 – 2 x 0.5) = 66 – 1 = 65 cm
Internal breadth of the box =(36 – 2 x 0.5) = 36 – 1 = 35 cm
Internal height of the box = (21 – 2 x 0.5) = 21 – 1 = 20 cm
Internal Volume of the box = 65 x 35 x 20 = 45500 cm3
(i) Capacity of the box = 45500 cm3
(ii) Volume of metal sheet of the box = External volume – Internal volume
= 49896 – 45500 = 4396 cm3
(iii) 1 cm3 of metal weigh 3.6 grams.
Weight of the box = 4396 x 3.6 gm = 15825.6 gm
Question 8.
The internal length, breadth and height of a closed box are 1 m, 80 cm and 25 cm. respectively. If its sides are made of 2.5 cm thick wood ; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
Answer
Internal length of the closed box = 1m
= 100 cm
breadth = 80 cm
height = 25 cm
volume = 100×80×25
= 200000 cm3
External length of the box = (100+2×2.5)
= 100 + 5 = 105 cm
External breadth = (80+2×2.5)
= 80 + 5 = 85 cm
External height = (25+2×2.5)
= (25 + 5) = 30 cm
External volume = 105×85×30 cm3
= 267750 cm3
(i) The capacity of the box = 100×80×25 cm3
= 200000 cm3
= (200000)/100×100×100 m3
= 0.2 m3
(ii) The volume of wood used to make the box
= External volume – Internal volume
= 267750 – 200000
= 67750 cm3
= (67750)/100×100×100m3
= 0.06775 m3
Question 9.
Find the area of metal-sheet required to make an open tank of length = 10 m, breadth = 7.5 m and depth = 3.8 m.
Answer
Length of the tank = 10 m
Breadth of the tank = 7.5 m
Depth of the tank = 3.8 m
Area of four walls = 2[L+B] x H = 2(10 + 7.5) x 3.8
= 2 x 17.5 x 3.8 = 35 x 3.8 = 133 m2
Area of the floor = L x B = 10 x 7.5 = 75 m
Area of metal sheet required to make the tank =Area of four walls + Area of floor = 133 m2 + 75 m2 = 208 m2
Question 10.
A tank 30 m long, 24 m wide and 4.5 m deep is to be made. It is open from the top. Find the cost of iron-sheet required, at the rate of ₹ 65 per m2, to make the tank.
Answer:
Length of the tank = 30 m
Width of the tank = 24 m
Depth of the tank = 4.5 m
Area of four walls of the tank = 2[L+B] x H = 2(30 + 24) x 4.5 = 2 x 54 x 4.5 m2 = 486 m2
Area of the floor of the tank = L x B = 30 x 24 = 720 m2
Area of Iron sheet required to make the tank = Area of four walls + Area of floor = 486 + 720 = 1206 m2
Cost of iron sheet required @ ₹ 65 per m2 = 1206 x 65 = ₹ 78390
Selina Solutions of Concise Maths Surface Area Volume Capacity for ICSE Class-8th Exercise – 21 C (Cuboid, Cube and Cylinder )
Question 1.
The edges of three solid cubes are 6 cm, 8 cm and 10 cm. These cubes are melted and recast into a single cube. Find the edge of the resulting cube.
Answer
Edge of first solid cube = 6 cm
Volume = (6)3
= 216 cm3
Edge of second cube = 8 cm
Volume = (8)3
= 512 cm3
Edge of third cube = 10 cm
Volume = (10)3 = 1000 cm3
Sum of volumes of three cubes = 216 + 512 + 1000
= 1728 cm3
Let a be the edge of so formed cube volume = a3
a3 = 1728 = (12)3
a = 12 cm
Question 2.
Three solid cubes of edges 6 cm, 10 cm and x cm are melted to form a single cube of edge 12 cm, find the value of x.
Answer
Edge of first cube = 6 cm
Volume = (6)3 = 216 cm3
Edge of second cube = 10 cm
Volume = (10)3 = 1000 cm3
Edge of third cube = x
Volume =x3
Edge of resulting cube = 12 cm
Volume = (12)3
= 1728 cm3
216 + 1000 + x3
= 1728
x3 = 1728 – 216 – 1000 = 512
= (8)3
x = 8
Edge of third cube = 8 cm
Question 3.
The length of the diagonals of a cube is 8√3 cm.
Find its:
(i) edge
(ii) total surface area
(iii) Volume
Answer
(i) Length of diagonal of a cube = 8√3 cm
Length of edge = 8√3/√3 = 8 cm
(ii) Total surface area = 6a2 = 6 x 82 = 6 x 64 cm2 = 384 cm2
(iii) Volume = a3 = (8)3= 512 cm3
Question 4.
A cube of edge 6 cm and a cuboid with dimensions 4 cm x x cm x 15 cm are equal in volume. Find:
(i) the value of x.
(ii) total surface area of the cuboid.
(iii) total surface area of the cube.
(iv) which of these two has greater surface and by how much?
Answer
Edge of a cube = 6 cm
Volume = a3 = (6)3 = 216 cm3
Dimensions of a cuboid = 4 cm x x cm x 15 cm
Volume = 60x cm3
The volume of both is equal
(i) ∴ 60x=216
x = 216/60 = 36/10
∴ x = 3.6 cm
(ii) Total surface area of cuboid
= 2[lb + bh + hl]
= 2[4×3.6+3.6×15+15×4] cm2
= 2[14.4 + 54.0 + 60] cm2
= 128.4×2=256.8 cm2
(iii) Total surface area of cube
= 6a²=6(6)²=6×36=216 cm2
(iv) Difference of surface areas = 256.8 – 216
= 40.8 cm2
∴ Surface area of cuboid is greater
Question 5.
The capacity of a rectangular tank is 5.2 m3 and the area of its base is 2.6 x 104 cm2; find its height (depth).
Answer
Capacity of a tank = 5.2 m3
and area of its base = 2.6 x 104 cm2
= (2.6×10000)/(100×100) =2.6m2
⇒ lb = 2.6 m2
and l bh = 5.2 m3
∴ Height (h) = 5.2/2.6 = 2m
Question 6.
The height of a rectangular solid is 5 times its width and its length is 8 times its height. If the volume of the wall is 102.4 cm3, find its length.
Answer
Height of rectangular solid = 5 x width
and length = 8 x height = 8 x 5 x width = 40 x width
Volume = 102.4 cm3
Let width = w
Then height = 40w
and height = 5w
∴ w × 40w × 5w = 102.4
w³= (102.4)/40×5= 0.512
= (0.8)3
∴ w = 0.8
∴ Length = 40w = 40×0.8 = 32 cm
Question 7.
The ratio between the lengths of the edges of two cubes are in the ratio 3 : 2. Find the ratio between their:
(i) total surface area
(ii) volume.
Answer
Ratio in edges of two cubes = 3:2
Let edge of first cube = 3x
Then edge of second cube = 2x
(i) Now total surface area of first cube = 6 x (3x)2
= 6 x 9x2 = 54x2
and of surface area of second cube = 6 x (2x)2
= 6 x 4x2 = 24x2
Ratio = 54x2: 24x2 = 9:4
(ii) Volume of first cube = (3x)3
= 27x3
and second cube = (2x)3 = 8x3
Ratio = 27x3: 8x3
= 27 :8
Question 8.
The length, breadth and height of a cuboid (rectangular solid) are 4 : 3 : 2.
(i) If its surface are is 2548 cm2, find its volume.
(ii) If its volume is 3000 m3, find its surface area.
Answer
Surface area of cuboid = 2548 cm2
Ratio in length, breadth and height of a cuboid = 4 : 3 : 2
Let length = 4x, Breadth = 3x and height = 2x
∴Surface area=2(4x×3x+3x×2x+2x×4x)
= 2(12x²+6x²+8x²)
= 2×26x²=52×2
∴ 52x²=2548
x²= 2548/52 =49=(7)²
∴x=7
∴Length=4x=4×7=28 cm
∴Breadth=3x=3×7=21 cm
and height=2x=2×7=14cm
∴Volume=lbh
=28×21×14 cm3 = 8232 cm2
(ii) If volume = 3000 m3
⇒ 4x×3x×2x=3000
⇒ 24x³=3000
⇒ x³ = 3000/24 = 125 = (5)³
∴x=5m
Length=5×4=20,breadth=5×3=15m
and height = 5×2=10m
∴Surface area=2 [ lb + bh + hl ]
= 2[20×15+15×10+10×20]m2
= 2[300+150+200]m2
= 2×650=1300m2
Exercise – 21 D Surface Area Volume Capacity ICSE Class-8th Mathematics Selina Solutions (Cuboid, Cube and Cylinder )
Question 1.
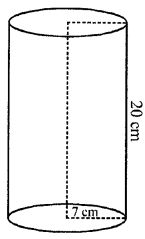
The height of a circular cylinder is 20 cm and the diameter of its base is 14 cm. Find:
(i) the volume
(ii) the total surface area.
Answer
Height of cylinder (h) = 20 cm
and diameter of its base (d)= 14 cm
and radius of its base (r)= 14/2 = 7 cm
(i) Volume = πr2h
= (22/7)×7×7×20 cm3 = 3080 cm3
(ii) Total surface area = 2πr(h + r)
= 2×(22/7)×7(20+7) cm2 = 44 x 27 = 1188 cm2
Question 2.
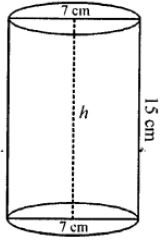
Find the curved surface area and the total surface area of a right circular cylinder whose height is 15 cm and the diameter of the cross-section is 14 cm.
Answer
Diameter of the base of cylinder = 14 cm
Radius (r) = 14/2 cm = 7 cm
Height (h) = 15 cm
Curved surface area = 2πrh
= 2×(22/7)×7×15
= 660 cm2
Total surface area
= 2πr (h + r)
= 2×(22/7)×7(15+7)
= 2×(22/7)×7×22
= 968 cm2
Question 3.
Find the height of the cylinder whose radius is 7 cm and the total surface area is 1100 cm2.
Answer
Total surface area =1100 cm2
Radius = 7 cm
Let height of the cylinder = h
Then, total surface area = 2πr(h + r)
⇒ 2×(22/7)×7(h+7)=1100
⇒ 44(h+7)=1100
⇒ 44h+308=1100
⇒ 44h=1100-308
h = 792/44=18 cm
Question 4.
The curved surface area of a cylinder of height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
Answer
Height (h) = 14 cm
Curved surface area (2πrh) = 88 cm2
Then, 2πrh = 88 cm2
⇒ 2×(22/7)×r×14=88cm2
⇒ 88r = 88
⇒ r = 88/88=1 cm
Then diameter = 1×2=2 cm
Question 5.
The ratio between the curved surface area and the total surface area of a cylinder is 1 : 2. Find the ratio between the height and the radius of the cylinder.
Answer
r be the radius and h be the height of a right circular cylinder, then Curved surface area = 2πrh
and total surface area = 2πrh x 2πr2 = 2πr(h + r)
But their ratio is 1: 2
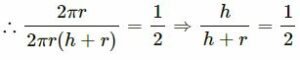
2h = h + r ⇒ 2h – h = r
h = r = 1 : 1
Hence their radius and height are equal
Question 6.
Find the capacity of a cylindrical container with internal diameter 28 cm and height 20 cm.
Answer
Diameter = 28 cm
Radius = 28/2 cm = 14 cm
Height = 20 cm
Volume = πr2h = (22/7) x 14 x 14 x 20
Volume = 12320 cm3
Question 7.
The total surface area of a cylinder is 6512 cm2 and the circumference of its bases is 88 cm. Find:
(i) its radius
(ii) its volume
Answer
Let r be the radius and h be the height of the given cylinder.
Circumference = 2πr = 88 cm (Given)
⇒ 2×(22/7)×r=88cm
⇒ r=88×(7/22)×(1/2)
⇒ r = 14 cm
Total surface area = 2πr(h+r)
=6512 cm2 (Given)
⇒ 88(h+14)=6512
(∵ 2πr=88 cm and r = 14 cm)
⇒ h+14=6512/88
⇒ h + 14 = 74 ⇒ h = 60 cm
∴ Volume of the cylinder = πr²h
= (22/7)×(14)²×60 cm3 = 36960 cm3
Question 8.
The sum of the radius and the height of a cylinder is 37 cm and the total surface area of the cylinder is 1628 cm2. Find the height and the volume of the cylinder.
Answer
Let r and h be the radius and height of the solid cylinder respectively.
Given, r + h = 37 cm
The total surface area of the cylinder = 1628 cm2 (Given)
∴ 2πr(r+h)=1628cm2
⇒ 2πr×37=1628 cm2
⇒ 2×(22/7)×r×37=1628cm2
⇒ r=(1628×7)/(2×22×37)=7 cm
rth = 37 cm ⇒ 7 + h = 37 cm ⇒ h = 30 cm
The volume of the cylinder = πr²h
= (22/7)×7×7×30=4620 cm3
Question 9.
A cylindrical pillar has radius 21 cm and height 4 m. Find :
(i) the curved surface area of the pillar
(ii) cost of polishing 36 such cylindrical pillars at the rate of ₹ 12 per m2.
Answer
Radius of the cylinder = 21 cm
= 21/100=2.1m
Height of the cylinder = 4 m
(i) Curved surface area of the cylinder = 2πrh
= 2×(22/7)×2.1×4=52.8 m2
(ii) Cost of polishing 1 m2 = ₹ 12
Cost of polishing (36×52.8m²)
= ₹ 12×1900.80
= ₹ 22,809.60
Question 10.
If radii of two cylinders are in the ratio 4 : 3 and their heights are in the ratio 5 : 6, find the ratio of their curved surfaces.
Answer
The ratio in radii of two cylinders = 4 : 3
and ratio in their heights = 5: 6
Let r1 and r2 be the radii and h1,h2 be their heights respectively.
∴ r1 : r2 = 4:3 and h1 : h2 = 5:6

∴ Ratio in their surface areas = 10 : 9
Concise Mathematics Exercise – 21 E Surface Area Volume and Capacity (Cuboid, Cube and Cylinder ) for ICSE Class-8th
Question 1.
A cuboid is 8 m long, 12 m broad and 3.5 high, Find its
(i) total surface area
(ii) lateral surface area
Answer
Length of a cuboid = 8 m
The breadth of a cuboid = 12 m
Height of a cuboid = 3.5 m
(i) Total surface area = 2(lb + bh + hl)
= 2(8 x 12 + 12 x 3.5 + 3.5 x 8)
= 2(96 + 42 + 28)
= 2 x 166 = 332 m2
(ii) Lateral surface area = 2h(l + b)
= 2 x 3.5(8 + 12) = 7 x 20= 140 m2
Question 2.
How many bricks will be required for constructing a wall which is 16 m long, 3 m high and 22.5 cm thick, if each brick measures 25 cm x 11.25 cm x 6 cm?
Answer
Length of the wall = 16 m = 16 x 100 cm = 1600 cm
Height of the wall = 3 m = 3 x 100 cm = 300 cm
Breadth of the wall = 22.5 cm
Volume of the wall = 1600 x 300 x 22.5 cm3 = 1,08,00,000 cm3
Volume of one brick = 25 x 11.25 x 6 cm3 = 1687.5 cm3
Number of bricks required to construct the wall = (Volume of wall/Volume of one brick)
= (1,08,00,000/1687.5)=6400
Question 3
The length, breadth and height of cuboid are in the ratio 6 : 5 : 3. If its total surface area is 504 cm2, find its volume.
Answer
Let the length of the given cuboid = 6x
The breadth of the given cuboid = 5x
Height of the given cuboid = 3x
The total surface area of the given cuboid
= 2(lb + bh + hl)
= 2(6x×5x+5x×3x+3x×6x)
= (30x²+15x²+18x²)
= 2×63x²=126x²
But, we are given total surface area
= 504 cm2
∴ 126x2 = 504
⇒ x²=504126
⇒ x²=4
⇒ x²=(2)²
⇒ x = 2 cm
∴ Length of the given cuboid = 6x
= 6×2cm
=12 cm
Breadth of the given cuboid = 5x
= 5×2 cm = 10 cm
Height of the given cuboid = 3x
= 3×2 cm = 6 cm
Now, volume of the cuboid
= l×b×h
= 12×10×6
=720 cm3
Question 4.
The external dimensions of an open wooden box are 65 cm, 34 cm and 25 cm. If the box is made up of wood 2 cm thick, find the capacity of the box and the volume of wood used to make it.
Answer
External length of the open box = 65 cm
External breadth of the open box = 34 cm
External height of the open box = 25 cm
External volume of the open box = 65 x 34 x 25 cm3 = 55250 cm3
Internal length of open box = 65 – (2 x 2) cm = 61 cm
Internal breadth of a open box = 34 – (2 x 2) cm = 30 cm
Internal height of open box = 25 – 2 cm = 23 cm
Internal volume of open box or capacity of the box = 61 x 30 x 23 cm3 = 42090 cm3
Volume of wood required to make the closed box = 55250 – 42090 cm3 = 13160 cm3
Question 5.
The curved surface area and the volume of a toy, cylindrical in shape, are 132 cm2 and 462 cm3 respectively. Find, its diameter and its length.
Answer
et the radius of a toy = r and
height of the toy = h
The curved surface area of a toy = 132 cm2
=> 2πrh = 132 cm2
⇒ 2πrh = 132 cm2
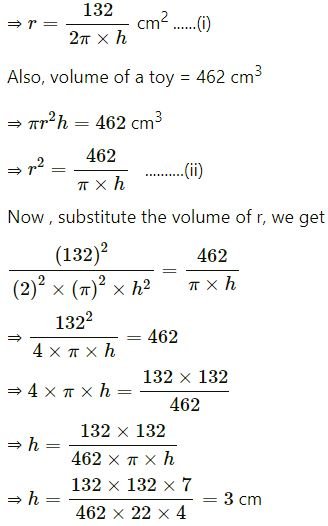
Now, put the value of h in eq. (i), we get
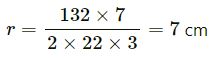
∴ Diameter of the toy = 2×r
= 2×7 cm = 14 cm
Question 6.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m2 is ₹ 15,000, find the height of the hall.
Answer
Let the length, breadth, and height of the rectangular hall be l m, b m, and h m respectively.
he perimeter of the floor of hall = 2(l + b)
250 m = 2(l + b)
(l + b) = 250/2=125 cm …(i)
Area of four walls = Area of cuboid – Area of floor – Area of top
= 2 (lb + bh + hl) – (l x b) – (l x b)
= 2(lb) + 2 (bh) + 2(hl) – 2lb = 2 lh + 2 bh
= 2h(l + b)
= 2h x 125 [From (i)]
= 250h m2
Area of four walls = 250h m2
Cost of painting 1 m2 area = ₹ 10
Cost of painting 250h m2 area = ₹ 10 x 250h = 2500h
15000 = 2500h
h = 15000/2500
The height of the hall is 6 m.
Question 7.
The length of a hall is double its breadth. Its height is 3 m. The area of its four walls (including doors and windows) is 108 m2, find its volume.
Answer
Let the breadth be x
and the length be 2x
Height = 3 m
Area of four walls = 108 m2
⇒ 2(l + b)h = 108
⇒ 2(2x + x)3 = 108
⇒ 6×3x=108
⇒ 3x = 108/6
⇒ x= 18/3 = 6m
∴ Breadth = x = 6 m
and length = 2x = 12 m
Hence, Volume = l×b×h
= 12×6×3
= 216 m3
Question 8.
A solid cube of side 12 cm is cut into 8 identical cubes. What will be the side of the new cube? Also, find the ratio between the surface area of the original cube and the total surface area of all the small cubes formed.
Answer
Here, the cube of side 12 cm is divided into 8 cubes of side 9 cm.

Given that,
Their volumes are equal.
The volume of big cube of 12 cm = Volume of 8 cubes of side a cm
(Side of the big cube)3 = 8 x (Side of the small cube)3
(12)3 = 8 x a3
⇒ a3=12×12×128
⇒ a3=63 cm3
⇒ a = 6 cm

So, the ratio is 1:2
Question 9.
The diameter of a garden roller is 1.4 m and it 2 m long. Find the maximum area covered by it 50 revolutions?
Answer
Diameter of the roller = 1.4 m
Radius (r) = 1.4/2
= 0.7 m
and length (h) = 2m
Curved surface area = 2πrh
= 2 x (22/7) x 0.7 x 2 cm2 = 8.8 m2
Area covered in 50 complete revolutions = 8.8 x 50 m2 = 440 m2
Area of the playground = 440 m2
Question 10.
In a building, there are 24 cylindrical pillars. For each pillar, radius is 28 m and height is 4 m. Find the total cost of painting the curved surface area of the pillars at the rate of ₹ 8 per m2.
Answer
— End of Surface Area Volume Capacity Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -8