The Circle ICSE Class-6th Concise Selina Mathematics Solutions Chapter-29. We provide step by step Solutions of Exercise / lesson-29 The Circle for ICSE Class-6 Concise Selina Mathematics.
Our Solutions contain all type Questions of Exe-29 A , Exe-29 B and Revision Exercise with Notes on “The Circle” to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6.
The Circle ICSE Class-6th Concise Selina Mathematics Solutions Chapter-29
–: Select Topics :–
Notes on The Circle
A circle is a simple closed curve and it is not a polygon. Below is the image of a circle.
Parts of a Circle
Centre: The center point of the entire circle. Point C is the centre of the circle.
Radius: The line segment that connects the centre of circle to any point on the circle. OC is the radius of the circle.
Diameter: The line segment that connects two points on the circle and passes through the centre of the circle. It is double the value of the radius. AB is the diameter of the circle.
Chord: The line segment that connects two points on the circle but do not pass through the centre of the circle. DE is the chord of the circle.
Circumference: It is the distance around the circle.
Arc: An arc is the part of circumference. DFE is the arc of the circle.
Sector: Sector is an interior region bounded by pair of radii and arc on one side. OBC is a sector of the circle where OB and OC are radius and BC is an arc.
Segment: Segment is an interior region bounded by a chord and an arc.
Also note that the Diameter is twice the Radius:
Diameter = 2 × Radius
And so this is also true:
Circumference = 2 × π × Radius
Area of Circle
The area of a circle is π times the radius squared, which is written:
A = π r2
Where
- A is the Area
- r is the radius
Exercise – 29 A The Circle ICSE Class-6th Concise Selina Mathematics Solutions
Question- 1.
Use the figure given below to fill in the blanks :
(i) R is the …… of the circle.
(ii) Diameter of a circle is …… .
(iii) Tangent to a circle is … .
(iv) EF is a …… of the circle.
(v) …… is a chord of the circle.
(vi) Diameter = 2 x …..
(vii) ……. is a radius of the circle.
(viii) If the length of RS is 5 cm, the length of PQ = ……
(ix) If PQ is 8 cm long, the length of RS =…..
(x) AB is a ….. of the circle

Answer-1
(i) center
(ii) PQ
(iii)AB
(iv) secant
(v) CD
(vi) radius
(vii) RS
(viii) 10 cm
(ix) 4 cm
(x) tangent.
Question -2.
Draw a circle of radius 4.2 cm. Mark its centre as O. Take a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Answer-2
(i) By measurement AB = 8.4 cm.
(ii) ∴ AB is the diameter of the circle.
Question-3
(i) 6 cm
(ii) 8.4 cm.
In each case, measure the length of the radius of the circle drawn.
Answer-3
(i) 6 cm
AB is the diameter of circle
i.e. AB = 6 cm
and OA is the radius of circle
=1⁄2 of diameter=6⁄2 =3 cm
i.e., OA = OB = 3 cm
(ii) 8.4 cm.
AB is the diameter of circle
i.e. AB = 8.4 cm
and OA is the radius of a circle
=1⁄2 of diameter=8.4⁄2 = 4.2 cm
i.e., OA = OB = 4.2 cm.
Question- 4.
Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the centre of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
Answer-4
(i)

(ii) Δ AOB is equilateral triangle.
(iii) By measurement ∠AOB = 60°
Question -5.
Draw a circle of radius 4.8 cm and mark its centre as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
Answer-5
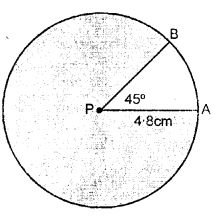
PA is the radius of circle. i.c., PA = 4.8 cm.
(i) ∠APB = 45° in which P is the centre of the circle and PA and PB are radii of circle.
(ii) Major sector of circle is shaded in the figure.
Question- 6.
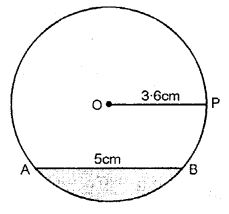
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
Answer-6
Shaded portion of circle is the minor segment of the circle.
Question- 7.
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Answer-7
In the figure, A is the centre of the circle and AB = 4 cm [radius of circle]

Question -8.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
Answer-8

By measurement ∠ACB =90
The Circle Exe-29 B ICSE Class-6th Concise Selina Mathematics
Question- 1.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
Answer-1
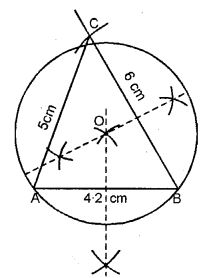
(i) Draw ∆ABC in which AB = 4.2 cm. BC = 6 cm. and AC = 5 cm.
(ii) Draw the perpendicular bisectors of any two sides of the triangle. Let these intersect at O.
(iii) Taking O as centre and OA or OB or OC as radius draw a circle.
This circle will pass through vertices A, B and C.
Question -2.
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°.
Construct the circumcircle of the triangle PQR.
Answer-2

(i) Draw a ∆PQR in which QR = 5.5 cm, ∠Q = 60° and ∠R = 45°.
(ii) Draw the arc bisector of PQ and PR which intersect at O.
(iii) Taking O as centre and radius OP or OQ or OR draw a circle.
This circle will pass through vertices P, Q and R.
Question -3.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm.
Draw the incircle of the triangle ABC.
Answer-3
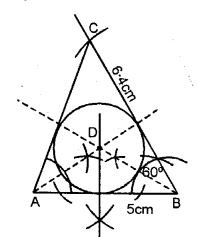
(i) Draw a line AB = 5 cm.
(ii)B as a centre draw an angle with the help of compass ∠B = 60°. Cut the line with an arc BC = 6 4 cm.
(iii) Join AC.
(iv) Now, from A and B cut the bisector of ∠A and ∠B, which intersect each other at point D.
(v) With D as a centre draw an incircle which touches all the three sides of AABC.
Question- 4.
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
Answer-4
(i) Draw a triangle XYZ in which XY = YZ = 4.5 cm and ZX = 5.4 cm.
(ii) Draw the bisectors of XZ and YZ which meet at O.
(iii) With O as centre and radius OX or OY or OZ draw a circle.
This circle will pass through X, Y and Z
Question -5.
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
Answer-5
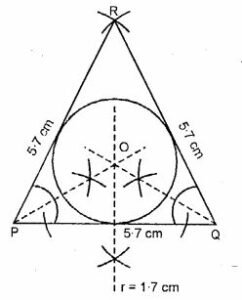
(i) Draw an equilateral ∆ RPQ in which PQ = QR = RP = 5.7 cm each.
(ii) From P and Q cut the bisector of ∠P and ∠Q, which intersect each other at point O.
(iii) With P as a centre draw an incircle which touches all the three sides of ∆RPQ.
Revision Exercise The Circle ICSE Class-6th Concise Mathematics Selina Solutions
Question- 1.
The centre of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when :
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
Answer-1
Draw circle each of radius 8 cm. With centre O
In figure
(a) draw OP = 10.6 cm
We see that point P lies outside the circle as OP > radius of the circle
(b) OP = 6.8 cm. We see that P lies inside the circle as OP < radius of the circle.
(c) OP = 8 cm. We see that P lies on the circle as OP = radius of the circle.
Question -2.
The diameter of a circle is 12.6 cm. State, the length of its radius.
Answer-2
Diameter of the circle = 12.6 cm
∴Radius = 1⁄2 diameter = 1⁄2 x 12.6 cm
= 6.3 cm
Question- 3.
Can the length of a chord of a circle be greater than its diameter ? Explain.
Answer-3
No, the length of chord cannot be greater than the diameter of the cirlce as the diameter of a circle is the greatest chord of that circle
Question- 4.
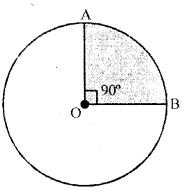
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
Answer-4
Draw a circle with diameter = 7 cm
OA and OB are the radii of the circle such that ∠AOB = 90°
Now shade the minor sector AOB This is the quadrant of the circle
Question -5.
State, which of following statements are true and which are false :
(i) If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
(ii) The longest chord of a circle is its diameter.
(iii) Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
(iv) The diameters of a circle always pass through the same point in the circle.
Answer-5
(i) False, as AB may be diameter or may not be, it can be chord.
(ii) True, diameter of a circle is the longest chord.
(iii) True.
(iv) True, all the diameter of a circle pass through the same point i.e., centre, of the circle.
–: End of Circle ICSE Class-6th Concise Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -6
Thanks


