ML Aggarwal Triangles Exe-10.1 Class 9 ICSE Maths APC Understanding Solutions. Solutions of Exercise-10.1. This post is the Solutions of ML Aggarwal Chapter 10- Triangles for ICSE Maths Class-9. APC Understanding ML Aggarwal Solutions (APC) Avichal Publication Solutions of Chapter-10 Triangles for ICSE Board Class-9. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Triangles Exe-10.1 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 9th |
| Chapter-10 | Triangles |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-10.1 Questions |
| Edition | 2021-2022 |
Exe-10.1 Solutions of ML Aggarwal for ICSE Class-9 Ch-10, Triangles
Note:- Before viewing Solutions of Chapter -10 Triangles Class-9 of ML Aggarwal Solutions . Read the Chapter Carefully. Then solve all example given in Exercise-10.1, Exercise-10.2, Exercise-10.3, Exercise-10.4, MCQs, Chapter Test.
Triangles Exe-10.1
ML Aggarwal Class 9 ICSE Maths Solutions
Page 190
Question 1. It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR ? Why?
Solution:
Given ∆ABC ≅ ∆RPQ
Therefore, their corresponding sides and angles are equal.
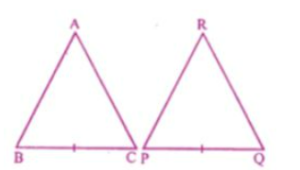
Therefore BC = PQ
Hence it is not true to say that BC = QR
Triangles Exe-10.1
ML Aggarwal Class 9 ICSE Maths Solutions
Page 191
Question 2. “If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Answer:
No, it is not true statement as the angles should be included angle of there two given sides.
Question 3. In the given figure, AB=AC and AP=AQ. Prove that
(i) ∆APC ≅ ∆AQB
(ii) CP = BQ
(iii) ∠APC = ∠AQB.
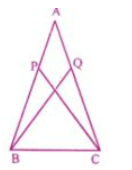
Answer:
(i) In △ APC and △AQB
AB=AC and AP=AQ [given]
From the given figure, ∠A = ∠A [common in both the triangles]
Therefore, using SAS axiom we have ∆APC ≅ ∆AQB
(ii) In △ APC and △AQB
AB=AC and AP=AQ [given]
From the given figure, ∠A = ∠A [common in both the triangles]
By using corresponding parts of congruent triangles concept we have
BQ = CP
(iii) In △ APC and △AQB
AB=AC and AP=AQ [given]
From the given figure, ∠A = ∠A [common in both the triangles]
By using corresponding parts of congruent triangles concept we have
∠APC = ∠AQB.
Question 4. In the given figure, AB = AC, P and Q are points on BA and CA respectively such that AP = AQ. Prove that
(i) ∆APC ≅ ∆AQB
(ii) CP = BQ
(iii) ∠ACP = ∠ABQ.
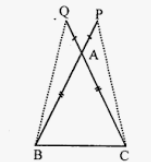
Answer:
(i) In the given figure AB = AC
P and Q are point on BA and CA produced respectively such that AP = AQ
Now we have to prove ∆APC ≅ ∆AQB
By using corresponding parts of congruent triangles concept we have
CP = BQ
∠ACP = ∠ABQ
(ii) CP = BQ
(iii) ∠ACP = ∠ABQ
In ∆ APC and ∆AQB
AC = AB (Given)
AP = AQ (Given)
∠PAC =∠QAB (Vertically opposite angle)
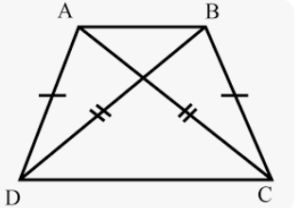
Question 5. In the given figure, AD = BC and BD = AC. Prove that :
∠ADB = ∠BCA and ∠DAB = ∠CBA.
Answer:
Given: in the figure, AD = BC, BD = AC

To prove :
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
Proof : in ∆ADB and ∆ACB
AB = AB (Common)
AD = BC (given)
DB = AC (Given)
∆ADB = ∆ACD (SSS axiom)
∠ADB = ∠BCA
∠DAB = ∠CBA
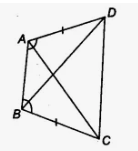
Question 6. In the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. Prove that
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
Answer:
Given : in the figure ABCD is a quadrilateral
In which AD = BC
∠DAB = ∠CBA
To prove :
(i) ∆ABD = ∆BAC
(ii) ∠ABD = ∠BAC
Proof : in ∆ABD and ∆ABC
AB = AB (common)
∠DAB = ∠CBA (Given)
AD = BC
(i) ∆ABD ≅ ∆ABC (SAS axiom)
(ii) BD = AC
(ii) ∠ABD = ∠BAC
Question 7.In the given figure, AB = DC and AB || DC. Prove that AD = BC.
Answer:
Given: in the given figure.
AB = DC, AB ∥ DC
To prove : AD = BC
Proof : AB ∥ DC
∠ABD = ∠CDB (Alternate angles)
In ∆ABD and ∆CDB
AB = DC
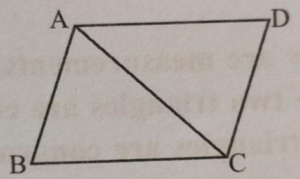
∠ABD = ∠CDB (Alternate angles)
BD = BD (common)
∆ABD ≅ CDB (SAS axiom)
AD = BC
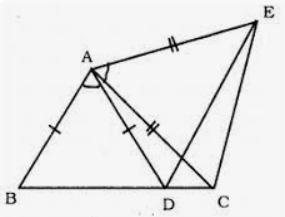
Question 8. In the given figure. AC = AE, AB = AD and ∠BAD = ∠CAE. Show that BC = DE.
Answer:
Given: in the figure, AC = AE, AB = AD
∠BAD = ∠CAE
To prove : BC = DE
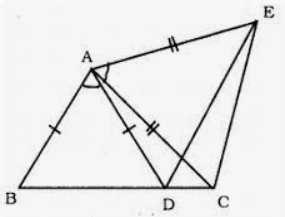
Proof : in ∆ABC and ∆ADE
AB = AD (given)
AC = AE (given)
∠BAD + ∠DAC + ∠CAE
∠BAC = ∠DAE
∆ABC = ∆ ADE (SAS axiom)
BC = DE
Question 9. In the adjoining figure, AB = CD, CE = BF and ∠ACE = ∠DBF. Prove that
(i) ∆ACE ≅ ∆DBF
(ii) AE = DF.
Answer:
Given : in the given figure
AB = CD
CE = BF
∠ACE = ∠DBF
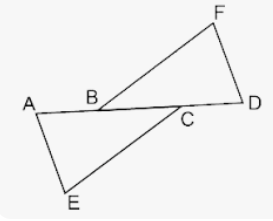
To prove : (i) ∆ACE ≅ ∆DBF
(i) ∆ACE ≅ ∆DBF (SAS axiom)
AE = DE
(ii) AE = DF
Proof : AB = CD
Adding BC to both sides
AB + BC = BC + CD
AC = BD
Now in ∆ACE and ∆DBF
AC = BD (Proved)
CE = BF (Given)
∠ACE = ∠DBF (SAS axiom)
Question 10. In the adjoining figure, AB = AC and D is mid-point of BC. Use SSS rule of congruency to show that
(i) ∆ABD ≅ ∆ACD
(ii) AD is bisector of ∠A
(iii) AD is perpendicular to BC
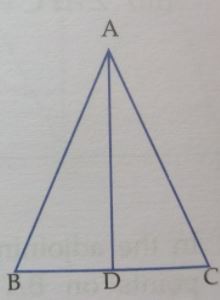
Answer:
We will use the SSS congruency rule to prove this.
In ∆ABD and ∆ACD,
AB=AC (given)
AD=AD (common)
BD=CD (given AD is the bisector)
So, ∆ABD is congruent to ∆ACD on SSS rule.
By CPCT, angle ADB = angle ADC
But BDC is a straight line, so angle ADB + angle ADC = 180°
Which implies angle ADB=90°
Question 11. Two line segment AB and CD bisect each other at O. Prove that
(i) AC = BD
(ii) ∠CAB = ∠ABD
(iii) AD || CB
(iv) AD = CB
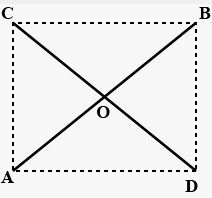
Answer:
AB and CD bisect each other at O i.e, AO=BO and CO=DO
in ΔCOA and ΔDOB
Given CO=OD,∠COA=∠BOD [ vertically opposite angles]
AD=BD
∴ΔCOA≅ΔBOD
(i) ∴AC=BD[C.P.CT]
(ii) ∠CAB=∠ABD[C.P.CT]
again
in ΔCOB and ΔAOD
CO=OD [given]
BO=AO [given]
∠COB=∠AOD [vertically opposite angles]
∴ΔCOB≅ΔAOD
∴∠CBA=∠BAD [ C.P. C.T]
(iii) As we know the quadrilateral whose diagonals bisect each other is a parallelogram…..
So ABCD is a parallelogram
THEN, AB || BC
(iv) and so AD||CD [ ∵∠CBA=∠BAD which are alternate angles]
and AD=CB [C.P.C.T]
Question 12. In the adjoining figure, find the value of and y.

Answer:
as two sides are equal ,35= 2x+5
2x =30
x=15
y+5=46
y=41
— : End of ML Aggarwal Triangles Exe-10.1 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends