Trigonometric Equations Class 11 OP Malhotra Exe-6A ISC Maths Solutions Ch-6 Solutions. In this article you would learn about Equations on sinθ, cosθ, tanθ, sin²θ, cos²θ and tan²θ. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Trigonometric Equations Class 11 OP Malhotra Exe-6A ISC Maths Solutions Ch-6
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-6 | Trigonometric Equations |
| Writer | OP Malhotra |
| Exe-6(A) | Equations on sinθ, cosθ, tanθ, sin²θ, cos²θ and tan²θ. |
Exercise- 6A
Trigonometric Equations Class 11 OP Malhotra Exe-6A Solution.
Que-1: Solve the following equations for 0 ≤ x ≤ 2π.
(i) 2 sin x – 1 = 0
(ii) sin x cos x = 0
(iii) tan θ + √3 = 0
(iv) sin θ cos θ = 1/2
(v) 2 sin² θ = 3 cos θ
(vi) 2 + 7 tan² θ = 3.25 sec² θ
Sol: (i) Given 2 sin x – 1 = θ
⇒ sin x = 1/2 = sin π/6
x = nπ+(-1)^n (π/6) where n ∈ I
when n = 0 then x = π/6
when n = 1 then x = π – (π/6) = 5π/6
When n = 2 then x = 2π + (π/6) ∉ [0,2π]
Hence x = π/6, 5π/6
(ii) sin x cos x = 0 ; 0 ≤ x ≤ 2π
⇒ (1/2) sin 2x = 0
⇒ sin 2x = 0
⇒ 2x = nπ
⇒ x = nπ/2; where n ∈ I
∴ x = 0, (π/2), π, (3π/2), 2π
(iii) Given tan θ + √3 = 0
⇒ tan θ = –√3 ; 0 ≤ θ ≤ 2π
⇒ tan θ = – tan (π/3) = tan(-π/3)
θ = nπ + (-π/3) ; where n ∈ I
For n = 0 ; θ = (-π/3) [0, 2π]
For n = 1 ; θ = π – (π/3) = 2π/3
For n = 2 ; θ = 2π – (π/3) = 5π/3
Thus, θ = 2π/3, 5π/3 ∈ [0, 2π]
(iv) sin θ cos θ = 1/2
⇒ 2 sin θ cos θ = 1
⇒ sin 2θ = 1 = sin π/2
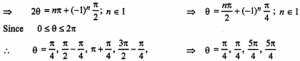
θ = π/4, 5π/4 ∈ [0, 2π]
(v) 2 sin² θ = 3 cos θ
We know that,
sin2θ = 1 – cos2θ
Given that,
2sin2θ = 3 cosθ
2 – 2cos2θ = 3cosθ
2cos2θ + 3cosθ – 2 = 0
(cosθ + 2)(2cosθ – 1) = 0
Therefore,
cosθ = 1/2 = cos π/3
θ = π/3 or 2π – (π/3)
θ = π/3, 5π/3
Therefore, 2(1 – cos2θ) = 3cosθ
⇒ 2 – 2cos2θ = 3cosθ
⇒ 2cos2θ + 3cosθ – 2 = 0
⇒ 2cos2θ + 4cosθ – cosθ – 2 = 0
⇒ 2cosθ(cosθ + 2) + 1(cosθ + 2) = 0
⇒ (2cosθ + 1)(cosθ + 2) = 0
Since, cosθ ∈ [–1, 1], for any value θ.
So, cosθ ≠ –2
Therefore,
2cosθ – 1 = 0
⇒ cosθ = 1/2
= π/3 or 2π – (π/3)
θ = π/3, 5π/3
(vi) 2 + 7 tan² θ = 3.25 sec² θ
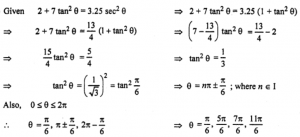
Que-2: cos θ + sin θ – sin 2θ = 1/2, 0 < θ < π/2
Sol: Given sin θ + cos θ – sin 2θ = 1/2, 0 < θ < π/2
⇒ 2 (sin θ + cos θ) = 1 + sin 2θ
On squaring both sides ; we have
4 (sin θ + cos θ)² = (1 + 2 sin 2θ)²
⇒ 4 [sin² θ + cos² θ + sin 2θ] = [1 + 4 sin² 2θ + 4 sin 2θ]
⇒ 4 [1 + sin 2θ] = 1 + 4 sin² 2θ + 4 sin 2θ ⇒ 4 sin² 2θ = 3
sin² 2θ = {√3/2}² = sin² π/3
2θ = nπ ± (π/3) = θ = nπ/2 ± π/6 where n ∈ I
For n = 0 ; θ = π/6
For n = 1 ; θ = (π/2) – (π/6) = π/3
Hence, θ = π/6, π/3
Que-3: sin 5θ = cos 2θ, 0° < θ < 180°.
Sol: Given : sin 5θ = cos 2θ, 0° < θ < 180°.
sin 5θ = sin [π/2 – 2θ]
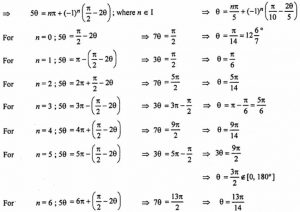
sin x + cos (x + 30°) = 0, 0° < x < 360°.
Que-4: cot²θ – (1 + √3)cot θ + √3 = 0, 0 < θ < π/2
Sol: Given cot²θ – (1 + √3)cot θ + √3 = 0, 0 < θ < π/2
⇒ cot²θ – cot θ – √3 cot θ + √3 = 0
⇒ cot θ (cot θ – 1) – √3 (cot θ – 1) = 0
⇒ (cot θ – 1) (cot θ – √3) = 0
⇒ cot θ – 1 = 0 or cot θ – √3 = 0
⇒ tan θ = 1 or tan θ = 1/√3
⇒ θ = π/4 or θ = π/6
Since 0 < θ < π/2
∴ θ = π/4, π/6
Que-5: sin x + cos (x + 30°) = 0, 0° < x < 360°.
Sol: Given : sin x + cos (x + 30°) = 0, 0° < x < 360°.
sin x = -cos (x+30°)
sin x = sin [(3π/2) – (x+30°)]
sin = nx + (-1)^n {(3π/2) – x – 30°} ; n ∈ I
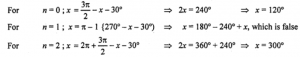
x = 120°, 300°
Que-6: cos 6θ + cos 4θ + cos 2θ + 1 = 0, 0° < θ < 180°
Sol: Given : cos 6θ + cos 4θ + cos 2θ + 1 = 0
cos6θ + cos4θ = 2cos((6θ+4θ)/2) cos((6θ−4θ)/2)
2cos(5θ) cos(θ)
2cos (5θ) cos (θ) + cos 2θ + 1 = 0
2cos (5θ) cos (θ) + (2cos²θ−1) + 1 = 0
2cos (5θ) cos (θ) + 2cos²θ = 0
2cos θ (cos(5θ) + cosθ) = 0
cosθ = 0 ⟹ θ = 90°
cos (5θ) + cos θ = 0
⟹ 2cos{(5θ+θ)/2} cos{(5θ−θ)/2} = 0
cos(3θ) = 0 :
3θ = 90° + n⋅180°
⟹ θ = 30° + n⋅60°
For n = 0 : θ = 30°
For n = 1 : θ = 90°
For n = 2 : θ = 150°
cos(2θ) = 0 :
2θ = 90° + n⋅180°
⟹ θ = 45° + n⋅90°
For n = 0 : θ = 45°
For n = 1 : θ = 135°
From cosθ = 0 : θ = 90°
From cos(3θ) = 0 : θ = 30°, 90°, 150°
From cos(2θ) = 0 : θ = 45°, 135°
Thus, the complete set of solutions in the interval 0° < θ < 180° is:
θ = 30°, 45°, 90°, 135°, 150°
Que-7: sin 7θ + sin 4θ + sin θ = 0, 0 < θ < π/2
Sol: Given : sin 7θ + sin 4θ + sin θ = 0, 0 < θ < π/2
(sin 7θ + sin θ) + sin 4θ = 0
2sin [(7θ+θ)/2] cos [(7θ-θ)/2] + sin 4θ = 0
2sin 4θ cos 3θ + sin 4θ = 0
sin 4θ [2cos 3θ + 1] = 0
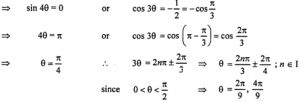
Thus, θ = (π/4), (2π/9), (4π/9)
Solve, giving the general value.
Que-8: 2 cos² θ – 5 cos θ + 2 = 0
Sol: 2 cos² θ – 5 cos θ + 2 = 0
⇒ cos θ = [5±√(25−16)/4] = (5±3)/4 = 2, 1/2
since |cos θ | ≤ 1 ∴ cos θ = 1/2 = cos π/3
⇒ θ = 2nπ ± π/3; where n ∈ I
which gives the required general soln.
Que-9: 2 sin² x + √3 cos x + 1 = 0
Sol: 2sin²x + √3 cos x + 1 = 0
⇒ 2 − 2cos²x + √3 cos x + 1 = 0
⇒ 2cos²x − √3 cos x − 3 = 0
⇒ 2cos²x − 2√3 cos x + √3 cos x − 3 = 0
⇒ 2cosx (cosx−√3) + √3 (cosx−√3) = 0
⇒ (2cosx+√3) (cosx−√3) = 0
⇒ (2cosx+√3) = 0 or
(cosx−√3) = 0
cos x = √3 is not possible.
∴ 2cosx + √3 = 0
⇒ cos x = −√3/2
⇒ cos x = cos(5π/6)
⇒ x = 2nπ ± (5π/6)
Que-10: 2 + √3sec x – 4cos x = 2√3
Sol: Given : 2 + √3sec x – 4cos x = 2√3
(√3/cos x) – 4 cos x = 2√3 – 2
4 cos²x + (2√3-2) cos x – √3 = 0
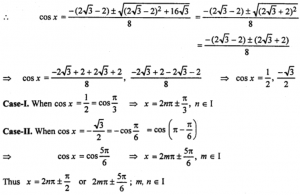
Que-11: tan² θ – (1 + √3)tan θ + √3 = 0
Sol: Given tan² θ – (1 + √3)tan θ + √3 = 0
⇒ tan θ (tan θ – 1) – √3 (tan θ – 1) = 0
⇒ (tan θ – 1) (tan θ – √3) = 0
⇒ tan θ = 1 or tan θ = √3
∴ tan θ = (π/4) or tan θ = tan (π/3)
⇒ θ = nπ + (π/4) or θ = mπ + (π/3)
∴ θ = nπ + (π/4) or mπ + (π/3) where m, n ∈ I
Que-12: tan θ + 4 cot 2θ + 1 = 0
Sol: Given tan θ + 4 cot 2θ + 1 = 0
⇒ [tan θ + 4(1−tan2θ)]/2tanθ + 1 = 0
⇒ 2 tan² θ + 4 – 4 tan² θ + 2 tan θ = 0
⇒ 2 tan² θ – 2 tan θ – 4 = 0
⇒ tan² θ – tan θ – 2 = 0
⇒ tan θ = [−(−1)±√(1+8)]/2 = (1±3)/2 = 2, – 1
Case-I. When tan θ = 2 ⇒ tan θ = tan α ⇒ θ = nπ + α, where α = tan‾¹ 2
Case-II. When tan θ = – 1 = – tan (π/4) = tan(-π/4) ⇒ θ = mπ – π/4 ; m ∈ I
Thus, θ = mπ – π/4, nπ + α ; where m, n ∈ I
Que-13: tan θ + tan² θ + √3 tan θ tan 2θ = √3
Sol: Given : tan θ + tan² θ + √3 tan θ tan 2θ = √3
tan θ + tan 2θ = √3 (1-tanθ tan2θ)
(tanθ + tan2θ)/(1-tanθ tan2θ) = √3
tan (θ+2θ) = √3
tan 3θ = √3 = tan π/3
3θ = nπ + (π/3) ; where n ∈ I
θ = nπ/3 + π/9; where n ∈ I
Que-14: cot θ + tan θ = 2 cosec θ
Sol: Given cot θ + tan θ = 2 cosec θ … (1)
⇒ (cosθ/sinθ) + (sinθ/cosθ) = 2 sinθ
⇒ (cos²θ+sin²θ)/cosθ sinθ = 2sinθ
⇒ 2/sin2θ = 2sinθ
⇒ sin 2θ = sin θ
⇒ sin θ (2 cos θ – 1) = 0
But sin θ ≠ 0 otherwise eqn. (1) is not possible.
∴ 2 cos θ – 1 = 0
⇒ cos θ = 1/2 = cos (π/3)
⇒ θ = 2nπ ± (π/3), where n ∈ I
Que-15: 2 cos θ + cos 3θ = 0
Sol: Given : 2 cos θ + cos 3θ = 0
2cos θ + [4cos³ θ – 3cos θ] = 0
cos θ [2 + 4cos² θ – 3] = 0
cos θ [4cos² θ – 1] = 0
cos θ = 0
θ = nπ + π/2
cos² θ = (1/2)² = cos² π/3
θ = mπ ± π/3
θ = nπ + π/2, mπ ± π/3, where m, n ∈ I
Que-16: 2 sin 2x – sin x = 0
Sol: Given : 2 sin 2x – sin x = 0
4 sin x cos x – sin x = 0
sin x (4 cos x – 1) = 0
sin x = 0
x = nπ, n ∈ I
4 cos x – 1 = 0
cos x = 1/4 cos α
x = 2nπ ± α, where α = cos¯¹ = 1/4
x = nπ, 2nπ ± α, where n ∈ I
Que-17: tan 2x + 2 tan x = 0
Sol: Given : tan 2x + 2 tan x = 0
2 tan x/1-tan²x + 2 tan x = 0
{2 tan x/1-tan²x} [1 + 1 – tan²x] = 0
tan x = 0 or tan²x = 2 = tan²α where tan²x ≠ 1
x = nπ
x = nπ ± α, n ∈ I
and tan²x ≠ 1 = tan² π/4
x ≠ nπ + π/4
x = nπ, nπ ± α – {nπ + π/4}; where n ∈ I and tan²α = 2.
Que-18: sin 7θ + sin 4θ + sin θ = 0
Sol: Given : sin 7θ + sin 4θ + sin θ = 0
sin 7θ + sin θ + sin 4θ = 0
2sin {(7θ+θ)/2} cos {(7θ-θ)/2} + sin 4θ = 0
2 sin 4θ cos 3θ + sin 4θ = 0
sin 4θ (2 cos 3θ + 1) = 0
sin 4θ = 0 or 2 cos 3θ + 1 = 0
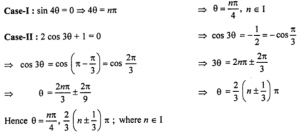
Que-19: cos θ + cos 2θ + cos 3θ = 0
Sol: cosθ + cos2θ + cos3θ = 0
or (cosθ + cos3θ) + cos2θ = 0
or 2cos θ cos 2θ + cos 2θ = 0
or cos 2θ (2cos θ + 1) = 0
or cos 2θ = 0 or 2cos θ + 1 = 0
⇒ 2θ = (2n+1) (π/2) or cos θ = −1/2, n ∈ Z
or θ = (2n+1) (π/4) or θ = 2nπ ± (2π/3), ∀ n ∈ Z
Que-20: sin θ + cos θ = √2.
Sol: Given : sin θ + cos θ = √2.
(1/√2) sin θ + (1/√2) cos θ = 1
sin θ sin (π/4) + cos (π/4) cos θ = 1
cos [θ – (π/4)] = 1 = cos 0
θ – (π/4) = 2nπ ± 0
θ = 2nπ + (π/4) where n ∈ I
Que-21: sin θ + √3 cos θ = √2
Sol: Given sin θ + √3 cos θ = √2
⇒ (1/2) sin θ + (√3/2) cos θ = 1/√2
⇒ sin θ cos (π/3) + cos θ sin (π/3) = sin (π/4)
⇒ sin (θ + (π/3)) = sin π/4
⇒ θ + (π/3) = nπ + (-1)n (π/4)
⇒ θ = nπ – (π/3) + (-1)n (π/4), where n ∈ I
Que-22: √2 sec θ + tan θ = 1
Sol: Given that,
√2 sec θ + tan θ = 1
√2 cos θ + (sinθ/cosθ) = 1
⇒ √2 + sin θ = cos θ
⇒ cos θ − sin θ = √2
Dividing by √2
⇒ (1/√2) cosθ − (1/√2) sinθ = 1
⇒ cos (θ+(π/4)) = cos 0
⇒ θ + (π/4) = 2nπ ± 0
⇒ θ = 2nπ − (π/4), n ∈ I
Que-23: 3 – 2 cos θ – 4 sin θ – cos 2θ + sin 2θ = 0
Sol: Given 3 – 2 cos θ – 4 sin θ – cos 2θ + sin 2θ = 0
⇒ 3 – 2 cos θ – 4 sin θ – (1 – 2 sin² θ) + 2 sin θ cos θ = 0
⇒ 2 – 2 cos θ – 4 sin θ + 2 sin² θ + 2 sin θ cos θ = 0
⇒ 1 – cos θ – 2 sin θ + sin² θ + sin θ cos θ = 0
⇒ 1 – cos θ – sin θ – sin θ + sin² θ + sin θ cos θ = 0
⇒ (1 – sin θ) – cos θ(1 – sin θ) – sin θ(1 – sin θ) = 0
⇒ (1 – sin θ) (1 – cos θ – sin θ) = 0
∴ 1 – sin θ = 0 or 1 – cos θ – sin θ = 0
Case-I:
1 – sin θ = 0 ⇒ sin θ = 1 = sin π/2
⇒ θ = nπ + (-1)^n (π/2) ; n ∈ I
Case-II:
1 – cos θ – sin θ = 0
⇒ cos θ + sin θ = 1
⇒ (1/√2) cos θ + (1/√2) sin θ = 1/√2
⇒ cos θ cos (π/4) + sin θ sin (π/4) = 1/√2
⇒ cos (θ−(π/4)) = 1√2 = cos π/4
⇒ θ – π/4 = 2nπ ± π/4
⇒ θ = 2nπ ± π/4 + π/4
⇒ θ = 2nπ, 2nπ ± π/2
Hence general soln. is given by θ = nπ + (-1)^n, 2nπ, 2rm + π/2, n ∈ I
Que-24: If the equation a cos 2θ + b sin 2θ = c has θ1, θ2 as its roots, prove that
(i) tan θ1 + tan θ2 = 2b/(c+a)
(i) tan θ1.tan θ2 = (c−a)/(c+a)
Sol: (i) Given
a cos θ + b sin 2θ = c … (1)
⇒ [a(1−tan²θ)]/(1+tan²θ) + [b{(2tanθ)/(1+tan2θ)}] = c
⇒ a (1 – tan² θ) + 2b tan θ = c (1 + tan² 0)
⇒ (a + c) tan² θ – 2b tan θ + c – a = 0 … (2)
since it is given that θ1, θ2 are the roots of eqn. (1)
∴ tan θ1 and tan θ2 are the roots of eqn. (2)
∴ tan θ1 + tan θ2 = sum of roots = – (−2b)/(a+c) = 2b/(a+c)
(ii) product of roots = tan θ1 tan θ2 = (c−a)/(c+a)
Que-25: If α, ß are two different values of θ lying between 0 and 2π which satisfy the equation 6 cos θ + 8 sin θ = 9, find the value of sin (α + ß).
Sol: Given:
6 cosx + 8 sinx = 9
⇒ 6 cos x = 9 – 8 sin x
⇒ 36 cos2x = (9 – 8 sinx)2
⇒ 36(1 – sin2x) = 81 + 64 sin2x – 144 sinx
⇒100 sin2x – 144 sinx + 45 = 0
Now, α and β are the roots of the given equation; therefore, cos α and cos β are the roots of the above equation.
⇒ sinα sinβ = 45/100 (Product of roots of a quadratic equation ax²+bx+c = 0 is c/a.)
Again, 6 cosx + 8 sinx = 9
⇒ 8 sinx = 9 – 6 cosx
⇒ 64 sin2x = (9 – 6 cosx)2
⇒ 64(1 – cos2x) = 81 + 36cos2x – 108 cosx
⇒ 100 cos2x – 108 cosx + 17 = 0
Now, α and β are the roots of the given equation; therefore, sin α and sin β are the roots of the above equation.
Therefore, cos α cos β = 17/100
Hence, cos(α + β) = cos α cos β – sin α sin β
= (17/100) – (45/100)
= -28/100
= -7/25
sin(α+β) = √[1−cos²(α+β)]
= √[1−(−7/25)²]
= √(576/625)
= 24/25
Que-26: Find all the values of θ satisfying the equation cos 2θ – cos 8θ + cos 6θ = 1, such that 0 ≤ θ ≤ n.
Sol: Given : cos 2θ – cos 8θ + cos 6θ – 1 = 0
(cos 6θ + cos 2θ) – (1 + cos 8θ) = 0
2 cos {(6θ+2θ)/2} cos {(6θ-2θ)/2} – 2 cos² 4θ = 0
2 cos 4θ cos 2θ – 2 cos² 4θ = 0
2 cos 4θ [cos 2θ – cos 4θ] = 0
2 cos 4θ [2 sin {(2θ+4θ)/2} sin {(4θ-2θ)/2}] = 0
cos 4θ sin 3θ sin θ = 0
cos 4θ = 0 or sin 3θ = 0 or sin θ = 0
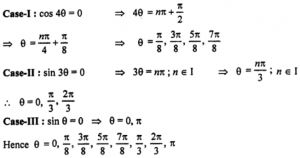
Que-27: sec θ – cosec θ = 4/3
Sol: Given : sec θ – cosec θ = 4/3
(1/cos θ) – (1/sin θ) = 4/3
3 (sinθ – cosθ) = 4 sinθ cosθ
3 (sinθ – cosθ) = 2 sin 2θ
On squaring both sides we have
9 [sin²θ + cos²θ – 2 sinθ cosθ] = 4 sin² 2θ
9 [1 – sin 2θ] = 4 sin² 2θ
4 sin² 2θ + 9 sin 2θ – 9 = 0

Que-28: Find the smallest positive number p for which the equation cos (p sin x) = sin (p cos x) has a solution when x ∈ [0, 2π].
Sol: Given cos (p sin x) = sin (p cos x) x ∈ [0, π]
cos (p sin x) = sin (p cos x)
sin (π/2 – p sin x) = sin (p cos x)
π/2 – p sin x = p cos x
p(sin x + cos x)= π/2
p = π/2/(sinx + cosx)
So, to minimize p, sin x + cos x must be maximized.
sin x + cos x = √2sin (x + π/4) , which is maximized when sin(x + π/4) = 1 at x = π/4.
p√2(sin(x + π/4)) = π/2
p = π/2 / √2sin(π/2)
= π/2√2.
–: End Trigonometric Equations Class 11 OP Malhotra Exe-6A ISC Math Ch-6 Solution :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends