ML Aggarwal Trigonometric Identities Exe-18 Solutions ICSE Class-10 Maths Ch-18. We Provide Step by Step Answer of Exercise-18 Trigonometric Identities Questions for ICSE Class-10 APC Understanding Mathematics. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Trigonometric Identities Exe-18 Solutions ICSE Class-10 Maths Ch-18
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-18 | Trigonometric Identities |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-18 |
| Academic Session | 2024-2025 |
ML Aggarwal Trigonometric Identities Exe-18 Solutions
ICSE Class-10 Maths Ch-18
Question 1. If A is an acute angle and sin A = 3/5 find all other trigonometric ratios of angle A (using trigonometric identities).
Answer :
sin A = 3/5
In ∆ABC, ∠B = 90°
AC = 5 and BC = 3
By Pythagoras theorem,
AB = √(AC2 – BC2)
= √(52 – 32) = √(25 – 9)
= √16
= 4
Now,
cos A = AB/AC = 4/5
tan A = BC/AB = 3/4
cot A = 1/tan θ = 4/3
sec A = 1/cos θ = 5/4
cosec A = 1/sin θ = 5/3
Question 2. If A is an acute angle and sec A = 17/8, find all other trigonometric ratios of angle A (using trigonometric identities).
Answer :
sec A = 17/8 (A is an acute angle)
In right ∆ABC
sec A = AC/AB = 17/8
AC = 17, AB = 8
By Pythagoras theorem,
BC = √(AC2 – AB2)
= √(172 – 82) = √(289 – 64) = √225
= 15
Now,
sin A = BC/AC = 15/17
cos A = 1/sec A = 8/17
tan A = BC/AB = 15/8
cot A = 1/tan A= 8/15
cosec A = 1/sin A = 17/15
Question 3. If 12 cosec θ = 13, find the value of (2sinθ-3cosθ)/(4sinθ-9cosθ)
Answer :
12 cosec θ = 13
⇒ cosec θ = 13/12
In right ∆ABC,
∠A = θ
cosec θ = AC/AB = 13/12
AC = 13 and BC = 12
By Pythagoras theorem,
AB = √(AC2 – BC2)
= √[(13)2 – (12)2]
= √(169 – 144)
= √25
= 5
Now,
sin θ = BC/AC = 12/13
cos θ = AB/AC = 5/13
Hence,
(2sin θ – 3cos θ)/(4sin θ – 9 cos θ)
= (2 × 12/13 – 3 × 5/13)/(4 × 12/13 – 9 × 5/13)
= (24/13 – 15/13)/(48/13 – 45/13)
= 9/13 ÷ 3/13
= 9/13 × 13/3
= 3
Without using trigonometric tables, evaluate the following (6 to 10) :
Question 4.
(i) cos226o+ cos 64o sin 26o + (tan 36o/cot 54o)
(ii) (sec 17o/ cosec 73o) + (tan 68o/ cot 22o) + cos2 44o + cos2 46o
Answer :
Given that:
(i) cos2 26o + cos 64o sin 26o + (tan 36o/cot 54o)
= cos2 26o + cos (90o – 16o) sin 26o + [tan 36o/cot (90o – 54o)]
= [cos2 26o + sin2 26o] + (tan 36o/tan 36o)
= 1 + 1 = 2
(ii) (sec 17o/cosec 73o) + (tan 68o/cot 22o) + cos2 44o + cos2 46o
= [sec 17o/cosec (90o – 73o)] + [(tan 90o – 22o)/cot 22o] + cos2 (90o – 44o) + cos2 46o
= [sec 17o/sec 17o] + [cot 22o/cot 22o] + [sin2 46o + cos2 46o]
= 1 + 1 + 1
= 3
Question 5.
(i) (sin 65o/cos 25o) + (cos 32o/sin 58o) – sin 28osec 62o+ cosec2 30o
(ii) (sin 29o/ cosec 61o) + 2 cot 8° cot 17° cot 45° cot 73° cot 82° – 3(sin² 38° + sin² 52°).
Answer :
given that
Given,
(i) (sin 65o/cos 25o) + (cos 32o/sin 58o) – sin 28o sec 62o + cosec2 30o
= (sin 65o/cos (90o – 65o)) + (cos 32o/sin (90o – 32o)) – sin 28o sec (90o – 28o) + 22
= (sin 65o/sin 65o)+ (cos 32o/cos 32o) – [sin 28o x cosec 28o] + 4
= 1 + 1 – 1 + 4
= 5
(ii) (sin 29o/cosec 61o) + 2 cot 8° cot 17° cot 45° cot 73° cot 82° – 3(sin² 38° + sin² 52°).
= (sin 29o/cosec (90o – 29o)) + [2 cot 8° cot 17° cot 45° cot (90° – 17o) cot (90o – 8o)] – 3(sin² 38° + sin² (90° – 38o))
= (sin 29o/sin 29o) + [2 cot 8° cot 17° cot 45° tan 17o tan 8o] – 3(sin² 38° + cos² 38°)
= 1 + 2[(cot 8° tan 8o) (cot 17° tan 17o) cot 45°] – 3(1)
= 1 + 2[1×1×1] – 3
= 1 + 2 – 3
= 0
Question 6.
(i) (sin 35ocos 55o+ cos 35o sin 55 o)/ (cosec2 10o – tan2 80 o)
(ii) sin2 34o + sin2 56o + 2 tan18o tan 72o – cot2 30o
Answer :
Given that:
(i) (sin 35o cos 55o + cos 35o sin 55o)/ (cosec2 10o – tan2 80o)
= sin 35o cos (90o – 35o) + cos 35o sin (90o – 35o)/(cosec2 10o – tan2(90o – 10o)
= sin 35o sin 35o + cos 35o cos 35o)/(cosec2 10o – cot2 10o)
= (sin2 35o + cos2 35o)/(cosec2 10o – cot2 10o)
= 1/1
= 1
(ii) sin2 34o + sin2 56o + 2 tan18o tan 72o – cot2 30o
= sin2 34o + sin2 (90o – 34o) + 2 tan18o tan (90o – 18o) – cot2 30o
= [sin2 34o + cos2 34o] + 2 tan18o cot 18o – cot2 30o
= 1 + 2 x 1 – (√3)2
= 1 + 2 – 3
= 0
Question 7.
(i) (tan 25o/cosec 65o)2+ (cot 25o/sec 65o)2+ 2 tan 18o tan 45o tan 75o
(ii) (cos2 25o + cos2 65o) + cosec θ sec (90o – θ) – cot θ tan (90o – θ)
Answer :
(i) (tan 25o/ cosec 65o)2 + (cot 25o/ sec 65o)2 + 2 tan 18o tan 45o tan 75o
(ii) (cos2 25o + cos2 65o) + cosec θ sec (90o – θ) – cot θ tan (90o – θ)
= cos2 25o + cos2 (90o – 25o) + cosec θ sec (90o – θ) – cot θ. cot θ
= (cos2 25o + sin2 25o) + (cosec2 θ – cot2 θ)
= 1 + 1 = 2
Prove that following (12 to 30) identities, where the angles involved are acute angles for which the trigonometric ratios as defined:
Question 8.
(i) (sec A + tan A) (1 – sin A) = cos A
(ii) (1 + tan2 A) (1 – sin A) (1 + sin A) = 1.
Answer :
(i) (sec A + tan A) (1 – sin A) = cos A
L.H.S. = (sec A + tan A) (1 – sin A)
Question 9.
(i) tan A + cot A = sec A cosec A
(ii) (1 – cos A)(1 + sec A) = tan A sin A.
Answer :
(i) L.H.S. = tan A + cot A
= sin A/cos A + cos A/sin A
= (sin2 A + cos2 A)/(sin A cos A)
= 1/(sin A cos A)
= sec A cosec A
= R.H.S
(ii) L.H.S. = (1 – cos A) (1 + sec A)
= (1 – cos A)(1 + 1/cos A)
= (1 – cos A)(cos A + 1)/cos A
= (1 – cos2 A)/(cos A)
= (sin2A)/(cos A)
= sin2 A/cos A
= sin A × sin A/cos A {1 – cos2 A = sin2 A}
= tan A sin A
= R.H.S.
Question 10.
(i) cot² A – cos² A = cot² A cos² A
(ii) 1 + tan²A/ 1 + sec A = sec A
(iii) (1 + sec A)/ sec A = sin² A/ 1- cos A
(iv) sin A/(1 – cos A) = cosec A + cot A.
Answer :
(i) LHS = cot2 A – cos2 A
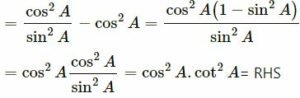
(ii) 1 + tan²A/ 1 + sec A = sec A
We know that tan² 2A + 1 = sec² 2A
tan² 2A = sec² 2A – 1
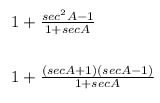
1 + sec A – 1
= sec A.
L.H.S = R.H.S.
(iii) (1 + sec A)/ sec A = sin² A/ 1- cos A
LHS = ( 1 + sec A )/sec A
= ( 1 + 1/cos A ) / ( 1/cosA )
= [ ( Cos A + 1 ) / cos A ] / ( 1/ cos A )
= Cos A + 1
= ( 1 + cos A ) ( 1 – cos A ) / ( 1 – cos A )
= ( 1 – cos² A ) / ( 1 – cos A )
= Sin² A / ( 1 – cos A )
= RHS
(iv) sin A/(1 – cos A) = cosec A + cot A.
If A = = θ
then,
We know that sin² θ = cos² θ = 1
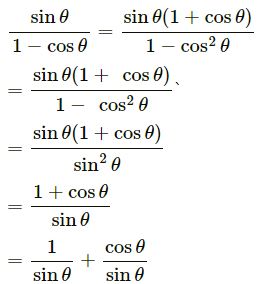
= cosec θ + cot θ.
= cosec A + cot A.
Question 11.
(i) sin A/ (1 + cos A) = (1 – cos A)/ sin A
(ii) (1 – tan2 A)/ (cot2 A – 1) = tan2 A
(iii) sin A/ (1 + cos A) = cosec A – cot A
Answer :
(i) sin A/ (1 + cos A) = (1 – cos A)/ sin A
L.H.S = sin A/ (1 + cos A)
(multiplying and dividing by (1 – cosA))
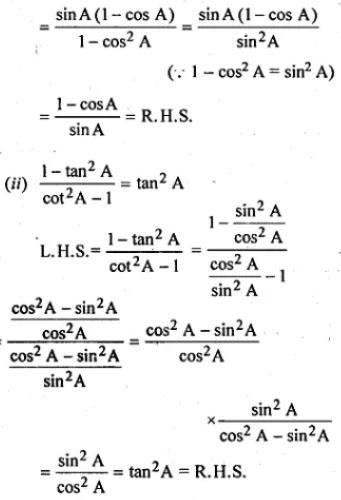
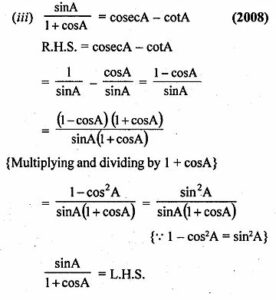
Question 12.
(i) (sec A – 1)/(sec A + 1) = (1 – cos A)/(1 + cos A)
(ii) tan2 θ/ (sec θ – 1)2 = (1 + cos θ)/ (1 – cos θ)
(iii) (1 + tan A)2 + (1 – tan A)2 = 2 sec2 A
(iv) sec2 A + cosec2 A = sec2 A. cosec2 A
Answer :
(i) (sec A – 1)/(sec A + 1) = (1 – cos A)/(1 + cos A)
L.H.S. = (sec A – 1)/(sec A + 1)
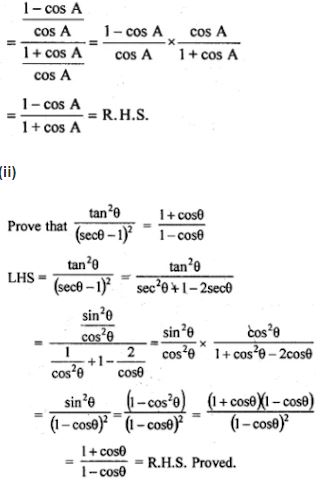
(iii) L.H.S. = (1 + tan A)2 + (1 – tan A)2
= 1 + 2 tan A + tan2 A + 1 – 2 tan A + tan2 A
= 2 + 2 tan2 A
= 2(1 + tan2 A) [As 1 + tan2 A = sec2 A]
= 2 sec2 A
= R.H.S.
(iv) L.H.S = sec2 A + cosec2 A
= 1/cos2 A + 1/sin2 A
= (sin2 A + cos2 A)/(sin2 A cos2 A)
= 1/ (sin2 A cos2 A)
= sec2 A cosec2 A = R.H.S
Question 13.
(i) (1 + sin A)/cos A + cos A/(1 + sin A) = 2 sec A
(ii) tan A/(sec A – 1) + tan A/(sec A + 1) = 2cosec A
Answer :
(i) L.H.S. = (1 + sin A)/cos A + cos A/(1 + sin A)
Question 14.
(i) cosec A/(cosec A – 1) + cosec A/(cosec A + 1) = 2 sec2A
(ii) cot A – tan A = (2cos2 A – 1)/ (sin A – cos A)
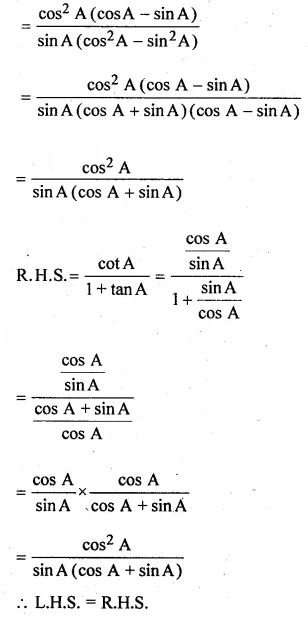
(iii) (cot A – 1)/ (2 – sec2 A) = cot A/ (1 + tan A)
Answer :
(i) L.H.S. = cosec A/(cosec A – 1) + cosec A/(cosec A + 1)
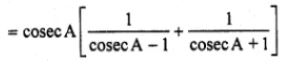
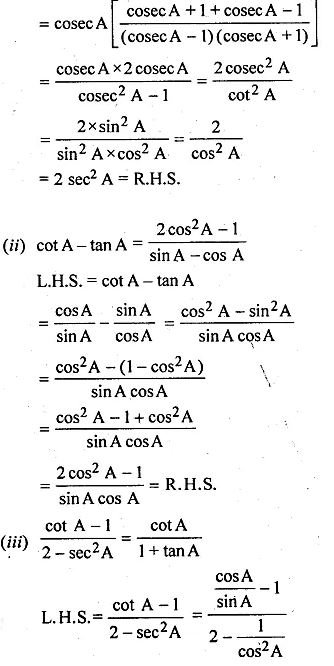
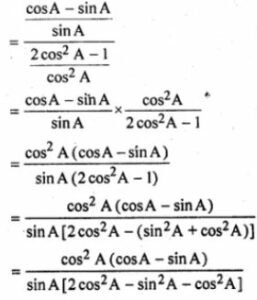
Question 15.
(ii) cos θ/ (1 – tan θ) – sin2 θ/ (cos θ – sin θ) = cos θ + sin θ
Answer :
(i) tan2θ – sin2θ = tan2 θ sin2 θ
L.H.S = tan2θ – sin2θ
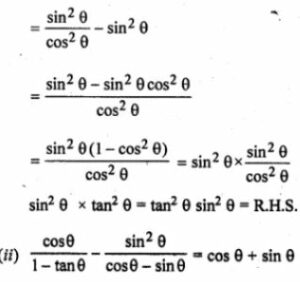
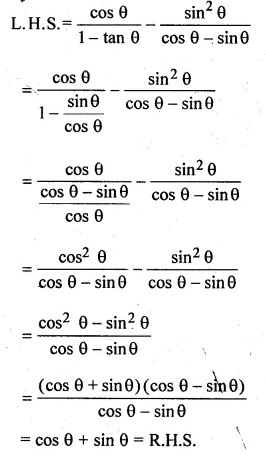
Question 16.
(i) cosec4 θ – cosec2 θ = cot4 θ + cot2 θ
(ii) 2 sec2 θ – sec4 θ – 2 cosec2 θ + cosec4 θ = cot4 θ – tan4 θ.
Answer :
(i) L.H.S. = cosec4 θ – cosec2 θ
= cosec2 θ (cosec2 θ – 1)
= cosec2 θ cot2 θ [cosec2 θ – 1 = cot2 θ]
= (cot2 θ + 1) cot2 θ
= cot4 θ + cot2 θ
= R.H.S.
(ii) L.H.S. = 2 sec2 θ – sec4 θ – 2 cosec2 θ + cosec4 θ
= 2 (tan2 θ + 1) – (tan2 θ + 1)2 – 2 (1 + cot2 θ) + (1 + cot2 θ)2
{∵ sec2 θ = tan2 θ + 1 cosec2 θ = 1 + cot2 θ}
= 2 tan2 θ + 2 – (tan4 θ + 2 tan2 θ + 1) – 2 – 2 cot2 θ + (1 + 2 cot2 θ + cot4 θ)
= 2 tan2 θ + 2 – tan4 θ – 2 tan2 θ – 1 – 2 – 2 cot2 θ + 1 + 2 cot2 θ + cot4 θ
= cot4 θ – tan4 θ = R.H.S.
Question 17.
(i) (1 + cos θ – sin2 θ)/(sin θ(1 + cos θ) = cot θ
(ii) (tan3 θ – 1)/(tan θ – 1) = sec2 θ + tan θ
Answer :
(i) (1 + cos θ – sin2 θ)/(sin θ(1 + cos θ) = cot θ
L.H.S = (1 + cos θ – sin2 θ)/(sin θ(1 + cos θ)
Question 18.
(i) (1 + cosec A)/cosec A = cos2 A/(1 – sin A)
(ii) √(1-cosA)/(1+cosA)=sinA/(1+cosA)
Answer :
(i) (1 + cosec A)/cosec A = cos2 A/(1 – sin A)
L.H.S = (1 + cosec A)/cosec A
Question 19.
(i) √(1+sinA)/(1-sinA)=tanA+secA
(ii) √(1-cosA)/(1+cosA)=cosecA-cotA
Answer :
(i) √(1+sinA)/(1-sinA)=tanA+secA
Question 20.
(i) √(secA-1)/(secA+1) +√(secA+1)/(secA-1)=2cosecA
(ii) cotA.cotA/(1-sinA)=(1+cosecA)
Answer :
(i) √(secA-1)/(secA+1) +√(secA+1)/(secA-1)=2cosecA
L.H.S = √(secA-1)/(secA+1) +√(secA+1)/(secA-1)
Question 21.
(i) (1 + tan A)/(sin A) + (1 + cot A)/cos A = 2(sec A + cosec A)
(ii) sec4 A – tan4 A = 1 + 2 tan2 A
Answer :
(i) (1 + tan A)/(sin A) + (1 + cot A)/cos A = 2(sec A + cosec A)
L.H.S = (1 + tan A)/(sin A) + (1 + cot A)/cos A
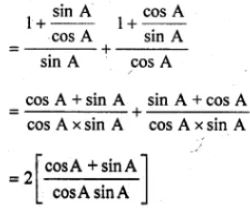
Question 22.
(i) cosec6 A – cot6 A = 3 cot2 A cosec2 A + 1
(ii) sec6 A – tan6 A = 1 + 3 tan2 A + 3 tan4 A
Answer :
(i) cosec6 A – cot6 A = 3 cot2 A cosec2 A + 1
L.H.S = cosec6 A – cot6 A
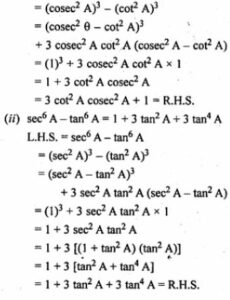
Question 23.
(i)( cotθ+cosecθ-1)/(cotθ-cosecθ+1)=(1+cosθ)/sinθ
(ii) sinθ/(cotθ+cosecθ)=2+[sinθ/(cotθ-cosecθ)]
Answer :
(i) (cot θ + cosec θ – 1)/(cot θ – cosec θ + 1) = (1 + cos θ)/sin θ
L.H.S. = (cot θ – cosec θ – 1)/(cot θ – cosec θ + 1)
(ii)
Question 24.
(i) (sinθ + cos θ)(secθ + cosecθ) = 2 + sec θ cosec θ
(ii) (cosec A – sin A) (sec A – cos A) sec2A = tan A
Answer :
(i) (sinθ + cosθ)(secθ + cosecθ) = 2 + secθ cosecθ
L.H.S = (sinθ + cosθ)(secθ + cosecθ)
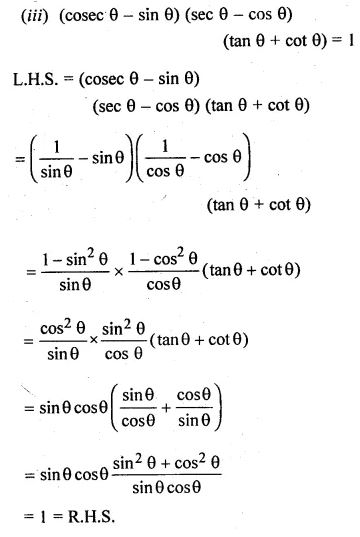
Question 25.
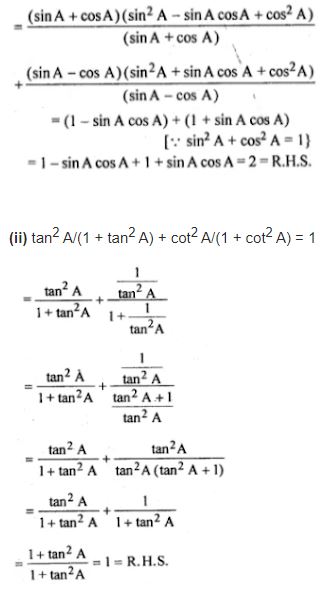
(i) (sin3 A + cos3 A)/(sin A + cos A) + (sin3 A – cos3 A)/(sin A – cos A) = 2
(ii) tan²A/(1+tan²A)+cot²A/(1+cot²A)=1
Answer :
(i) (sin3 A + cos3 A)/(sin A + cos A) + (sin3 A – cos3 A)/(sin A – cos A) = 2
L.H.S. = (sin3 A + cos3 A)/(sin A + cos A) + (sin3 A – cos3 A)/(sin A – cos A)
Question 26.
(i) 1/(secA+tanA)-1/cosA=1/cosA-1/(secA-tanA)
(ii)( sinA+secA)² + (cosA +cosecA)²=(1+secAcosecA)²
(iii) (tanA+sinA)/(tanA-sinA)=(secA+1)/(secA-1)
Answer :
(i) 1/(secA+tanA)-1/cosA=1/cosA-1/(secA-tanA)
L.H.S = 1/(secA+tanA)-1/cosA
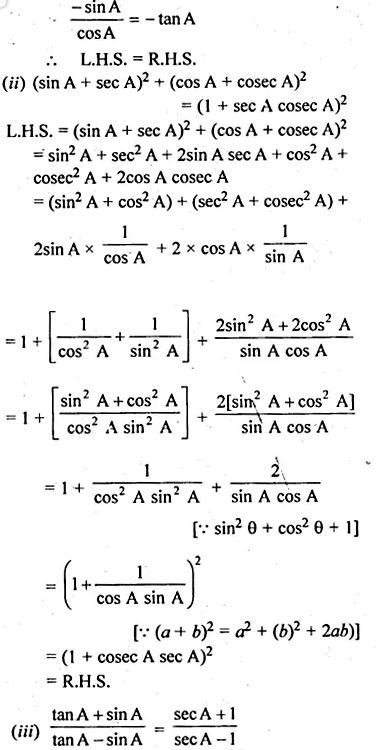
(ML Aggarwal Trigonometric Identities Exe-18 Solutions)
Question 27. If sin θ + cos θ = √2 sin (90° – θ), show that cot θ = √2 + 1
Answer :
sin θ + cos θ = √2 sin (90° – θ)
sin θ + cos θ = √2 cos θ
dividing by sin θ
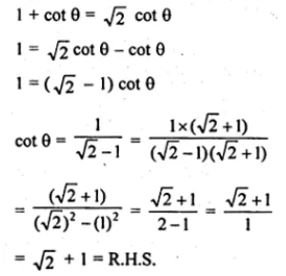
Question 28. If 7 sin2 θ + 3 cos2 θ = 4, 0° ≤ θ ≤ 90°, then find the value of θ.
Answer :
7 sin2 θ + 3 cos2 θ = 4, 0° ≤ θ ≤ 90°
3 sin2 θ + 3 cos2 θ + 4 sin2 θ = 4
⇒ 3 (sin2 θ + 3 cos2 θ) + 4 sin2 θ = 4
⇒ 3 (1) + 4 sin2 θ = 4
⇒ 4 sin2 θ = 4 – 3
⇒ sin2 θ = ¼
Taking square-root on both sides, we get
sin θ = ½
Thus, θ = 30o
Question 29. If sec θ + tan θ = m and sec θ – tan θ = n, prove that mn = 1.
Answer :
sec θ + tan θ = m and sec θ – tan θ = n
mn = (sec θ + tan θ) (sec θ – tan θ) = sec2 θ – tan2 θ = 1
(∴ sec2 θ – tan2 θ = 1)
Hence proved.
Question 30. If x – a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x2 – y2 = a2 – b2.
Answer :
x – a sec θ + b tan θ and y = a tan θ + b sec θ
To prove that x2 – y2 = a2 – b2.
= a2 sec2θ + b2 tan2θ + 2ab secθ tanθ – (a2 tan2θ + b2sec2θ + 2ab secθ tanθ)
= a2 sec2θ + b2tan2θ + 2ab secθ tanθ – a2tan2θ – b2sec2θ – 2ab secθ tanθ
= a2 (sec2θ – tan2θ) – b2 (sec2θ – tan2θ)
= a2 × 1 – b2 × 1 (sec2θ – tan2θ = 1)
= a2 – b2
Question 31. If x = h + a cos θ and y = k + a sin θ, prove that (x – h)2 + (y – k)2 = a2.
Answer :
x = h + a cos θ and y = k + a sin θ
To prove that (x – h)2 + (y – k)2 = a2.
x – h = a cos θ
y – k = a sin θ
On squaring and adding we get
(x – h)2 + (y – k)2 = a2 cos2 θ + a2 sin2 θ
= a2 (sin2 θ + cos2 θ)
= a2 (1) [Since, sin2 θ + cos2 θ = 1]
Hence, proved
{ sin² θ + cos² θ = 1}
— : End of ML Aggarwal Trigonometric Identities Exe-18 Solutions ICSE Class-10 Maths Ch-18 : –
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends
9 thoughts on “ML Aggarwal Trigonometric Identities Exe-18 Solutions ICSE Class-10 Maths Ch-18”
Number 11 sub part (iv) is missing
It has helped me a lot with my revision and today is Saturday and on Monday i have exam so thank you so much for this
Q 22(ii) question is different from the book in book it is sin a/1+cot a-cos a/1+tan a= sin a-cos a
Kindly do the changes and apply the solution for the same
update soon
In the Chapter : Trigonometric Identities, Excercise 18- Sum 23(i): The question displayed is wrong. The question displayed is-
(cotθ – cosecθ -1)÷(cotθ – cosecθ+1)=(1+cosθ)÷sinθ
The correct question is-(Both according to the book and the answer solved):
(cotθ + cosecθ -1)÷(cotθ – cosecθ+1)=(1+cosθ)÷sinθ
That is ,
In the L.H.S numerator, cosecθ is to be added instead of being subtracted. Meaning ,
(cotθ + cosecθ -1) instead of (cotθ – cosecθ -1).
There is no problem with the steps of the answer as it is solved according to the correct form of question.
Kindly solve this issue if possible.
Regards.
thanks for suggestion
now the problem has been solved correctly
This helped me a lot.
Tomorrow is my exam and now it’s 10.45 pm .
It helped me to do revision.
Thanks to the website owner.
🙂🙂
thanks for positive response
Due to you I can understand how to solve different types of problems