Trigonometrical Identities Concise Solutions Chapter-21 Class 10

Trigonometrical Identities Concise Solutions Chapter-21 Class 10. Selina  Concise Solutions of Exercise – 21 (A), Exercise – 21 (B), Exercise –21 (C), Exercise – 21 (D), Exercise –21 (E) for Class 10th. Concise Maths Solutions Trigonometrical Identities Chapter-21 for ICSE Maths Class 10 is available here. All Solutions of Concise Selina Maths of Trigonometrical Identities Chapter-21 has been solved according instruction given by council. This Post is the  Concise Solutions of Trigonometrical Identities Chapter-21 for ICSE Maths Class 10th.

Trigonometrical Identities Concise Solutions Chapter-21 Class 10

The Solutions of Concise Mathematics Trigonometrical Identities  Chapter-21 for ICSE Class 10. Experience teachers Solved Chapter-21 Trigonometrical Identities  of  Concise Selina Maths  for class 10th ICSE board. Therefore the ICSE Class 10th Maths Solutions of Concise Selina Publishers is helpful on  various topics including Chapter-21 Trigonometrical Identities.

–:Select Topic :–

Exercise – 21 (A),

Exercise – 21 (B),

Exercise –21 (C), 

Exercise – 21 (D),

Exercise – 21 (E),

EXERCISE -21(A) Trigonometrical Identities Concise Selina Maths Solutions for ICSE Class 10

Prove the following Identities :

Question 1.

…………

Answer 1

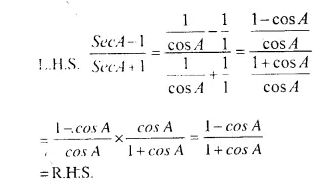
Question 2.

Answer 2

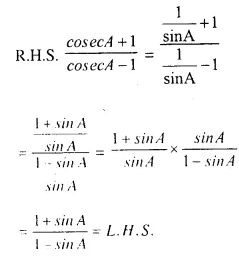
Question 3.

……….

Answer 3

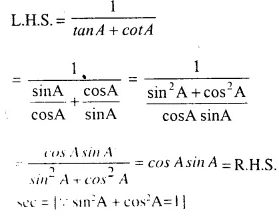
Question 4.

………..

Answer 4

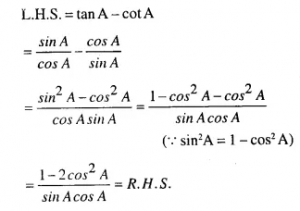
Question 5.

sin⁴A – cos⁴ A = 2 sin²A-1 

Answer 5

L.H.S. = sin⁴ A – cos⁴A = (sin²A)²-(cos²A)²
= (sin²A + cos²A) (sin²A – cos²A)     [(a² – b² = (a + b) (a – b)]
and = 1 (sin² A – cos²A) [∵ sin²A + cos²A = 1]
so = sin² A – (1- sin²A) (∵ cos²A = 1 – sin²A)
therefore = sin² A – 1 + sin² A
hence = 2 sin²A-1 = R.H.S.

Question 6.

(1 – tan A)² + (1 + tanA)² = 2sec²A

Answer 6

LHS = (1 -tanA)² + (1 +tanA)²
= 1 + tan² A- 2 tan A + 1 + tan² A + 2 tanA
and = 2 + 2 tan² A = 2 (1+tan²A)
hence = 2 sec²A (∵ l+tan²A=sec²A)
= R.H.S.

Question 7.

Cosec⁴ A – cosec² A = cot⁴ A + cot² A

Answer 7

L.H.S. = cosec⁴ A -cosec² A
= (cosec²A)² – cosec²A
and = (1 + cot²A)² – (1 + cot²A)
= 1 + cot⁴ A + 2 cot²A – 1- cot²A
hence = cot⁴ A + cot² A = R.H.S.

Question 8.

sec A (1-sin A) (sec A + tan A) = 1

Answer 8

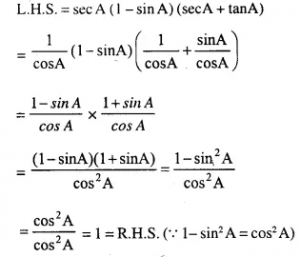
Question 9.

cosec A (1 + cos A) (cosec A – cot A) = 1

Answer 9

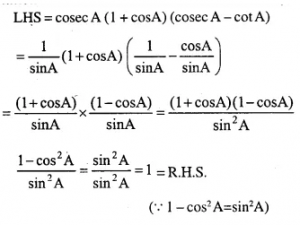
Question 10.

sec² A + cosec²A = sec² A cosec² A

Answer 10

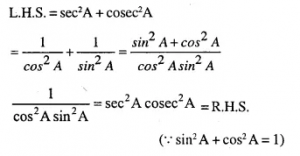
Question 11.

          …………

Answer 11

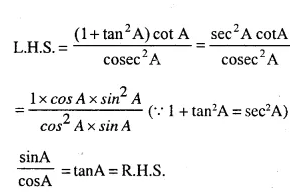
Question 12.

tan²A – sin²A = tan² A. sin² A

Answer 12

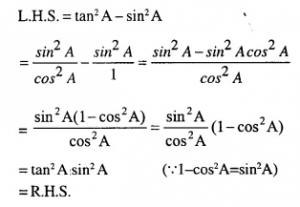
Question 13.

cot² A – cos² A = cos² A. cot² A

Answer 13

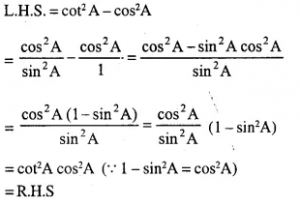
Question 14.

(cosecA + sinA) (cosec A – sinA) = cot² A + cos²A

Answer 14

L.H.S. = (cosec A + sin A) (cosec A – sin A)
= (cosec²A – sin² A) [∵ (a + b) (a – b) = a²– b²]
and = 1 + cot² A – sin² A = cot² A + 1 – sin²A
= cot² A + cos² A (∵ 1-sin²A = cos² A)
hence = R.H.S.

Question 15

(sec A – cosA) (sec A + cosA) = sin² A + tan²A

Answer 15

L.H.S. = (sec A-cos A) (sec A + cos A)
= sec² A – cos² A
and = 1 + tan²A-cos² A
= 1-cos² A + tan² A
so = sin² A + tan² A  (∵ 1- cos²A=sin²A)
hence = R.H.S.

Question 16.

(cos A + sin A)² + (cos A – sin A)² = 2

Answer 16

LHS = (cos A + sin A)² + (cos A – sin A)²
= cos² A + sin² A + 2 cos A sin A + cos² A + sin² A – 2 cos A sin A
and = 2 sin² A + 2 cos² A
= 2 (sin²A+cos²A)
hence = 2 x 1=2 = R.H.S. (∵ sin²A + cos² A = 1)

Question 17.

(cosec A – sinA) (sec A – cos A) (tan A + cot A) = 1

Answer 17

 

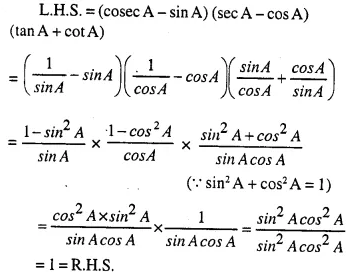
Question 18.

……

Answer 18

Question 19.

……….

Answer 19

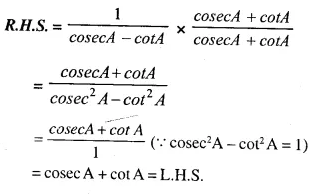
Question 20.

………..

Answer 20

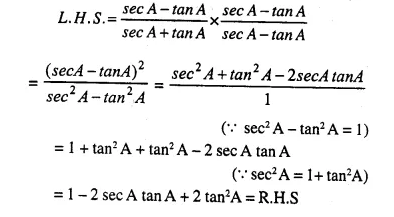
Question 21.

…………..
(sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A

Answer 21

L.H.S. = (sin A + cosecA)² + (cosA+ secA)²
= sin² A + cosec² A + 2 sin A cosec A + cos² A + sec² A + 2 cos A sec A
and = sin² A+cosec² A+2 sin A x  + cos² A+sec²A + 2cosA x 
= sin²A + cos² A + cosec² A + sec²A+ 2 + 2   (∵ sin² A + cos²A= 1)
so = 1 +cosec²A + sec²A + 4
= (1 + cot² A) + (1 + tan² A) + 5 [∵ cosec²A = 1 + cot² A and sec² A = 1 + tan²A]
hence = 1 + cot² A + 1 + tan² A + 5
= 7 + tan²A + cot²A = R.H.S.

Question 22.

sec²A. cosec²A = tan²A + cot²A + 2

Answer 22

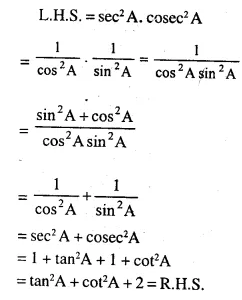
Question 23.

……..

Answer 23

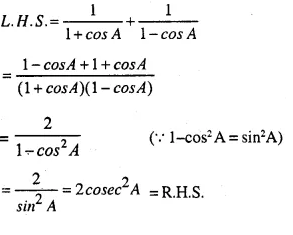
Question 24.

………..

Answer 24

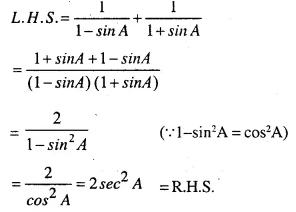
Question 25.

…………

Answer 25

Question 26.

………….

Answer 26

Question 27.

………….

Answer 27

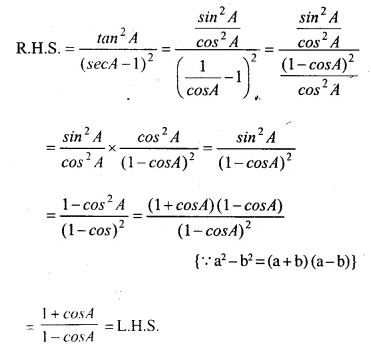
Question 28.

…………

Answer 28

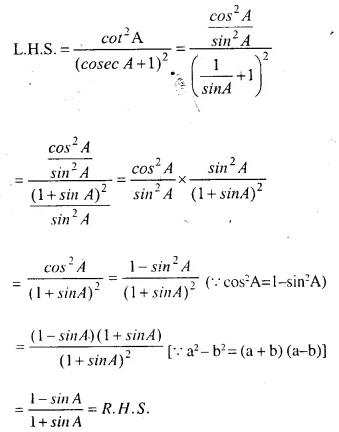
Question 29.

…………..

Answer 29

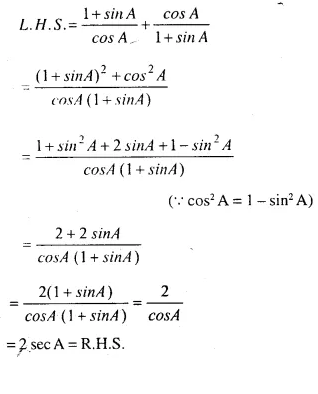
Question 30.

…………..

Answer 30

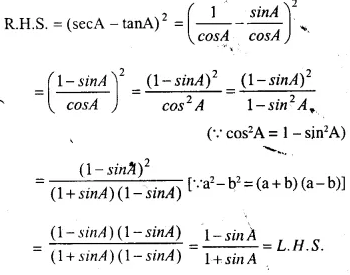
Question 31.

……………

Answer 31

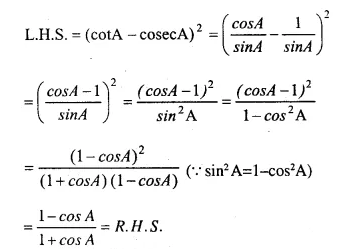
Question 32.

………….

Answer 32

Question 33.

……………

Answer 33

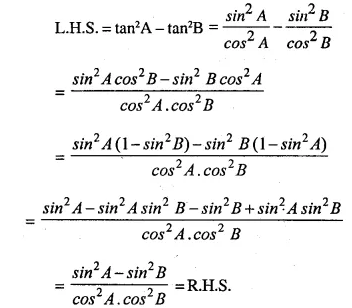
Question 34.

……………

Answer 34

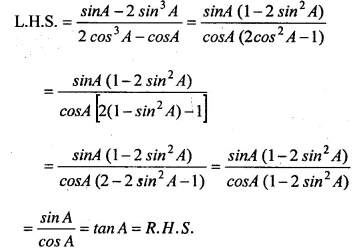
Question 35.

………………

Answer 35

Question 36.

…………..

Answer 36

Question 37.

………….

Answer 37

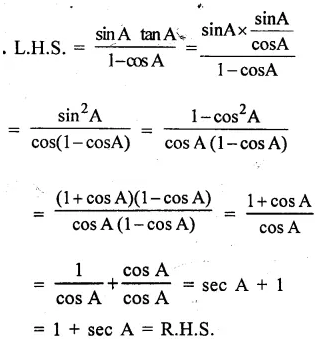
Question 38.

(1 +cot A-cosec A) (1 + tan A + sec A) = 2

Answer 38

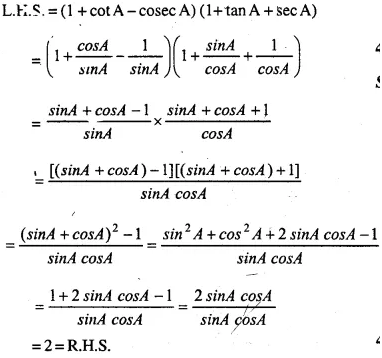
Question 39.

………..

Answer 39

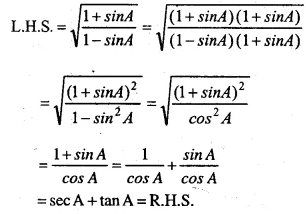
Question 40.

……………

Answer 40

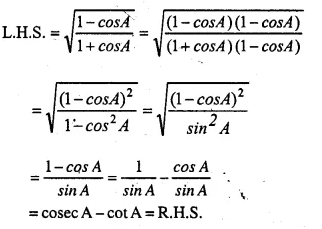
Question 41.

…………..

Answer 41

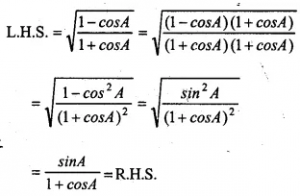
Question 42.

………….

Answer 42

Question 43.

………….

Answer 43

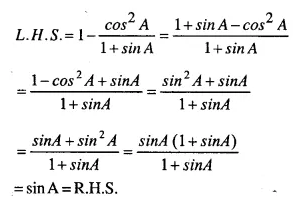
Question 44.

…………

Answer 44

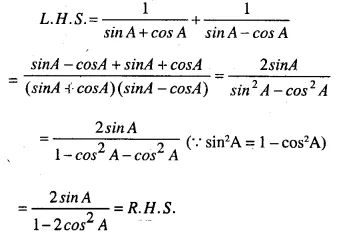
Question 45.

…………

Answer 45

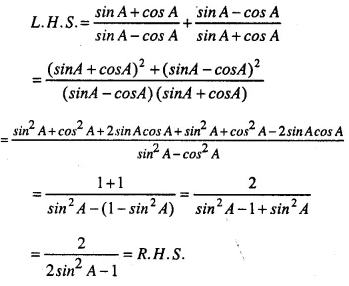
Question 46.

…………..

Answer 46

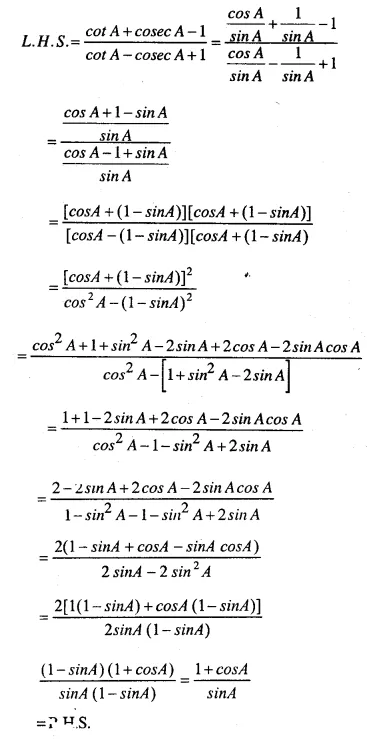
Question 47.

……………

Answer 47

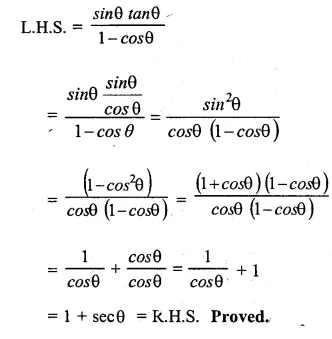
Question 48.

…………..

Answer 48

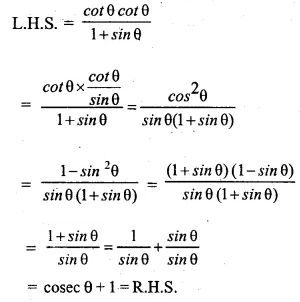
 EXERCISE – 21 (B) Solutions of Selina Concise Mathematics Chapter-20 Trigonometrical Identities 

Question 1.

Prove that: 

(i)…

(ii)…….

(iii)………

(iv)………

(v)………

(vi)……..

(vii)…….

(viii)…….

(ix)……….

Answer 1

(i)

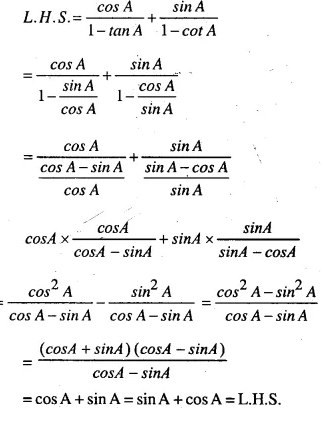
(ii)

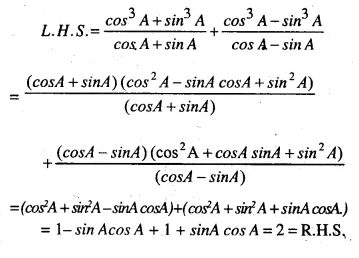
(iii)

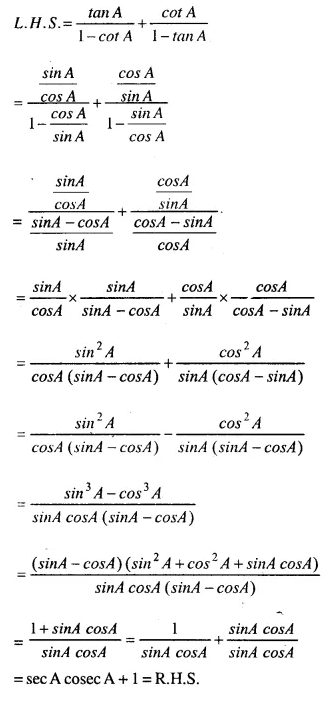
(iv)

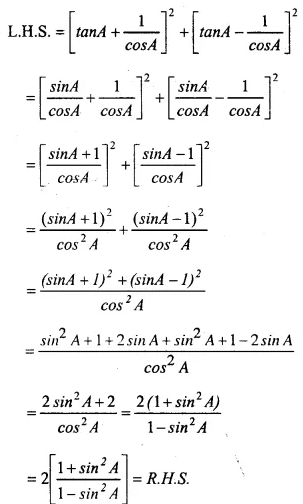
(v)

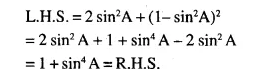
(vi)

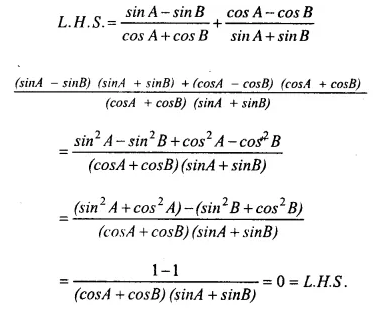
(vii)

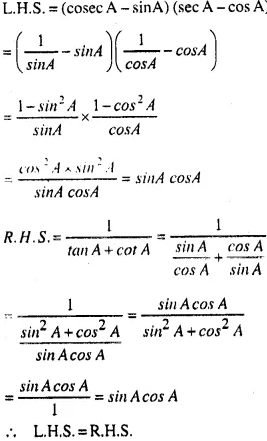
(viii)

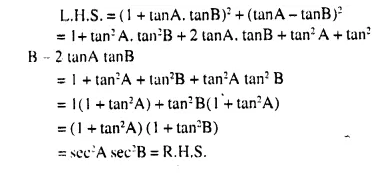
(ix)

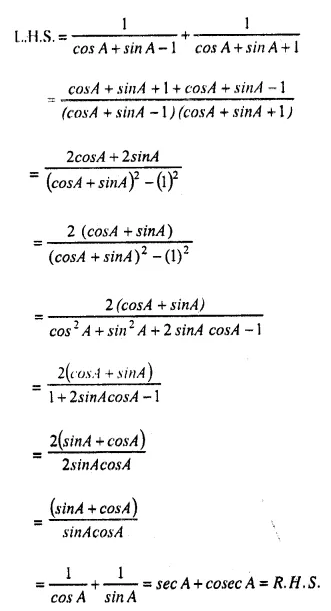
Question 2.

If xcosA + ysinA = m and xsinA-ycosA = n, then prove that: x²+y² = m² + n²

Answer 2

x cos A + y sin A = m    …(i)
x sin A – y cos A = n     ….(ii)
squaring (i) and (ii)
x² cos² A + y² sin² A + 2 xy cosA sinA = m²
x² sin² A + y² cos² A – 2 xy cos A sin A = n²
Adding we get,
x² (sin² A + cos² A) + y² (sin² A + cos² A) = m²+n²
∴ x²+y² = m² + n²(∵ sin²A + cos²A= 1)
Hence proved.

Question 3.

If m = a sec A +b tan A and n=atanA + bsecA, then prove that: m²-n² = a²-b²

Answer 3

m = asec A + btan A         ……(i)
n = a tan A + b sec A       …..(ii)
squaring (i) and (ii)
m² = a² sec² A + b² tan² A + 2ab sec A tan A
n² = a² tan² A + b² sec² A + 2 ab tan A sec A
Subtracting, we get
m² – n² = a² (sec² A – tan² A) + b² (tan² A – sec² A)
= a²x 1 +b²(-1) = a²-b² ( ∵ sec²A-tan²A= 1)  .
Henceproved

Question 4.

If x = r sin A cos B, y = r sin A sin B and z = r cos A, then prove that: x² + y² + z² = r.

Answer 4

x = r sin A cos B      ….(i)
y = r sin A sin B      ….(ii)
z = r cosA               …….(iii)
Squaring, (i), (ii) & (iii)
x²=r² sin² A cos² B,
y² = r²sin²Asin²B,
z² = r²cos²A
Adding, we get,
x²+y² + z²=r² (sin²A cos²E + sin² A sin² B+cos²A)
= r[sin²A (cos² B + sin²B) + cos²A]
and = r [sin² A x 1 + cos² A]
so = r² [sin² A + cos² A] = r² x 1  = r²        ( ∵ sin² A + cos² A = 1)
Hence proved.

Question 5.

If sin A + cos A = m and sec A + cosec A=n, show that n (m²-1) = 2m

Answer 5

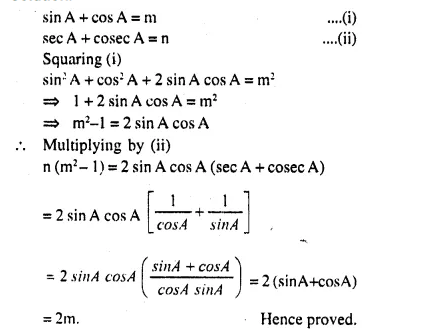
Question 6.

If x = r cos A cos B, y = r cos A sin B and z = r sin A, show that x² + y² + z² = r²

Answer 6

x = r cosAcosB              ….(i)
y = r cosAsinB             ….(ii)
z = r sinA                 ….(iii)
Squaring (i), (ii), (iii)
x² = r² cos² A cos² B, y² = r² cos² A sin²B
z² = r²sin²A
Adding, we get
x² + y² + z² = r² (cos² A cos²B + cos² A sin² B + sin² A)
= r² [cos² A (cos² B + sin²B) + sin² A]
= r²[cos²Ax 1+sin²A]
= r² (1) = r^{2    `}Hence proved.

Question 7.

…………
Answer 7

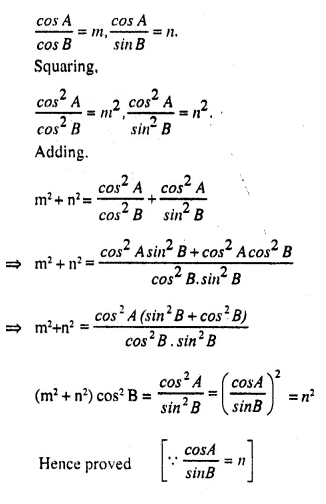
Chapter-21 Trigonometrical Identities Concise Solutions EXERCISE – 21 (C)

Question 1.

Show that:
(i) tan 10° tan 15° tan 75° tan 80° = 1
(ii) sin 42° sec 48°+cos 42° cosec 48°= 2
(iii) ………

Answer 1

(i)

tan 10° tan 15° tan 75° tan 80°= 1
L.H.S. = tan 10° tan 15° tan 75° tan 80°
= tan (90° – 80°) tan (90° – 75°) tan 75° tan 80°
and = cot 80° cot 75° tan 75° tan 80°
so = tan 80° cot 80° x tan 75° cot 75°
hence = 1 x 1 = 1= R.H.S. (∵ tan A cot A = 1)
(ii)

sin 42° sec 48°+ cos 42° cosec 48°= 2
L.H.S. = sin 42° sec 48°+ cos 42° cosec 48°
= sin 42° sec (90° – 42°) + cos 42° cosec (90° – 42°)
= sin 42° cosec 42°+ cos 42° sec 42°
=1 + 1=2 R.H.S. (∵ sin A cosec A=1, cos A sec A=1)

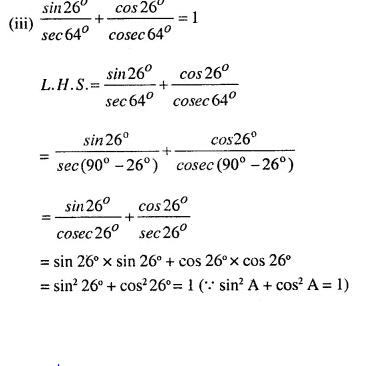
Question 2.

Express each of the following in terms of angles between 0°and 45°.
(i) sin 59° + tan 63°
(ii) cosec 68° + cot 72°
(iii) cos 74° + sec 67°

Answer 2

(i)

sin 59° + tan 63°
= sin (90° – 31°) + tan (90° – 27°)
= cos 31°+ cot 27°
(ii)

cosec 68° + cot 72°
= cosec (90° – 22°) + cot (90° – 18°)
= sec 22°+ tan 18°
(iii)

cos 74°+ sec 67°
= cos (90° – 16°) + sec (90° – 23°)
= sin 16°+ cosec 23°

Question 3.

Show that:
…………

Answer 3

Question 4.

For triangle ABC, Show that:

Answer 4

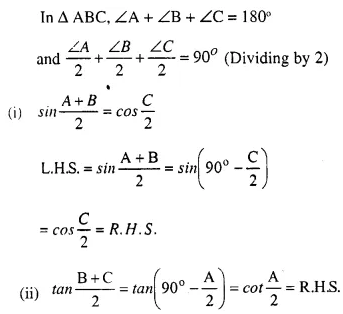
Question 5.

Evaluate:

(i)…

(ii)…….

(iii)………

(iv)………

(v)………

(vi)……..

(vii)…….

(viii)…….

(ix)……….

Answer 5

(i)

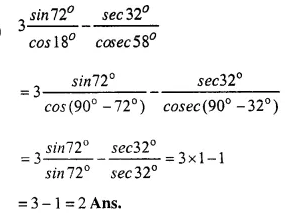
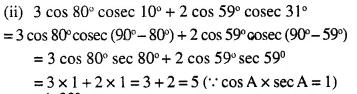
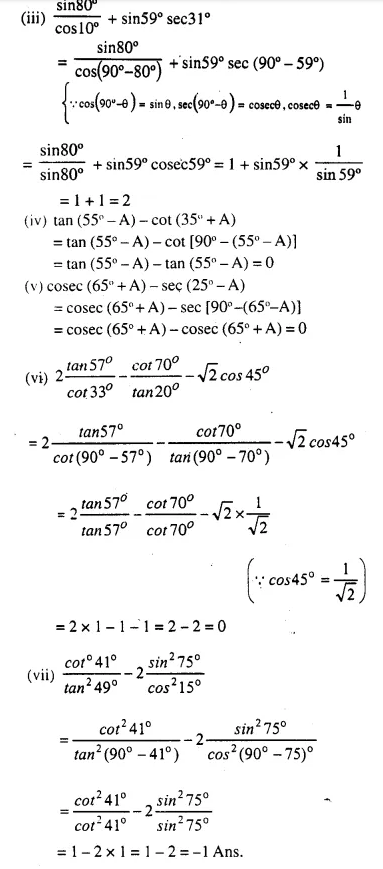
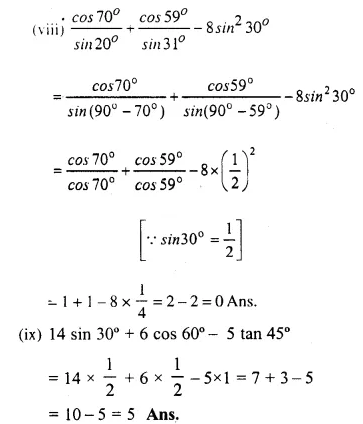
Question 6.

………..

Answer 6

Question 7.

Find (in each case, given below) the value of x, if:
(i) sin x = sin 60° cos 30° – cos 60° sin 30°
(ii) sin x = sin 60° cos 30° + cos 60° sin 30°
(iii) cos x = cos 60° cos 30° – sin 60° sin 30°
(iv) ………….
(v) sin 2x = 2 sin 45° cos 45° 
(vi) sin 3x = 2 sin 30° cos 30°
(vii) cos (2x – 6°) = cos² 30° – cos² 60°

Answer 7

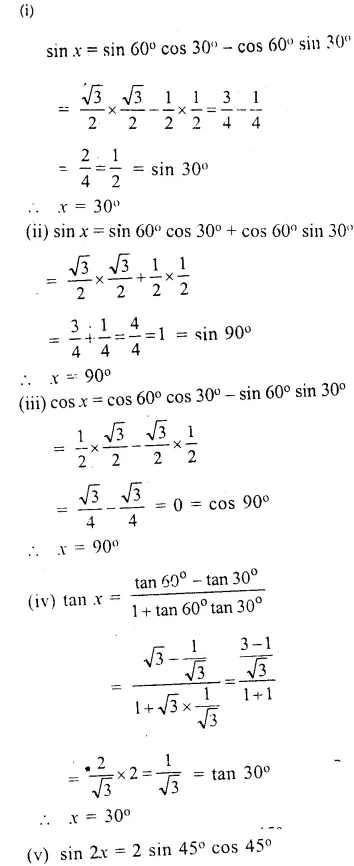
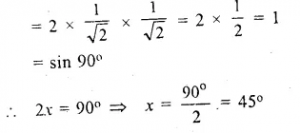
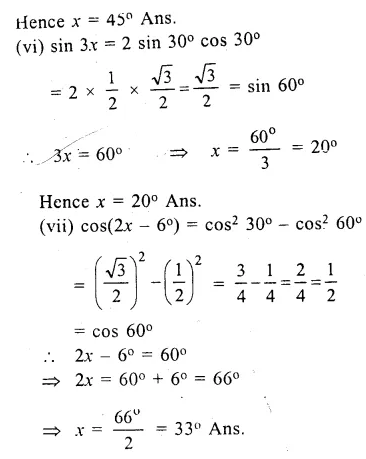
Question 8.

In each case, given below, find the value of angle A, where 0° ≤ A ≤ 90°.
(i) sin (90° – 3A). cosec 42° = 1
(ii) cos (90° – A). sec 77° = 1

Answer 8

Question 9.

Prove that:

…………….

Answer 9

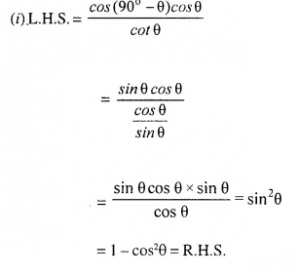
Question 10.

Evaluate:

………….

Answer 10

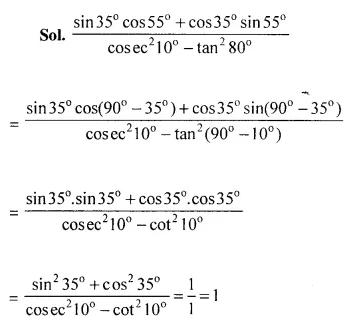
Question 11.

Without using trigonometric tables, evaluate sin² 34° + sin² 56° + 2 tan 18° tan 72° – cot² 30°.

Answer 11

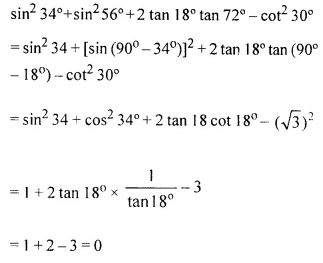
Question 12.

Without using trigonometrical tables, evaluate: cosec² 57° – tan² 33° + cos 44° cosec 46° –  cos45°- tan² 60°

Answer 12

Selina Publishers Concise Maths Solutions of EXERCISE – 21 (D)Trigonometrical Identities 

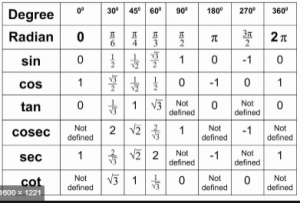
Question 1.

Use tables to find sine of:
(i) 21°
(ii) 34°42′
(iii) 47° 32′                    
(iv) 62°57′
(v) 10°20′ + 20° 45′

Answer 1

From tables of sine of angles, we find that:
(i)

sin 21°= 0.3584,
(ii)

sin 34°42’= .5693
(iii)

sin 47° 32′ = 0.7377
(iv)

sin 62° 57′ = 0.8906
(v)

sin 10° 20′ + 20°45′ = sin 31°5′
= 0.5162

Question 2.

Use tables to find cosine of:
(i) 2°4′
(ii) 8°12′
(iii) 26°32’                     
(iv) 65°41′
(v) 9°23′ +15°54′

Answer 2

From tables of cosine of angle, we find that:
(i)

cos 2°4′ = 0.9993
(ii)

cos 8° 12’ = 0.9898
(iii)

cos 26°32′ = 0.8946
(iv)

cos 65°41′ = 0.4118
(v)

 cos 9°23′ + 15°54′ = cos 25° 17′
= 0.9042

Question 3.

Use trigonometrical tables to find tangent of:
(i) 37°
(ii) 42°18′
(iii) 17°27′

Answer 3

From the tables of tangents, we find that
(i)

tan 35° = 0.7536
(ii)

tan 42°18’= 0.9099
(iii)

tan 17°27’= 0.3144

Question 4.

Use tables to find the acute angle θ, if the value of sin θ
(i) 4848
(ii) 0.3827
(iii) 0.6525

Answer 4

From the tables of series, we find that of :
(i)

sinθ = 0.4848, then θ = 29°
(ii)

sinθ = 0.3827, then θ = 20° 30′
(iii)

sin θ = 0.6525, then θ = 40° 42’ + 2′ = 40°44′

Question 5.

Use tables to find the acute angle θ, if the value of cos θ is :
(i) 0.9848
(ii) 0.9574
(iii) 0.6885

Answer 5

From the tables of cosines, we find that if :
(i)

cos θ = 0.9848, then θ = 10°
(ii)

cos θ = 0.9574, then θ = 16°48′- 1’=16°47’
(iii)

cos θ = 0.6885, then θ = 46° 30′ or 46°30′
= 46° 29’

Question 6.

Use tables to find the acute angle θ, if the value of tan θ is :
(i) 2419
(ii) 0.4741
(iii) 0.7391                     
(iv) 1.06

Answer 6

From the table of tangents, we find that if:
(i)

tan θ = 0.2419, then θ=13° 36’
(ii)

tan θ = 0.4741, then θ = 25° 18’ + 4’ = 25°22′
(iii)

tan θ = 0.7391, then θ= 36°24’+ 4′ = 36°28′
(iv)

tan θ = 1.06, then θ = 46°36′ + 4′ = 46°40′

Question 7.

If sin θ=0.857; find:
(i) θ                              
(ii) tan θ

Answer 7

From the tables of T. Ratio’s we find this :
(i)

If sin θ = 0.857, then θ = 58°54′ + 4.5′ = 58° 58′ or 58°59’
(ii)

tan 58°58’= 1.6577 +43 = 1.662 or tan 58° 59′ = 1.6577 + 53 = 1.663

Question 8.

If θ is the acute angle and cos θ = 0.7258; find:
(i) θ
(ii) 2 tan θ – sin θ

Answer 8

From the tables of T-ratio’s, we find that:
(i)

If cos θ = 0.7258, then θ= 43° 30′ -2′ = 43°28’
(ii)

Now 2 tan θ – sin θ= 2 tan 43°28′ – sin 43°28′
2 tan 43°28’ = 2 x (0.9457 + 0.0022)
= 0:9479 x 2 = 1.8958
and sin 43°28′ = 0.6871 + 0.0008 = 0.6879
∴ 2 tan 43°28′ – sin 43° 28′ = 1.8958 – 0.6879 = 1.2079

Question 9.

Let θ be an acute angle and tan θ = 0.9490 find:
(i) θ
(ii) cos θ
(iii) sin θ – cos θ

Answer 9

From the tables of T-raios, we find that:
(i)

if tan θ = 0.9490 , then θ = 43°30′
(ii)

cos θ = cos 43°30′ = 0.7254
(iii)

sin θ = sin 43°50′ = 0.6884
∴ sin θ – cos θ = 0.6884 – 0.7254 = -0.0370 = -0.037

 Concise Selina Maths Solutions EXERCISE  – 21 (E)Trigonometrical Identities 

 

Question 1.

Prove the following identities :

(i)…

(ii)…….

(iii)………

(iv)………

(v)………

(vi)……..

(vii)…….

(viii)…….

(ix)………

 (x)……….

(xi)……….

(xii)……….

(xiii)……….

(xiv)……….

(xv)……….

(xvi)……….

(xvii)……….

Answer :1

Answer (i)

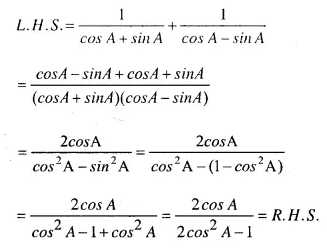
Answer :(ii)

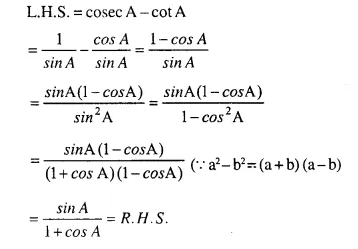
Answer :(iii)

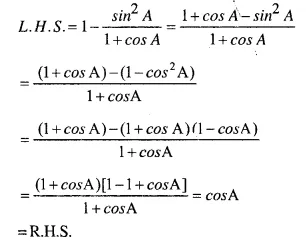
Answer :(iv)

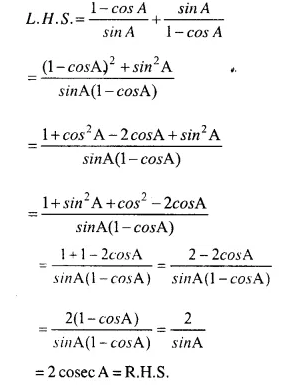
Answer :(v)

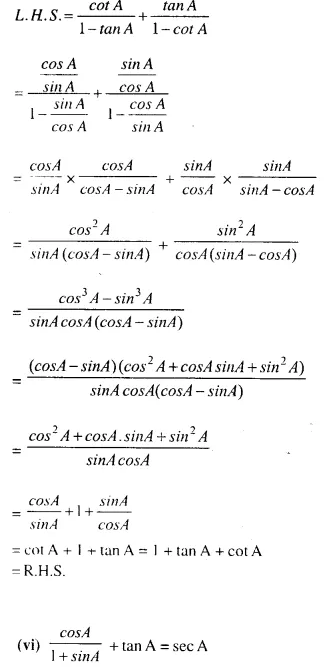
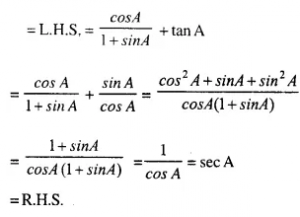
Answer :(vii)

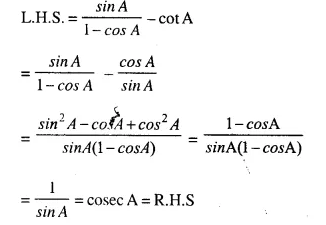
Answer :(viii)

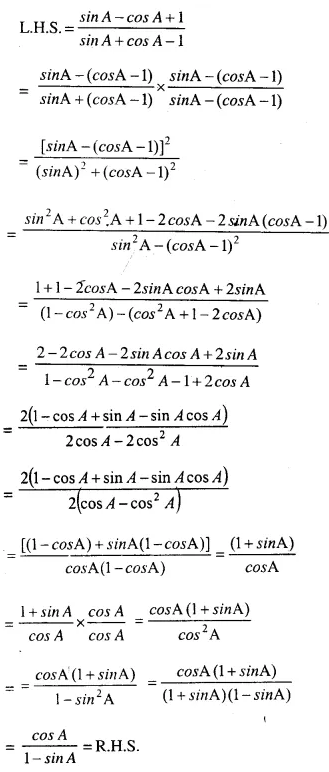
Answer :(ix)

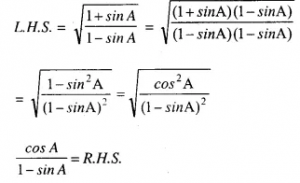
Answer :(x)

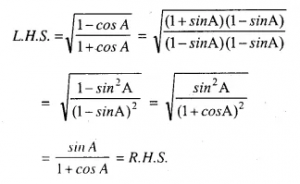
Answer :(xi)

Answer :(xii)

Answer :(xiii)

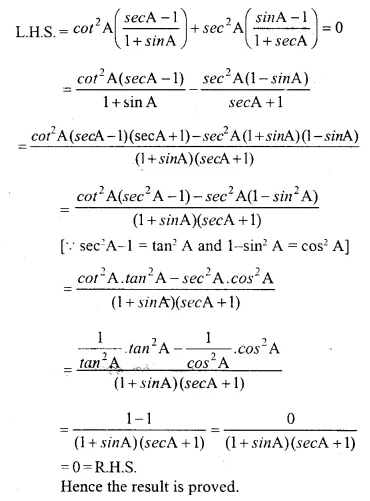
Answer :(xiv)

Answer :(xv)

Answer :(xvi)

Answer (xvii)

Question 2.

If sin A + cos A = p and sec A + cosec A = q then prove that: q(p² – 1) 2p

Answer 2

Question 3.

………….

Answer 3

Question 4.

…………

Answer 4

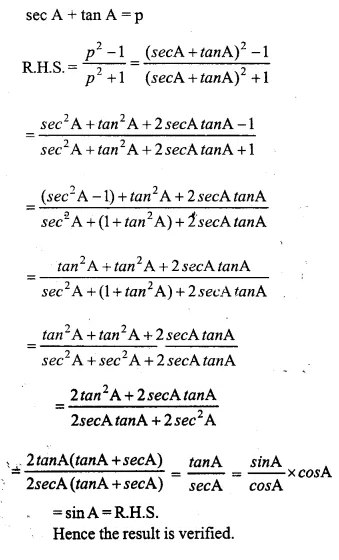
Question 5.

If tan A=n tan B and sin A=m sin B, prove that:

………

Answer 5

Question 6.

(i) If 2 sin A-1 = 0, show that:
sin 3 A = 3 sin A – 4 sin³ A.             [2001]
(ii) If 4cos² A-3 = 0, show that:
cos 3A = 4 cos³ A – 3 cos A

Answer 6

Question 7.

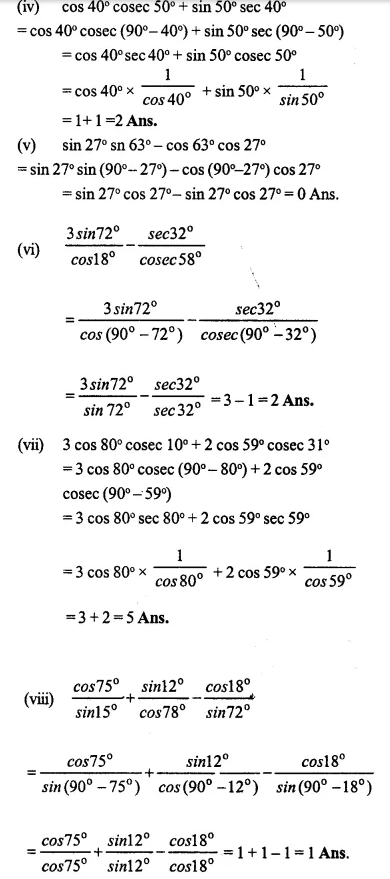
Evaluate:

(i)……

(ii)…….

(iii)………

(iv)………

(v)………

(vi)……..

(vii)…..

Answer 7

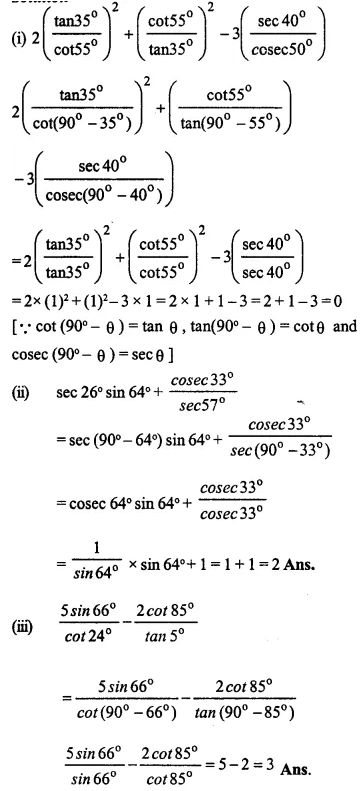
Question 8.

Prove that:

(i)……

(ii)…….

(iii)………

(iv)………

(v)………

Answer 8

Question 9.

If A and B are complementary angles, prove that:
(i) cot B + cos B sec A cos B (1 + sin B)
(ii) cot A cot B – sin A cos B – cos sin B = 0
(iii) cosec² A + cosec² B = cosec² A cosec² B

 (iv) ………..

Answer 9

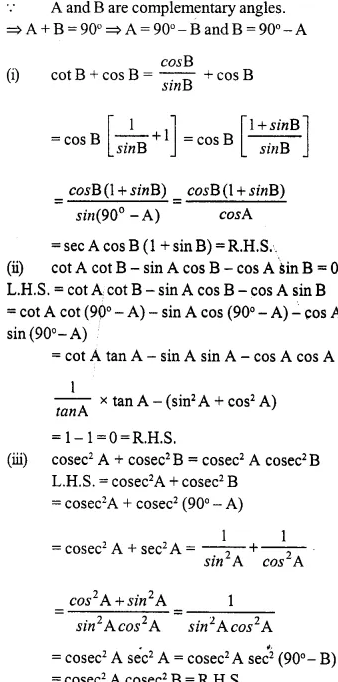
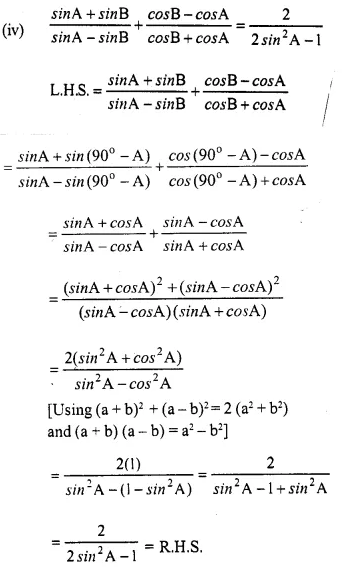
Question 10.

Prove that:

(i)…

(ii)…….

(iii)………

(iv)………

(v)………

(vi)……..

(vii)…….

(viii)…….

(ix)………

 (x)……….

Answer 10

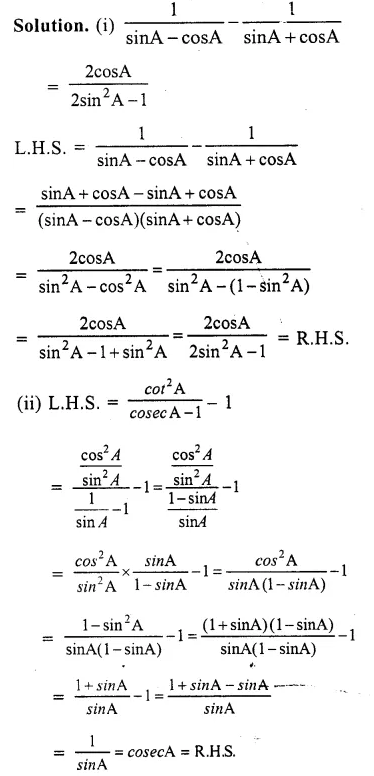
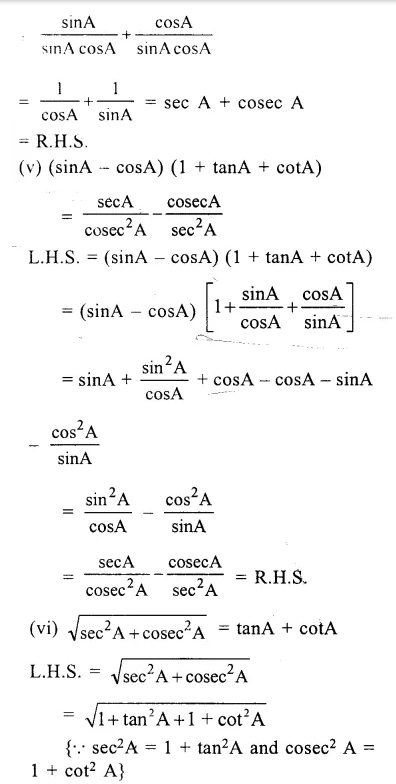
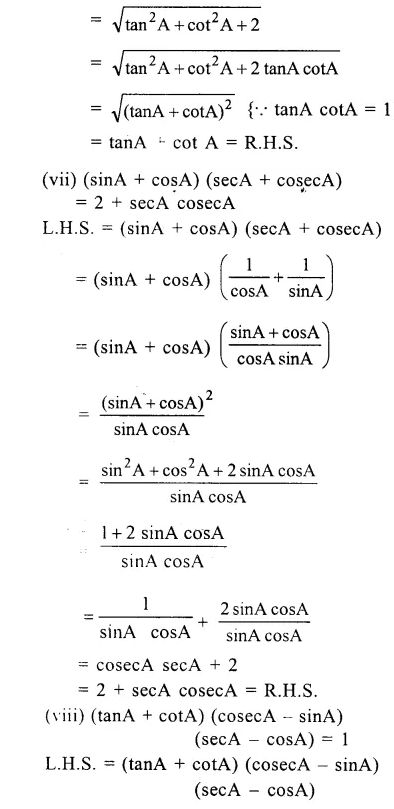
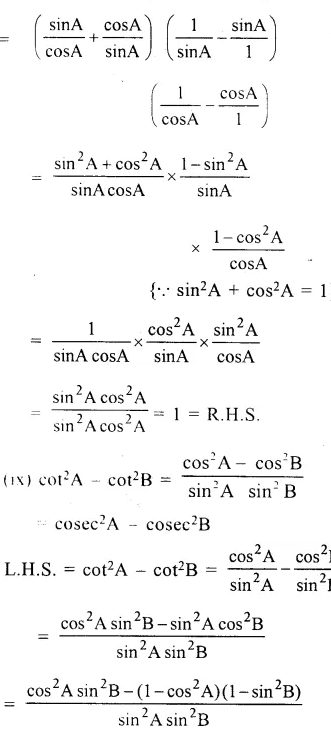
(x)

Question 11.

If 4 cos² A – 3 = 0 and 0° ≤ A ≤ 90°, then prove that : 
(i) sin 3A = 3 sinA – 4 sin³A
(ii) cos 3A = 4 cos³ A – 3 cos A

Answer 11

 

Question 12.

Find A, if 0° ≤ A ≤ 90° and :
(i) 2 cos² A – 1 = 0
(ii) sin 3A – 1 = 0
(iii) 4 sin² A – 3 = 0
(iv) cos² A – cos A = 0
(v) 2cos² A + cos A – 1 = 0

Answer 12

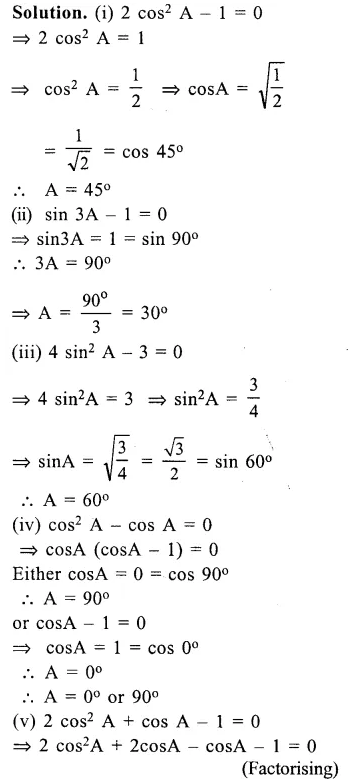
Question 13.

If 0° < A < 90° ; find A, if :

………

Answer 13

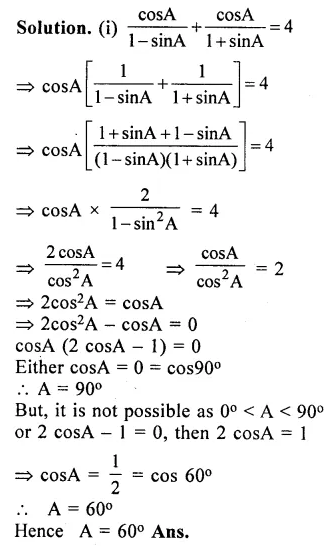
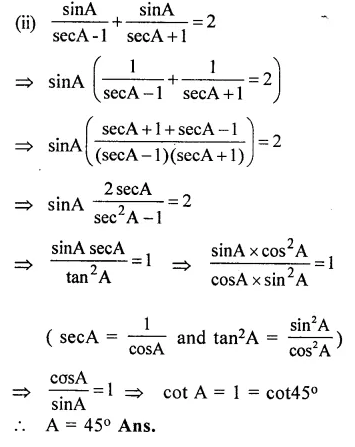
Question 14.

Prove that : (cosec A – sin A) (sec A – cos A) sec² A = tan A. (2011)

Answer 14

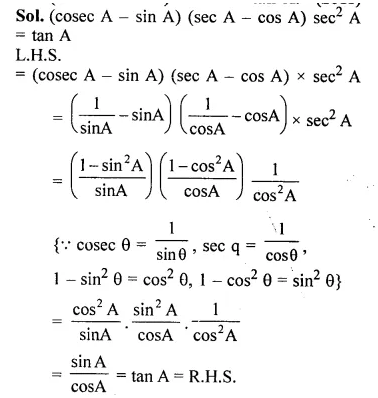
Question 15.

Prove the identity : (sin θ + cos θ) (tan θ + cot θ) = sec θ + cosec θ. (2014)

Answer 15

Question 16

Evaluate without using trigonometric tables,

sin² 28° + sin² 62° + tan² 38° – cot² 52° + sec² 30°

Answer 16

sin² 28° + sin² 62° + tan² 38° – cot² 52° + sec² 30° 

= sin² 28° + [sin (90 – 28)°]² + tan² 38° – [cot(90 – 38)°]² + sec² 30°

= sin² 28°  + cos² 28° + tan² 38° – tan² 38° + sec² 30°

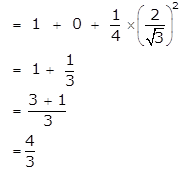
 End of Trigonometrical Identities Concise Solutions Chapter-21

Return to :- Concise Selina  Maths Solutions for ICSE Class-10

Thanks

Please share with your friends