ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths Solutions Ch-17. Step by Step Solutions of Exe-17 questions on Trigonometrical Ratios of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-17 | Trigonometrical Ratios |
| Topics | Solution of Exe-17 Questions |
| Academic Session | 2024-2025 |
Exe-17 Solutions of ML Aggarwal for ICSE Class-9 Ch-17, Trigonometrical Ratios
Question 1. (a) From the figure (1) given below, find the values of:
(i) sin θ
(ii) cos θ
(iii) tan θ
(iv) cot θ
(v) sec θ
(vi) cosec θ
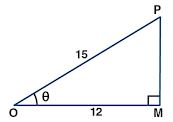
(b) From the figure (2) given below, find the values of:
(i) sin
(ii) cos A
(iii) sin2 A + cos2 A
(iv) sec2 A – tan2 A.
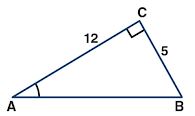
Answer :
(a) From right angled triangle OMP,
By Pythagoras theorem,
OP2 = OM2 +MP2
⇒ MP2 = OP2 + OM2
⇒ MP2 = (15)2 – (12)2
⇒ MP2 = 225 – 144
⇒ MP2 = 81
⇒ MP2 = 92
⇒ MP = 9
(i) sin θ = MP/OP
= 9/15
= 3/5
(ii) cos θ = OM/OP
= 12/15
= 4/5
(iii) tan θ = MP/OP
= 9/12
= ¾
(iv) cot θ = OM/MP
= 12/9
= 4/3
(v) sec θ = OP/OM
= 15/12
= 5/4
(vi) cosec θ = OP/MP
= 15/9
= /3
(b) From right angled triangle ABC,
By Pythagoras theorem,
AB2 = AC2 + BC2
⇒ AB2 = (12)2 + (5)2
⇒ AB2 = 144 + 25
⇒ AB2 = 169
⇒ AB2 = 132
⇒ AB = 13
(i) sin A = BC/AB
= 5/13
(ii) cos A = AC/AB
= 12/13
(iii) sin2 A + cos2 A = (BC/AB)2 + (AC/AB)2
= (5/13)2 + (12/13)2
= (25/169) + (144/169)
= (25 + 144)/ 169
= 169/169
= 1
sin2 A + cos2 A = 1
(iv) sec2 A – tan2 A = (AB/AC)2 – (BC/AC)2
= (13/12)2 – (5/12)2
= (169/144) – (25/144)
= (169 – 25)/144
= 144/144
= 1
sec2 A – tan2 A = 1
(ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths)
Question 2.
(a) From the figure (1) given below, find the values of:
(i) sin B (i) cos C (iii) sin B + sin C (iv) sin B cos C + sin C cos B
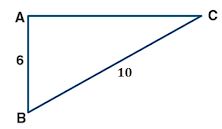
(b) From the figure (2) given below, find the values of:
(i) tan x
(ii) cos y
(iii) cosec2 y – cot2 y
(iv) 5/sin x + 3/sin y – 3 cot y.
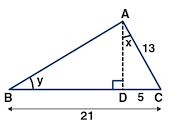
Answer :
(a) From right angled triangle ABC,
By Pythagoras theorem, we get
BC2 = AC2 + AB2
⇒ AC2 = BC2 – AB2
⇒ AC2 = (10)2 – (6)2
⇒ AC2 = 100 – 36
⇒ AC2 = 64
⇒ AC2 = 82
⇒ AC = 8
(i) sin B = perpendicular/ hypotenuse
= AC/BC
= 8/10
= 4/5
(ii) cos C = Base/hypotenuse
= AC/BC
= 8/10
= 4/5
(iii) sin B = Perpendicular/hypotenuse
= AC/BC
= 8/10
= 4/5
sin C = perpendicular/hypotenuse
= AB/BC
= 6/10
= 3/5
Now,
sin B + sin C = (4/5) + (3/5)
= (4 + 3)/5
= 7/5
(iv) sin B = 4/5
cos C = 4/5
sin C = perpendicular/ hypotenuse
= AB/BC
= 6/10
= 3/5
cos B = Base/Hypotenuse
= AB/BC
= 6/10
= 3/5
sin B cos C + sin C cos B
= (4/5)×(4/5) + (3/5)×(3/5)
= (26/25) + (9/25)
= (16+9)/25
= 25/25
= 1
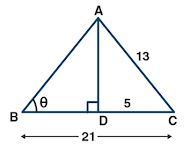
(b) From Figure
AC = 13, CD = 5, BC =21,
BD = BC – CD
= 21 – 5
= 16

From right angled ∆ACD,
AC = AD2 + CD2
⇒ AD2 = AC2 – CD2
⇒ AD2 = (13)2 – (5)2
⇒ AD2 = 169 – 25
⇒ AD2 = 144)
⇒ AD2 = (12)2
⇒ AD = 12
From right angled ∆ABD,
AB2 = AD2 + BD2
⇒ AB2 = 400
⇒ AB2 = (20)2
⇒ AB = 20
(i) tan x = perpendicular/Base (in right angled ∆ACD)
=CD/AD
= 5/12
(ii) cos y = Base/Hypotenuse (in right angled ∆ABD)
= BD/AB
= (20)/12 – (5/3)
cot y = Base/Perpendicular (in right ∆ABD)
=BD/AB
= 16/20 = 4/5
(iii) cos y = Hypotenuse/ perpendicular (in right angled ∆ABD)
BD/AB
= 20/12
= 5/3
cot y = Base/Perpendicular (in right ∆ABD)
AB/AD
= 16/12
= 4/3
cosec2 y – cot2 y = (5/3)2 – (4/3)2
= (25/9) – (16/9)
= (25-16)/9
= 9/9
= 1
Therefore,
cosec2 y – cot2 y = 1
(iv) sin x = Perpendicular/Hypotenuse (in right angled ∆ACD)
= AD/AB
= 12/20
= 3/5
cot y = Base/Perpendicular (in right angled ∆ABD)
= BD/AD
= 16/12
= 4/3
(5/sin x) + (3/sin y) – 3cot y
= [5/(5/13)] + 3/(3/5) – (3 × 4/3)
= (5× 13/5) + (3× 5/3) – (3× 4/3)
= (1× 13/1) + (1× 5/1) – (1× 4/1)
= 13 + 5 – 4
= 18 – 4
= 14
Hence,
5/sin x + 3/sin y – 3cot y = 14
Trigonometrical Ratios Exercise-17
ML Aggarwal Class 9 ICSE Maths Solutions
Page 413
Question 3.
(a) From the figure (1) given below, find the value of sec θ.
(b) From the figure (2) given below, find the values of:
(i) sin x
(ii) cot x
(iii) cot2 x- cosec2 x
(iv) sec y
(v) tan2 y – 1/cos2 y.
Answer :
(a) From the figure, Sec θ = AB/BD
But in ∆ADC, ∠D = 90o
AC2 =AD2 + DC2
⇒ (13)2 =AD2 + 25
⇒ AD2 = 169 -25
= 144
= (12)2
⇒ AD = 12
AB2 = AD2 + BD2 (in right ∆ABD)
= (12)2 + (16)2
= 144 + 256
= 400
= (20)2
⇒ AB = 20
Sec θ = AB/BD
= 20/16
= 5/4
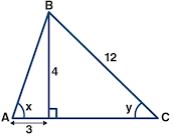
(b) let given ∆ABC
BD = 3, AC = 12, AD = 4
In right angled ∆ABD
AB2 =AD2 + BD2
⇒ AB2 = (4)2 + (3)2
⇒ AB2 = 16 + 9
⇒ AB2 = 25
⇒ AB2 = (5)2
⇒ AB = 5
In right angled triangle ACD
AC2 = AD2 + CD2
⇒ CD2 = AC2 – AD2
⇒ CD2 = (12)2 – (4)2
⇒ CD2 = 144 – 16
⇒ CD2 = 128
⇒ CD = √128
⇒ CD = √64 × 2 CD
= 8√2
(i) sin x = perpendicular/Hypotenuse
= AD/AB
= 4/5
(ii) cot x = Base/Perpendicular
= BD/AD
= ¾
(iii) cot x = Base/Perpendicular
BD/AD
= 3/4
(iv) cosec x = Hypotenuse/Perpendicular
AB/BD
= 5/4
cot2 x – cosec2 x
= (3/4)2 – (5/4)2
= 9/16 – 25/16
(9 -25)/16
= -16/16
= -1
Perpendicular = Hypotenuse/Base (in right angled ∆ACD)
= AD/CD
= 12/(8 √2)
= 3/(2 √2)
cot y = Base/Hypotenuse
= AD/CD
= 4/8 √ 2
= 1/2 √2
cot y = Base/Hypotenuse (in right angled ∆ACD)
= CD/AC
= 8√2/12
= 2√/3
Now tan2 y = 1/cos2 y
= (1/2√2)2 – 1/(2√2/3)2
= ¼ × – ¼ × 2
= (1/8) – (9/8)
= (1-9)/8
= -8/8
= -1
tan2 y – 1/cos2 y = –1
(ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths)
Question 4.
(a) From the figure (1) given below, find the values of:
(i) 2 sin y- cos y
(ii)2sinx-cosx
(iii) 1- sin x + cos y
(iv) 2 cos x-3 sin y +4 tan z.
(b) In the figure (2) given below, ∆ABC is right-angled at B. If AB = y units, BC = 3 units and CA = 5 units, find
(i) sin x°
(ii) y.
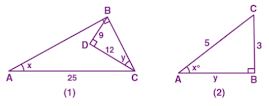
Answer :
(a) In a right angled ∆BCD,
BC2 = BD2 + CD2
BC2 = 92 + 122
BC2 = 81 + 144 = 225
⇒ BC2 = 152
⇒ BC = 15
In a right angled ∆ABC,
AC2 = AB2 + BC2
AB2 = AC2 – BC2
AB2 = 252 – 152
AB2 = 625 – 225 = 400
So we get
AB2 = 202
AB = 20
(i)
In right angled ∆BCD
sin y = perpendicular/ hypotenuse
⇒ sin y = BD/ BC
sin y = 9/15 = 3/5
In right angled ∆BCD
cos y = base/hypotenuse
⇒ cos y = CD/BC
cos y = 12/15 = 4/5
2sin y – cos y = 2× 3/5 – 4/5
= 6/5 – 4/5
= 2/5
Therefore, 2 sin y – cos y = 2/5
(ii) In right angled ∆ABC
sin x = perpendicular/ hypotenuse
sin x = BC/AC
sin x = 15/25 = 3/5
In right angled ∆ABC
cos x = base/hypotenuse
⇒ cos x = AB/AC
cos x = 20/25 = 4/5
2 sin x – cos x = 2× 3/5 – 4/5
= 6/5 – 4/5
= 2/5
Therefore, 2 sin x – cos x = 2/5.
(iii) In right angled ∆ABC
sin x = perpendicular/hypotenuse
⇒ sin x = BC/AC
sin x = 12/25 = 3/5
In right angled ∆BCD
cos y = base/hypotenuse
⇒ cos y = CD/BC
cos y = 12/15 = 4/5
1 – sin x + cos y
= 1 – 3/5 + 4/5
= (5 – 3 + 4)/ 5
So we get
= (9 – 3)/ 5
= 6/5
Therefore, 1 – sin x + cos y = 6/5.
(iv) In right angled ∆BCD
cos x = base/hypotenuse
⇒ cos x = AB/AC
cos x = 20/25 = 4/5
In right angled ∆BCD
sin y = perpendicular/hypotenuse
⇒ sin y = BD/BC
sin y = 9/15 = 3/5
In right angled ∆ABC
tan x = perpendicular/base
⇒ tan x = BC/AB
tan x = 15/20 = ¾
Here,
2 cos x – 3 sin y + 4 tan x = (2× 4/5) – (3× 3/5) + (4× ¾)
= 8/5 – 9/5 3/1
Taking LCM
= (8 – 9 + 15)/5
= (23 – 9)/ 5
= 14/5
(b) AB = y units, BC = 3 units, CA = 5 units
(i) In right angled ∆ABC
sin x = perpendicular/hypotenuse
⇒ sin x = BC/AC
sin x = 3/5
(ii) In right angled ∆ABC
AC2 = BC2 + AB2
We can write it as
AB2 = AC2 – BC2
AB2 = 52 – 32
AB2 = 25 – 9 = 16
So we get
AB2 = 42
⇒ AB = 4
y = 4 units
Hence,
y = 4 units.
Question 5. In a right-angled triangle, it is given that angle A is an acute angle and that Tan A=5/12 Find the values of:
(i) cos A
(ii) cosec A- cot A.
Answer :
ABC is right angled triangle
∠A is an acute angle and ∠C = 90o
tan A = 5/12
⇒ BC/AC =5/12
Let BC = 5x and AC = 12x
From right angled ∆ABC
AB2 = (5x)2 + (12x)2
⇒ AB2 = 25x2 + 144x2
⇒ AB2 = 169x2
(i) cos A = Base/ Hypotenuse
= AC / AB
= 12x/13x
=12/13
(ii) cosec A = Hypotenuse/perpendicular
= AC / BC
= 13x /5x
= 13/5
cosec A – cot A = 13/5 – 12/5
= (13-12)/5
= 1/5
Question 6
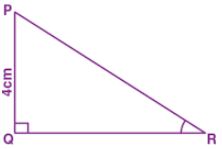
(a) In ..ABC, A = 90°. If AB 7 cm and BC- AC 1 cm, find :
(1) sin C
(i) tan B
(b) In …PQR,Q = 90°. If PQ = 40 cm and PR + QR = 50 cm, find :
(1) sin P
(ii) cos P
(ti) tan R
Answer :
(a) In right ∆ABC
∠A = 90°
AB = 7 cm
BC – AC = 1 cm
⇒ BC = 1 + AC
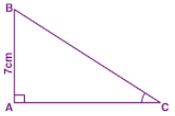
BC2 = AB2 + AC2
Substituting the value of BC
(1 + AC)2 = AB2 + AC2
⇒ 1 + AC2 + 2AC = 72 + AC2
1 + AC2 + 2AC = 49 AC2
⇒ 2AC = 49 – 1 – 48
AC = 48/2 = 24 cm
Here,
BC = 1 + AC
BC = 1 + 24 = 25 cm
(i) sin C = AB/BC = 7/25
(ii) tan B = AC/AB = 24/7
(b) In right ∆PQR
∠Q = 90°
PQ = 40 cm
⇒ PQ + QR = 50 cm
We can write it as
PQ = 50 – QR
PR2 = PQ2 + QR2
⇒ (50 – QR)2 = (40)2 + QR2
2500 + QR2 – 100QR = 1600 + QR2
So we get
2500 – 1600 = 100QR
⇒ 100QR = 900
QR = 900/100 = 9
We get
PR = 50 – 9 = 41
(i) sin P = QR/PR = 9/41
(ii) cos P = PQ/PR = 40/41
(iii) tan R = PQ/QR = 40/9
Trigonometrical Ratios Exercise-17
ML Aggarwal Class 9 ICSE Maths Solutions
Page 414
Question 7.
In triangle ABC, AB = 15 cm, AC = 15 cm and BC = 18 cm. Find
(i) cos ∠ABC
(ii) sin ∠ACB.
Answer :
Here,
ABC is a triangle in which
AB = 15 cm, AC = 15 cm and BC = 18 cm
Draw AD perpendicular to BC , D is mid-point of BC.
Then, BD – DC = 9 cm
in right angled triangle ABD,
AB2 = AD2 + BD2
⇒ AD2 = AB2 – BD2
⇒ AD2 = (15)2 – (9)2
⇒ AD2 = 225 – 81
⇒ AD2 = 144
⇒ AD – 12 cm
(i) cos ∠ABC = Base/Hypotenuse
(In right angled ∆ABD, ∠ABC = ∠ABD)
= BD / AB
= 9/15
= 3/5
(ii) sin ∠ACB = sin ∠ACD
= perpendicular/ Hypotenuse
= AD/AC
= 12/15
= 4/5
(ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths)
Question 8.
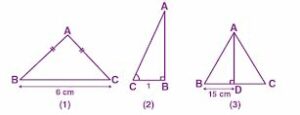
(a) In the figure (1) given below, ∆ABC is isosceles with AB = AC = 5 cm and BC = 6 cm. Find
(i) sin C
(ii) tan B
(iii) tan C – cot B.
(b) In the figure (2) given below, ∆ABC is right-angled at B. Given that ∠ACB = θ, side AB = 2 units and side BC = 1 unit, find the value of sin2 θ + tan2 θ.
(c) In the figure (3) given below, AD is perpendicular to BC, BD = 15 cm, sin B = 4/5 and tan C = 1.
(i) Calculate the lengths of AD, AB, DC and AC.
(ii) Show that tan2 B – 1/cos2 B = – 1.
Answer :
(a) ∆ABC is isosceles with AB = AC = 5 cm and BC = 6 cm
Construct AD perpendicular to BC
D is the mid point of BC
So BD = CD
BD = CD = 6/2 = 3 cm
In right angled ∆ABD
AB2 = AD2 + BD2
AD2 = AB2 – BD2
AD2 = 52 – 32
AD2 = 25 – 9 = 16
AD2 = 42
AD = 4 cm
(i) In right angled ∆ACD
sin C = perpendicular/hypotenuse
sin C = AD/AC = 4/5
(ii) In right angled ∆ABD
tan B = perpendicular/base
tan B = AD/BD = 4/3
(iii) In right angled ∆ACD
tan C = perpendicular/base
⇒ tan C = AD/CD = 4/3
In right angled ∆ABD
cot B = base/perpendicular
⇒ cot B = BD/AD = ¾
tan C – cot B = 4/3 – ¾
Taking LCM,
tan C – cot B = (16 – 9)/12 = 7/12
(b) It is given that
∆ABC is right-angled at B
AB = 2 units and BC = 1 unit
In right angled ∆ABC
AC2 = AB2 + BC2
AC2 = 22 + 12
⇒ AC2 = 4 + 1 = 5
AC2 = 5
⇒ AC = √5 units
In right angled ∆ABC
sin θ = perpendicular/hypotenuse
⇒ sin θ = AB/AC = 2/√5
In right angled ∆ABC
tan θ = perpendicular/base
⇒ tan θ = AB/BC = 2/1
sin2 θ + tan2 θ = (2/√5)2 + (2/1)2
= 4/5 + 4/1
Taking LCM
= (4 + 20)/5
= 24/5
= 4 4/5
(c) (i) In ∆ABC
AD is perpendicular to BC
BD = 15 cm
sin B = 4/5
tan C = 1
In ∆ABD
sin B = perpendicular/hypotenuse
⇒ sin B = AD/AB = 4/5
Consider AD = 4x and AB = 5x
In right angled ∆ABD,
AB2 = AD2 + BD2
BD2 = AB2 – AD2
(15)2 = (5x)2 – (4x)2
⇒ 225 = 25x2 – 16x2
225 = 9x2
⇒ x2 = 225/9 = 25
x = √25 = 5
AD = 4 × 5 = 20
AB = 5 × 5 = 25
In right angled ∆ACD
tan C = perpendicular/base
tan C = AD/CD = 1/1
Consider AD = X then CD = x
In right angled ∆ADC
AC2 = AD2 + CD2
AC2 = x2 + x2 …(1)
So the equation becomes
AC2 = 202 + 202
⇒ AC2 = 400 + 400 = 800
AC = √800 = 20√2
Length of AD = 20 cm
Length of AB = 25 cm
Length of DC = 20 cm
Length of AC = 20√2 cm
(ii) In right angled ∆ABD
tan B = perpendicular/base
tan B = AD/BD
Substituting the values
tan B = 20/15 = 4/3
In right angled ∆ABD,
cos B = base/hypotenuse
cos B = BD/AB
Substituting the values
cos B = 15/25 = 3/5
Here,
LHS = tan2 B – 1/cos2 B
= (4/3)2 – 1/(3/5)2
= (4)2/(3)2 – (5)2/(3)2
= 16/9 – 25/9
So we get
= (16 – 25)/9
= -9/9
= – 1
= RHS
Hence, proved.
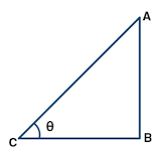
Question 9. If sin θ =3/5 and θ is acute angle, find
(i) cos θ
(ii) tan θ.
Answer :
Let ∆ ABC be a right angled at B
Let ∠ACB = θ
sin θ = 3/5
AB/AC = 3/5
Let AB = 3x
then AC = 5x
In right angled ∆ ABC,
(5x)2 = (3x)2 + BC2
⇒ BC2 = (5x)2 – (3x)2
⇒ BC2 = (2x)2
⇒ BC = 4x
(i) cos θ = Base/ Hypotenuse
= BC / AC
= 4x /5x
= 4/5
(ii) tan θ = perpendicular/Base
= AB/BC
= 3x/4x
= ¾
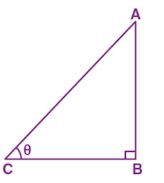
Question 10. Given that tan θ = 5/12 and θ is an acute angle, find sin θ and cos θ.
Answer :
Consider ∆ ABC be right angled at B and ∠ACB = θ
tan θ = 5/12
AB/BC = 5/12
Consider AB = 5x and BC = 12x
AC2 = AB2 + BC2
AC2 = (5x)2 + (12x)2
AC2 = 25x2 + 144x2 = 169x2
AC2 = (13x)2
⇒ AC = 13x
In right angled ∆ ABC
sin θ = perpendicular/hypotenuse
sin θ = AB/AC = 5x/13x = 5/13
In right angled ∆ ABC
cos θ = base/hypotenuse
So we get
cos θ = BC/AC
cos θ = 12x/13x
= 12/13
Question 11. If sin θ = 6/10, find the value of cos θ + tan θ.
Answer :
Consider ∆ ABC be right angled at B and ∠ACB = θ
It is given that
sin θ = AB/AC
⇒ sin θ = 6/10
Take AB = 6x then AC = 10x
In right angled ∆ ABC
AC2 = AB2 + BC2
(10x)2 = (6x)2 + BC2
BC2 = 100x2 – 36x2 = 64x2
BC2 = (8x)2
⇒ BC = 8x
In right angled ∆ ABC
cos θ = base/hypotenuse
⇒ cos θ = BC/AC
cos θ = 8x/10x = 4/5
In right angled ∆ ABC
tan θ = perpendicular/base
⇒ tan θ = AB/BC
tan θ = 6x/8x = ¾
Here
cos θ + tan θ = 4/5 + ¾
Taking LCM
= (16 + 15)/ 20
= 31/20
= 1 (11/20)
(ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths)
Question 12. If tan = 4/3, find the value of sin θ + cos θ (both sin θ and cos θ are positive).
Answer :
Let ∆ABC be a right angled
∠ACB = θ
Given that, tan θ = 4/3
(AB/BC = 4/3)
tan θ = 4/3
(AB/BC = 4/3)
Let AB = 4x,
then BC = 3x
In right angled ∆ABC
AC2 = AB2 + BC2
⇒ AC2 = AB2 + BC2
⇒ AC2 = AB2 + BC2
⇒ AC2 = AB2 + BC2
⇒ (AC2 = (4x)2 + (3x)2
⇒ AC2 = 16x2 + 9x2
⇒ AC2 = 25x2
⇒ AC2 = (5x)2
⇒ AC = 5x
Sin θ = perpendicular/Hypotenuse
= AB/AC
= 4x/5x
= 4/5
cos θ = Base/Hypotenuse
= BC/AC
= 3x/5x
= 3/5
sin θ + cos θ
= 4/5 + 3/5
= (4 + 3)/5
= 7/5
Hence,
Sin θ + cos θ = 7/5 = 1 2/5
Question 13. If cosec = √5 and θ is less than 90°, find the value of cot θ – cos θ.
Answer :
Given cosec θ = √5/1 = OP/PM
OP = √5 and PM = 1
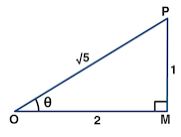
Now OP2 = OM2 + PM2
(√5)2 = OM2 + 12
⇒ 5 = OM2 + 1
⇒ OM2 = 5 – 1
⇒ OM2 = 4
⇒ OM = 2
Now cot θ = OM/PM
= 2/1
= 2
cos θ = OM/OP
= 2/√5
cot θ – cos θ = 2 – (2/√5)
= 2 (√5 – 1)/ √5
Question 14. Given sin θ = p/q, find cos θ + sin θ in terms of p and q.
Answer :
Given that sin θ = p/q
AB/AC = p/q
Let AB = px
And then AC = qx
In right angled triangle ABC
AC2 = AB2 + BC2
⇒ BC2 = AC2 – AB2
⇒ BC2 = q2x2 – p2x2
⇒ BC2 = (q2 – p2)x2
⇒ BC = √( q2 – p2)x
In right angled triangle ABC,
cos θ = base/hypotenuse
= BC/AC
= √( q2 – p2)x/qx
= √( q2 – p2)/q
Now,
Sin θ + cos θ = p/q + √(q2–p2)/q
= [p + √(q2–p2)]/q
Question 15. If θ is an acute angle and tan = 8/15, find the value of sec θ + cosec θ.
Answer :
Given tan θ = 8/15
θ is an acute angle
in the figure triangle OMP is a right angled triangle,
∠M = 90o and ∠Q = θ
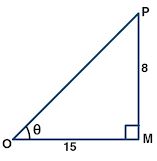
tanθ = PM/OL = 8/15
PM = 8, OM = 15
But OP2 = OM2 + PM2 using Pythagoras theorem,
= 152 + 82
= 225 + 64
= 289
= 172
OP = 17
sec θ = OP/OM = 17/15
cosec θ = OP/PM = 17/8
Now,
sec θ + cosec θ = (17/15) + (17/8)
= (136 + 255)/120
= 391/120
= 3 (31/120)
Question 16. Given A is an acute angle and 13 sin A = 5, Evaluate:
(5 sin A – 2 cos A)/ tan A.
Answer :
Let triangle ABC be a right angled triangle at B and A is an acute angle
Given that 13 sin A = 5
Sin A = 5/13
AB/AC = 5/13
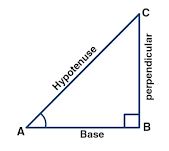
Let AB = 5x
AC = 13 x
In right angled triangle ABC,
AC2 = AB2 + BC2
⇒ BC2 = AC2 – BC2
⇒ BC2 = (13x)2 – (5x)2
⇒ BC2 = 169x2 – 25x2
⇒ BC2 = 144x2
⇒ BC = 12x
⇒ sin A = 5/13
⇒ cos A = base/ hypotenuse
= BC/AC
= 12x/ 13x
= 12/13
Tan A = perpendicular/ base
= AB/BC
= 5x/ 12x
= 5/ 12
(5 sin A – 2 cos A)/tan A = [(5) (5/13) – (2) (12/13)]/(5/12)
= (1/13)/(5/12)
= 12/65
Hence,
(5 sin A – 2 cos A)/tan A = 12/65
Question 17. Given A is an acute angle and cosec A = √2, find the value of
(2 sin2 A + 3 cot2 A)/ (tan2 A – cos2 A).
Answer :
Let triangle ABC be a right angled at B and A is a acute angle.
Given that cosec A = √2
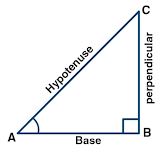
AC/BC = √2/1
Let AC = √2x
Then BC = x
In right angled triangle ABC
AC2 = AB2 + BC2
⇒ (√2x)2 = AB2 + x2
⇒ AB2 = 2x2 – x2
⇒ AB = x
sin A = perpendicular/ hypotenuse
= BC/AC
= 1/ √2
cot A = base/ perpendicular
= x/x
= 1
Tan A = perpendicular/ base
= BC/AB
= x/x
= 1
cos A = base/ hypotenuse
= AB/AC
= x/ √2x
= 1/√2
2 sin2A + 3 cot2A/(tan2A – cos2A) = 8
Trigonometrical Ratios Exercise-17
ML Aggarwal Class 9 ICSE Maths Solutions
Page 415
Question 18. The diagonals AC and BD of a rhombus ABCD meet at O. If AC = 8 cm and BD = 6 cm, find sin ∠OCD.
Answer :
Diagonals AC and BD of rhombus ABCD meet at O
AC = 8 cm and BD = 6 cm
O is the mid point of AC
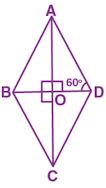
AO = OC = AC/2 = 8/2 = 4 cm
O is the mid point of BD
BO = OD = BD/2 = 6/2 = 3 cm
In right angled ∆COD
CD2 = OC2 + OD2
CD2 = 42 + 32
CD2 = 16 + 9 = 25
⇒ CD2 = 52
⇒ CD = 5 cm
In right angled ∆COD
sin ∠OCD = perpendicular/ hypotenuse
sin ∠OCD = OD/CD = 3/5
(ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths)
Question 19. If tan θ = 5/12, find the value of (cos θ + sin θ)/(cos θ – sin θ).
Answer :
Consider ∆ABC be right angled at B and ∠ACB = θ
tan θ = AB/BC = 5/12
Take AB = 5x then BC = 12x
In right angled ∆ABC,
AC2 = AB2 + BC2
AC2 = (5x)2 + (12x)2
AC2 = 25x2 + 144x2 = 169x2
AC2 = (13x)2
⇒ AC = 13x
In right angled ∆ABC
cos θ = base/hypotenuse
cos θ = BC/AC
cos θ = 12x/13x = 12/13
In right angled ∆ABC
sin θ = perpendicular/hypotenuse
⇒ sin θ = AB/AC
sin θ = 5x/13x = 5/13
(cos θ + sin θ)/(cos θ – sin θ) = [12/13 + 5/13]/ [12/13 – 5/13]
Taking LCM
= [(12 + 5)/13]/[(12 – 5)/13]
= (17/13)/(7/13)
= 17/13 × 13/7
= 17/7
Hence,
(cos θ + sin θ)/(cos θ – sin θ) = 17/7
Question 20. Given 5 cos A – 12 sin A = 0, find the value of (sin A + cos A)/ (2 cos A – sin A).
Answer :
5 cos A – 12 sin A = 0
We can write it as
5 cos A = 12 sin A
So we get
sin A/cos A = 5/12
sin A/ cos A = tan A
tan A = 5/12
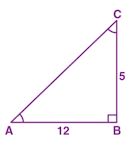
Consider ∆ABC right angled at B and ∠A is acute angle
tan A = BC/AB = 5/12
Take BC = 5x then AB = 12x
In right angled ∆ABC
AC2 = BC2 + AB2
AC2 = (5x)2 + (12x)2
⇒ AC2 = 25x2 + 144x2 = 169x2
AC2 = (13x)2
⇒ AC = 13x
In right angled ∆ABC
sin A = perpendicular/hypotenuse
sin A = BC/AC = 5x/13x = 5/13
In right angled ∆ABC
cos A = base/hypotenuse
⇒ cos A = AB/AC = 12x/13x = 12/13
(sin A + cos A)/(2 cos A – sin A) = [(5/13) + (12/13)]/[(2× 12/13) – 5/13]
= [(5+12)/13]/[24/13 – 5/13]
= [(5+12)/13]/[(24 – 5)/13]
= (17/13)/(19/13)
= 17/13 × 13/19
= 17/19
Hence, (sin A + cos A)/ (2 cos A – sin A) = 17/19
Question 21. If tan θ = p/q, find the value of (p sin θ – q cos θ)/ (p sin θ + q cos θ).
Answer :
tan θ = p/q
Consider ∆ABC be right angled at B and ∠BCA = θ
tan θ = BC/AB = p/q
BC = px then AB = qx
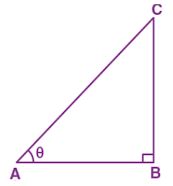
AC2 = BC2 + AB2
AC2 = (px)2 + (qx)2
⇒ AC2 = p2x2 + q2x2
⇒ AC2 = x2 (p2 + q2)
AC = √x2 (p2 + q2)
⇒ AC = x(√p2 + q2)
In right angled ∆ABC
sin θ = perpendicular/hypotenuse
⇒ sin θ = BC/AC
sin θ = px/x(√p2 + q2)
sin θ = p/(√p2 + q2)
In right angled ∆ABC
cos θ = base/hypotenuse
⇒ cos θ = AB/AC
cos θ = qx/x(√p2 + q2)
cos θ = q/(√p2 + q2)

Question 22. If 3 cot θ = 4, find the value of (5 sinθ – 3 cosθ)/(5 sinθ + 3 cosθ).
Answer :
3 cot θ = 4
⇒ cot θ = 4/3
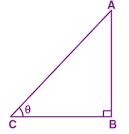
Consider ∆ABC be right angled at B and ∠ACB = θ
cot θ = BC/AB = 4/3
Take BC = 4x then AB = 3x
In right angled ∆ABC
AC2 = AB2 + BC2
AC2 = (3x)2 + (4x)2
⇒ AC2 = 9x2 + 16x2 = 25x2
AC2 = (5x)2
⇒ AC = 5x
In right angled ∆ABC
sin θ = perpendicular/hypotenuse
⇒ sin θ = AB/AC
sin θ = 3x/5x = 3/5
In right angled ∆ABC
cos θ = base/hypotenuse
⇒ cos θ = BC/AC
cos θ = 4x/5x
= 4/5
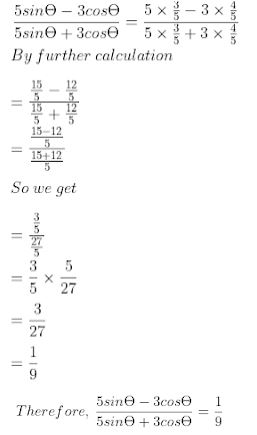
(ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths)
Question 23.
(i) If 5 cosθ – 12 sinθ = 0, find the value of (sin θ + cos θ)/(2 cosθ – sinθ).
(ii) If cosecθ = 13/12, find the value of (2 sinθ – 3 cosθ)/(4 sinθ – 9 cosθ).
Answer :
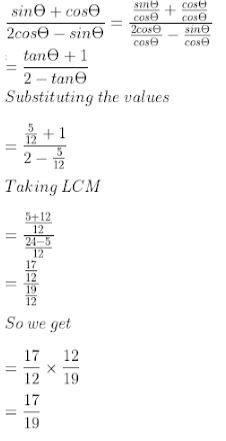
(i) 5 cosθ – 12 sinθ = 0
5 cosθ = 12 sinθ
⇒ sin θ/cos θ = 5/12
⇒ tan θ = 5/12
Dividing both numerator and denominator by cos θ
(ii) cosec θ = 13/12
cosec θ = 1/sin θ
1/sin θ = 13/12
⇒ sin θ = 12/13
Here cos2 θ = 1 – sin2 θ
= 1 – (12/13)2
= 1 – 144/169
Taking LCM
= (169 – 144)/ 169
= 25/169
= (5/13)2
cos θ = 5/13
Here,
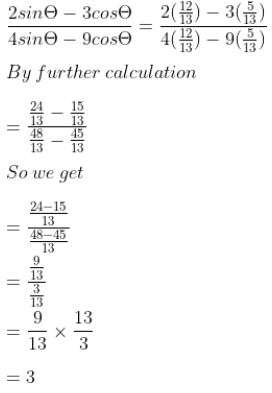
Question 24. If 5 sin θ = 3, find the value of (secθ – tanθ)/(secθ + tanθ).
Answer :
Consider ∆ABC be right angled at B and ∠ACB = θ
5 sin θ = 3
sin θ = AB/AC = 3/5
Take AB = 3x then AC = 5x
In right angled ∆ABC
AC2 = AB2 + BC2
⇒ BC2 = AC2 – AB2
BC2 = (5x)2 – (3x)2
BC2 = 25x2 – 9x2 = 16x2
⇒ BC2 = (4x)2
⇒ BC = 4x
In right angled ∆ABC
sec θ = hypotenuse/base
⇒ sec θ = AC/BC = 5x/4x = 5/4
In right angled ∆ABC
tan θ = perpendicular/base
⇒ tan θ = AB/BC = 3x/4x = ¾
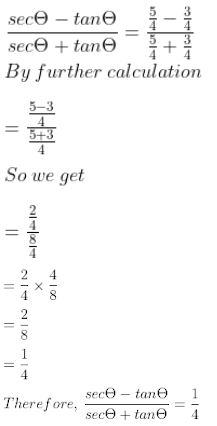
(ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths)
Question 25. If θ is an acute angle and sin θ = cos θ, find the value of 2 tan2 θ + sin2 θ – 1.
Answer :
Consider ∆ABC be right angled at B and ∠ACB = θ
sin θ = cos θ
⇒ sin θ/cos θ = 1
tan θ = AB/BC = 1
Take AB = x then BC = x
In right angled ∆ABC,
AC2 = AB2 + BC2
⇒ AC2 = x2 + x2 = 2x2
AC = √2x2
⇒ AC = (√2)x
In right angled ∆ABC
sin θ = perpendicular/hypotenuse
sin θ = AB/AC = x/√2x = 1/√2
Here
2 tan2 θ + sin2 θ – 1 = 2×(1)2 + (1/√2)2 – 1
= (2×1) + ½ – 1
= 2 + ½ – 1
= 1+ ½
Taking LCM
= (2 + 1)/2
= 3/2
Hence, 2 tan2 θ + sin2 θ – 1 = 3/2.
Question 26. Prove the following:
(i) cos θ tan θ = sin θ
(ii) sin θ cot θ = cos θ
(iii) sin2 θ/ cos θ + cos θ = 1/ cos θ.
Answer :
(i) cos θ tan θ = sin θ
LHS = cos θ tan θ
tan θ = sin θ/cos θ
= cos θ (sin θ/cos θ)
= 1× sin θ/1
= sin θ
= RHS
Hence, LHS = RHS.
(ii) sin θ cot θ = cos θ
LHS = sin θ cot θ
cot θ = cos θ/sin θ
= sin θ (cos θ/sin θ)
= 1× cos θ/1
= cos θ
= RHS
Hence, LHS = RHS.
(iii) sin2θ/cosθ + cosθ = 1/cosθ
LHS = sin2θ/cosθ + cosθ/1
Taking LCM
= (sin2θ + cos2θ)/cosθ
sin2θ + cos2θ = 1
= 1/cos θ
= RHS
Hence,
LHS = RHS.
Question 27. If in ∆ABC, ∠C = 90° and tan A = ¾, prove that sin A cos B + cos A sin B = 1.
Answer :
tan A = BC/AC = ¾
AB2 = AC2 + BC2
= 42 + 32
= 16 + 9
= 25
= 52
AB = 5
sin A = BC/AC = 3/5
cos A = AC/AB = 4/5
cos B = BC/AB = 3/5
sin B = AC/AB = 4/5
LHS = sin A cos B + cos A sin B
= (3/5 × 3/5) + (4/5 × 4/5)
= 9/25 + 16/25
= (9 + 16)/ 25
= 25/25
= 1
= RHS
Hence, LHS = RHS.
(ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths)
Question 28.
(a) In figure (1) given below, ∆ABC is right-angled at B and ∆BRS is right-angled at R. If AB = 18 cm, BC = 7.5 cm, RS = 5 cm, ∠BSR = x° and ∠SAB = y°, then find:
(i) tan x°
(ii) sin y°.
(b) In the figure (2) given below, ∆ABC is right angled at B and BD is perpendicular to AC. Find
(i) cos ∠CBD
(ii) cot ∠ABD.
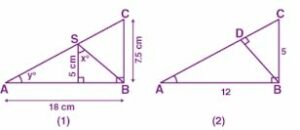
Answer :
(a) ∆ABC is right-angled at B, ∆BSC is right-angled at S and ∆BRS is right-angled at R
AB = 18 cm, BC = 7.5 cm, RS = 5 cm, ∠BSR = x° and ∠SAB = y°
By Geometry ∆ARS and ∆ABC are similar
AR/AB = RS/BC
AR/18 = 5/7.5
AR = (5×18)/7.5 = (1×18)/1.5
Multiply both numerator and denominator by 10
AR = (18×10)/15
⇒ AR = (10×6)/5
⇒ AR = (2×6)/1 = 12
RB = AB – AR
⇒ RB = 18 – 12 = 6
In right angled ∆ABC
AC2 = AB2 + BC2
AC2 = 182 + 7.52
AC2 = 324 + 56.25 = 380.25
⇒ AC = √380.25 = 19.5 cm
(i) In right angled ∆BSR
tan x° = perpendicular/base
tan x° = RB/RS = 6/5
(ii) In right angled ∆ASR
sin y° = perpendicular/hypotenuse
AS2 = 122 + 52
AS2 = 144 + 25 = 169
⇒ AS = √169 = 13 cm
sin y° = RS/AS = 5/13
(b) ∆ABC is right angled at B and BD is perpendicular to AC
In right angled ∆ABC
AC2 = AB2 + BC2
AC2 = 122 + 52
AC2 = 144 + 25 = 169
AC2 = (13)2
⇒ AC = 13
By Geometry ∠CBD = ∠A and ∠ABD = ∠C
(i) cos ∠CBD = cos ∠A = base/hypotenuse
In right angled ∆ABC
cos ∠CBD = cos ∠A = AB/AC = 12/13
(ii) cos ∠ABD = cos ∠C = base/perpendicular
In right angled ∆ABC
cos ∠ABD = cos ∠C = BC/AB = 5/12
Trigonometrical Ratios Exercise-17
ML Aggarwal Class 9 ICSE Maths Solutions
Page 416
Question 29. In the adjoining figure, ABCD is a rectangle. Its diagonal AC = 15 cm and ∠ACD = α. If cot α = 3/2, find the perimeter and the area of the rectangle.
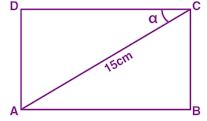
Answer :
In right ∆ADC
cot α = CD/AD = 3/2
Take CD = 3x then AD = 2x
AC2 = CD2 + AD2
(15)2 = (3x)2 + (2x)2
13x2 = 225
⇒ x2 = 225/13
x = √225/13 = 15/√13
Length of rectangle (l) = 3x = (3 × 15)/ √13 = 45/√13 cm
Breadth of rectangle (b) = 2x = (2×15)/√13 = 30/√13 cm
(i) Perimeter of rectangle = 2 (l + b)
= 2 (45/√13 + 30/√13)
So we get
= 2 × 75/√13
= 150/√13 cm
(ii) Area of rectangle = l × b
Substituting the values of l and b
= 45/√13 × 30/√13
= 1350/13
= 103 (11/13) cm2
Question 30. Using the measurements given in the figure alongside,
(a) Find the values of:
(i) sin ϕ
(ii) tan θ.
(b) Write an expression for AD in terms of θ.
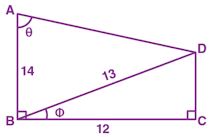
Answer :
BC = 12, BD = 13
In right angled ∆BCD
BD2 = BC2 + CD2
CD2 = BD2 – BC2
CD2 = (13)2 – (12)2
⇒ CD2 = 169 – 144 = 25
CD = √25 = 5
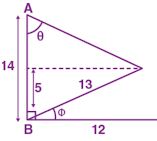
CD = BE = 5 and EA = AE = 14 – 5 = 9
(a)
(i) sin ϕ = perpendicular/hypotenuse
In right angled ∆BCD
sin ϕ = CD/BD = 5/13
(ii) tan θ = perpendicular/hypotenuse
In right angled ∆AED
tan θ = ED/AE = BC/AE = 12/9 = 4/3 (Since ED = BC)
(b) In right angled ∆AED
sin θ = perpendicular/hypotenuse
cos θ = base/perpendicular
sin θ = ED/AD or cos θ = AE/AD
AD = ED/sin θ or AD = AE/cos θ
AD = 12/sin θ or AD = 9/cos θ
Hence,
AD = 12/ sin θ or AD = 9/cos θ.
Question 31. Prove the following:
(i) (sin A + cos A)2 + (sin A – cos A)2 = 2
(ii) cot2 A – 1/sin2 A + 1 = 0
(iii) 1/(1 + tan2 A) + 1/(1 + cot2 A) = 1
Answer :
(i) (sin A + cos A)2 + (sin A – cos A)2 = 2
LHS = (sin A + cos A)2 + (sin A – cos A)2
(a + b)2 = a2 + b2 + 2ab and (a – b)2 = a2 + b2 – 2ab
= [(sin A)2 + (cos A)2 + 2 sin A cos A] + [(sin A)2 + (cos A)2 – 2 sin A cos A]
= sin2 A + cos2 A + 2 sin A cos A + sin2 A + cos2 A – 2 sin A cos A
= sin2 A + cos2 A + sin2 A + cos2 A
= 2 sin2 A + 2 cos2 A
sin2 A + cos2 A = 1
= 2 (sin2 A + cos2 A)
= 2 (1)
= 2
= RHS
Hence, LHS = RHS.
(ii) cot2 A – 1/sin2 A + 1 = 0
LHS = cot2 A – 1/sin2 A + 1
1/sin A = cosec A
= cot2 A – cosec2 A + 1
= (1 + cot2 A) – cosec2 A
1 + cot2 A = cosec2 A
= cosec2 A – cosec2 A
= 0
= RHS
Hence, LHS = RHS.
(iii) 1/(1 + tan2 A) + 1/(1 + cot2 A) = 1
LHS = 1/(1 + tan2 A) + 1/(1 + cot2 A)
sec2 A – tan2 A = 1
⇒ sec2 A = 1 + tan2 A
⇒ cosec2 A – cot2 A = 1
⇒ cosec2 A = 1 + cot2 A
= 1/sec2 A + 1/cosec2 A
1/sec A = cos A and 1/cosec A = sin A
= cos2 A + sin2 A
= 1
= RHS
Hence,
LHS = RHS.
Question 32. Simplify…………
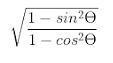
Answer :
1 = sin2 θ + cos2 θ
= √cos2 θ/sin2 θ
= cos θ/ sin θ
Here cos θ/sin θ = cot θ
= cot θ
Hence,
![]()
Question 33. If sin θ + cosec θ = 2, find the value of sin2 θ + cosec2 θ.
Answer :
sin θ + cosec θ = 2
⇒ sin θ + 1/sin θ = 2
sin2 θ + 1 = 2 sin θ
⇒ sin2 θ – 2 sin θ + 1 = 0
(sin θ – 1)2 = 0
⇒ sin θ – 1 = 0
⇒ sin θ = 1
sin2 θ + cosec2 θ = sin2 θ + 1/sin2 θ
= 12 + 1/12
= 1 + 1/1
= 1 + 1
= 2
(ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths)
Question 34. If x = a cos θ + b sin θ and y = a sin θ – b cos θ, prove that x2 + y2 = a2 + b2.
Answer :
x = a cos θ + b sin θ …(1)
y = a sin θ – b cos θ …(2)
By squaring and adding both the equations
x2 + y2 = (a cos θ + b sin θ)2 + (a sin θ – b cos θ)2
(a + b)2 = a2 + b2 + 2ab and (a – b)2 = a2 + b2 – 2ab
= [(a cosθ)2 + (b sinθ)2 + 2 (a cosθ) (b sinθ)] + [(a sinθ)2 + (b cosθ)2 – 2 (a sinθ) (b cosθ)]
= a2 cos2θ + b2 sin2θ + 2 ab sinθ cosθ + a2 sin2θ + b2 cos2θ – 2 ab sinθ cosθ
= a2 cos2θ + b2 sin2θ + a2 sin2θ + b2 cos2θ
= a2 (cos2θ + sin2θ) + b2 (sin2θ + cos2θ)
Here sin2θ + cos2θ = 1
= a2 (1) + b2 (1)
= a2 + b2
Hence, x2 + y2 = a2 + b2.
— : End of ML Aggarwal Trigonometrical Ratios Exe-17 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends
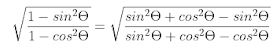

Jo bi ye join group hilata hai usko plz bnd kroo isse