ML Aggarwal Quadrilaterals Shapes Exe-13.1 Class 8 ICSE Ch-13 Maths Solutions

ML Aggarwal Quadrilaterals Shapes Exe-13.1 Class 8 ICSE Ch-13 Maths Solutions. We Provide Step by Step Answer of  Exe-13.1 Questions for Quadrilaterals Shapes as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.

ML Aggarwal Quadrilaterals Shapes Exe-13.1 Class 8 ICSE Maths Solutions

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	8th
Chapter-13	Quadrilaterals Shapes
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Exe-13.1 Questions
Edition	2023-2024

Quadrilaterals Shapes Exe-13.1

ML Aggarwal Class 8 ICSE Maths Solutions

Page-232

Question 1. Some figures are given below.

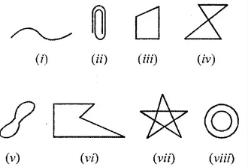
Classify each of them on the basis of the following:
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon

Answer:

(a) (i), (ii), (iii), (v) and (vi) are simple curves.
(b) (iii), (v), (vi) are simple closed curves.
(c) (iii) and (vi) are polygons.
(d) (iii) is a convex polygon.
(e) (v) is a concave polygon.

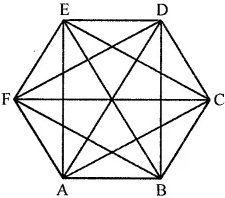
Question 2. How many diagonals does each of the following have?

(a) A convex quadrilateral
(b) A regular hexagon

Answer:

(a) A convex quadrilateral: It has two diagonals.
(b) A regular hexagon: It has 9 diagonals as shown.

Question 3. Find the sum of measures of all interior angles of a polygon with number of sides:

(i) 8
(ii) 12

Answer:

(i) Sum of measures of all interior angles of
8-sided polygon = (2n – 4) × 90°
= (2 × 8 – 4) × 90°
= 12 × 90° = 1080°
(ii) Sum of measures of all interior angles of
12-sided polygon = (2n – 4) × 90°
= (2 × 12 – 4) × 90°
= 18 × 90°= 1800°

Question 4. Find the number of sides of a regular polygon whose each exterior angles has a measure of

(i) 24°
(ii) 60°
(iii) 72°

Answer:

(i) Let number of sides of the polygon = n
Each exterior angle = 24°
∴ n = 360°/24° = 15 sides
∴ Polygon is of 15 sides.
(ii) Each interior angle of the polygon = 60°
Let number of sides of the polygon = n
∴ n = 360°/60° = 6
∴ Number of sides = 6
(iii) Each interior angle of the polygon = 72°
Let number of sides of the polygon = n
∴ n = 360°/72° = 5
∴ Number of sides = 5

Question 5. Find the number of sides of a regular polygon if each of its interior angles is

(i) 90°
(ii) 108°
(iii) 165°

Answer:

(i) The number of sides of a regular polygon whose each interior angles has a measure of 90^o

Let us assume the number of sides of the regular polygon be n,

Then, we know that 90^o = ((2n – 4)/n) × 90^o

90^o/90^o = (2n – 4)/n

1 = (2n – 4)/n

2n – 4 = n

2n – n = 4

n = 4

Hence, the number of sides of a regular polygon is 4.

(ii) The number of sides of a regular polygon whose each interior angles has a measure of 108^o

Let us assume the number of sides of the regular polygon be n,

Then, we know that 108^o = ((2n – 4)/n) × 90^o

108^o/90^o = (2n – 4)/n

6/5 = (2n – 4)/n

5(2n – 4) = 6n

10n – 20 = 6n

10n – 6n = 20

4n = 20

n = 20/4

n = 5

Hence, the number of sides of a regular polygon is 5.

So, it is a Pentagon.

(iii) The number of sides of a regular polygon whose each interior angles has a measure of 165^o

Let us assume the number of sides of the regular polygon be n,

Then, we know that 165^o = ((2n – 4)/n) × 90^o

165^o/90^o = (2n – 4)/n

11/6 = (2n – 4)/n

6(2n – 4) = 11n

12n – 24 = 11n

12n – 11n = 24

n = 24

Hence, the number of sides of a regular polygon is 24.

Question 6. Find the number of sides in a polygon if the sum of its interior angles is:

(i) 1260°
(ii) 1980°
(iii) 3420°

Answer:

We know that, sum of interior angles of polygon
is given by (2n – 4) at right angles.
(i) 1260°
∴ 1260 = (2n – 4) × 90
⇒ 1260/90 = 2n – 4
⇒ 14 = 2n – 4
⇒ n = 9
(ii) 1980°
∴ 1980 = (2n – 4) × 90
⇒ 1980/90 = 2n – 4
⇒ 22 = 2n – 4
⇒ n = 13.
(iii) 3420°
∴ 3420 = (272 – 4) × 90 3420
⇒ 3420/90 = 2n – 4
⇒ 38 = 2n – 4
⇒ n = 21

Question 7. If the angles of a pentagon are in the ratio 7 : 8 : 11 : 13 : 15, find the angles.

Answer:

Ratio in the angles of a polygon = 7 : 8 : 11 : 13 : 15
Sum of angles of a pentagon = (2n – 4) × 90°
= (2 × 5 – 4) × 90°
= 6 × 90° = 540°
Let the angles of the pentagon be
7x, 8x, 11x, 13x, 15x
∴ 7x + 8x + 11x + 13x + 15x = 540°
⇒ 54x = 540° ⇒ x = 540°/54 = 10°
∴ Angles are 7 × 10° = 70°, 8 × 10° = 80°,
11 × 10° = 110°, 13 × 10° = 130° and 15 × 10°= 150°
∴ Angles are 70°, 80°, 110°, 130° and 150°

Question 8. The angles of a pentagon are x°, (x – 10)°, (x + 20)°, (2x – 44)° and (2x – 70°) Calculate x.

Answer:

Angles of a pentaon are x°, (x – 10)°, (x + 20)°,
(2x – 44)° and (2x – 70°)
But sum of angles of a pentagon
= (2n – 4) × 90°
= (2 × 5 – 4) × 90°
= 6 × 90° = 540°
∴ x + x – 10° + x + 20° + 2x – 44° + 2x – 70° = 540°
⇒ 7x – 104° = 540°
⇒ 7x = 540° + 104° = 644°
⇒ x = 644°/7 = 92°
∴ x = 92°

(ML Aggarwal Quadrilaterals Shapes Exe-13.1 Class 8 ICSE Maths)

Question 9. The exterior angles of a pentagon are in ratio 1 : 2 : 3 : 4 : 5. Find all the interior angles of the pentagon.

Answer:

Let the exterior angles of the pentagon are x, 2x, 3x, 4x and 5x.
We know that sum of exterior angles of polygon is 360°.
∴ x + 2x + 3x + 4x + 5x = 360°
⇒ 15x = 360°
⇒ x = 360°/15
⇒ x = 24°
∴ Exterior angles are 24°, 48°, 72°, 96°, 120°
Interior angles are 180° – 24°, 180° – 48°, 180° – 72°, 180° – 96°,
180° – 120° i.e. 156°, 132°, 108°, 84°, 60°.

Question 10. In a quadrilateral ABCD, AB || DC. If ∠A : ∠D = 2:3 and ∠B : ∠C = ∠7 : 8, find the measure of each angle.

Answer:

In a quadrilateral ABCD, AB || DC. If ∠A : ∠D = 2:3 and ∠B : ∠C = ∠7 : 8,

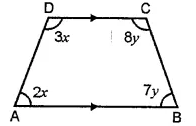
∠A + ∠D = 180^o

Let us assume the angle ∠A = 2a and ∠D = 3a

2a + 3a = 180^o

5a = 180^o

a = 180^o/5

a = 36^o

∠A = 2a = 2 × 36^o = 72^o

∠D = 3a = 3 × 36^o = 108^o

Now, ∠B + ∠C = 180^o

Let us assume the angle ∠B = 7b and ∠C = 8b

7b + 8b = 180^o

15b = 180^o

b = 180^o/15

b = 12^o

∠B = 7b = 7 × 12^o = 84^o

∠C = 8b = 8 × 12^o = 96^o

Question 11. From the adjoining figure, find

(i) x
(ii) ∠DAB
(iii) ∠ADB

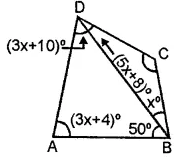
Answer:

(i) ABCD is a quadrilateral
∴ ∠A + ∠B + ∠C + ∠D = 360°
⇒ (3x + 4) + (50 + x) + (5x + 8) + (3x + 10) = 360
⇒ 3x + 4 + 50 + x + 5x + 8 + 3x + 10 = 360°
⇒ 12x + 72 = 360°
⇒ 12x = 288
⇒ x = 24
(ii) ∠DAB = (3x + 4) = 3 × 24 + 4 = 76°
(iii) ∠ADB = 180°- (76° + 50°) = 54° (∵ ABD is a ∆)

---

Quadrilaterals Shapes Exe-13.1

ML Aggarwal Class 8 ICSE Maths Solutions

Page-233

Question 12. Find the angle measure x in the following figures:

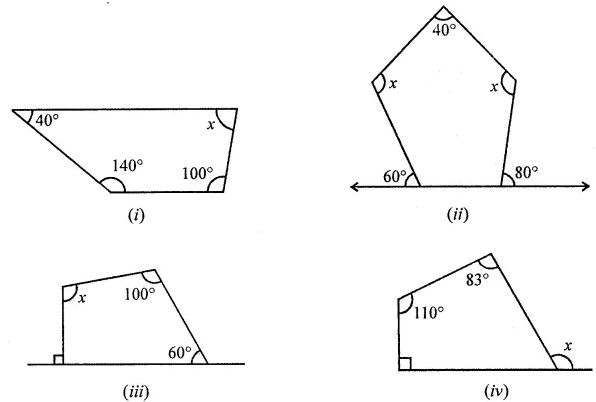
Answer:

(i) In quadrilateral three angles are 40°, 140° and 100°

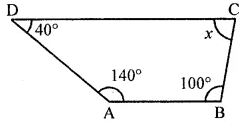
But sum of Four angles = 360°
⇒ 40° + 140°+ 100° + x = 360°
⇒ 280° + x = 360°
⇒ x = 360° – 280° = 80°
(ii) In the given figure, ABCDE is a pentagon.
Where side AB is produced to both sides0

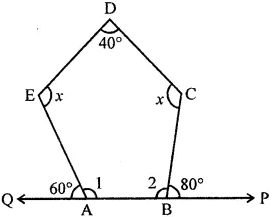
∠1 + 60° = 180° (Linear pair)
∠1 = 180°- 60°= 120°
Similarly ∠2 + 80° = 180°
∴ ∠2 = 180°- 80°= 100°
Now, sum of angles of a pentagon = (2n – 4) × 90°
= (2 × 5 – 4) × 90° = 6 × 90° = 540°
∴ ∠A + ∠B + ∠C + ∠D + ∠E = 540°
⇒ 120° + 100° + x + 40° + x = 540°
⇒ 260° + 2x = 540°
⇒ 2x = 540° – 260° = 280°
⇒ x = 280°/2 = 140°
(iii) In the given figure, ABCD is a quadrilateral
whose side AB is produced is both sides ∠A = 90°

But ∠A + ∠B + ∠C + ∠D = 360°
(Sum of angles of a quadrilateral)
⇒ 90°+ 60°+ 110° + x = 360°
⇒ 260° + x = 360°
⇒ x = 360° – 260° = 100°
∴ x = 100°
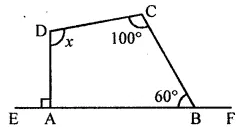
(iv) In the given figure, ABCD is a quadrilateral
whose side AB is produced to E.

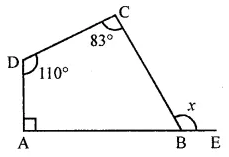
∠A = 90°, ∠C = 83°, ∠D = 110°
∠B + x = 180° (Lienar pair)
∠B = 180° – x
But ∠A + ∠B + ∠C + ∠D = 360°
⇒ 90° + (180° – x) + 83° + 110° = 360°
(Sum of angles of a quadrilateral)
⇒ 283°+ 180° – x = 360°
⇒ x = 283° + 180°- 360°
⇒ x = 463° – 360°= 103°

Question 13. A heptagon has three equal angles each of 120° and four equal angles. Find the size of equal angles.

Answer:

Sum of angles of a heptagon = (2 × n – 4) × 90°
= (2 × 7 – 4) × 90°
= 10 × 90° = 900°
Sum of three angles are each equal i.e. 120°
= 120° × 3 = 360°
Sum of remaining 4 equal angles
= 900° – 360° = 540°
∴ Each angle = 540°/4 = 135°

Question 14. The ratio between an exterior angle and the interior angle of a regular polygon is 1 : 5. Find

(i) the measure of each exterior angle
(ii) the measure of each interior angle
(iii) the number of sides in the polygon.

Answer:

Ratio between an exterior and an interior angle = 1 : 5
Let exterior angle = x
Then interior angle = 5x
But sum of interior angle and exterior angle = 180°
∴ x + 5x = 180°
⇒ 6x = 180°
⇒ 180°/6 = 30°
(i) Measure of exterior angle x = 30°
(ii) and measure of interior angle = 5x = 5 × 30° = 150°

(iii) the number of sides in the polygon

The number of sides of a regular polygon whose each interior angles has a measure of 150^o

Let us assume the number of sides of the regular polygon be n,

150^o = ((2n – 4)/n) × 90^o

150^o/90^o = (2n – 4)/n

5/3 = (2n – 4)/n

By cross multiplication,

3(2n – 4) = 5n

6n – 12 = 5n

6n – 5n = 12

n = 12

Therefore, the number of sides of a regular polygon is 12.

(ML Aggarwal Quadrilaterals Shapes Exe-13.1 Class 8 ICSE Maths)

Question 15. Each interior angle of a regular polygon is double of its exterior angle. Find the number of sides in the polygon.

Answer:

Each interior angle of a regular polygon is double of its exterior angle.

So, let us assume exterior angle be y

Interior angle be 2y,

sum of interior and exterior angle is equal to 180^o,

y + 2y = 180^o

3y = 180^o

y = 180^o/3

y = 60^o

interior angle = 2y = 2 × 60^o = 120^o

The number of sides of a regular polygon whose each interior angles has a measure of 120^o

Let us assume the number of sides of the regular polygon be n,

Then, we know that 120^o = ((2n – 4)/n) × 90^o

120^o/90^o = (2n – 4)/n

4/3 = (2n – 4)/n

By cross multiplication,

3(2n – 4) = 4n

6n – 12 = 4n

6n – 4n = 12

2n = 12

n = 12/2

n = 6

Hence, the number of sides of a regular polygon is 6.

— End of Quadrilaterals Shapes Exe-13.1 Class 8 ICSE Maths Solutions :–

Return to : – ML Aggarwal Maths Solutions for ICSE Class -8

Thanks