Uniform Circular Motion Numerical on Angular Velocity Centripetal Acceleration and Force ISC Nootan Physics Solutions Ch-8. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Uniform Circular Motion Numerical on Angular Velocity Centripetal Acceleration and Force
ISC Nootan Class 11 Solutions Kumar and Mittal Physics of Nageen Prakashan
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Writer | Kumar and Mittal |
| Publication | Nageen Prakashan |
| Chapter-8 | Uniform Circular Motion |
| Topics | Numerical on Angular Velocity Centripetal Acceleration and Force |
| Academic Session | 2024-2025 |
Numerical on Angular Velocity Centripetal Acceleration and Force
Ch-8 Uniform Circular Motion ISC Nootan Class 11 Solutions Kumar and Mittal Physics of Nageen Prakashan
Que-1: A particle moving on a circle has a velocity of 5 m/s and a normal acceleration of 10 m/s². Determine the radius of the circle.
Ans- a = v²/r
=> r = v²/a
=> 5 x 5 /10
=> 2.5 m
Que-2: A particle completes 4 revolution per second on a circular path of radius 0.25m. Calculate the angular velocity and the centripetal acceleration of the particle.
Ans- ω = 2 π n = 2 π x 4 = 8 π rad/sec
and a = rω² = 0.25 x (8π)²
=> 16 π² m/s²
Que-3: Calculate the average angular velocity and the average linear velocity of the tip of a 10 cm long second-hand of a watch.
Ans- ω = 2π/60 = π/30 rad/s
again v = r ω
=>10 x π/30
=>π/3 cm/s
Que-4: A particle is completing 5 revolutions per second in a circle of radius 6 cm. Calculate its linear velocity and the centripetal acceleration acting on it.
Ans- v = r ω
=> 0.06 x 2 x π x 5
=> 0.06 π m/s
a = r ω²
=> 0.06 x (2 π n)²
=> 0.06 x (2 π x 5)²
=> 6 π² m/s²
Que-5: A car is moving with a speed of 30 m/s on a circular track of radius 500 m. Its speed is increasing at a rate of 2.0 m/s². Determine the magnitude of its acceleration.
Ans- a = √at² = ar²
=> √ 2² + (30²/500)²
=> √4 + 81/25
=> 2.7 m/s²
Que-6: The second’s hand of a clock is 2.0 cm long. Calculate:
(i) the speed of the tip of the hand,
(ii) the velocity at 0.0 second and at 15 second,
(iii) the change in velocity from 0.0 to 15 second,
(iv) average acceleration.
Ans- (i) v = r ω
=> 2 x 2 π / 60
=> π/60
=> 0.21 cm/s
(ii) at 0.00 it will be horizontally right and at 15 s it is vertically downward.
(iii) Ι→ΔvΙ = √(21)² + (21)² = 0.21√2
=> 0.30 cm/s downwards at 45° towards left from the vertical
(iv) a = Δv / Δt
=> 0.30 /15
=> 0.02 cm/s² downwards at 45° towards left from the vertical.
Que-7: A stone of mass 0.1 kg tied to one end of a string 1.0 m long is revolved in a horizontal circle at the rate of 10/π revolutions per sec. Calculate the tension of the string.
Ans- Tension = Force
Force = mv²/r = m r² ω²/r
=> m r ω² = m r (2 π n)²
=> 0.1 x 1 x (2 π x 10/π)²
=> 40 N
Que-8: A particle of mass 2.0 x 10^-2 kg is moving with uniform speed of 4.0 m/s in circular path of radius 1.0 m. Find, with the help of a vector-diagram;
(i) the change in velocity (→VB – →VA) of the particle in moving from A to B,
(ii) the change in the centripetal force (→FB – →FA).
Ans-
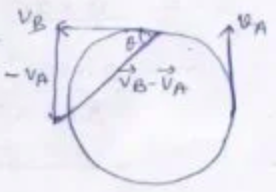
→vB – →vA = √(vB)² + (-vA)²
=>√(4)² + (-4)²
=>4√2
=> 5.7 m/s
and θ = 45°
Similarly
fB – fA = F√2
=> m v²/r . √2
=> 2 x 10^-2 x v²/1 x √2
=> 0.45 N
and θ = 45°
Que-9: Calculate the centripetal acceleration at a point on the equator of earth. The radius of earth is 6.4 x 10^6 m and it completes one rotation per day about its axis.
Ans- a = r ω²
=> r x (2 π/T)² ω = 2π/T
=> [6.4 x 10^6 x 4 x (3.14)²] / (24 x 60 x 60)²
=> 3.4 x 10^-2 m/s²
Que-10: The earth revolves around the sun in a circular path with a speed of 30 km/s. What is the radial acceleration directed towards the sun?
Ans- a = rω² = r ω . ω = v x 2π / T
=> (30 x 10³ x 2 x 3.14) / (365 x 24 x 60 x 60)
=> 5.97 x 10^-3 m/s²
Que-11: With what horizontal velocity should a body be thrown so that it may move parallel to the surface of the earth along the equator? The radius of the earth at the equator is 6400 km and g = 9.7 m/s².
Ans- g = v²/r
=> v = √g r
=> √9.8 x 6.4 x 10^6
=> ≈7879 m/s = 7.879 km/s
Que-12: An electron experiences a radial acceleration of 3 × 10^14 m/s² while moving in a magnetic field along a circle of radius 0.15 m. Calculate the speed of the electron.
Ans- a = v²/r
=> v = √r x a
=> v = √0.15 x 3 x 10^14
=>6.7 x10^6 m/s
Que-13: In hydrogen atom the electron revolves around the proton at a speed of 2.18 x 10^6 m/s in a circle of radius 5.28 × 10^-11 m. Calculate the acceleration of the electron and compare it with the acceleration due to gravity.
Ans- a = v²/r
=> (2.10 x 10^6)² / 5.20 x 10^-11
=> 9.0 x 10^22 m/s²
now a /g = 9.0 x 10^22 / 9.8 ≅10^22
Que-14: In a hydrogen atom, the electron revolves round the proton in a circular orbit of radius 0.528 Å with a speed of 2.18 x 10^6 m/s. Calculate the centripetal force acting on the electron. (Mass of electron = 9.1 x 10^-31 kg, 1 Å = 10^-10m).
Ans- F = mv²/r
=> 9.1 x 10^-31 x (2.18 x 10^6)² / 0.528 x 10^-10
=> 8.2 x 10^-8 N
Que-15: A particle of mass 1.6 x 10^-27 kg is revolving in a circular path of radius 10 cm under the influence of a centripetal force of 2.5 × 10^-12 N. Find out its angular velocity.
Ans- F =m r ω²
=> ω = √F/mr
=> √2.5 x 10^-12 / 1.6 x 10^-27 x 10 x 10^-2
=> 1.25 x 10^8 rad/s
Que-16: A particle of mass 5 g is moving in a circle of radius 0.5 m with an angular velocity of 6 rad/s. Find:
(i) the change in linear velocity in half a revolution,
(ii) the magnitude of the acceleration of the particle.
Ans- v = r ω
=> v = 6 x 0.5 = 3 m/s
change in velocity when particle turns through θ
Δv = 2 v sin θ/2
for semicircle θ = 180°
∴ Δv = 2 v sin 90°
=> 2 x 3
=> 6 m/s
a = v² / r
=> 3 x 3 / 0.5
=> 18 m/s
Que-17: A boy is whirling 20 g stone in a horizontal circle by tying it to one end of a string of length 2.0 m. If the stone is making 4 revolutions in 1 second then, assuming the other end of the string stationary, calculate the tension produced in the string.
Ans- Tension = Force = mv²/r
=> m r ω²
=> 20 x 10^-3 x 2 x (2π x 4)²
=> 20 x 10^-3 x 2 x (2 x 3.14 x 4)²
=> 25.24 N
Que-18: A body of mass 1 kg tied to one end of a string is revolved at a rate of 3 rev/s in a circle of radius 10 cm. Calculate the linear velocity and acceleration of the body, and the tension in the string. What will happen if the string breaks?
Ans- v = r ω
=> v = 10 x 10^-2 x 2 π n
=> 10 x 10^-2 x 2 π x 3
=> 1.88 m/s
a = r ω²
=> 10 x 10^-2 (2π x 3)²
=> 35.5 m/s²
and F = m a
=> 1 x 35.5
=> 35.5 N
on the breaking of the string, tension (centripetal) would disappear and the body would leave the circle tangentially.
Que-19: A string can bear a maximum tension of 3.16 kg-wt. What maximum number of revolutions per second can be made by a stone of mass 49 g tied to one end of a 1 m long piece of this string so that the string may not break? (π = 22/7)
Ans- F = m r ω²
=>ω = √F/mr
=>2πn = √F/mr
=> n = 1/2π √F/mr
=> 1/(2 x 3.14) √(3.16 x 9.8) / (49 x 10^-3 x 1)
=> 4 N
—: end of Uniform Circular Motion Numerical on Angular Velocity Centripetal Acceleration and Force ISC Nootan Solutions :—
Return to : – Nootan Solutions for ISC Physics Class-11 Nageen Prakashan
Thanks
Please Share with your friends if helpful


