Arithmetic Quartiles Class 10 OP Malhotra Exe-18C ICSE Maths Solutions Ch-18

Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18C ICSE Maths Solutions Ch-18 Questions as latest prescribe guideline for upcoming exam. In this article you would learn How to Find Arithmetic Quartiles. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Arithmetic Quartiles Class 10 OP Malhotra Exe-18C ICSE Maths Solutions Ch-18

Board	ICSE
Publications	S Chand
Subject	Maths
Class	10th
Chapter-18	Arithmetic Mean, Median, Mode and Quartiles
Writer	OP Malhotra
Exe-18C	How to Find Arithmetic Quartiles
Edition	2024-2025

What is Arithmetic Quartiles

Just as Media divide distribution into two equal sub group, Quartile divide into four. Midian Quartile are the point of division. Hence second quartile is just same as median. When the set of observations are arranged in ascending order the quartiles are represented as,

First Quartile(Q1) = ((n + 1)/4)^t^h Term
Second Quartile(Q2) = ((n + 1)/2)^t^h Term
Third Quartile(Q3) = (3(n + 1)/4)^t^h Term

The 1^st quartile is also known as the lower quartile. 2^nd quartile is the same as the median dividing data into 2 equal parts. 3^rd quartile is also called the upper quartile.

The interquartile range is calculated as Upper Quartile – Lower Quartile.

Exercise- 18C (Arithmetic Quartiles)

Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18C ICSE Maths Solutions Ch-18

Que-1: Find Q₁, Q₃ for the following sets data :

(i) 38, 7, 43, 25, 20, 15, 12, 18, 11
(ii) 5, 12, 17, 23, 28, 31, 37, 41, 42, 49, 54, 58, 65, 68, 73, 77
(iii) 22, 21, 12, 15, 17, 18, 18, 20, 19, 1, 6, 25

Sol: (i) 38, 7, 43, 25, 20, 15, 12, 18, 11
Arranging in ascending order,
7, 11, 12. 15, 18, 20, 25, 38, 43
Here n = 9 which is odd
∴ Size of (n+1)/2 th term = (9+1)/2 = 2.5th term
Which lies in 12
Q1 = Size of 2nd term + 0.5 of (Size of 3rd term – 2nd term)
= 11 + 0.5 (12 – 11) = 11 + 0.5 × 1 = 11 + 0.5 = 11.5
Q3 = Size of {3(n+1)}/4 th term = {(9+1)/4}×3 = 30/4 = 7.5th term
= 7th term + 0.5 (8th term – 7th term)
= 25 + 0.5 (38 – 25) = 25 + (1/2) × 13 = 25 + 6.5 = 31.5

(ii) 5, 12. 17,23,28,31,37,41,42,49, 54, 58, 65, 68, 73, 77
There are 16 term which is even
(n+1)/4 = (16+1)/4 = 17/4 = 4.25th term
∴ Q1 = size of 4.25th term = 0
= Size of 4th term + 0.25 (28 – 23) = 23 + 0.25 × 5 = 23 + 1.25 = 24.25
Q3 = size of {(16+1)/4}×3 = 51/4th term = 12.75th term
= size of 12th term + 0.75 (13th term – 12th term) = 58 + 0.75 (65 – 58) = 58 + 0.75 × 7 = 58 + 5.25 = 63.25

(iii) 22, 21, 12, 15, 17. 18, 18. 20, 19. 1, 6. 25
Arranging in ascending order
1, 6, 12, 15, 17, 18, 18, 19, 20, 21, 22. 25
Here n = 12
∴ (n+1)/4 th term = (12+1)/4 = 13/4 = 3.25th term
Q1 = size of 3rd term + 0.25 (4th term – 3rd term)
= 12 + 0.25 (15 – 12) = 12 + 0.25 × 3 = 12 + 0.75 = 12.75
Now Q3 = {(n+1)/4} × 3 = {(12+1)4} × 3 = 39/4 = 9.75th term
Q3 = size of 9th term + 0.75 (10th term – 9th term)
= 20 + 0.75 (21 – 20) = 20 + 0.75 × 1 = 20 + 0.75 = 20.75

Que-2: In a class of ten students, the marks obtained by each student are shown against their Roll No’s given below:

Calculate the lower and the upper quartiles.

Sol: Arranging the marks obtain by the students in ascending order
2,4,8,10,12.15,20,25,30,40
Here n = 10
Lower Quartile (Q1) = (n+1)/4 = (10+1)/4 = 11/4 = 2.75th term
= 2nd term + 0.75 (3rd term – 2nd term) = 4 + 75 (8 – 4) = 4 + (75/4) × 4 = 4 + 3 = 7 marks
Upper Quartile (Q3) = {3(n+1)/4} = {11×3}/4 = 33/4 = 8.25th term
∴ Q3 = 8th term + .25 (9th term – 8th term)
= 25 + 0.25 (30 – 25)
= 25 + .25 × 5 = 25 + 1.25
= 26.25 marks

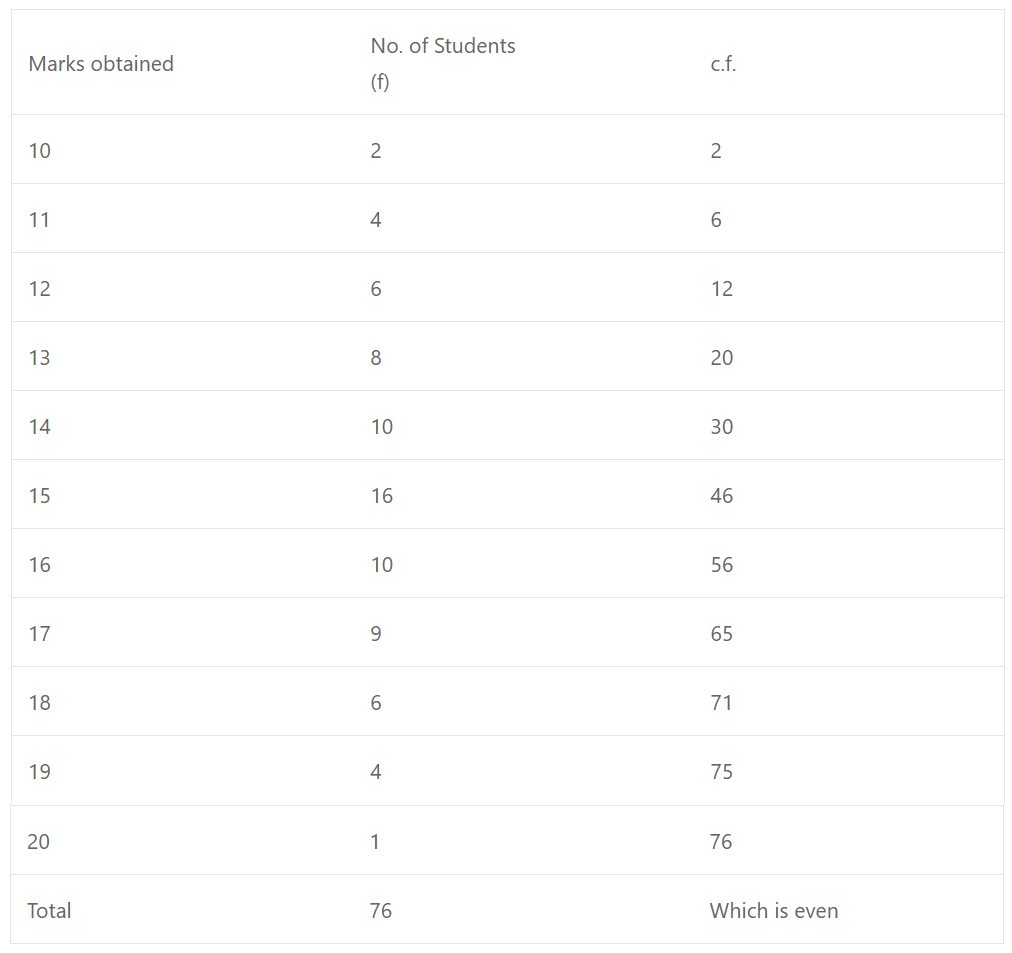
Que-3: From the data given below calculate the value of 3rd quartile.

Sol: Third Quartile (Q3) = 3n/4 = (3×76)/4 th = 57th term
Which is 17
∵ 57 lies between 57 – 65 in c.f.
∴ Q3 = 17 marks

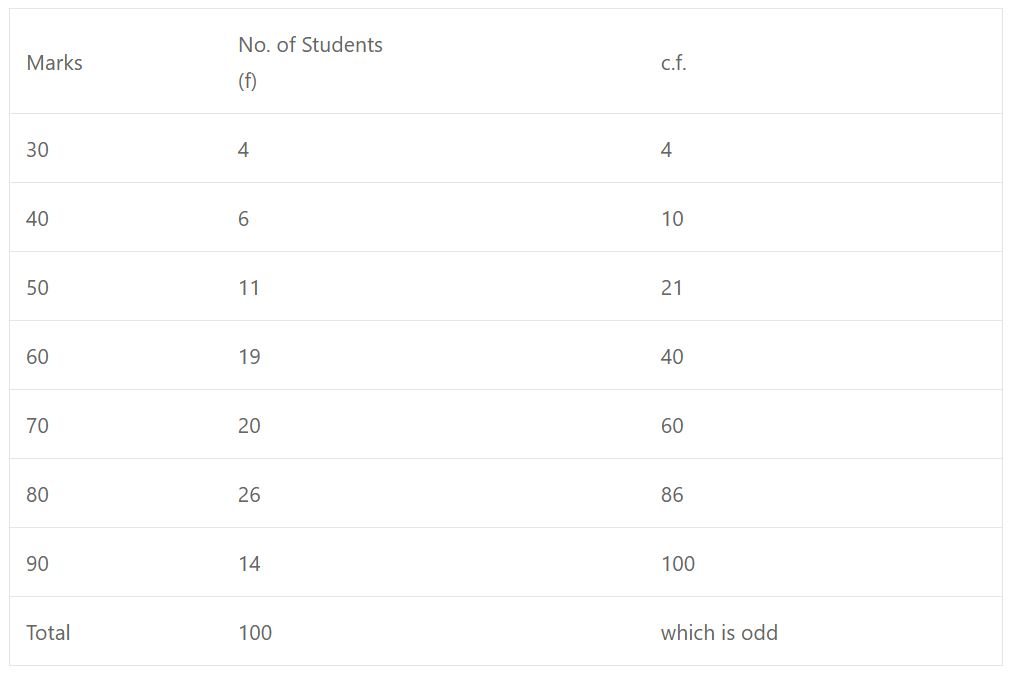
Que-4: Find both quartiles for the following distribution.

(i)

(ii)

Sol: (i) Here n = 100
∴ Q1 = (n+1)/4 = (100+1)/4th term = 101/4 = 25.25th term
which lies in 40 c.f.
∴ Q1 = 60
Q3 = {(n+1)/4} × 3 = {(100+1)/4} × 3 = (101×3)/4 th term = 303/4th = 75.75th term which lies in 86 c.f.
∴ Q3 = 80

(ii) Here n = 30
∴ Q1th term = (n+1)/4 = (30+1)/4th = 31/4th = 7.75th term
Which in 15 c.f.
∴ Q1 = 6
Q3th term = {(n+1)/4} × 3 = {(30+1)/4} × 3 = (31×3)/4 = 93/4 = 23.25th term which lies in 24th c.f.
∴ Q3 = 7

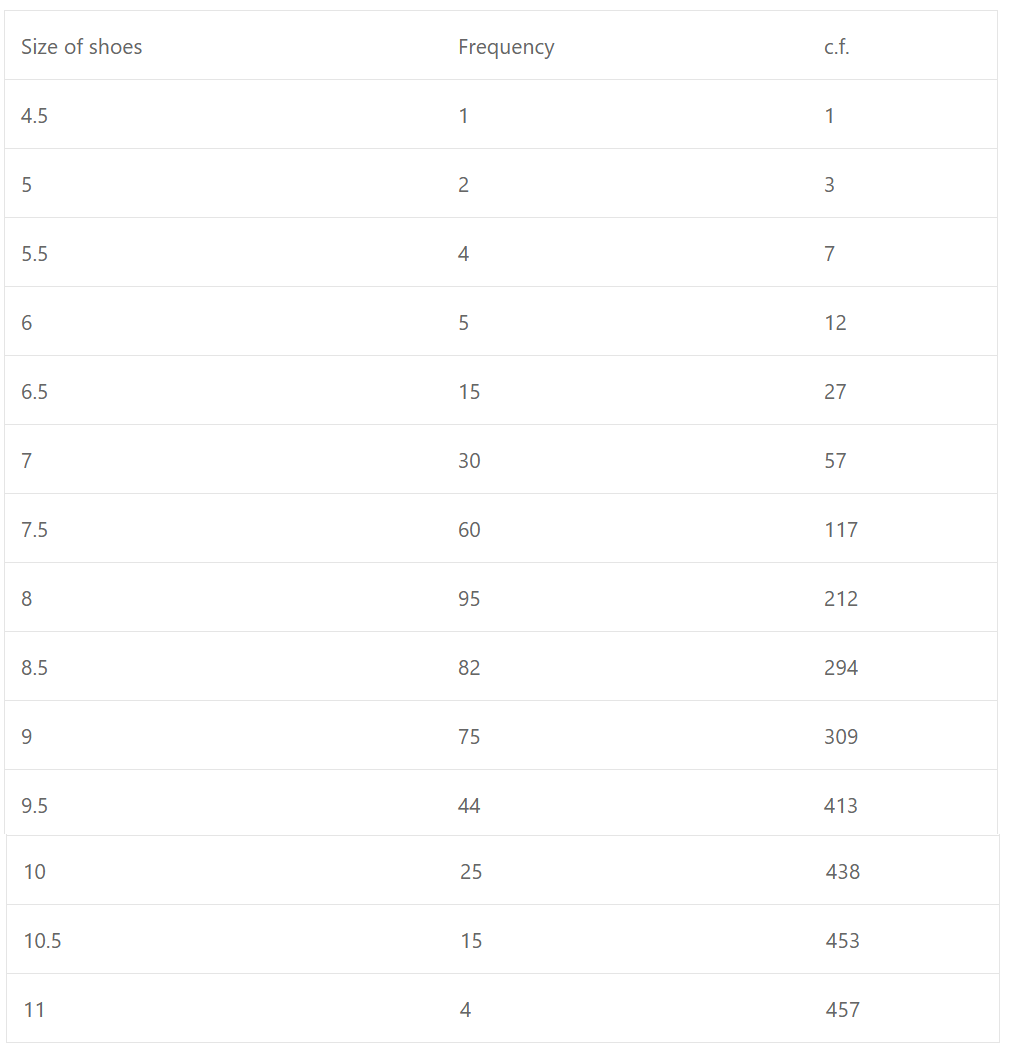
Que-5: Find the median size of the shoes from figures given below :

Also calculate the Quartiles.

Sol: Total 457 which is odd
∴ Median = (n+1)/2th = (457+1)/2th = 458/2 term = 229th term
Which lies between 213 – 294 in c.f.
∴ Median = 8.5
Q1 = (n+1)/2th = 458/4th = 114.5th term
Which lies between 58-117 in c.f.
∴ Q1 = 7.5
Q3 = {3(n+1)/4} th
= {3(457+1)}/4} th
= {3×458}/4 th
= 1374/4 th = 343.5th term
Which lies between 294 and 369
∴ Q3 = 9