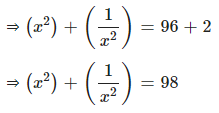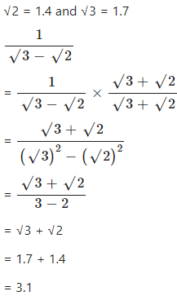Concise Rational and Irrational Numbers ICSE Class-9 Selina Solutions

Concise Rational and Irrational Numbers ICSE Class-9 Mathematics Selina Solutions Chapter-1 . We provide step by step Solutions of Exercise / lesson-1 Rational and Irrational Numbers for ICSE Class-9 Concise Selina Mathematics by RK Bansal. Our Solutions contain all type Questions with Exe-1 A, Exe-1 B and Exe-1 C , to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-9.

Concise Rational and Irrational Numbers ICSE Class-9 Mathematics Selina Solutions Chapter-1

–: Select Topics :–

Exe-1 A,

Exe-1 B,

Exe-1 C ,

Note:- Before viewing Solution of Chapter -1 Rational and Irrational Numbers Class-9 of Concise Selina Solutions. Read the Chapter Carefully then solve all example given in Exercise-1.1, Exercise-1.2, Exercise-1.3. For more practice on The Rational and Irrational Numbers Visit ML Aggarwal Rational and Irrational Numbers Chapter Also.

Exercise – 1(A) Rational and Irrational Numbers for ICSE Class-9 Maths Concise Selina Solutions

Question 1

Is zero a rational number ? Can it be written in the form $\frac{P}{q}$ , where p and q are integers and q≠0 ?

Answer

Yes, zero is a rational number.

As it can be written in the form of , where p and q are integers and q≠0 ?

⇒ 0 = $\frac{0}{1}$

Question 2

Are the following statement true or false ? Give reason for your answer.

Every whole number is a natural number.
Every whole number is a rational number.
Every integer is a rational number.
Every rational number is a whole number.

Answer

i) False, zero is a whole number but not a natural number.
ii) True, Every whole can be written in the formof, where p and q are integers and q≠0.
iii) True, Every integer can be written in the form of , where p and q are integers and q≠0.
iv) False.
Example : is a rational number, but not a whole number.

Question 3

Arrange $- \frac{5}{7}, \frac{7}{12}, - \frac{2}{3} and \frac{11}{18}$ in ascending order of their magnitudes.
Also, find the difference between the largest and smallest of these rational numbers. Express this difference as a decimal fraction correct to one decimal place.

Answer

Ans 3 Exercise - 1(A) Rational and Irrational Numbers ICSE Class-9th

Question 4

Arrange $\frac{5}{8}, - \frac{3}{16}, - \frac{1}{4} and \frac{17}{32}$ in descending order of their magnitudes.
Also, find the sum of the lowest and largest of these fractions. Express the result obtained as a decimal fraction correct to two decimal places.

Answer

Ans 4 Exercise - 1(A) Rational and Irrational Numbers ICSE Class-9th

Question 5.1

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : $\frac{7}{16}$

Answer

Given number is $\frac{7}{16}$

Since 16 = 2 x 2 x 2 x 2 = 2⁴ = 2⁴ x 5⁰
I.e. 16 can be expressed as 2^m x 5ⁿ

∴ $\frac{7}{16}$ is convertible into the terminating decimal.

Question 5.2

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : $\frac{23}{125}$

Answer

Given number is $\frac{23}{125}$

Since 125 = 5 x 5 x 5 = 5^{3 =}2⁰ x 5³
I.e. 125 can be expressed as 2^m x 5ⁿ

∴ $\frac{23}{125}$ is convertible into the terminating decimal.

Question 5.3

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : $\frac{9}{14}$

Answer

Given number is $\frac{9}{14}$

Since 14 = 2 x 7 = 2¹ x 7¹
I.e. 14 cannot be expressed as 2^m x 5ⁿ

∴ $\frac{9}{14}$ is not convertible into the terminating decimal.

Question 5.4

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : $\frac{32}{45}$

Answer

Given number is $\frac{32}{45}$

Since, 45 = 3 x 3 x 5 = 3² x 5¹
I.e. 45 cannot be expressed as 2^m x 5ⁿ

∴ $\frac{32}{45}$ is not convertible into the terminating decimal.

Question 5.5

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : $\frac{43}{50}$

Answer

Given number is $\frac{46}{50}$

Since 50 = 2 x 5 x 5 = 2¹ x 5²
I.e. 50 can be expressed as 2^m x 5ⁿ

∴ $\frac{43}{50}$ is convertible into the terminating decimal.

Question 5.6

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : $\frac{17}{40}$

Answer

Given number is $\frac{17}{40}$

Since 40 = 2 x 2 x 2 x 5 = 2³ x 5¹
I.e. 40 can be expressed as 2^m x 5ⁿ

∴ $\frac{17}{40}$ is convertible into the terminating decimal.

Question 5.7

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : $\frac{61}{75}$

Answer

Given number is $\frac{61}{75}$

Since 75 = 3 x 5 x 5 = 3¹ x 5²
i.e. 75 cannot be expressed as 2^m x 5ⁿ

∴ $\frac{61}{75}$ is not convertible into the terminating decimal.

Question 5.8

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : $\frac{123}{250}$

Answer

Given number is $\frac{123}{250}$

Since 250 = 2 x 5 x 5 x 5 = 2¹ x 5³
i.e. 250 can be expressed as 2^m x 5^n.1

∴ $\frac{123}{250}$ is convertible into the terminating decimal.

End of Exe-1 A Concise Rational and Irrational Numbers for ICSE Class-9

ICSE Class-9 Mathematics Concise Selina Solutions Exercise – 1(B) Rational and Irrational Numbers

Question 1.1

State, whether the following numbers is rational or not : ( 2 + √2 )²

Answer

( 2 + √2 )² = 2² + 2 ( 2 ) ( √2 ) + ( √2 )²
= 4 + 4√2 + 2
= 6 + 4√2

Irrational number.

Question 1.2

State, whether the following numbers is rational or not : ( 3 – √3 )²

Answer

( 3 – √3 )² = 3² + 2 ( 3 ) ( √3 ) + ( √3 )²
= 9 – 6√3 + 3
= 12 – 6√3 = 6 ( 2 – √3 )
Irrational number.

Question 1.3

State, whether the following numbers is rational or not : ( 5 + √5 )( 5 – √5 )

Answer

( 5 + √5 )( 5 – √5 ) = ( 5 )² – ( √5 )²
= 25 – 5 = 20
Rational Number

Question 1.4

State, whether the following numbers is rational or not : ( √3 – √2 )²

Answer

( √3 – √2 )² = ( √3 )² – 2 ( √3 )( √2 ) + ( √2 )²
= 3 – 2√6 + 2
= 5 – 2√6
Irrational Number

Question 1.5

State, whether the following numbers is rational or not :
${(\frac{3}{2 \sqrt{2}})}^{2}$

Answer

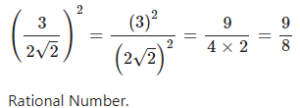
Question 1.6

State, whether the following number is rational or not :
${(\frac{\sqrt 7}{6 \sqrt{2}})}^{2}$

Answer

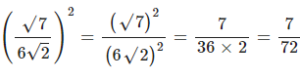
Question 2.1

Find the square of : $\frac{3 \sqrt{5}}{5}$

Answer

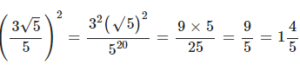
Question 2.2

Find the square of : √3 + √2

Answer

( √3 + √2 )² = ( √3 )² + 2( √3 )( √2 ) + ( √2 )²
= 3 + 2√6 + 2
= 5 + 2√6

Question 2.3

Find the square of : √5 – 2

Answer

( √5 – 2 )² = ( √5 )² – 2( √5 )( 2 ) + ( 2 )²
= 5 – 4√5 + 4
= 9 – 4√5

Question 2.4

Find the square of : 3 + 2√5

Answer

( 3 + 2√5 )² = 3² + 2( 3 )( 2√5) + ( 2√5 )²
= 9 + 12√5 + 20
= 29 + 12√5

Question 3.1

State, in each case, whether true or false :
√2 + √3 = √5

Options

True
False

Answer

False

Question 3.2

State, in each case, whether true or false :
2√4 + 2 = 6

Options

True
False

Answer

2√4 + 2 = 2 x 2 + 2 = 4 + 2 = 6 which is True.

Question 3.3

State, in each case, whether true or false :
3√7 – 2√7 = √7

Options

True
False

Answer

3√7 – 2√7 = √7 – True.

Question 3.4

State, in each case, whether true or false :
$\frac{2}{7}$ ia an irrational number.

Options

True
False

Answer

False Because $\frac{2}{7} = 0 . \bar{285714}$ which is recurring and non-terminating and hence it is rational.

Question 3.5

State, in each case, whether true or false :
$\frac{5}{11}$ is a rational number.

Options

True
False

Answer

True, because $\frac{5}{11} = 0 . \bar{45}$ which is recurring and non-terminating

Question 3.6

State, in each case, whether true or false :
All rational numbers are real numbers.

Options

True
False

Answer

True

Question 3.7

state, in each case, whether true or false :
All real numbers are rational numbers.

Options

True
False

Answer

False

Question 3.8

State, in each case, whether true or false :
Some real numbers are rational numbers.

Options

True
False

Answer

True

Question 4.1

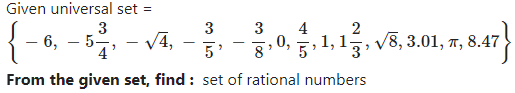
Answer

Given Universal set is

Question 4.2

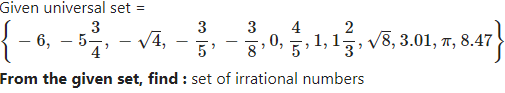
Answer

Question 4.3

Given universal set =
`{ -6, -5 3/4, -sqrt4, -3/5, -3/8, 0, 4/5, 1, 1 2/3, sqrt8, 3.01, π, 8.47 }`
From the given set, find : set of integers

Answer

Given Universal set is

`{ – 6, -5 3/4, -sqrt4, -3/5, -3/8, 0, 4/5, 1, 1 2/3, sqrt8, 3.01, π, 8.47 }`

We need to find the set of integers.
Set of integers consists of zero, the natural numbers and their additive inverses.
The set of integers is Z.
Z = `{ …… -3, -2, -1, 0, 1, 2, 3,……. }`
Here the set of integers is U ∩ Z = `{ -6, √4, 0, 1 }`

Question 4.4

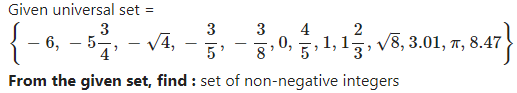
Answer

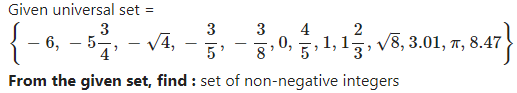
We need to find the set of non-negative integers.
Set of non-negative integers consists of zero and the natural numbers.
The set of non-negative integers is Z⁺ and Z⁺= { 0, 1, 2, 3,…… }
Here the set of integers is U ∩ Z⁺= {0, 1}

Question 5

Use method of contradiction to show that √3 and √5 are irrational numbers.

Answer

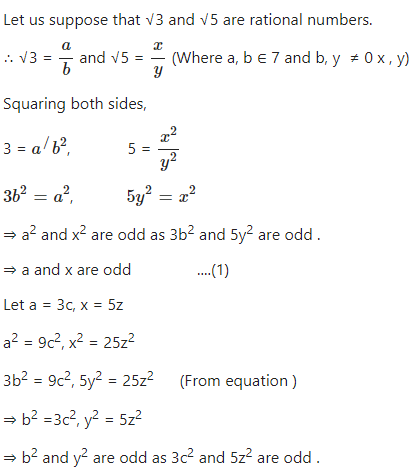
Question 6.1

Prove that the following number is irrational: √3 + √2

Answer

3 + √2
Let √3 + √2 be a rational number.
⇒ √3 + √2 = x
Squaring on both the sides, we get
( √3 + √2 )² = x²⇒ 3 + 2 + 2 x √3 x √2 = x²

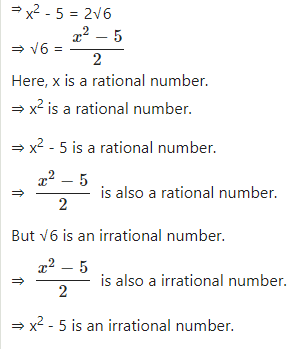
⇒ x² is an irrational number.

⇒ x is an irrational number.

But we have assume that x is a rational number.

∴ we arrive at a contradiction.

So, our assumption that √3 + √2 is a rational number is wrong.

∴ √3 + √2 is an irrational number.

Question 6.2

Prove that the following number is irrational: 3 – √2

Answer

3 – √2
Let 3 – √2 be a rational number.
⇒ 3 – √2 = x
Squaring on both the sides, we get
( 3 – √2 )² = x²⇒ 9 + 2 – 2 x 3 x √2 = x²
^⇒ 11 – x² = 6√2

⇒ 11 – x² is an irrational number.

⇒ x² is an irrational number.

⇒ x is an irrational number.

But we have assume that x is a rational number.

∴ we arrive at a contradiction.

So, our assumption that 3 – √2 is a rational number is wrong.
∴ 3 – √2 is an irrational number.

Question 6.3

Prove that the following number is irrational: √5 – 2

Answer

√5 – 2
Let √5 – 2 be a rational number.
⇒ √5 – 2 = x
Squaring on both the sides, we get
${(\sqrt 5 - 2)}^{2} = x^{2}$

⇒ 5 + 4 – 2 x 2 x √5 = x²

⇒ 9 – x²= 4√5

⇒ √5 = $\frac{9 - x^{2}}{4}$

Here, x is a rational number.

⇒ 9 – x² is an irrational number.

⇒ x² is an irrational number.

⇒ x is an irrational number.

But we have assume that x is a rational number.

∴ we arrive at a contradiction.

So, our assumption that √5 – 2 is a rational number is wrong.
∴ √5 – 2 is an irrational number.

Question 7

Write a pair of irrational numbers whose sum is irrational.

Answer

√3 + 5 and √5 – 3 are irrational numbers whose sum is irrational.
( √3 + 5 ) + ( √5 – 3 ) = √3 + √5 + 5 – 3 = √3 + √5 + 2 which is irrational.

Question 8

Write a pair of irrational numbers whose sum is rational.

Answer

√3 + 5 and 4 – √3 are two irrational numbers whose sum is rational.
( √3 + 5 ) + ( 4 – √3 ) = √3 + 5+ 4 – √3 = 9

Question 9

Write a pair of irrational numbers whose difference is irrational.

Answer

√3 + 2 and √2 – 3 are two irrational numbers whose difference is irrational.
( √3 + 2 ) – ( √2 – 3 ) = √3 – √2 + 2 + 3 = √3 – √2 + 5 which is irrational.

Question 10

Write a pair of irrational numbers whose difference is rational.

Answer

√5 – 3 and √5 + 3 are irrational numbers whose difference is rational.
( √5 – 3 ) – ( √5 + 3 ) = √5 – 3 – √5 – 3 = -6 which is rational.

Question 11

Write a pair of irrational numbers whose product is irrational.

Answer

Consider two irrational numbers ( 5 + √2 ) and ( √5 – 2 )
Thus, the product, ( 5 + √2 ) x ( √5 – 2 ) = 5√5 – 10 + √10 – 2√2 is irrational.

Question 12

Write a pair of irrational numbers whose product is rational.

Answer

Consider √2 as an irrational number.
√2×√2= √4= 2 which is a rational number.

Question 13.1

Write in ascending order: 3√5 and 4√3

Answer

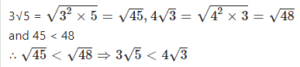
Question 13.2

Write in ascending order : $2 \sqrt[3]{5} and 3 \sqrt[3]{2}$

Answer

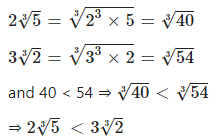
Question 13.3

Write in ascending order : 6√5, 7√3, and 8√2

Answer

6√5 = $\sqrt{6^{2} \times 5} = \sqrt{180}$

7√3 = $\sqrt{7^{2} \times 3} = \sqrt{147}$

8√2 = $\sqrt{8^{2} \times 2} = \sqrt{128}$

and 128 < 147 < 180

∴ √128 < √147 < √180

⇒ 8√2 < 7√3 < 6√5

Question 13.4

Write in ascending order : 6√5, 7√3 and 8√2

Answer

$6 \sqrt{5} = \sqrt{6^{2} \times 5} = \sqrt{180}$

$7 \sqrt{3} = \sqrt{7^{2} \times 3} = \sqrt{147}$

$8 \sqrt{2} = \sqrt{8^{2} \times 2} = \sqrt{128}$

and 128 < 147 < 180

∴ $\sqrt{128} < \sqrt{147} < \sqrt{180}$

⇒ $8 \sqrt{2} < 7 \sqrt{3} < 6 \sqrt{5}$

Question 14.1

Write in descending order: $2 \sqrt[3]{6} and 3 \sqrt[4]{2}$

Answer

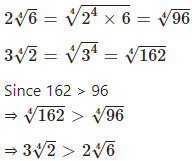
Ans 14.1 Exercise - 1(B) Rational and Irrational Numbers ICSE Class-9th

Question 14.2

Write in descending order: 7√3 and 3√7

Answer

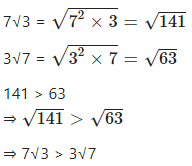
Question 15.1

Answer

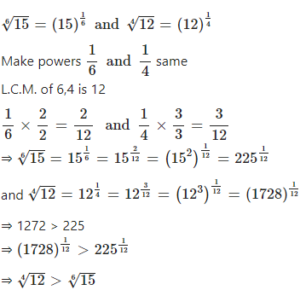
Question 15.2

Compare : $\sqrt{24} and \sqrt[3]{35}$

Answer

Question 16.

Insert two irrational numbers between 5 and 6.

Answer

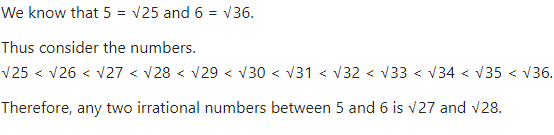
Question 17.

Insert five irrational numbers between 2√5 and 3√3.

Answer

We know that 2√5 = $\sqrt{4 \times 5}$ = √20 and 3√3 = √20

Thus, We have, √20 < √21 < √22 < √23 < √24 < √25 < √26 < √27.
So any five irrational numbers between 2√5 and 3√3 are :
√21, √22, √23, √24, and √26.

Question 18.

Write two rational numbers between √2 and √3.

Answer

Question 19.

Write three rational numbers between √3 and √5.

Answer

Question 20.1

Answer

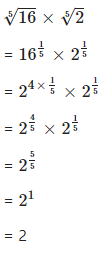
Question 20.2

Answer

Question 20.3

Simplify : ( 3 + √2 )( 4 + √7 )

Answer

( 3 + √2 )( 4 + √7 )
= 3 x 4 + 3 x √7 + 4 x √2 + √2 x √7
= 12 + 3√7 + 4√2 + √14

Question 20.4

Simplify : (√3 – √2 )²

Answer

(√3 – √2 )²

= ( √3 )² + ( √2 )² – 2 x √3 x √2

= 3 + 2 – 2√6

= 5 – 2√6

End of Exe-1 B Concise Rational and Irrational Numbers for ICSE Class-9

Selina Solutions of Exercise – 1(C) Rational and Irrational Numbers Concise Maths for ICSE Class-9

Question 1.1

State, with reason, of the following is surd or not : √180

Answer

√180 = $\sqrt{2 \times 2 \times 5 \times 3 \times 3}$ = 6√5 which is irrational.
∴ √180 is a surds.

Question 1.2

State, with reason, of the following is surd or not :
$\sqrt[4]{27}$

Answer

Ans 1.2 Exercise - 1(C) Rational and Irrational Numbers ICSE Class-9th

Question 1.3

Answer

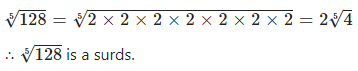
Answer 1.3 Exercise - 1(C) Rational and Irrational Numbers ICSE Class-9th

Question 1.4

Question 1.4 Exercise - 1(C) Rational and Irrational Numbers ICSE Class-9th

Answer

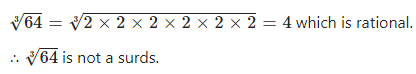
Ans 1.4 Exercise - 1(C) Rational and Irrational Numbers ICSE Class-9th

Question 1.5

State, with reason, of the following is surd or not :
$\sqrt[3]{25} . \sqrt[3]{40}$

Answer

Question 1.6

State, with reason, of the following is surd or not :
…..

Answer

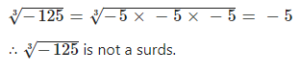
Question 1.7

State, with reason, of the following is surd or not : √π

Answer

√π not a surds as π is irrational.

Question 1.8

State, with reason, of the following is surd or not :
$\sqrt{3 + \sqrt{2}}$

Answer

$\sqrt{3 + \sqrt{2}}$ is not a surds because 3 + √2 is irrational.

Question 2.1

Write the lowest rationalising factor of : 5√2

Answer

5√2 x 5√2 = 5 x 2 = 10 which is rational.

∴ lowest rationalizing factor is √2

Question 2.2.

Write the lowest rationalising factor of : √24

Answer

Question 2.3

Write the lowest rationalising factor of : √5 – 3

Answer

( √5 – 3 )( √5 + 3 ) = ( √5 )² – (3)² = 5 – 9 = -4

∴ lowest rationalizing factor is ( √5 + 3 )

Question 2.4

Write the lowest rationalising factor of : 7 – √7

Answer

7 – √7
( 7 – √7 )( 7 + √7 ) = 49 – 7 = 42
Therefore, lowest rationalizing factor is ( 7 + √7 ).

Question 2.5

Write the lowest rationalising factor of : √18 – √50

Answer

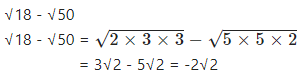
∴ lowest rationalizing factor is √2

Question 2.6

Write the lowest rationalising factor of : √5 – √2

Answer

√5 – √2
( √5 – √2 )( √5 + √2 ) = ( √5 )² – ( √2 )² = 3

Therefore lowest rationalizing factor is √5 + √2

Question 2.7

Write the lowest rationalising factor of : √13 + 3

Answer

( √13 + 3 )( √13 – 3 ) = ( √13 )² – 3² = 13 – 9 = 4

Its lowest rationalizing factor is √13 – 3.

Question 2.8

Write the lowest rationalising factor of : 15 – 3√2

Answer

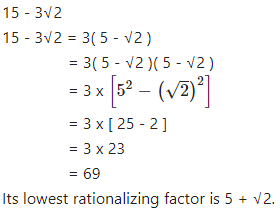
Question 2.9

Write the lowest rationalising factor of : 3√2 + 2√3

Answer

3√2 + 2√3
= ( 3√2 + 2√3 )( 3√2 – 2√3 )
= ( 3√2)² – (2√3)²
= 9 x 2 – 4 x 3
= 18 – 12
= 6
its lowest rationalizing factor is 3√2 – 2√3.

Question 3.1

Rationalise the denominators of : $\frac{3}{\sqrt{5}}$

Answer

3√5×√5√5=3√5/5

Question 3.2

Rationalise the denominators of : $\frac{2 \sqrt{3}}{\sqrt{5}}$

Answer

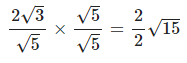
Question 3.3

Rationalise the denominators of : $\frac{1}{\sqrt{3} - \sqrt{2}}$

Answer

Question 3.4

Rationalise the denominators of :

Answer

Question 3.5

Rationalise the denominators of : $\frac{2 - \sqrt 3}{2 + \sqrt 3}$

Answer

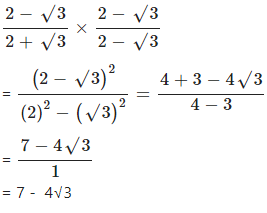
Question 3.6

Rationalise the denominators of : $\frac{\sqrt{3} + 1}{\sqrt{3} - 1}$

Answer

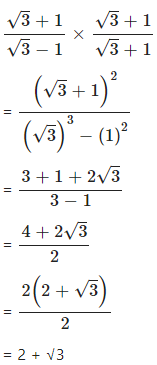
Question 3.7

Rationalise the denominators of : $\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}}$

Answer

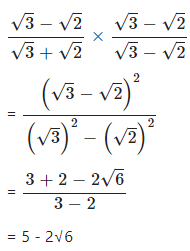
Question 3.8

Rationalise the denominators of : $\frac{\sqrt{6} - \sqrt{5}}{\sqrt{6} + \sqrt{5}}$

Answer

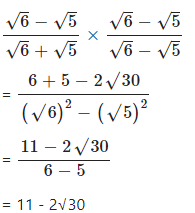
Question 3.9

Rationalise the denominators of : …………………

Answer

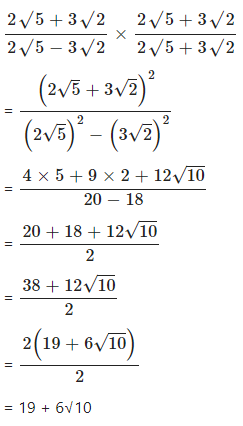
Question 4.1

Find the values of ‘a’ and ‘b’ in each of the following :
………

Answer

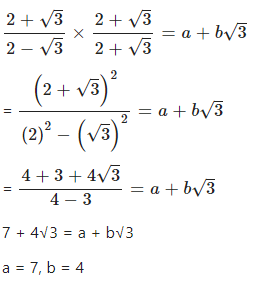
Question 4.2

Find the values of ‘a’ and ‘b’ in each of the following:….. $\frac{\sqrt{7} - 2}{\sqrt{7} + 2} = a \sqrt{7} + b$

Answer

Question 4.3

Find the values of ‘a’ and ‘b’ in each of the following:
$\frac{3}{\sqrt{3} - \sqrt{2}} = a \sqrt{3} - b \sqrt{2}$

Answer

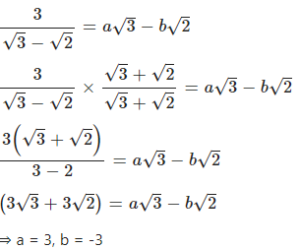
Question 4.4

Find the values of ‘a’ and ‘b’ in each of the following

Answer

Question 5.1

Simplify :
$\frac{22}{2 \sqrt{3} + 1} + \frac{17}{2 \sqrt{3} - 1}$

Answer

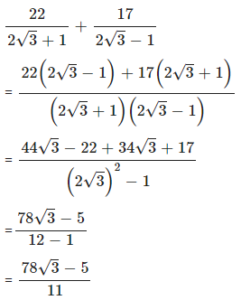
Question 5.2

Simplify :
…………….

Answer

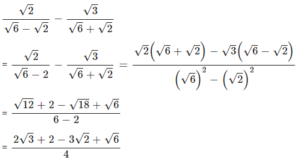
Question 6.1

f x =…………………………find

Answer

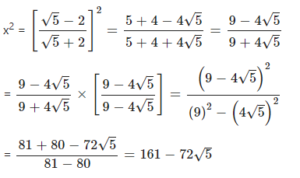
Question 6.2

f x =…………………; find : y²

Answer

Question 6.3

If x =…………………; find : xy

Answer

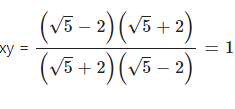
Question 6.4

If x =………………….; find :
x² + y² + xy.

Answer

x² + y² + xy
= 161 – 72√5 + 161 +72√5 + 1

= 322 + 1 = 323

Question 7.1

If m = ………… find m²

Answer

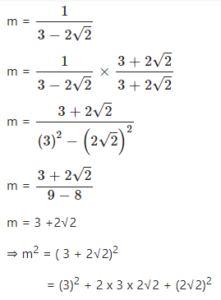
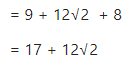
Question 7.2

If m = ……………….. $\frac{1}{3 - 2 \sqrt{2}} and n = \frac{1}{3 + 2 \sqrt{2}},$ find n²

Answer

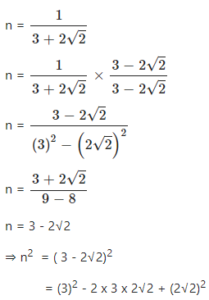
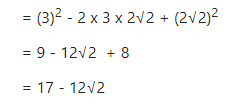
Question 8.1

If x = 2√3 + 2√2 , find : …..

Answer

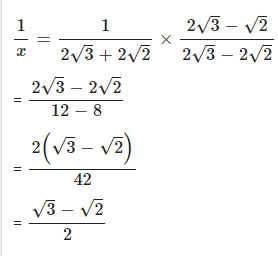
Question 8.2

If x = 2√3 + 2√2 , find : ……..

Answer

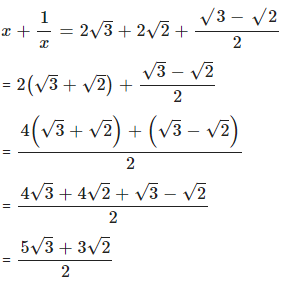
Question 8.3

If x = 2√3 + 2√2 , find :…..

Answer

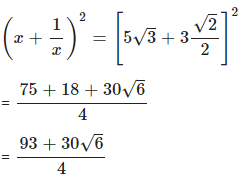
Question 9

If x = 1 – √2, find the value of ……

Answer

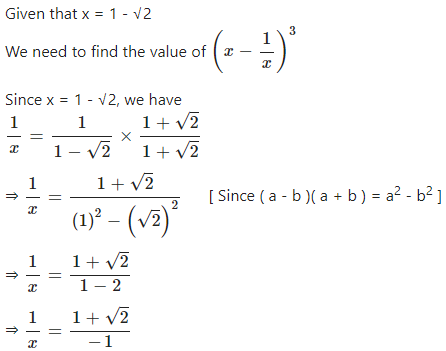
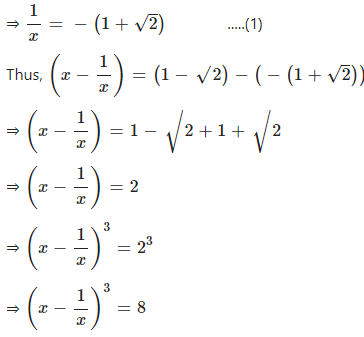
Question 10

If x = 5 – 2√6, find $x^{2} + \frac{1}{x^{2}}$

Answer

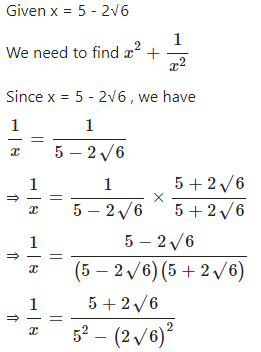
Question 11

Show that : ……………..

Answer

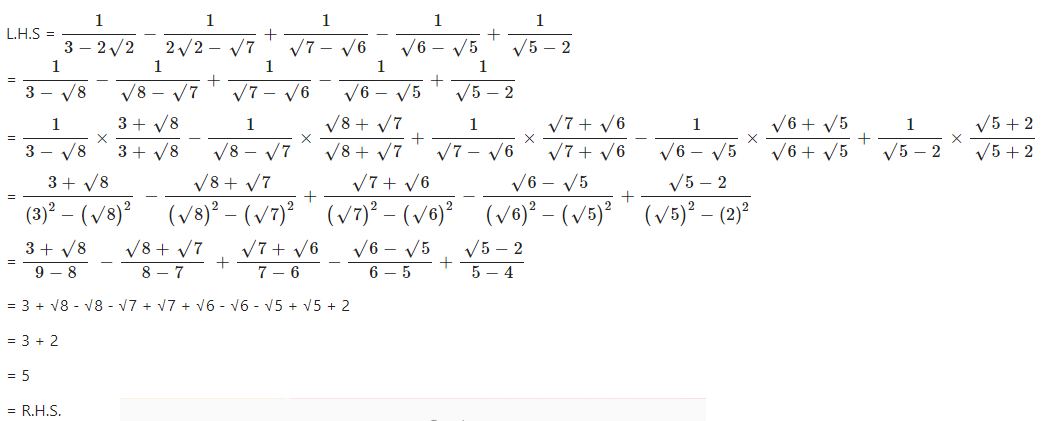
Question 12

Rationalise the denominator of : $\frac{1}{\sqrt 3 - \sqrt 2 + 1}$

Answer

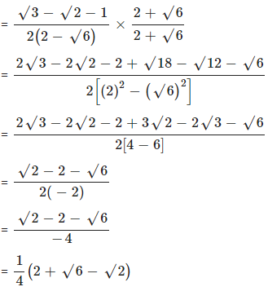
Question 13.1

If √2 = 1.4 and √3 = 1.7, find the value of :…………..

Answer

Question 13.2

If √2 = 1.4 and √3 = 1.7, find the value of : ………

Answer

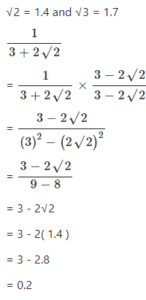
Question 13.3

Simplify : $\frac{2 - \sqrt 3}{\sqrt 3}$

Answer

Question 14

Evaluate : $\frac{4 - \sqrt 5}{4 + \sqrt 5} + \frac{4 + \sqrt 5}{4 - \sqrt 5}$

Answer

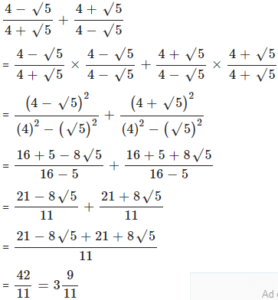
Question 15

If $\frac{2 + \sqrt 5}{2 - \sqrt 5} = x and \frac{2 - \sqrt 5}{2 + \sqrt 5} = y$ ; find the value of x² – y².

Answer

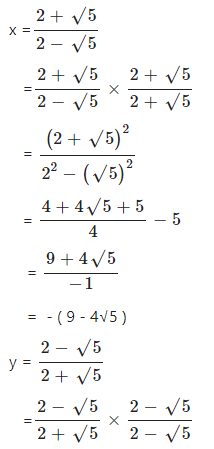
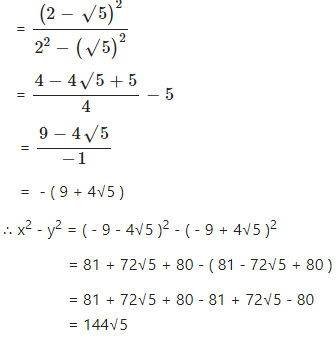
Question 16

Simplify : $\frac{\sqrt{18}}{5 \sqrt{18} + 3 \sqrt{72} - 2 \sqrt{162}}$

Answer

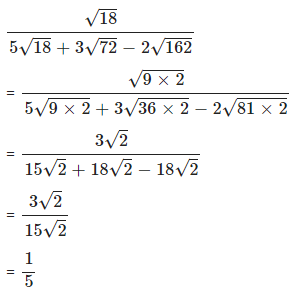
— End of Exe-1 C Concise Rational and Irrational Numbers Solutions :–

Return to – Concise Selina Maths Solutions for ICSE Class -9

Thanks

Share with your friends

Loci Class 10 OP Malhotra Exe-13B ICSE Maths Solutions

The Night Mail Line by Line Explanation: ICSE Class 10 English Poem

The Night Mail Summary: Treasure Chest English for ICSE Class 9