Concise Solution Linear In Equations in One Variable Chapter 4 ICSE Class 10

Note:- Before viewing Solution of Chapter-4 Linear Equations in One Variable of Concise Solution read the Chapter Carefully then solve all example of your text book. The Chapter Chapter-4 Linear Equations in One Variable is important Chapter in ICSE board.

Exercise 4-(A) of  Concise Solution Linear in Equations in One Variable Chapter 4 

Question 1

State, true or false:

Answer 1

Question 2

State, whether the following statements are true or false:

(i) a < b,  then a – c < b – c

(ii) If a > b, then a + c > b + c

(iii) If a < b, then ac > bc

(iv) If a > b, then 

(v) If a – c > b – d, then a + d > b + c

(vi) If a < b, and c > 0, then a – c > b – c

Where a, b, c and d are real numbers and c0.

Answer 2

(i) a < ba – c < b – c

The given statement is true.

(ii) If a > ba + c > b + c

The given statement is true.

(iii) If a < b  ac < bc

The given statement is false.

(iv) If a > b 

The given statement is false.

(v) If a – c > b – d     a + d > b + c

The given statement is true.

(vi) If a < b  a – c < b – c (Since, c > 0)

The given statement is false.

Question 3

If x  N, find the solution set of inequations.

(i) 5x + 32x + 18

(ii) 3x – 2 < 19 – 4x

Answer 3

(i) 5x + 3  2x + 18

5x – 2x 18 – 3

3x   15

x   5

Since, x  N, therefore solution set is {1, 2, 3, 4, 5}.

(ii) 3x – 2 < 19 – 4x

3x + 4x < 19 + 2

7x < 21

x < 3

Since, x  N, therefore solution set is {1, 2}.

Question 4

If the replacement set is the set of whole numbers, solve:

(i) x + 7 11

(ii) 3x – 1 > 8

(iii) 8 – x > 5

(iv) 7 – 3x

(v)

(vi) 18  3x – 2

Answer 4

(i) x + 7   11

x 11 – 7

x  4

Since, the replacement set = W (set of whole numbers)

Solution set = {0, 1, 2, 3, 4}

(ii) 3x – 1 > 8

3x > 8 + 1

x > 3

Since, the replacement set = W (set of whole numbers)

Solution set = {4, 5, 6, …}

(iii) 8 – x > 5

– x > 5 – 8

– x > -3

x < 3

Since, the replacement set = W (set of whole numbers)

Solution set = {0, 1, 2}

(iv) 7 – 3x 

-3x  -7

-3x

x 

Since, the replacement set = W (set of whole numbers)

Solution set = {0, 1, 2}

(v)

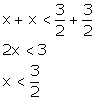
Since, the replacement set = W (set of whole numbers)

Solution set = {0, 1}

(vi) 18  3x – 2

18 + 2   3x

20  3x

Since, the replacement set = W (set of whole numbers)

Solution set = {7, 8, 9, …}

Question 5

Solve the inequation:

3 – 2x     x – 12 given that x    N.

Answer 5

3 – 2x x – 12

-2x – x  -12 – 3

-3x -15

x5

Since, x  N, therefore,

Solution set = {1, 2, 3, 4, 5}

Question 6

If 25 – 4x  16, find:

(i) the smallest value of x, when x is a real number,

(ii) the smallest value of x, when x is an integer.

Answer 6

25 – 4x  16

-4x  16 – 25

-4x  -9

x

x

(i) The smallest value of x, when x is a real number, is 2.25.

(ii) The smallest value of x, when x is an integer, is 3.

Question 7

If the replacement set is the set of real numbers, solve:

Answer 7

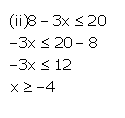
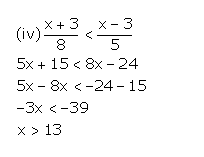
Question 8

Find the smallest value of x for which 5 – 2x <      , where x is an integer.

Answer 8

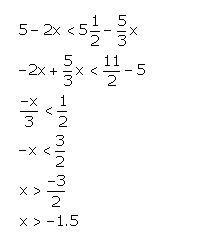
Question 9

Find the largest value of x for which

2(x – 1) ≤ 9 – x and x  W.

Answer 9

2(x – 1) ≤9 – x

2x – 2 ≤  9 – x

2x + x  ≤ 9 + 2

3x  ≤11

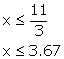
Since, x  W, thus the required largest value of x is 3.

Question 10

Solve the in equation:   and x   R.

Answer 10

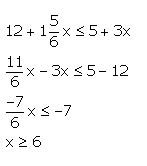
Question 11

Given x {integers}, find the solution set of:

Answer 11

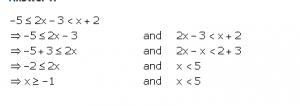
Question 12

Given x  {whole numbers}, find the solution set of:

.

Answer 12

Chapter 4 – Linear in Equations in One Variable Exercise-4(B) Concise Selina Solution

Question 1

Represent the following inequalities on real number lines:

Answer 1

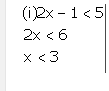
Solution on number line is:

Question 2

For each graph given, write an in equation taking x as the variable:

Answer 2

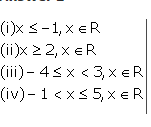
Question 3

For the following in equations, graph the solution set on the real number line:

Question 4

Represent the solution of each of the following inequalities on the real number line:

The solution on number line is:

Question 5

x  € {real numbers} and -1 < 3 – 2x 7, evaluate x and represent it on a number line.

Answer 5

-1 < 3 – 2x  7

-1 < 3 – 2x and 3 – 2x  7

2x < 4 and -2x  4

x < 2 and x  -2

Solution set = {-2  x < 2, x  R}

Thus, the solution can be represented on a number line as:

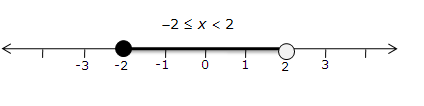
Question 6

List the elements of the solution set of the in equation

-3 < x – 2 ≤ 9 – 2x; x  N.

Answer 6

-3 < x – 2  ≤ 9 – 2x

-3 < x – 2 and x – 2 ≤ 9 – 2x

-1 < x and 3x  ≤ 11

-1 < x

Since, x  N

Solution set = {1, 2, 3}

Question 7

Find the range of values of x which satisfies

Graph these values of x on the number line.

Answer 7

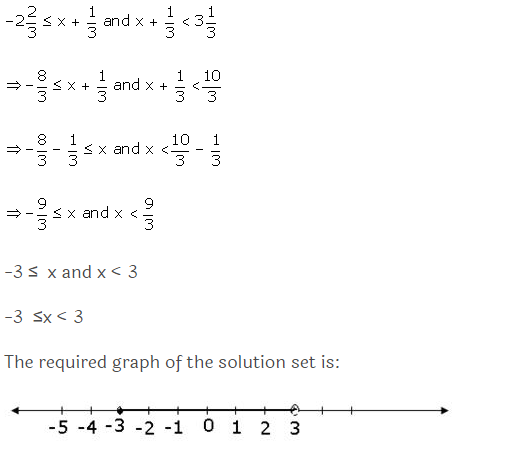
Question 8

Find the values of x, which satisfy the in equation:

Graph the solution on the number line.

Answer 8

Question 9

Given x  {real numbers}, find the range of values of x for which -5  ≤2x – 3 < x + 2 and represent it on a number line.

Answer 9

-5  ≤ 2x – 3 < x + 2

-5 ≤ 2x – 3 and 2x – 3 < x + 2

-2 ≤  2x and x < 5

-1 ≤ x and x < 5≤

Required range is -1 ≤ x < 5.

The required graph is:

Question 10

If 5x – 3 ≤ 5 + 3x  ≤ 4x + 2, express it as a ≤ x ≤ b and then state the values of a and b.

Answer 10

5x – 3 ≤ 5 + 3x ≤ 4x + 2

5x – 3 ≤ 5 + 3x and 5 + 3x ≤ 4x + 2

2x  ≤ 8 and -x   -3

x ≤ 4 and x ≤ 3

Thus, 3 ≤ x ≤4.

Hence, a = 3 and b = 4.

Question 11

Solve the following in equation and graph the solution set on the number line:

2x – 3 < x + 2  ≤ 3x + 5, x  € R.

Answer 11

2x – 3 < x + 2 ≤ 3x + 5

2x – 3 < x + 2 and x + 2 ≤ 3x + 5

x < 5 and -3 ≤ 2x

x < 5 and -1.5 ≤  x

Solution set = {-1.5 ≤ x < 5}

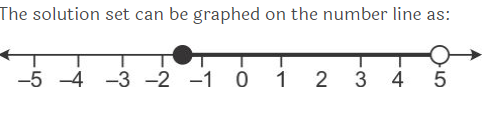
Question 12

Solve and graph the solution set of:

(i) 2x – 9 < 7 and 3x + 9 ≤ 25, x € R

(ii) 2x – 9 ≤ 7 and 3x + 9 > 25, x € I

(iii) x + 5  4(x – 1) and 3 – 2x < -7, x  R

Answer 12

(i) 2x – 9 < 7 and 3x + 9  25

2x < 16 and 3x  16

x < 8 and x 5

Solution set = { x  5, x  R}

The required graph on number line is:

(ii) 2x – 9  7 and 3x + 9 > 25

2x  16 and 3x > 16

x  8 and x > 5

Solution set = {5 < x  8, x  I} = {6, 7, 8}

The required graph on number line is:

(iii) x + 5  4(x – 1) and 3 – 2x < -7

9  3x and -2x < -10

3  x and x > 5

Solution set = Empty set

Question 13

Solve and graph the solution set of:

(i) 3x – 2 > 19 or 3 – 2x ≥ -7, x € R

(ii) 5 > p – 1 > 2 or 7 ≤ 2p – 1  17, p € R

Answer 13

(i) 3x – 2 > 19 or 3 – 2x ≥ -7

3x > 21 or -2x ≥ -10

x > 7 or x ≤ 5

Graph of solution set of x > 7 or x  5 = Graph of points which belong to x > 7 or x ≤ 5 or both.

Thus, the graph of the solution set is:

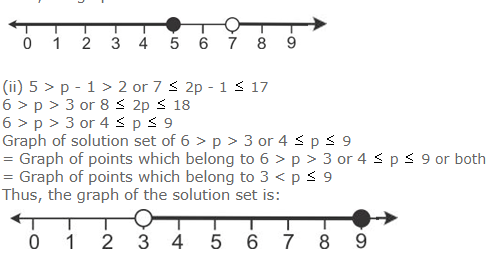
Question 14

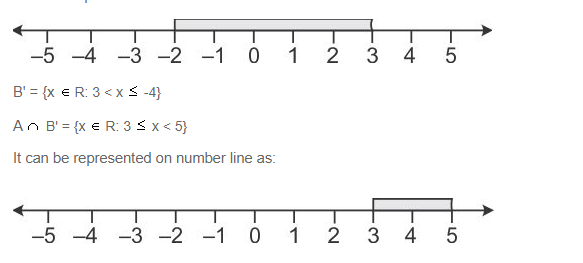
The diagram represents two in equations A and B on real number lines:

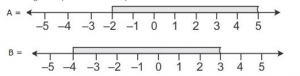
(i) Write down A and B in set builder notation.

(ii) Represent A  B and A  B’ on two different number lines.

Answer 14

(i) A = {x  R: -2 x < 5}

B = {x  R: -4 x < 3}

(ii) A  B = {x  R: -2  x < 5}

It can be represented on number line as:

Question 15

Use real number line to find the range of values of x for which:

(i) x > 3 and 0 < x < 6

(ii) x < 0 and -3  x < 1

(iii) -1 < x  6 and -2  x  3

Answer 15

Question 16

Illustrate the set {x: -3  x < 0 or x > 2, x  R} on the real number line.

Answer 16

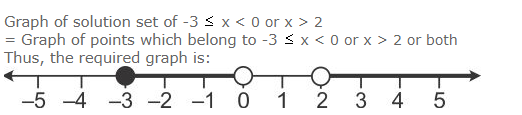
Question 17

Given A = {x: -1 < x ≤ 5, x  ≤R} and B = {x: -4  x < 3, x ≤ R}

Represent on different number lines:

(i) A ∩ B

(ii) A’ ∩ B

(iii) A – B

Answer  17

Question 18

P is the solution set of 7x – 2 > 4x + 1 and Q is the solution set of 9x – 45  5(x – 5); where x  R. Represent:

(i) P Q

(ii) P – Q

(iii) PQ’

on different number lines.

Answer 18

Question 19

Find the range of values of x, which satisfy:

Graph, in each of the following cases, the values of x on the different real number lines:

(i) x  W (ii) x  Z (iii) x  R

Answer 19

Question 20

Given: A = {x: -8 < 5x + 2 ≤ 17, x € I}, B = {x: -2 ≤ 7 + 3x < 17, x € R}

Where R = {real numbers} and I = {integers}. Represent A and B on two different number lines. Write down the elements of A ∩ B.

Answer 20

A = {x: -8 < 5x + 2 ≤ 17, x€  I}

= {x: -10 < 5x ≤ 15, x € I}

= {x: -2 < x ≤ 3, x € I}

It can be represented on number line as follows:

B = {x: -2 ≤ 7 + 3x < 17, x € R}

= {x: -9 ≤ 3x < 10, x € R}

= {x: -3 ≤ x < 3.33, x € R}

It can be represented on number line as follows:

A  B = {-1, 0, 1, 2, 3}

Question 21

Solve the following inequation and represent the solution set on the number line 2x – 5 ≤ 5x +4 < 11, where x  I

Answer 21

2x – 5 ≤ 5x +4 and 5x +4 < 11

2x – 5x ≤ 4 – 5 and 5x < 11 – 4

3x ≤ – 1 and 5x < 7

x ≥ – 1 and x <

x ≥ – 1 and x <

Since x I, the solution set is

And the number line representation is

Question 22

Given that x € I, solve the in equation and graph the solution on the number line:

Answer 22

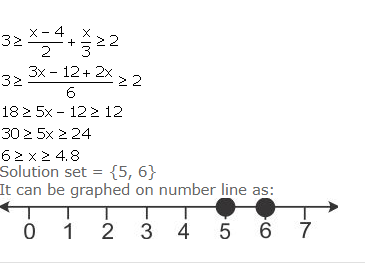
Question 23

Given:

A = {x: 11x – 5 > 7x + 3, x € R} and

B = {x: 18x – 9  15 + 12x, x € R}.

Find the range of set A ∩ B and represent it on number line.

Answer 23

Question 24

Find the set of values of x, satisfying:

7x + 3 ≥ 3x – 5 and   , where x  N.

Answer 24

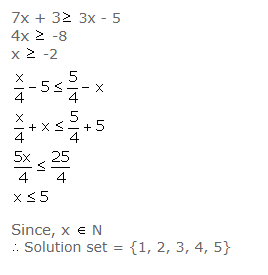
Question 25

Solve:

(i)    , where x is a positive odd integer.

(ii)     , where x is a positive even integer.

Answer 25

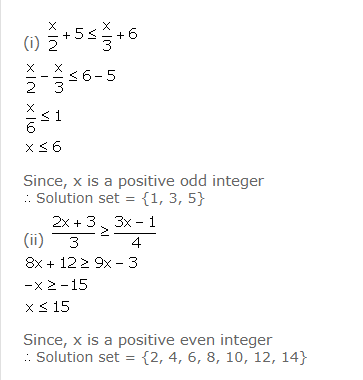
Question 26

Solve the inequation:

  , x W. Graph the solution set on the number line.

Answer 26

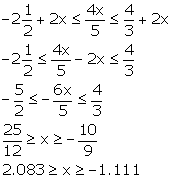
Since, x € W

Solution set = {0, 1, 2}

The solution set can be represented on number line as:

Question 27

Find three consecutive largest positive integers such that the sum of one-third of first, one-fourth of second and one-fifth of third is at most 20.

Answer 27

Let the required integers be x, x + 1 and x + 2.

According to the given statement,

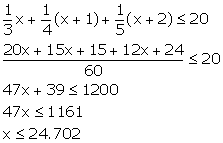
Thus, the largest value of the positive integer x is 24.

Hence, the required integers are 24, 25 and 26.

Question 28

Solve the given in equation and graph the solution on the number line.

Answer 28

2y – 3 < y + 1  ≤ 4y + 7, y R

2y – 3 – y < y + 1 – y ≤ 4y + 7 – y

y – 3 < 1 ≤ 3y + 7

y – 3 < 1 and 1 ≤3y + 7

y < 4 and 3y ≥ – 6  ⇒y ≥ – 2

– 2 ≤ y < 4

The graph of the given equation can be represented on a number line as:

Question 29

Solve the inequation:

3z – 5 ≤ z + 3 < 5z – 9, z  R.

Graph the solution set on the number line.

Answer 29

3z – 5 ≤ z + 3 < 5z – 9

3z – 5 ≤ z + 3 and z + 3 < 5z – 9

2z ≤ 8 and 12 < 4z

z ≤ 4 and 3 < z

Since, z € R

Solution set = {3 < z  4, Z  R }

It can be represented on a number line as:

Question 30

Solve the following in equation and represent the solution set on the number line.

Answer 30

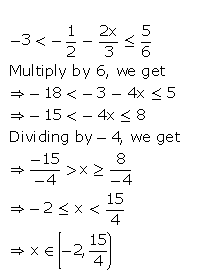
The solution set can be represented on a number line as:

Question 31

Solve the following in equation and represent the solution set on the number line:

Answer 31

Consider the given in  equation:

Question 32

Solve the following in equation, write the solution set and represent it on the number line:

Answer 32

Question 33

Answer 33

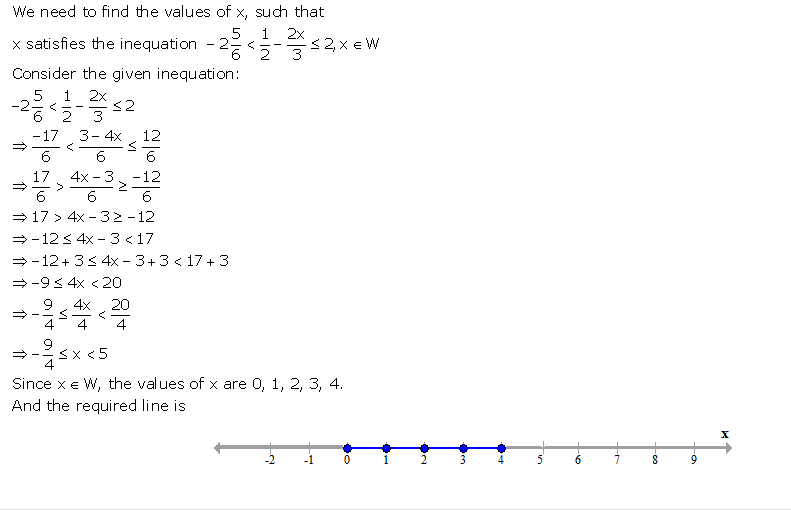
Question 34

Solve the following in equation and write the solution set:

13x – 5 < 15x + 4 < 7x + 12, x ∈ R

Represent the solution on a real number line.

Answer 34

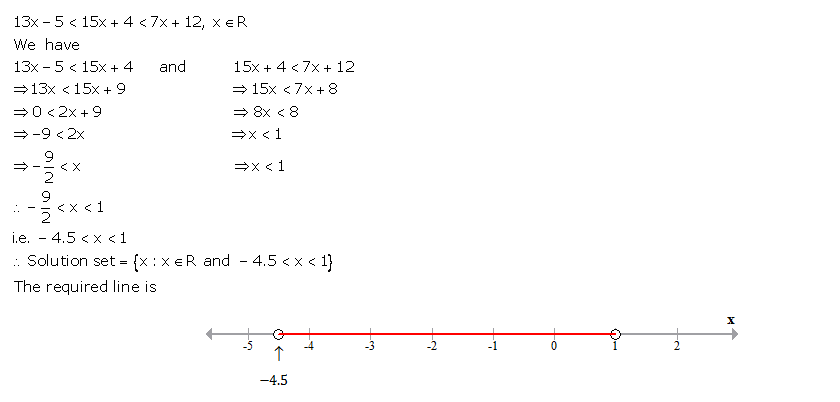
Question 35

Solve the following in equation, write the solution set and represent it on the number line.

Answer 35

Question 36

Solve the following in equation and represent the solution set on a number line.

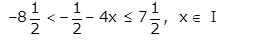
Answer 36

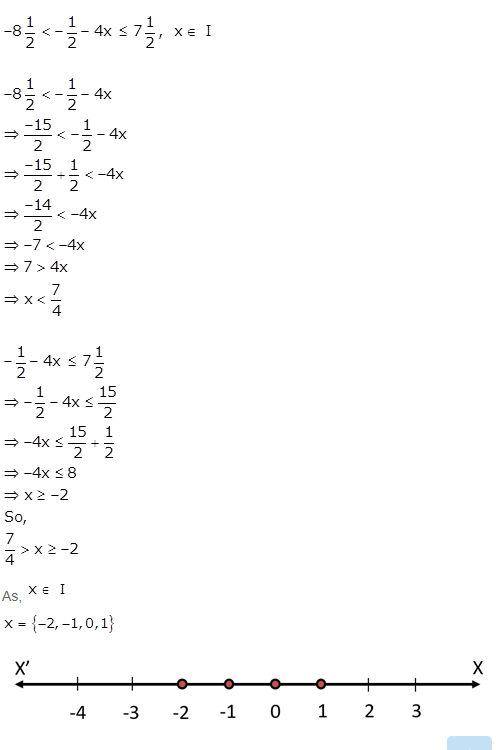
—–:End of Concise Solution Linear in Equations in One Variable Chapter 4 ICSE Class 10 :——

Return to :- Concise Selina  Maths Solutions for ICSE Class-10

Thanks

Please share with your friends