ML Aggarwal Similarity Exe-13.2 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-13.2 Questions for Similarity as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Similarity Exe-13.2 Class 10 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-13 | Similarity |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-13.2 |
| Academic Session | 2024-2025 |
Similarity Exe-13.2 Questions
ML Aggarwal Class 10 ICSE Maths Solutions
Question 1
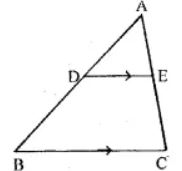
(a) In the figure (i) given below if DE || BG, AD = 3 cm, BD = 4 cm and BC = 5 cm. Find (i) AE : EC (ii) DE.
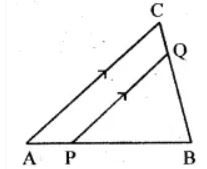
(b) In the figure (ii) given below, PQ || AC, AP = 4 cm, PB = 6 cm and BC = 8 cm. Find CQ and BQ.
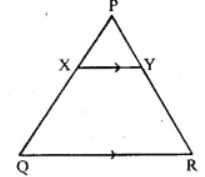
(c) In the figure (iii) given below, if XY || QR, PX = 1 cm, QX = 3 cm, YR = 4.5 cm and QR = 9 cm, find PY and XY.
Answer 1
(a) In the figure (i)
DE || BG, AD = 3 cm, BD = 4 cm and BC = 5 cm
(i) AE: EC
So, AD/BD = AE/EC
AE/EC = AD/BD
AE/EC = ¾
AE: EC = 3: 4
(ii) consider ∆ADE and ∆ABC
∠D = ∠B
∠E = ∠C
Therefore, ∆ADE ~ ∆ABC
Then, DE/BC = AD/AB
DE/5 = 3/(3 + 4)
DE/5 = 3/7
DE = (3 × 5)/7
DE = 15/7
DE = 2 (1/7)
(b) In the figure
PQ || AC, AP = 4 cm, PB = 6 cm and BC = 8 cm
∠BQP = ∠BCA … [because alternate angles are equal]
Also, ∠B = ∠B … [common for both the triangles]
Therefore, ∆ABC ~ ∆BPQ
Then, BQ/BC = BP/AB = PQ/AC
BQ/BC = 6/(6 + 4) = PQ/AC
BQ/BC = 6/10 = PQ/AC
BQ/8 = 6/10 = PQ/AC … [because BC = 8 cm given]
Now, BQ/8 = 6/10
BQ = (6/10) ×8
BQ = 48/10
BQ = 4.8 cm
Also, CQ = BC – BQ
CQ = (8 – 4.8) cm
CQ = 3.2cm
Hence, CQ = 3.2 cm and BQ = 4.8 cm
(c) In the figure
XY || QR, PX = 1 cm, QX = 3 cm, YR = 4.5 cm and QR = 9 cm,
So, PX/QX = PY/YR
1/3 = PY/4.5
By cross multiplication we get,
(4.5 × 1)/3 = PY
PY = 45/30
PY = 1.5
Then, ∠X = ∠Q
∠Y = ∠R
So, ∆PXY ~ ∆PQR
Hence, XY/QR = PX/PQ
XY/9 = 1/(1 + 3)
XY/9 = ¼
XY = 9/4
XY = 2.25
ML Aggarwal Similarity Exe-13.2 Class 10 ICSE Maths Solutions
Page 273
Question 2 In the given figure, DE || BC.
(i) If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, find the value of x.
(ii) If DB = x – 3, AB = 2x, EC = x – 2 and AC = 2x + 3, find the value of x.
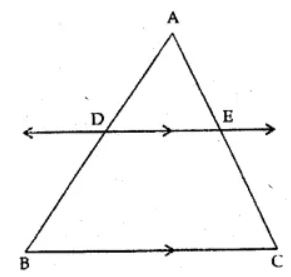
Answer 2 In the given figure, DE || BC
(i) Consider the ∆ABC,
AD/DB = AE/EC
x/(x – 2) = (x + 2)/(x – 1)
By cross multiplication we get,
X(x – 1) = (x – 2) (x + 2)
x2 – x = x2 – 4
-x = -4
x = 4
(ii) From the question it is given that,
DB = x – 3, AB = 2x, EC = x – 2 and AC = 2x + 3
Consider the ∆ABC,
AD/DB = AE/EC
2x/(x – 2) = (2x + 3)/(x – 3)
By cross multiplication we get,
2x(x – 2) = (2x + 3) (x – 3)
2x2 – 4x = 2x2 – 6x + 3x – 9
2x2 – 4x – 2x2 + 6x – 3x = -9
-7x + 6x = -9
-x = – 9
x = 9
Question 3 E and F are points on the sides PQ and PR respectively of a ∆PQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 8 cm and RF = 9 cm.
(ii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.
Answer 3
(i) In ∆PQR, E and F are the points on the sides PQ and PR respectively
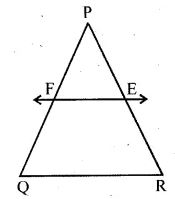
So, PE/EQ = 3.9/3
= 39/30
= 13/10
Then, PF/FR = 8/9
By comparing both the results,
13/10 ≠ 8/9
Therefore, PE/EQ ≠ PF/FR
So, EF is not parallel to QR
(ii) From the dimensions given in the question,
Consider the ∆PQR

So, PQ/PE = 1.28/0.18
= 128/18
= 64/9
PR/PF = 2.56/0.36
= 256/36
= 64/9
By comparing both the results,
64/9 = 64/9
Hence, PQ/PE = PR/PF
EF is parallel to QR.
Question 4 A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
Answer 4
In ∆PQR, A and B are points on the sides PQ and PR such that
PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm
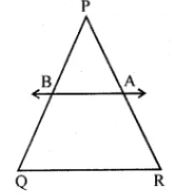
PQ/PA = 12.5/5
= 2.5/1
PR/PB = (PB + BR)/PB
= (4 + 6)/4
= 10/4, = 2.5
By comparing both the results,
2.5 = 2.5
Hence, PQ/PA = PR/PB
AB is parallel to QR.
Question 5
(a) In the figure (i) given below, CD || LA and DE || AC. Find the length of CL if BE = 4 cm and EC = 2 cm.
(b) In the given figure, ∠D = ∠E and AD/BD = AE/EC. Prove that BAC is an isosceles triangle.
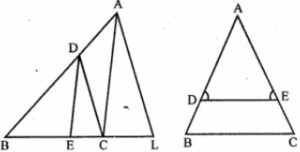
Answer 5
(a) From the figure, CD || LA and DE || AC,
Consider the ∆BCA,
BE/BC = BD/BA
By using the corollary of basic proportionality theorem,
BE/(BE + EC) = BD/AB
4/(4 + 2) = BD/AB … [equation (i)]
consider the ∆BLA
BC/BL = BD/AB
By using the corollary of basic proportionality theorem,
6/(6 + CL) = BD/AB … [equation (ii)]
combining the equation (i) and equation (ii), we get
6/(6 + CL) = 4/6
By cross multiplication we get,
6 x 6 = 4 x (6 + CL)
24 + 4CL = 36
4CL = 36 – 24
CL = 12/4
CL = 3 cm
Hence, the length of CL is 3 cm.
(b) From the figure, ∠D = ∠E and AD/BD = AE/EC,
We have to prove that, BAC is an isosceles triangle
So, consider the ∆ADE
∠D = ∠E … [from the question]
AD = AE … [sides opposite to equal angles]
Consider the ∆ABC,
AD/DB = AE/EC … [equation (i)]
Hence, DE parallel to BC
Because AD = AE
DB = EC … [equation (ii)]
By adding equation (i) and equation (ii) we get,
AD + DB = AE + EC
AB = AC
Hence, ∆ABC is an isosceles triangle.
ML Aggarwal Similarity Exe-13.2 Class 10 ICSE Maths Solutions
Question 6 In the adjoining given below, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. show that BC || QR.
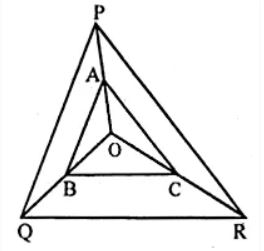
Answer 6
Consider the ∆POQ
AB || PQ … [given]
So, OA/AP = OB/BQ … [equation (i)]
Then, consider the ∆OPR
AC || PR
OA/AP = OC/CR … [equation (ii)]
Now by comparing both equation (i) and equation (ii),
OB/BQ = OC/CR
Then, in ∆OQR
OB/BQ = OC/CR
Hence, BC || QR
Question 7 ABCD is a trapezium in which AB || DC and its diagonals intersect each other at O. Using Basic Proportionality theorem, prove that AO/BO = CO/DO
Answer 7
Given : ABCD is a trapezium in which AB || DC
Its diagonals AC and BD intersect each other at O
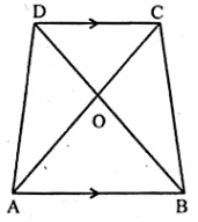
Now consider the ∆OAB and ∆OCD,
∠AOB = ∠COD [because vertically opposite angles are equal]
∠OBA = ∠ODC [because alternate angles are equal]
∠OAB = ∠OCD [because alternate angles are equal]
Therefore, ∆OAB ~ ∆OCD
Then, OA/OC = OB/OD
AO/OB = CO/DO … [by alternate angles]
Question 8 In the figure given below AD is bisector of ∠BAC. If AB = 6 cm, AC = 4 cm and BD = 3cm, find BC
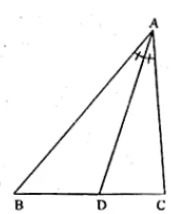
Answer 8
From the question it is given that,
AD is bisector of ∠BAC
AB = 6 cm, AC = 4 cm and BD = 3cm
Construction, from C draw a straight line CE parallel to DA and join AE
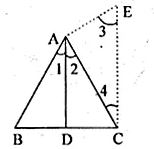
∠1 = ∠2 … [equation (i)]
By construction CE || DE
So, ∠2 = ∠4 … [because alternate angles are equal] [equation (ii)]
Again by construction CE || DE
∠1 = ∠3 … [because corresponding angles are equal] [equation (iii)]
By comparing equation (i), equation (ii) and equation(iii) we get,
∠3 = ∠4
So, AC = AE … [equation (iv)]
Now, consider the ∆BCE,
CE || DE
BD/DC = AB/AE
BD/DC = AB/AC
3/DC = 6/4
By cross multiplication we get,
3 × 4 = 6 × DC
DC = (3 × 4)/6
DC = 12/6
DC = 2
Hence, BC = BD + DC
= 3 + 2
= 5 cm
— : End of ML Aggarwal Similarity Exe-13.2 Class 10 ICSE Maths Solutions : –
Return to: ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


