ML Aggarwal Circle Exe-15.2 Class 9 ICSE Maths Solutions Ch-15. Step by Step Solutions of Exe-15.2 Questions on Circle of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Circle Exe-15.2 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-15 | Circle |
| Topics | Solution of Exe-15.2 Questions |
| Academic Session | 2024-2025 |
Solution of Exe-15.2 Questions on Circle
ML Aggarwal Class 9 ICSE Maths Solutions Ch-15
Question 1. If arcs APB and CQD of a circle are congruent, then find the ratio of AB: CD.
Answer : arc APB = arc CQD (given)
AB = CD (If two arcs are congruent, then their corresponding chords are equal)
Ratio of AB and CD = AB / CD = AB /AB = 1/1
AB : CD = 1 : 1
Question 2. A and B are points on a circle with centre O. C is a point on the circle such that OC bisects ∠AOB, prove that OC bisects the arc AB.
Answer : In a given circle with centre O,A
And B are Two points on the circle. C i
another point on the circle such that
∠AOC = ∠BOC
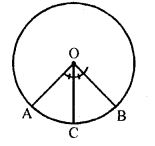
To prove : arc AC = arc BC
Proof: OC is the bisector of ∠AOB
⇒ ∠AOC = ∠BOC
But these are the angle subtended by the arc AC and BC
arc AC = arc BC.
Question 3. Prove that the angle subtended at the centre of a circle is bisected by the radius passing through the mid-point of the arc.
Answer : AB is the arc of the circle with
Centre O and C is the mid-Point od arc AB.
To prove: OC bisects the ∠AOB
I,e ∠AOC = ∠BOC
Proof: C is the mid-point of arc AB.
arc AC = arc BC

But arc AC and arc BC subtend ∠AOC and
∠BOC at the centre
∠AOC = ∠BOC
Hence, OC Bisects the ∠AOB.
Question 4. In the given figure, two chords AB and CD of a circle intersect at P. If AB = CD, prove that arc AD = arc CB.
Answer : given that Two chord AB and CD of a Circle Intersect at P and AB = CD
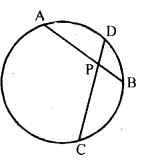
To prove : arc AD = arc CB
Proof: AB = CD
minor arc AB = minor arc CD
Subtracting arc BD from both sides
arc AB = arc BD = arc CD – arc BD
AD = arc CD
— : End of ML Aggarwal Circle Exe-15.2 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends