ML Aggarwal Circles Exe-15.2 Class 10 ICSE Maths Solutions

ML Aggarwal Circles Exe-15.2 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-15.2 Questions for Circles as council prescribe guideline for upcoming board exam. Visit official Website CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Circles Exe-15.2 Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	10th
Chapter-15	Circles
Writer / Book	Understanding
Topics	Solutions of Exe-15.2
Academic Session	2024-2025

ML Aggarwal Class 10 ICSE Maths Solutions

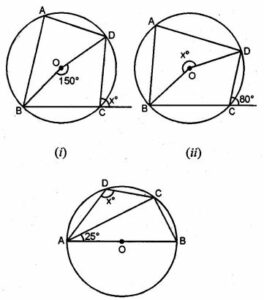
 Question 1. If O is the centre  of the circle, find the value of x in each of the following figures (using the given information):

Answer :

in figure
(i) ABCD is a cyclic quadrilateral

Ext. ∠DCE = ∠BAD

∠BAD = x^o

Now arc BD subtends ∠BOD at the center

And ∠BAD at the remaining part of the circle.

∠BOD = 2∠BAD = 2 x

⇒ 2x = 150^o (x = 75°)

(ii) ∠BCD + ∠DCE = 180^o (Linear pair)

⇒ ∠BCD + 80° = 180^o

⇒ ∠BCD = 180° – 80° = 100^o

Arc BAD subtends reflex ∠BOD at the

Centre and ∠BCD at the remaining part of the circle

Reflex ∠BOD = 2 ∠BCD

x^o = 2×100^o = 200^o

(iii) In ∆ACB,

∠CAB + ∠ABC + ∠ACB = 180^o (Angles of a triangle)

But ∠ACB = 90^o (Angles of a semicircle)

25^o + 90^o + ∠ABC = 180^o

⇒ 115^o + ∠ABC = 180^o

⇒ ∠ABC = 180^o – 115° =65^o

ABCD is a cyclic quadrilateral

∠ABC + ∠ADC = 180^o (Opposite angles of a cyclic quadrilateral)

⇒ 65^o + x^o =180^o

⇒ x^o = 180^o – 65^o = 115^o

Question 2.

 (a) In the figure (i) given below, O is the centre of the circle. If ∠AOC = 150°, find (i) ∠ABC (ii) ∠ADC.
(b) In the figure (ii) given below, AC is a diameter of the given circle and ∠BCD = 75°. Calculate the size of (i) ∠ABC (ii) ∠EAF.

Answer :

(a) Given, ∠AOC = 150° and AD = CD

We know that an angle subtends by an arc of a circle at the centre is twice the angle subtended by the same arc at any point on the remaining part of the circle.

(i) ∠AOC = 2×∠ABC

∠ABC = ∠AOC/2 = 150^o/2 = 75^o

(ii) From the figure, ABCD is a cyclic quadrilateral

∠ABC + ∠ADC = 180^o (Sum of opposite angels in a cyclic quadrilateral is 180^o)

⇒ 75^o + ∠ADC = 180^o

⇒ ∠ADC + 180^o – 75^o

⇒ ∠ADC = 105^o

(b) (i) as AC is the diameter of the circle

∠ABC = 90^o (Angle in a semi-circle)

(ii) ABCD is a cyclic quadrilateral

∠BAD + ∠BCD = 180^o

⇒ ∠BAD + 75^o = 180^o (∠BCD = 75^o)

⇒ ∠BAD = 180^o – 75^o = 105^o

But ∠EAF = ∠BAD (Vertically opposite angles)

∠EAF = 105^o

---

Circles Exe-15.2

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 338)

Question 3.

 (a) In the figure, (i) given below, if ∠DBC = 58° and BD is a diameter of the circle, calculate:
(i) ∠BDC (ii) ∠BEC (iii) ∠BAC

(b) In the figure (if) given below, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°. Find:
(i) ∠CAD (ii) ∠CBD (iii) ∠ADC (2008)

Answer :

(a) ∠DBC = 58°

BD is diameter

∠DCB = 90° (Angle in semi-circle)

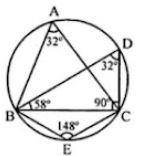
(i) In ∆BDC

∠BDC + ∠DCB + ∠CBD = 180°

⇒ ∠BDC = 180°- 90° – 58° = 32°

(ii) BEC = 180^o – 32^o = 148^o (opposite angles of cyclic quadrilateral)

(iii) ∠BAC = ∠BDC = 32^o (Angles in same segment)

(b) in the figure, AB ∥DC

∠BCE = 80^o and ∠BAC = 25^o

ABCD is a cyclic Quadrilateral and DC is

Production to E

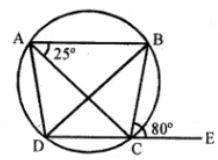
(i) Ext, ∠BCE = interior ∠A

⇒ 80^o = ∠BAC + ∠CAD

⇒ 80^o = 25^o + ∠CAD

⇒ ∠CAD = 80^o – 25^o = 55^o

(ii) But ∠CAD = ∠CBD (Alternate angels)

∠CBD = 55^o

(iii) ∠BAC = ∠BDC (Angles in the same segments)

∠BDC = 25^o (∠BAC = 25^o)

Now AB ∥ DC and BD is the transversal

∠BDC = ∠ABD

⇒ ∠ABD = 25^o

⇒ ∠ABC = ∠ABD + ∠CBD = 25^o + 55^o = 80^o

But ∠ABC + ∠ADC = 180^o (opposite angles of a cyclic quadrilateral)

⇒ 80^o + ∠ADC = 180^o

⇒ ∠ADC = 180^o – 80^o = 100^o

Question 4.

(a) In the figure given below, ABCD is a cyclic quadrilateral. If ∠ADC = 80° and ∠ACD = 52°, find the values of ∠ABC and ∠CBD.

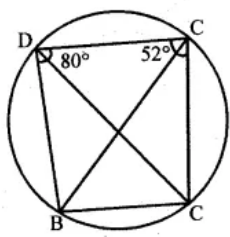
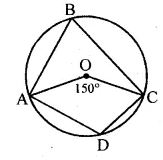
(b) In the figure given below, O is the centre of the circle. ∠AOE =150°, ∠DAO = 51°. Calculate the sizes of ∠BEC and ∠EBC.

Answer :

(a) In the given figure, ABCD is a cyclic quadrilateral

∠ADC = 80° and ∠ACD = 52°
To find the measure of ∠ABC and ∠CBD

ABCD is a Cyclic Quadrilateral

∠ABC + ∠ADC = 180^o (Sum of opposite angles = 180^o)
⇒ ∠ABC + 80^o = 180^o

∠AOE = 150^o, ∠DAO = 51^o

To find ∠BEC and ∠EBC

ABED is a cyclic quadrilateral

Ext. ∠BEC = ∠DAB = 51^o

⇒ ∠AOE = 150^o

⇒ Ref. ∠AOE = 360^o – 150^o = 51^o

⇒ ∠AOE = 150^o

⇒ Ref. ∠AOE = 360^o – 150^o = 210^o

Now, arc. ABE subtends ∠AOE at the Centre

And ∠ADE at the remaining part of the circle.

⇒ ∠ADE = ½ ref ∠AOE = ½ ×210^o = 105^o

But Ext. ∠EBC = ∠ADE = 105^o

Hence,

∠BEC = 51^o and ∠EBC = 105^o

(b) In the given figure, O is the centre of the circle.

∠AOE = 150°, ∠DAO = 51°

To find ∠BEC and ∠EBC

ABED is a cyclic quadrilateral

∴ Ext. ∠BEC = ∠DAB = 51°

∵ ∠AOE = 150°

∴ Ref. ∠AOE = 360° – 150° = 210°

Now arc ABE subtends ∠AOE at the centre and ∠AE at the remaining part of the circle.

∴ ∠ADE = ½ Ref. ∠AOE = 1/2 ×210° = 105°

But, Ext. ∠EBC = ∠ADE = 105°

Hence, ∠BEC = 51° and ∠EBC = 105°

Question 5.

(a) In the figure (i) given below, ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. Given that ∠BEF = 80°, find ∠ABC.
(b) In the figure (ii) given below, ABCD is a cyclic trapezium in which AD is parallel to BC and ∠B = 70°, find:
(i)∠BAD (ii) DBCD.

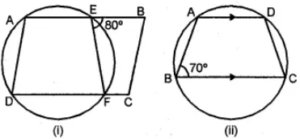
Answer :

(a) ADFE is a cyclic quadrilateral
Ext. ∠FEB = ∠ADF
⇒ ∠ADF = 80°
ABCD is a parallelogram
∠B = ∠D = ∠ADF = 80°
or ∠ABC = 80°
(b)In trapezium ABCD, AD || BC

(i) ∠B + ∠A = 180°

⇒ 70° + ∠A = 180°
⇒ ∠A = 180° – 70° = 110°
∠BAD = 110°

(ii) ABCD is a cyclic quadrilateral

∠A + ∠C = 180°
⇒ 110° + ∠C = 180°
⇒ ∠C = 180° – 110° = 70°
∠BCD = 70°

 Question 6.

 (a) In the figure given below, O is the centre of the circle. If ∠BAD = 30°, find the values of p, q and r.

(b) In the figure given below, two circles intersect at points P and Q. If ∠A = 80° and ∠D = 84°, calculate
(i) ∠QBC (ii) ∠BCP
Figure see in your text book

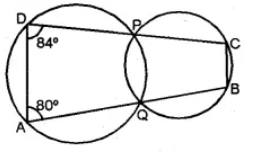
Answer :

(a)

(i) ABCD is a cyclic quadrilateral

∠A + ∠C = 180^o

⇒ 30^o + p = 180^o

⇒ p = 180^o – 30^o = 150^o

(ii) Arc BD subtends ∠BOD at the center

And ∠BAD at the remaining part of the circle

∠BOD = 2∠BAD

⇒ q = 2×30^o = 60^o

∠BAD = ∠BED are in the same segment of the circle

⇒ ∠BAD = ∠BED

⇒ 30^o = r

⇒ r = 30^o

AQPD is a cyclic quadrilateral

∠A + ∠QPD = 180^o

(b) Join PQ

AQPD is a cyclic quadrilateral

∴ ∠A + ∠QPD = 180^o

⇒ 80° + ∠QPD = 180°

⇒ ∠QPD = 180° – 80°

= 100°

And ∠D + ∠AQP = 180°

⇒ 84° + ∠AQP = 180°

⇒ ∠AQP = 180° – 84° = 96°

Now, PQBC is a cyclic quadrilateral,

∴ Ext. ∠QPD = ∠QBC

⇒ ∠QBC = 100°

And ext. ∠AQP = ∠BCP

⇒ ∠BCP = 96°

---

Circles Exe-15.2

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 339)

Question 7.

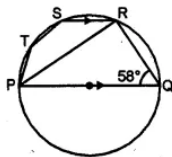
 (a) In the figure given below, PQ is a diameter. Chord SR is parallel to PQ. Given ∠PQR = 58°, calculate (i) ∠RPQ (ii) ∠STP
(T is a point on the minor arc SP)

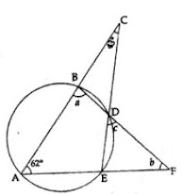
(b) In the figure given below, if ∠ACE = 43° and ∠CAF = 62°, find the values of a, b and c (2007)

Answer :

(a) In ∆PQR,

∠PRQ = 90° (Angle in a semi-circle) and ∠PQR = 58°

∠RPQ = 90° – ∠PQR = 90° – 58° = 32°

SR || PQ (given)

∠SRP = ∠RPQ = 32^o (Alternate angles)

Now, PRST is a cyclic quadrilateral,

∠STP + ∠SRP = 180^o

⇒ ∠STP = 180^o – 32^o = 148^o

(b) In the given figure,

∠ACE 43^o and ∠CAF = 62⁰

Now, in ∆AEC

∠ACE + ∠CAE + ∠AEC = 180^o

⇒ 43^o + 62^o + ∠AEC = 180^o

⇒ 105^o + ∠AEC = 180^o

⇒ ∠AEC = 180^o – 105° = 75^o

But ∠ABD + ∠AED = 180° (sum of opposite angles of acyclic quadrilateral) and,

∠AED = ∠AEC

⇒ a + 75^o = 180^o

⇒ a = 180^o – 75^o – 105^o

but ∠EDF = ∠BAE (Angles in the alternate segment)

Question 8.

(a) In the figure (i) given below, AB is a diameter of the circle. If ∠ADC = 120°, find ∠CAB.
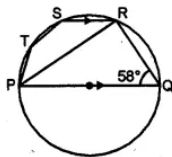
(b) In the figure (ii) given below, sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E, the sides AD and BC are produced to meet at F. If x : y : z = 3 : 4 : 5, find the values of x, y and z.

Answer :

(a) Construction: Join BC, and AC then
ABCD is a cyclic quadrilateral.

Ext. ∠2 = x + z and,

In ∆CBE,

Ext. ∠1 = x + y

Adding (i) and (ii)

x + y + x + z = ∠1 + ∠2

2 x + y + z = 180^o (ABCD is a cyclic quadrilateral)

But x : y : z = 3 : 4 : 5

x/y = ¾ (y = 4/3 x)

x/z = 3/5 (z = 5/3)

---

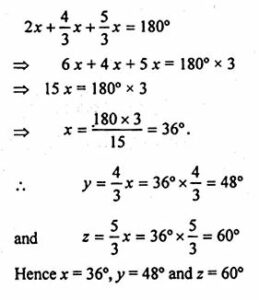
Circles Exe-15.2

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 340)

Question 9.

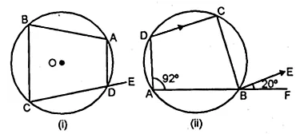
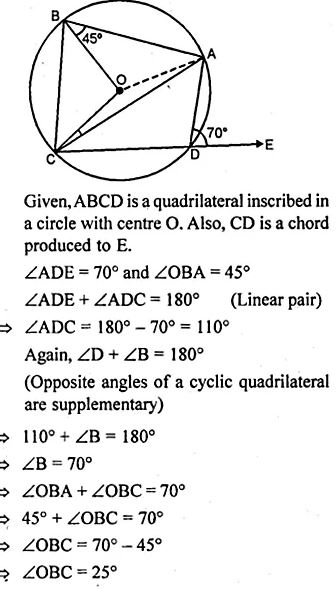
 (a) In the figure (i) given below, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E. If ∠ADE = 70° and ∠OBA = 45°, calculate
(i) ∠OCA (ii) ∠BAC
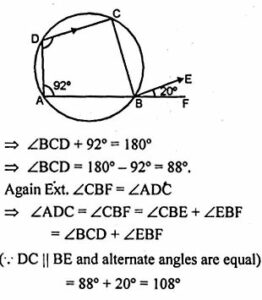
(b) In figure (ii) given below, ABF is a straight line and BE || DC. If ∠DAB = 92° and ∠EBF = 20°, find :
(i) ∠BCD (ii) ∠ADC.

Answer :

(a) ABCD is a cyclic quadrilateral

Question 10.

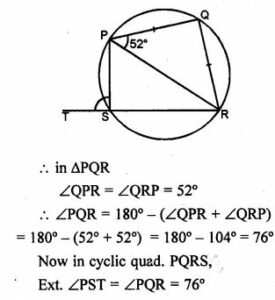
(a) In the figure (ii) given below, PQRS is a cyclic quadrilateral in which PQ = QR and RS is produced to T. If ∠QPR = 52°, calculate ∠PST.

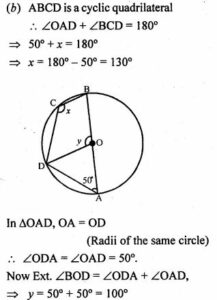
(b) In the figure (ii) given below, O is the centre of the circle. If ∠OAD = 50°, find the values of x and y.

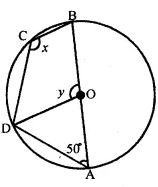
Answer :

(a) PQRS is a cyclic quadrilateral in which
PQ = QR

 Question 11.

(a) In the figure (i) given below, O is the centre of the circle. If ∠COD = 40° and ∠CBE = 100°, then find :
(i) ∠ADC
(ii) ∠DAC
(iii) ∠ODA
(iv) ∠OCA.
(b) In the figure (ii) given below, O is the centre of the circle. If ∠BAD = 75° and BC = CD, find :
(i) ∠BOD
(ii) ∠BCD
(iii) ∠BOC
(iv) ∠OBD (2009)

Answer :

(a) (i) ∴ ABCD is a cyclic quadrilateral.

∴ Ext. ∠CBE = ∠ADC
⇒ ∠ADC = 100°
(ii) Arc CD subtends ∠COD at the centre
and ∠CAD at the remaining part of the circle
∴ ∠COD = 2 ∠CAD

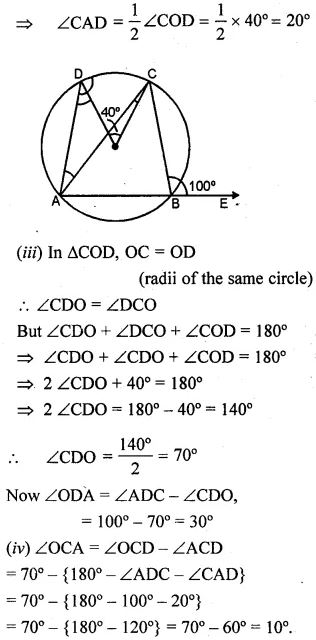
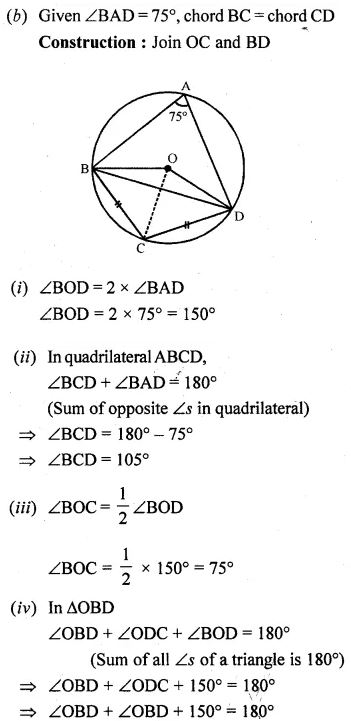
= 2∠OBD = 30°

= ∠OBD = 15°

---

Circles Exe-15.2

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 341)

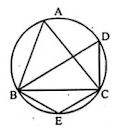
Question 12. In the adjoining figure, O is the centre and AOE is the diameter of the semicircle ABCDE. If AB = BC and ∠AEC = 50°, find :
(i) ∠CBE
(ii) ∠CDE
(iii) ∠AOB.
Prove that OB is parallel to EC.

Answer :

In the given figure,

O is the centre of the semi-circle ABCDE
and AOE is the diameter. AB = BC, ∠AEC = 50°

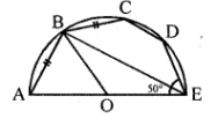
Question 13.

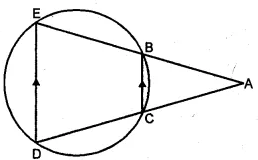
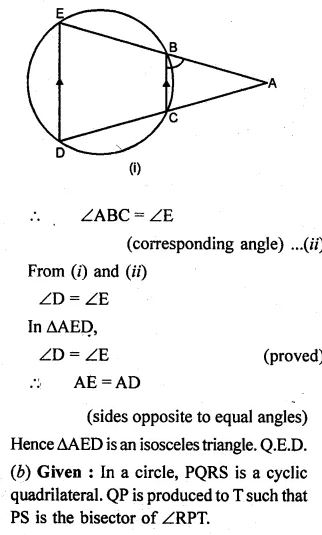
(a) In the figure (i) given below, ED and BC are two parallel chords of the circle and ABE, ACD are two st. lines. Prove that AED is an isosceles triangle.

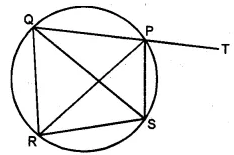
(b) In the figure (ii) given below, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = RS.

Answer :

(a) Given: Chord BC || ED,

ABE and ACD are straight lines.
To Prove: ∆AED is an isosceles triangle.
Proof: BCDE is a cyclic quadrilateral.
Ext. ∠ABC = ∠D …(i)
But BC || ED (given)

Question 14. In the adjoining figure, ABC is an isosceles triangle in which AB = AC and circle passing through B and C intersects sides AB and AC at points D and E. Prove that DE || BC.

Answer :

In the given figure,
∆ABC is an isosceles triangle in which AB = AC.
A circle passing through B and C intersects
sides AB and AC at D and E.
To prove: DE || BC
Construction : Join DE.
∵ AB = AC
∠B = ∠C (angles opposite to equal sides)
But BCED is a cyclic quadrilateral
Ext. ∠ADE = ∠C
= ∠B (∵ ∠C = ∠B)
But these are corresponding angles
DE || BC
Hence proved.

Question 15

(a) Prove that a cyclic parallelogram is a rectangle.
(b) Prove that a cyclic rhombus is a square.

Answer :

(a) ABCD is a cyclic parallelogram.

To prove: ABCD is a rectangle
Proof: ABCD is a parallelogram
∠A = ∠C and ∠B = ∠D

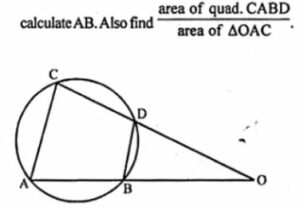
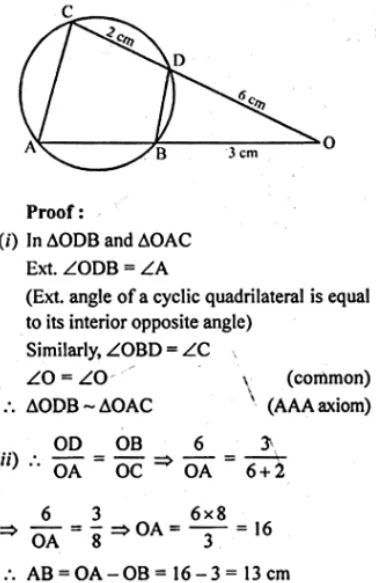
Question 16. In the adjoining figure, chords AB and CD of the circle are produced to meet at O. Prove that triangles ODB and OAC are similar. Given that CD = 2 cm, DO = 6 cm and BO = 3 cm, area of quad. CABD

Answer :

In the given figure, AB and CD are chords of a circle.
They are produced to meet at O.
To prove : (i) ∆ODB ~ ∆OAC
If CD = 2 cm, DO = 6 cm, and BO = 3 cm
To find : AB and also area of the

quad ABCD/area of ΔABC

Construction : Join AC and BD

—  : End of ML Aggarwal Circles Exe-15.2 Class 10 ICSE Maths Solutions : –

Return to:   ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends