Exponents ICSE Class-7th Concise Selina Maths Solutions Chapter-5. We provide step by step Solutions of Exercise / lesson-5 Exponents for ICSE Class-7 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-5 A and Exe-5 B, to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7.
Exponents ICSE Class-7th Concise Selina Maths Solutions Chapter-5
–: Select Topics :–
Exercise – 5 A Exponents ICSE Class-7th Concise Selina Maths Solutions
Question 1 :-
Find the value of:
(i) 6²
(ii) 73
(iii) 44
(iv) 55
(v) 83
(vi) 75
Answer :-

Question 2 :-
Evaluate:
(i) 23 x 42
(ii) 23 x 52
(iii) 33 x 52
(iv) 22 x 33
(v) 32 x 52
(vi) 53 x 24
(vii) 32 x 42
(ix) (5 x 4)2
Answer :-


Question 3 :-
Evaluate:

Answer :-

Question 4 :-
Evaluate :

Answer :-


Question 5 :-
Which is greater :
(i) 23 or 32
(ii) 25 or 52
(iii) 43 or 34
(iv) 54 or 45
Answer :-

Question 6 :-
Express each of the following in exponential form :
(i) 512
(ii) 1250
(iii) 1458
(iv) 3600
(v) 1350
(vi) 1176
Answer :-



Question 7 :-
If a = 2 and b = 3, find the value of:
(i) (a + b)2
(ii) (b – a)3
(iii) (a x b)a
(iv) (a x b)b
Answer :-

Question 8 :-
Express:
(i) 1024 as a power of 2.
(ii) 343 as a power of 7.
(iii) 729 as a power of 3.
Answer :-


Question 9 :-
If 27 x 32 = 3x x 2y; find the values of x and y.

Answer :-

Question 10 :-
If 64 x 625 = 2a x 5b; find :
(i) the values of a and b.
(ii) 2b x 5a
Answer :-


Exercise – 5 B Exponents ICSE Class-7th Concise Selina Mathematics
Question 1 :-
Fill in the blanks:
(i) In 52 = 25, base = ……… and index = ……….
(ii) If index = 3x and base = 2y, the number = ………
Answer :-
(i) In 52 = 25, base = 5 and index = 2.
(ii) If index = 3x and base = 2y, the number = 2y3x.
Question 2 :-
Evaluate:
(i) 28 ÷ 23
(ii) 23÷ 28
(iii) (26)0
(iv) (3o)6
(v) 83 x 8-5 x 84
(vi) 54 x 53 + 55
(vii) 54 ÷ 53 x 55
(viii) 44 ÷ 43 x 40
(ix) (35 x 47 x 58)0
Answer :-


Question 3 :-
Simplify, giving Solutions with positive index:


Answer :-



(xvii)
(2a3)4 (4a2)2
= (2a3)4 (22a2)2
= 24 a3×4 . 22×2 a2×2
= 24a12 . 24a4
= 24+4 a12+4
= 28a16
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × a16
= 256 a16
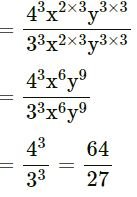
(xix)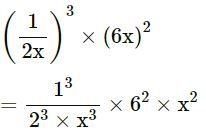



Question 4 :-
Simplify and express the Solution in the positive exponent form :


Answer :-
(i)
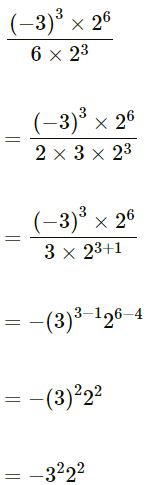
(ii) 
(iii)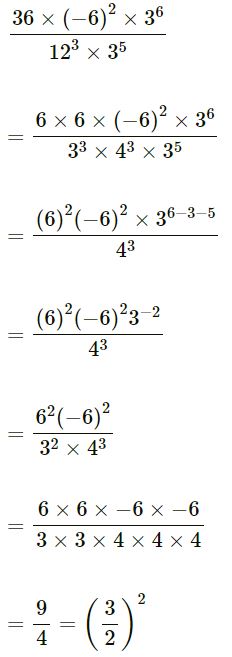
(iv)
-128/2187
| 2 | 128 |
| 2 | 64 |
| 2 | 32 |
| 2 | 16 |
| 2 | 8 |
| 2 | 4 |
| 2 | 2 |
| 1 |
| 3 | 2187 |
| 3 | 729 |
| 3 | 243 |
| 3 | 81 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
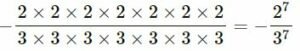
(v) 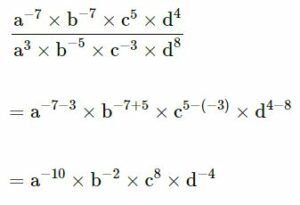
(vi) 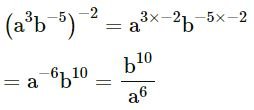
Question 5 :-
Evaluate

Answer :-

(iii)
53 × 32 + (17)0 × 73
= 5 × 5 × 5 × 3 × 3 + (17)0 × 7 × 7 × 7 (∵ a0 = 1)
= 125 × 9 + 1 × 343
= 1125 + 343 = 1468
(iv) 
(v)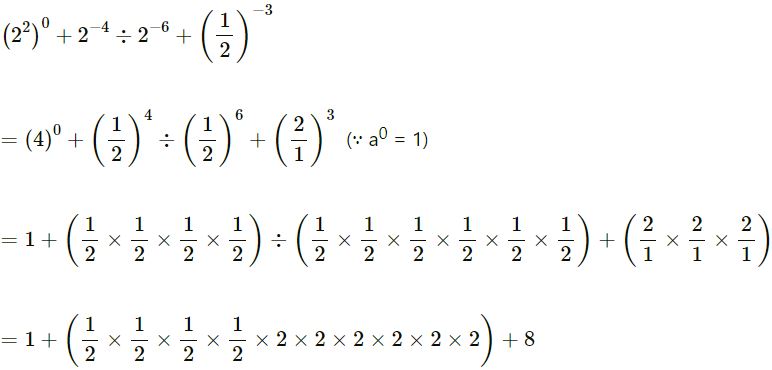
= 1 + 4 + 8 = 13
(vi) 
Question 6 :-
If m2 = -2 and n = 2; find the values of:
(i) m + r2 – 2mn
(ii) mn + nm
(iii) 6m-3 + 4n2
(iv) 2n3 – 3m
Answer :-

(iii)
6m-3 + 4n2
m = – 2, n =2
= 6(-2)-3 + 4(2)2

(iv)
2n3 – 3m
m = -2, n = 2
= 2(2)3 – 3(-2)
= 2 × (2 × 2 × 2) – 3 × (- 2)
= 16 – 3 × (-2)
= 16 + 6 = 22
— End of Exponents Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -7
Thanks