Factorisation ICSE Class-8th Concise Selina Mathematics

Factorisation ICSE Class-8th Concise Selina Mathematics Solutions Chapter- 13. We provide step by step Solutions of Exercise / lesson-13 Factorisation for ICSE Class-8 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-13 A,  Exe-13 B, Exe-13 C, Exe-13 D, Exe-13 E  and Exe-13 F to develop skill and confidence . Visit official Website CISCE for detail information about ICSE Board Class-8.

Factorisation ICSE Class-8th Concise Selina Mathematics Solutions Chapter- 13

---

–: Select Topics :–

 

Exe-13 A,

Exe-13 B,

Exe-13 C,

Exe-13 D,

Exe-13 E,

Exe-13 F,

 

---

 Exercise – 13 A Factorisation Solved Questions for ICSE Class-8th Concise Selina Publications

 

Factorise :

Question 1 :-

15x + 5
Answer:

15x + 5

= 5(3x + 1)

Question 2 :-

Answer

a³ – a² +a

= a(a² – a + 1)

Question 3 :-

Answer

Question 4 :-

Answer

Question 5 :-

Answer

Question 6 :-

Answer

Question 7 :-

Answer

Question 8:-

Answer

Question 9 :-

Answer

Question 10 :-

Answer

3x⁵y – 27x⁴y² + 12x³y³ 

= 3x³y (x² – 9xy + 4y²)

Question 11 :-

Answer

x²(a-b)-y² (a-b)+z²(a-b)

= (a – b)(x² – y² + z²)

Question 12 :-

Answer

(x + y)(a + b) + (x – y)(a + b)

= (a+b) (x + y + x – y)

= (a + b) (2x)

= 2x (a + b)

Question 13 :-

Answer

2b (2a + b) – 3c (2a + b)

= (2a + b) (2b – 3c)

Question 14 :-

Answer

12abc – 6a²b²c² + 3a³b³c³

= 3abc (4 – 2abc + a²b²c²)

Question 15 :-

Answer

4x(3x – 2y) – 2y(3x – 2y)

= (3x – 2y) (4x – 2y)

= (3x – 2y) × 2(2x – y)

= 2(3x – 2y) (2x – y)

Question 16 :-

Answer:

(a+ 2b) (3a + b) – (a+ b) (a+ 2b) +(a+ 2b)²

= (a + 2b) (3a + b – a – b + a + 2b)

= (a + 2b) (3a + 2b)

Question 17 :-

Answer

6xy(a² + b²) + 8yz(a² + b²) -10xz(a² + b²)

= H.C.F. of 6, 8, 10 = 2 , then

2(a² + b²) (3xy + 4yz – 5xz)

---

Selina Concise Maths Factorisation of ICSE Class-8th Exercise – 13 B 

 

Question 1 :-

Factorise : a² + ax + ab + bx
Answer :

a² + ax + ab + bx

= (a2 + ax) + (ab + bx)

= a(a + x) + b (a + x)

= (a + x) (a + b)

Question 2 :-

Factorise : a² – ab – ca + bc
Answer :

a² – ab – ca + bc

= a(a – b) – c(a – b)

= (a – b) (a – c)

Question 3 :-

Factorise : ab – 2b + a² – 2a
Answer

ab – 2b + a² – 2a

= b(a – 2) + a(a – 2)

= (a – 2) (b + a)

Question 4:-

Factorise : a³ – a² + a – 1
Answer

a³ -a² +a -1

= a² (a – 1) + 1 (a – 1)

= (a – 1) (a² + 1)

Question 5 :-

Factorise : 2a – 4b – xa + 2bx
Answer

2a – 4b – xa + 2bx

= 2 (a – 2b) – x (a – 2b)

= (a – 2b) (2 – x)

Question 6 :-

Answer

xy – ay – ax + a² + bx – ab

= y (x – a) – a (x – a) + b (x – a)

= (x – a) (y – a + b)

Question 7 :-

Answer

3x⁵ – 6x⁴ – 2x³ + 4x² + x – 2

= 3x⁴ (x – 2) – 2x² (x – 2) + 1 (x – 2)

= (x – 2) (3x⁴ – 2x² + 1)

Question 8 :-

Answer

– x²y – x + 3xy + 3

= 3 – x + 3xy – x²y

= 1(3 – x) + xy (3 – x)

= (3 – x) (1 + xy) = (xy + 1) (3 – x)

Question 9 :-

Answer

6a² – 3a²b – bc² + 2c² 

= 6a² – 3a²b + 2c² – bc²

= 3a² (2 – b) + c² (2 – b)

= (2 – b) (3a² + c²)

Question 10 :-

Answer

3a²b – 12a² – 9b + 36

= 3a² (b – 4) – 9 (b – 4)

= (b – 4) (3a² – 9) = (b – 4) 3 (a² – 3)

= 3 (b – 4) (a² -3)

Question 11 :-

Answer

x² – (a – 3)x – 3a

= x² – ax + 3x – 3a

= x (x – a) + 3 (x – a)

= (x – a) (x + 3)

Question 12 :-

Answer

Question 13 :-

Answer

a(b – c) – d(c – b)

= a (b – c) + d (b – c)

= (b – c) (a + d)

Question 14 :-

Answer

ab² – (a – c) b – c

= ab² – ab + bc – c

= ab (b – 1) + c (b – 1)

= (b – 1) (ab + c)

Question 15 :-

Answer

(a² – b²) c + (b² – c²)a

= a²c – b²c + ab2 – ac²

= a²c – ac² + ab² – b²c

= ac (a – c) + b² (a – c)

= (a – c) (ac + b²)

Question 16 :-

Answer

a³ – a² – ab + a + b – 1

= a³ – a² – ab + b + a – 1

= a² (a – 1) – b (a – 1) + 1 (a – 1)

= (a – 1) (a² – b + 1)

Question 17 :-

Answer

ab(c² + d²) – a²cd – b²cd

= abc² + abd² – a²cd – b²cd

= abc² – a²cd – b²cd + abd²

= ac (bc – ad) – bd (bc – ad)

= (bc – ad) (ac – bd)

Question 18 :-

Answer

2ab² – aby + 2cby – cy²

= 2b (ab + cy) – y (ab + cy)

= (ab + cy) (2b – y)

Question 19 :-

Answer

ax + 2bx + 3cx – 3a – 6b – 9c

= x (a + 2b + 3c) – 3 (a + 2b + 3c)

= (a + 2b + 3c) (x – 3)

Question 20 :-

Answer

2ab²c – 2a + 3b³c – 3b – 4b²c² + 4c

= 2a (b²c – 1) + 3b (b²c – 1) – 4c (b²c – 1)

= (b²c – 1) (2a + 3b – 4c)

---

Exercise – 13 C  Factorisation ICSE Class-8th Mathematics Solved

Question 1 :-

Factorise : 16 – 9x²
Answer

16 – 9x²

= (4)² – (3x)²

= (4 + 3x) (4 – 3x)  …[a² – b² = (a + b) (a – b)]

Question 2 :-

Factorise : 1 – 100a²
Answer

1 – 100a²

= = (1)² – (10a)²

= (1 + 10a) (1 – 10a)   …[a² – b² = (a + b) (a – b)]

Question 3 :-

Factorise : 4x² – 81y²
Answer

4x² – 81y² 

= (2x)² – (9y)²

= (2x + 9y) (2x – 9y) …[a² – b² = (a + b) (a – b)]

Question 4 :-

Answer

Question 5 :-

Factorise : (a+2b)² – a²
Answer

Question 6 :-

Answer

Question 7 :-

Answer:

Question 8 :-

Answer:

(5a – 2b)² – (2a – b)²

= (5a – 2b + 2a – b) (5a – 2b – 2a + b)

= (7a – 3b) (3a – b)

Question 9 :-

Answer:

1 – 25 (a+ b)²

= (1)² – [5(a+b)]²

= [1 + 5(a+b)] [1 – 5(a+b)]

= (1 + 5a + 5b) (1 – 5a – 5b)

Question 10 :-

Answer:

4(2a + b)² – (a – b)²

= [2(2a + b)]² – (a – b)²

= [2(2a + b) + a – b][2 (2a + b) -a + b]

= (4a + 2b + a – b)(4a + 2b – a + b)

= (5a + b)(3a + 3b)

= (5a + b) 3(a + b)

= 3 (5a + b) (a + b)

Question 11 :-

Answer:

25(2x + y)² – 16(x – y)²

= [5(2x + y)]² – [4(x-y)]²

= (10x + 5y)² – (4x – 4y)²

= (10x + 5y + 4x – 4y) (10x + 5y – 4x + 4y)

= (14x + y)(6x + 9y)

= (14x + y) 3(2x + 3y)

= 3 (14x + y)(2x + 3y)

Question 12 :-

Answer:

49(x – y)² -9(2x + y)²

= [7(x-y)]² – [3(2x + y)]²

= (7x – 7y)² – (6x + 3y)²

= (7x – 7y + 6x + 3y) (7x – 7y – 6x – 3y)

= (13x – 4y) (x – 10y)

Question 13 :-

Answer:

Question 14 :-

Evaluate :

Answer

Question 15 :-

Evaluate :
(0.7)² – (0.3)²
Answer

(0·7)² – (0·3)²

= (0.7 + 0.3) (0.7 – 0.3)  ….[a² – b² = (a + b) (a – b)]

= 1 × 0.4 = 0.4

Question 16 :-

Evaluate :
(4.5)² – (1.5)²
Answer

(4.5)² – (1.5)² 

= (4.5 + 1.5) (4.5 – 1.5) …[a² – b² = (a + b) (a – b)]

= 6 × 3 = 18

Question 17 :-

Answer

75(x + y)² – 48(x – y)²

= 3[25 (x + y)² – 16 (x – y)²]

= 3[{5 (x + y)²} – {4 (x – y)}²]

Using a² – b² = (a + b) (a – b)

= 3 [5(x + y) + 4(x – y)] [5(x + y) – 4(x – y)]

= 3 [5x + 5y + 4x – 4y] [5x + 5y – 4x + 4y]

= 3 (9x + y) (x + 9y)

Question 18 :-

Answer

a² + 4a + 4 – b²

….[(a + b)² = a² + 2ab + b²]
….[a² – b² = (a + b)(a – b)]

= (a)² + 2 × a × 2 + (2)² – (b)²

= (a + 2)² – (b)²

= (a + 2 + b) (a + 2 – b)

= (a + b + 2) (a – b + 2)

Question 19 :-

Answer

a² – b² – 2b – 1

= a² – (b² + 2b + 1)

…[(a + b)² = a² + b² + 2ab]
…[a² – b² = (a + b) (a – b)]

= (a)² – (b + 1)²

= (a + b + 1)(a – b – 1)

Question 20 :-

Answer

x² + 6x + 9 – 4y² 

= (x)² + 2 × x × 3 + (3)² – (2y)²

…[(a + b)² = a² + 2ab + b²]
…[a² – b² = (a + b)(a – b)]

= (x + 3)² – (2y)²

= (x + 3 + 2y) (x + 3 – 2y)

= (x + 2y + 3) (x – 2y + 3)

---

Selina Solutions Concise Mathematics Factorisation for ICSE Class-8th of Exercise – 13 D 

Question 1 :-

Answer

x² + 6x + 8

= x² + 4x + 2x + 8

= x(x + 4) + 2(x + 4)

= (x+4) (x+2)

Question 2 :-

Answer

x² + 4x + 3

= x² + 3x + x + 3

= x(x + 3) + 1 (x + 3)

= (x + 3) (x + 1)

Question 3 :-

Answer

a² +Sa+ 6

= a² + 3a + 2a + 6

= a(a + 3) + 2(a + 3)

= (a + 3)(a + 2)

Question 4 :-

Answer

a² – 5a+ 6

= a² – 3a – 2a + 6

= a(a – 3) – 2(a – 3)

= (a – 3)(a – 2)

Question5 :-

Answer

a² +5a – 6

= a2 + 6a – a – 6

= a (a + 6) – 1 (a + 6)

= (a + 6) (a – 1)

Question 6 :-

Answer

x² + 5xy + 4y²

= x² + 4xy + xy + 4y²

= x(x + 4y) + y (x + 4y)

= (x + 4y)(x + y)

Question 7 :-

Answer

a² – 3a- 40

= a² – 8a + 5a – 40

= a(a – 8) + 5(a – 8)

= (a – 8)(a + 5)

Question 8 :-

Answer

x² – x – 72

= x2 – 9x + 8x – 72

= x(x – 9) + 8(x – 9)

= (x – 9)(x + 8)

Question 9 :-

Answer

Question 10 :-

Answer

2a² + 7a + 6

= 2a² + 4a + 3a + 6

= 2a(a + 2) + 3(a + 2)

= (a + 2)(2a + 3)

Question 11 :-

Answer

3a² – 5a + 2

= 3a2 – 3a – 2a + 2

= 3a (a – 1) – 2(a – 1)

= (a – 1)(3a – 2)

Question 12 :-

Answer

7b² – 5b+ 1

= 7b² – 7b – b +1

= 7b(b – 1) – 1(b – 1)

= (b – 1)(7b – 1)

Question 13 :-

Answer

2a² – 17ab + 26b²

= 2a² – 13ab – 4ab + 26b²

= a(2a – 13b) – 2b(2a – 13b)

= (2a – 13b) (a – 2b)

Question 14 :-

Answer

2x² + xy – 6y²

= 2x² + 4xy – 3xy – 6y²

= 2x (x + 2y) – 3y(x + 2y)

= (x + 2y)(2x – 3y)

Question 15 :-

Answer

4c² + 3c – 10

= 4c² + 8c – 5c – 10

= 4c (c + 2) – 5(c + 2)

= (c + 2)(4c – 5)

Question 16 :-

Answer

14x² + x – 3

= 14x² + 7x – 6x – 3

= 7x (2x + 1) – 3(2x + 1)

= (2x + 1) (7x – 3)

Question 17 :-

Answer

6 + 7b – 3b²

= 6 + 9b – 2b – 3b²

= 3(2 + 3b) – b(2 + 3b)

= (2 + 3b)(3 – b)

Question 18 :-

Answer

5 + 7x – 6x²

= 5 + 10x – 3x – 6x²

= 5(1 + 2x) – 3x(1 + 2x)

= (1 + 2x)(5 – 3x)

Question 19 :-

Answer

4 + y – 14y²

= 4 + 8y – 7y – 14y²

= 4 (1 + 2y) – 7y (1 + 2y)

= (1 + 2y)(4 – 7y)

Question 20 :-

Answer:

5 + 3a – 14a²

5 + 10a – 7a – 14a²

= 5(1 + 2a) – 7a (1 + 2a)

= (1 + 2a) (5 – 7a)

Question 21 :-

Answer:

(2a + b)² + 5(2a + b) + 6

Let (2a + b) = x

(2a + b)² = x²

(2a + b)² + 5 (2a + b) + 6

= x² + 5x + 6

= x² + 3x + 2x + 6

= x(x + 3)+2(x + 3)

= (x + 3)(x + 2)

= (2a + b + 3)(2a + b + 2)
(Substituting the value of x)

Question 22 :-

Answer:

1 – (2x + 3y) – 6(2x + 3y)²

Let (2x + 3y) = a

∴ (2x + 3y)² = a²

∴ 1 – (2x + 3y) – 6(2x + 3y)²

= 1 – a – 6a²

= 1 – 3a + 2a – 6a²

= 1(1 – 3a) + 2a (1 – 3a)

= (1 – 3a) (1 + 2a)

= [1 – 3 (2x + 3y)][1 + 2(2x + 3y)]
(Substituting the value of a)

= (1 – 6x – 9y) (1 + 4x + 6y)

Question 23 :-

Answer:

(x – 2y)² – 12(x – 2y) + 32

Let (x – 2y) = a

∴ (x – 2y)² = a²

∴ (x – 2y)² – 12(x – 2y) + 32

= a² – 12a + 32

= a² – 8a – 4a + 32

= a(a – 8) – 4 (a – 8)

= (a – 8)(a – 4)

= (x – 2y – 8)(x – 2y – 4)
(Substituting the value of a)

Question 24 :-

Answer:

8 + 6(a + b) – 5(a + b)²

Let a + b = x

(a + b)² = x²

8 + 6 (a+b) – 5(a + b)²

= 8 + 6x – 5x²

= 8 + 10x – 4x – 5x²

= 2(4 + 5x) – x (4 + 5x)

= (4 + 5x)(2 – x)

= [4 + 5(a + b)] [2 – (a + b)]

(Substituting the value of x)

= [4 + 5a + 5b][2 – a – b]

Question 25 :-

Answer:

2(x + 2y)² – 5(x + 2y) + 2

Let x + 2y = a, then

2a² – 5a + 2

⇒ 2a² – a – 4a + 2

= a(2a – 1) – 2(2a – 1)

= (2a – 1)(a – 2)

= {2(x + 2y – 1)} {(x + 2y) – 2}

= (2x + 4y – 2)(x + 2y – 2)
…[∵ 2 × 2 = 4]
[-5 = -1-4]
[4 = (-1) × (-4)]

---

Exe – 13 E of Factorisation for ICSE Class-8th Concise Mathematics Answer

 

Question 1 :-

In each case find whether the trinomial is a perfect square or not:

Answer:

(i) 

x² + 14x + 49

= (x)² + 2 × x × 7 + (7)²

= (x + 7)²    …[a² + 2ab + b² =(a + b)²]

∴ The given trinomial x² + 14x + 49 is a perfect square.

(ii)

a² – 10a + 25

= (a)² – 2 × a × 5 + (5)²

= (a – 5)²   [∵ a² – 2ab + b² = (a – b)²]

∴ The given trinomial a² – 10a + 25 is a perfect square.

(iii)

4x² + 4x + 1

= (2x)² + 2 × 2x × 1 + (1)²

=(2x + 1)²     [∵ a² – 2ab + b² = (a – b)²]

∴ The given trinomial 4x² + 4x + 1 is a perfect square.

(iv)

9b² + 12b + 16

= (3b)² + 3b × 4 + (4)²

= x² + xy + y²  …[Taking 3b = x, and 4 = y]

(v)

16x² – 16xy + y² 

= (4x)² – 4 ×4x × y + (y)²

= a² – 4ab + b²

…[Taking 4x = a, and y = b]

∴ The given trinomial cannot be expressed as a² + 2ab + b² . Hence, it is not a perfect square.

(vi)

x² – 4x + 16

= (x)² – x × 4 + (4)²

= a – ab + b²

…[Taking x = a, and 4 = b]

∴ The given trinomial cannot be expressed as a² – 2ab + b². Hence, it is not a perfect square.

Question 2 :-

Factorise completely 2 – 8x².
Answer:

2 – 8x² = 2(1 – 4x²)

= 2[(1)² – (2x)²]

= 2(1 + 2x) (1 – 2x)

Question 3 :-

Factorise completely : 8x²y – 18y³
Answer:

8x²y – 18y³ = 2y (4x² – 9y²)

= 2y[(2x)² – (3y)²]

= 2y (2x + 3y) (2x – 3y)

Question 4 :-

Factorise completely : ax² – ay²
Answer:

ax² – ay² = a(x² – y²)

= a (x + y)(x – y)

Question 5 :-

Factorise completely : 25x³ – x
Answer:

25x³ – x = x (25x² – 1)

= x [(5x)² – (1)²]

= x (5x + 1)(5x – 1)

Question 6 :-

Factorise completely : a⁴ – b⁴
Answer:

a⁴ – b⁴ = (a2)2 – (b2)2

= (a² + b²) (a² – b²)

= (a² + b²)(a + b)(a – b)

Question 7 :-

Factorise completely : 16x⁴ – 81y⁴
Answer:

16x⁴ – 81y⁴  = (4x²)² – (9y²)²

= (4x² + 9y²) (4x² – 9y²)

= (4x² + 9y²)[(2x)² – (3y)²]

= (4x² + 9y²)(2x + 3y)(2x – 3y)

Question 8 :-

Factorise completely : 625 – x⁴
Answer:

625 – x⁴ = (25)² – (x²)²

= (25 + x²) (25 – x²)

= (25 + x²) [(5)² – (x)²]

= (25 + x²) (5 + x) (5 – x)

Question 9 :-

Factorise completely : x² – y² – 3x – 3y
Answer:

x² – y² – 3x – 3y = (x² – y²) – 3 (x + y)

= (x + y) (x – y) – 3(x + y)

= (x + y)(x – y -3)

Question 10 :-

Factorise completely : x² – y² – 2x + 2y
Answer:

x² – y² – 2x + 2y = (x² – y²) – 2(x – y)

= (x + y) (x – y) – 2(x – y)

= (x – y)(x + y – 2)

Question 11 :-

Factorise completely : 3x² + 15x – 72
Answer

3x² + 15x – 72 = 3 (x² + 5x – 24)

= 3[x² + 8x – 3x – 24]

= 3[x (x + 8) – 3 (x + 8)]

= 3[(x + 8)(x – 3)]

= 3 (x + 8)(x – 3)

Question 12 :-

Factorise completely : 2a² – 8a – 64
Answer

2a² – 8a – 64 = 2[a² – 4a – 32]

= 2[a² – 8a + 4a – 32]

= 2[a(a – 8) + 4(a – 8)]

= 2[(a – 8) (a + 4)]

= 2(a – 8)(a + 4)

Question 13 :-

Factorise completely : 5b² + 45b + 90
Answer

 

Question 14 :-

Factorise completely : 3x²y + 11xy + 6y
Answer

5b² + 45b + 90 = 5[b² + 9b + 18]

= 5[b² + 6b + 3b + 18]

= 5[b(b + 6) + 3(b + 6)]

= 5[(b + 6) (b + 3)]

= 5 (b + 6)(b + 3)

Question 15 :-

Factorise completely : 5ap² + 11ap + 2a
Answer

5ap² + 11ap + 2a = a[5p² + 11p + 2]

= a[5p² + 10p + p +2]

= a[5p(p+2) + 1(p + 2)]

= a[(p + 2)(5p + 1)]

= a (p + 2) (5p + 1)

Question 16 :-

Factorise completely : a² + 2ab + b² – c²
Answer

a² + 2ab + b² – c²
= (a² + 2ab + b²) – c²

= (a + b)2 – (c)²

= (a + b+ c) (a + b – c)

Question 17 :-

Factorise completely : x² + 6xy + 9y² + x + 3y
Answer

x² + 6xy + 9y² + x + 3y

= [(x)² + 2 × x × 3y + (3y)²] + (x + 3y)

= [x + 3y]² + (x + 3y)

= (x + 3y) (x + 3y) + (x + 3y)

= (x + 3y) (x + 3y + 1)

Question 18 :-

Factorise completely : 4a² – 12ab + 9b² + 4a – 6b
Answer

4a² -12ab + 9b² + 4a- 6b

= [(2a)² – 2 × 2a × 3b + (3b)²] + 2(2a – 3b)

= (2a – 3b)² + 2(2a – 3b)

= (2a – 3b)(2a – 3b + 2)

Question 19 :-

Factorise completely : 2a²b² – 98b⁴
Answer

2a²b² – 98b⁴ = 2b² (a² – 49b²)

= 2b² [(a)² – (7b)²]

= 2b² (a + 7b)(a – 7b)

Question 20 :-

Factorise completely : a² – 16b² – 2a – 8b
Answer

a² -16b² – 2a – 8b = [(a)⁴ – (4b)²] – 2(a + 4b)

= (a + 4b)(a – 4b) – 2(a + 4b)

= (a + 4b)(a – 4b – 2)

---

ICSE Class-8 Maths – Factorisation  Exercise – 13 F Selina Solutions

Question 1 :-

Factorise :

Answer

(i)

(ii) 

35a³b²c + 42ab²c²

= 7ab²c (5a² + 6c)

(iii)

(iv)

8(2a + 3b)³ – 12(2a + 3b)²

= 4 (2a + 3b)² [2 (2a + 3b) – 3]

= 4 (2a + 3b)² [4a + 6b – 3]

(v)

9a (x-2y)⁴ – 12a (x – 2y)³

= 3a (x – 2y)³ [3(x – 2y) – 4]

=3a(x – 2y)³ [3x -6y – 4]

Question 2 :-

Factorise :

Answer

(i)

a² – ab – 3a + 3b

= a (a – b) – 3 (a – b)

= (a – b) (a – 3)

(ii)

x²y – xy² + 5x – 5y

= xy (x – y) + 5 (x – y)

= (x – y) (xy + 5)

(iii)

a² – ab (1 – b) – b³ = a² – ab + ab² – b³

= a(a – b) + b² (a – b)

= (a – b) (a + b)²

(iv)

xy² + (x – 1) y – 1 = xy²+ xy – y – 1

= xy (y + 1) – 1 (y + 1)

= (xy – 1)(y + 1)

(v)

(ax + by)² + (bx – ay)²

= a²x² + b²y² + 2abxy + b²x² + a²y² – 2abxy

= a²x² + b²y² + b²x² + a²y²

= a²x² + a²y² + b²x² + b²y²

= a² (x² + y²) + b²(x² + y²)

= (x² + y²)(a² + b²)

(vi)

ab(x² + y²) – xy (a² + b²)

= abx² + aby² – a²xy – b²xy

= abx² – a²xy + aby² – b²xy

= abx² – a²xy – b²xy + aby² 

= ax (bx – ay) – by (bx – ay)

= (bx – ay)(ax – by)

(vii)

m – 1 – (m-1)² + am – a

= (m – 1) – (m – 1)² + a (m – 1)

= (m – 1) (1 – (m – 1) + a)

= (m – 1) (1 – m + 1 + a)

= (m – 1) (2 – m + a)

Question 3 :-

Factorise :

Answer

(i)

a² – (b – c)²

= (a – (b – c)) (a + b – c)  …[a² – b² = (a – b)(a + b)]

= (a – b + c) (a + b – c)

(ii)

25(2x – y)² – 16(x – 2y)²

= (5 (2x – y))² – (4 (x – 2y))²

= [5(2x – y) – 4 (x – 2y)][5(2x – y) + 4(x – 2y)]

= [10x – 5y – 4x + 8y][10x – 5y + 4x – 8y]
….[a² – b² = (a – b)(a + b)]

= (6x + 3y)(14x – 13y)

= 3(2x + y)(14x – 13y)

(iii)

16(5x + 4)² -9(3x – 2)²

= (4(5x + y))² – (3(3x – 2))²

= [4 (5x + 4) – 3 (3x – 2)] [4(5x + 4) +3(3x – 2)]
…..[a² – b² = (a – b)(a + b)]

= (20x + 16 – 9x + 6)(20x + 16 + 9x – 6)

= (11x + 22)(29x + 10)

= 11 (x + 2)(29x + 10)

(iv) 

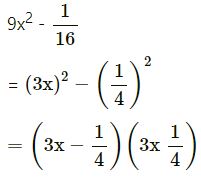
[(a² – b²) = (a – b)(a + b)] 

(v)

Question 4 :-

Factorise :

Answer

(i)

a² – 23a + 42  …[42 = 21 × 2 and 21 + 2 = 23]

= a² – 21a – 2a + 42

= a(a – 21) – 2(a – 21)

= (a – 21)(a – 2)

(ii)

a² – 23a -108

= a² – 27a + 4a – 108  …[27 × 4 = 108 and 27 -4 = 23]

= a(a – 27) + 4(a – 27)

= (a – 27)(a + 4)

(iii)

(iv)

5x² – 4xy – 12y²

= 5x² – 10xy + 6xy – 12y²

= 5x (x – 2y) + 6y (x – 2y)

= (x – 2y)(5x + 6y)

(v)

x(3x + 14) + 8

= 3x² + 14x + 8

= 3x² + 12x +2x +8

= 3x(x + 4) + 2(x + 4)

= (x + 4)(3x + 2)

(vi)

5 – 4x(1 + 3x)

= 5 – 4x – 12x²

= 5 – 10x + 6x – 12x²

= 5(1 – 2x)+ 6x (1 – 2x)

= (1 – 2x)(5 + 6x)

(vii)

x²y² – 3xy – 40

= x²y² – 8xy + 5xy – 40

= xy (xy – 8) + 5 (xy – 8)

= (xy – 8)(xy + 5)

(viii)

(3x – 2y)² – 5(3x – 2y) – 24

= (3x – 2y)² – 8(3x – 2y) + 3(3x – 2y) – 24

= (3x – 2y) (3x – 2y – 8) + 3 (3x – 2y – 8)

= (3x – 2y – 8)(3x – 2y + 3)

(ix)

12(a + b)² – (a+ b) – 35

= 12 (a + b)² – 21 (a + b) + 20 (a + b) – 7

= 3(a + b) [4 (a + b) – 7] + 5[4 (a + b) – 7]

= (4a + 4b – 7)(3a + 3b + 5)

Question 5 :-

Factorise :

Answer

(i)

15(5x – 4)² – 10(5x – 4)

= 5(5x – 4) [3(5x – 4)² – 2]

= 5 (5x – 4) [3 (25x² – 40x + 16) – 2]

= 5(5x – 4) (75x² – 120x + 46)

(ii)

3a²x – bx + 3a² – b

= x(3a² – b) + 1 (3a² – b)

= (x + 1)(3a² – b)

(iii)

b(c – d)² + a(d – c) + 3(c – d)

= b (c – d)² – a(c – d) + 3(c – d)

= (c – d) [b (c – d) – a + 3]

= (c – d) (bc – bd – a + 3)

(iv)

(v)

1 – 3x – 3y – 4(x + y)²

= 1 – 3(x + y) – 4(x + y)²

= 1 – 4(x + y) + (x + y) – 4(x + y)²

= 1[1 – 4(x + y)] + (x + y)[1 – 4(x + y)]

= [1 – 4x – 4y](1 + x + y)

Question 6 :-

Factorise :


Answer

(i)

2a³ – 50a

= 2a (a² – 25) = 2a(a² – 5²)

= 2a (a – 5) (a + 5)

(ii)

54a²b² – 6

= 6(9a²b² – 1) = 6[(3ab)² – (1)²]

= 6 (3ab – 1)(3ab + 1)

(iii)

64a²b – 144b³

= 16b (4a² – 9b²)

= 16b [(2a)² – (3b)²]

= 16b (2a + 3b)(2a – 3b)

(iv)

(2x – y)³ – (2x – Y)

= (2x – y)[(2x – y)² – 1]

= (2x – y)(2x – y – 1) (2x – y + 1)

(v)

x² – 2xy + y² – z²

= (x² – 2xy + y²) – z²

= (x – y)² – (z)²

= (x – y – z)(x – y + z)

(vi)

x² – y² – 2yz – z²

= x² – (y² + 2yz + z²)

= x² – (y + x)²

= (x – y – z)(x + y + z)

(vii)

7a⁵ – 567a

= 7a(a⁴ – 81)

= 7a (a²)² – (9)²

= 7a (a² + 9) (a² – 9)

= 7a (a² + 9) ((a)² – (3)²)

= 7a (a² + 9) (a + 3)(a – 3)

(viii)

7a⁵ – 567a

= 7a(a⁴ – 81)

= 7a (a²)² – (9)²

= 7a (a² + 9) (a² – 9)

= 7a (a² + 9) ((a)² – (3)²)

= 7a (a² + 9) (a + 3)(a – 3)

Question 7 :-

Factorise xy² – xz², Hence, find the value of:

Answer

(i)

xy² – xz² = x(y² – z²) = x(y – z)(y + z)

9 x 8² – 9 x 2²

= 9 (8² – 2²)

= 9(8 – 2)(8 + 2)

= 9 (6) (10) = 540

(ii)

xy² – xz² = x(y² – z²) = x(y – z)(y + z)

40 x 5.5² – 40 x 4.5²

= 40 (5.5)² – (4.5)²

= 40 (5.5 – 4.5) (5.5 + 4.5)

= 40 (1) (10) = 400

Question 8 :-

Factorise :

Answer

(i)

(a – 3b)² – 36 b²

= (a – 3b)² – (6b)²

= (a – 3b + 6b) (a – 3b – 6b)

= (a + 3b)(a – 9b)  ….[a² – b² = (a + b)(a – b)]

(ii)

25(a – 5b)² – 4(a – 3b)²

= [5 (a – 5b)]² – [2(a – 3b)]²

= (5a – 25b)² – (2a – 6b)² 

= (5a – 25b + 2a – 6b)(5a – 25b – 2a + 6b)
…..[a² – b² = (a + b)(a – b)]

= (7a – 31b)(3a – 19b)

(iii)

a² – 0·36 b²

=  (a)² – (0.6b)²

= (a + 0.6b)(a – 0.6b)      …[a² – b² = (a + b)(a – b)]

(iv)

a⁴ – 625

= (a²)² – (25)²

= (a² + 25) (a² – 25)    ….[a² – b² = (a + b)(a – b)]

= (a² + 25) {(a)² – (5)²}

= (a² + 25) (a + 5)(a – 5)

(v)

x⁴ – 5x² – 36

= (x²)² – 5x² – 36

= (x²)² – 9x² + 4x² – 36    …{∵ -36 = -9 × 4 }
{-5 = -9 + 4}

= x² (x² – 9) +  (x² – 9)

= (x² – 9)(x² + 4)

= [x² – (3)²] [x² + 4]

= (x + 3)(x – 3)(x² + 4)

= (x² +4) (x + 3)(x – 3)

(vi)

15(2x – y)² – 16(2x – y) – 15

= Let 2x – y = a, then

15a² – 16a – 15

= 15a² – 25a + 9a – 15
…{15 × (-15) = -225 , -225 = -25 × 9 , -16 = -25 + 9}

= 5a (3a – 5) + 3(3a – 5)

= (3a – 5)(5a + 3)

= [3 (2x – y) – 5][5 (2x – y) + 3]

= (6x – 3y – 5)(10x – 5y + 3)

Question 9 :-

Factorise a²b – b³ Using this result, find the value of 101² × 100 – 100³.
Answer

a²b – b³

b(a² – b²)

b(a + b)(a – b)

Now,

101² × 100 – 100³

= 100 (1012 – 100²)

= 100(101 + 100)(101 – 100)

= 100(201)(1)

= 20100

Question 10 :-

Evaluate (using factors): 301² × 300 – 300³.
Answer

301² x 300 – 300³

= 300 (301² – 300²)

= 300 (301 + 300)(301 – 300)

= 300 (601)(1)

= 180300

 

— End of Factorisation ICSE Class-8th Solutions :–

Return to – Concise Selina Maths Solutions for ICSE Class -8 

---