ML Aggarwal Factorisation Exe-6 Class 10 ICSE Maths Solutions Ch-6. We Provide Step by Step Answer of Exe-6 Questions for Factorisation as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Factorisation Exe-6 Class 10 ICSE Maths Solutions Ch-6
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-6 | Factorisation |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-6 |
| Academic Session | 2024-2025 |
ML Aggarwal Ch-6 Factorisation Exe-6
Class 10 ICSE Maths Solutions
Question -1. Find the remainder (without divisions) on dividing f(x) by x – 2, where
(i) f(x) = 5x2 – 7x + 4
(ii) f (x) = 2x3 – 7x2 + 3
Answer:
Let x – 2 = 0, then x = 2
(i) Substituting value of x in f(x)
f(x) = 5x2 – 7x + 4
⇒ f(2) = 5(2)2 – 7(2) + 4
= (5 × 4) – 14 + 4
= 20 – 14 + 4
= 24 – 14
= 10
(ML Aggarwal Factorisation Exe-6 Class 10 ICSE)
Question- 2. Using remainder theorem, find the remainder on dividing f(x) by (x + 3) where
(i) f(x) = 2x2 – 5x + 1
(ii) f(x) = 3x3 + 7x2 – 5x + 1
Answer :
(i) f(x) = 2x2 – 5x + 1
Let x + 3 = 0
⇒ x = -3
Substituting the value of x in f(x),
f(2)= (2 × 23) – (7 × 22) + 3
= (2 × 8) – (7 × 4) + 3
= 16 – 28 + 3
= 19 – 28
= -9
(ii) f(x) = 3x3 + 7x2 – 5x + 1
Let x + 3 = 0
Then, x = -3
Given, f(x) = 3x3 + 7x2 – 5x + 1
Now, substitute the value of x in f(x),
f(-3)= (3 × -33) + (7 × -32) – (5 × -3) + 1
= (3 × -27) + (7 × 9) – (-15) + 1
= – 81 + 63 + 15 + 1
= -81 + 79
= -2
Question -3. Find the remainder (without division) on dividing f(x) by (2x + 1) where
(i) f(x) = 4x2 + 5x + 3
(ii) f(x) = 3x3 – 7x2 + 4x + 11
Answer:
(i) f(x) = 4x2 + 5x + 3
Let 2x + 1 = 0
Then, 2x = -1
X = -½
Given, f(x) = 4x2 + 5x + 3
Now, substitute the value of x in f(x),
f (-½) = 4 (-½)2 + 5 (-½) + 3
= (4 × ¼) + (-5/2) + 3
= 1 – 5/2 + 3
= 4 – 5/2
= (8 – 5)/2
= 3/2 = 1½
(ii) f(x) = 3x3 – 7x2 + 4x + 11
Let 2x + 1 = 0
Then, 2x = -1
X = -½
Given, f(x) = 3x3 – 7x2 + 4x + 11
Now, substitute the value of x in f(x),
f(-½) = (3 × (-½)3) – (7 × (-½)2 + (4 × -½) + 11
= 3 × (-1/8) – (7 × ¼) + (- 2) + 11
= -3/8 – 7/4 – 2 + 11
= – 3/8 – 7/4 + 9
= (-3 – 14 + 72)/8
= 55/8
= 6(7/8)
(ML Aggarwal Factorisation Exe-6 Class 10 ICSE)
Question-4. Using remainder theorem, find the value of k if on dividing 2x3 + 3x2 – kx + 5 by x – 2, leaves a remainder 7.
Answer:
f(x) = 2x2 + 3x2 – kx + 5
g(x) = x – 2, if x – 2 = 0, then x = 2
Now, substitute the value of x in f(x),
f(2) = (2 × 23) + (3 × 22) – (k × 2) + 5
= (2 × 8) + (3 × 4) – 2k + 5
= 16 + 12 – 2k + 5
= 33 – 2k
given that, remainder = 7.
So, 7 = 33 – 2k
2k = 33 – 7
2k = 26
K = 26/2
K = 13
Question -5. Using remainder theorem, find the value of a if the division of x3 + 5x2 – ax + 6 by (x – 1) leaves the remainder 2a.
Answer :
Let x – 1 = 0, then x = 1
Substituting the value of x in f(x)
f(1) = 13 + (5 × 12) – (a × 1) + 6
= 1 + 5 – a + 6
= 12 – a
given that, remainder = 2a
So, 2a = 12 – a
2a + a = 12
3a = 12
a = 12/3
a = 4
Question -6
(i) What number must be subtracted from 2x2 – 5x so that the resulting polynomial leaves the remainder 2, when divided by 2x + 1 ?
(ii) What number must be added to 2x3 – 7x2 + 2x so that the resulting polynomial leaves the remainder – 2 when divided by 2x – 3?
Answer:
(i) Let a be subtracted from 2x2 – 5x,
Dividing 2x2 – 5x by 2x + 1,

given that, remainder = 2.
3 – p = 2
p = 3 – 2
p = 1
(ii) let ‘p’ be subtracted from 2x3 – 7x2 + 2x,

given that, remainder = – 2.
P – 6 = – 2
P = -2 + 6
P = 4
(ML Aggarwal Factorisation Exe-6 Class 10 ICSE)
Question -7
(i) When divided by x – 3 the polynomials x2 – px2 + x + 6 and 2x3 – x2 – (p + 3) x – 6 leave the same remainder. Find the value of ‘p’
(ii) Find ‘a’ if the two polynomials ax3 + 3x2 – 9 and 2x3 + 4x + a, leaves the same remainder when divided by x + 3.
(iii) the polynomial ax3 + 3x2 – 3 and 2x3 -5x + a, when divide by x-4 leave the reminder r1 and r2 respectively. if 2r1 = r2 find the value of a.
Answer:
(i) given that, by dividing x3 – px2 + x + 6 and 2x3 – x2 – (p + 3)x – 6 by x – 3 = 0,
then x = 3.
Let p(x) = x3 – px2 + x + 6
Now, substitute the value of x in p(x),
p(3) = 33 – (p × 32) + 3 + 6
= 27 – 9p + 9
= 36 – 9p
Then, q(x) = 2x3 – x2 – (p + 3)x – 6
Now, substitute the value of x in q(x),
q(3) = (2 × 33) – (3)2 – (p + 3) × 3 – 6
= (2 × 27) – 9 – 3p – 9 – 6
= 54 – 24 – 3p
= 30 – 3p
Given, that remainder is same in both case
So, 36 – 9p = 30 – 3p
36 – 30 = 9p – 3p
6 = 6p
p = 6/6
p = 1
(ii) Let p(x) = ax3 + 3x2 – 9 and q(x) = 2x3 + 4x + a
given that, both p(x) and q(x) leaves the same remainder when divided by x + 3.
Let x + 3 = 0
Then, x = -3
Now, substitute the value of x in p(x) and in q(x),
p(-3) = q(-3)
a(-3)3 + 3(-3)2 – 9 = 2(-3)3 + 4(-3) + a
-27a + 27 – 9 = – 54 – 12 + a
-27a + 18 = – 66 + a
-27a – a = -66 – 18
-28 a = -84
a = 84/28
a = 3
(iii) the polynomial ax3 + 3x2 – 3 and 2x3 -5x + a, when divide by x-4
ax3 + 3x2 – 3
r1 = a(4)3 + 3(4)2 – 3
= 64a + 48-3
= 64a + 45 ————–(i)
and
r2 = 2x3 -5x + a
= 2(4)3 -5(4) + a
= 128 – 20 +a
= 108 +a——————(ii)
but 2r1 = r2
2 x (64a + 45 ) = 108 +a
128a + 90 = 108 + a
128a – a = 108-90
127 a = 18
a = 18/127
(ML Aggarwal Factorisation Exe-6 Class 10 ICSE)
Question-8. Using reminder theorem find the reminder obtain when x3 + ( kx+8) x + k, is divided by x+1 and x-2 hence find k if the sum of the two remainders is 1 (2019)
Answer:
Given polynomial is p(x) = x3 +(kx + 8)x + k
g(x) = x + 1
∴ R1 = P(-1)
= (-1)3 + {k{-1} + 8} (-1) + k
= -1 + k – 8 + k
= 2k – 9
h(x) = x – 2
∴ R2 = P(2)
= (2)3 + (2k + 8)2 +k
= 8 + 4k + 16 + k
5k + 24
Now, R1 + R2 = 1
⇒ 2k – 9 + 5k + 24 = 1
⇒ 7k = 1 + 9 – 24
⇒ 7k = – 14
⇒ k = – 2
(ML Aggarwal Factorisation Exe-6 Class 10 ICSE)
Question-9. By factor theorem, show that (x + 3) and (2x – 1) are factors of 2x2 + 5x – 3.
Answer :
Let x + 3 = 0 then x = – 3
Substituting the value of x in f(x)
f(-3) = (2 × (-3)2) + (5 × -3) – 3
= (2 × 9) + (-15) – 3
= 18 – 15 – 3
= 18 – 18
= 0
Now, 2x – 1 = 0
Then, 2x = 1
x = ½
Given, f(x) = 2x2 + 5x – 3
Now, substitute the value of x in f(x),
f(½) = (2 × (½)2) + (5 × ½) – 3
= (2 × (¼)) + 5/2 – 3
= ½ + 5/2 – 3
= (1 + 5)/2 – 3
= 6/2 – 3
= 3 -3
= 0
Reminder = 0 hence proved that, (x + 3) and (2x – 1) both are factors
ML Aggarwal Ch-6 Factorisation Exe-6 Class 10 ICSE Maths Solutions
page-107
Question -10. Without actual division, prove that X4+2x3-2x2+2x-3 is exactly divisible by x2 +2x – 3.
Answer :
x2 + 2x – 3
= x2 + 3x – x – 3
= x(x + 3) – 1 (x + 3)
= (x + 3) (x – 1)
Let p(x) = x4 + 2x3 – 2x2 + 2x – 3
We see that
p(-3) = (-3)4 + 2(-3)3 – 2(-3)2 + 2(-3) – 3
= 81 – 54 – 18 – 6 – 3
= 0
Hence by converse of factor theorem, (x + 3) is a factor of p(x).
Also, we see that
p(1) = (1)4 + 2(1)3 – 2(1)2 + 2(1) – 3
= 0
Hence by converse of factor theorem, (x – 1) is a factor of p(x).
From above, we see that
(x + 3) (x – 1), i.e., x2 + 2x – 3 is a factor of p(x)
⇒ p(x) is exactly divisible by (x2 + 2x – 3).
Question -11. Show that (x – 2) is a factor of 3x2 – x – 10. Hence factorise 3x2 – x – 10.
Answer :
Let x – 2 = 0, then x = 2
Substituting the value of x in f(x),
f(x) = 3x2 – x – 10
= 3(2)2 – 2 – 10
= 12 – 2 – 10
= 0
∵ Remainder is zero
∴ x – 2 is a factor of f(x)
Dividing 3x2 – x – 10 by x – 2, we get
x-2)3x²-x-10(3x+5
3x2–6x
– +
———————
5x – 10
5x – 10
– +
———————
x
∴ 3x² – x – 10 = (x – 2)(3x + 5).
(ML Aggarwal Factorisation Exe-6 Class 10 ICSE)
Question -12. Using the factor theorem, show that (x – 2) is a factor of x3 + x2 – 4x – 4. Hence, factorise the polynomial completely. (2019)
Answer:
Given polynomial is p(x) = x3 + x2 – 4x – 4
x – 2 is its factor, if p(2) = 0
p(2) = (2)3 + (2)2 – 4(2) – 4 = 8 + 4 – 8 – 4 = 0
Thus, x – 2 is a factor of p(x).
Now, x3 + x2 – 4x + 4 = x2(x +1) – 4(x + 1)
= (x + 1) (x2 – 4)
= (x + 1) (x + 2) (x – 2)
Hence, the required factors are (x + 1), (x + 2) and (x – 2).
Question -13. Show that 2x + 7 is a factor of 2x3 + 5x2 – 11x – 14. Hence factorise the given expression completely, using the factor theorem. (2006)
Answer :
Let 2x + 7 = 0, then 2x = -7
x =
substituting the value of x in f(x),
f(-7/2) = 2(-7/2)3 + 5(-7/2)2 + 11(-7/2) – 14
= 2(-343/8) + 5(49/4) + (-77/2) – 14
= -343/4 + 245/4 – 77/2 – 14
= (-343 + 245 + 154 – 56)/4
= -399 + 399/4
= 0
Therefore, (2x + 7) is a factor of 2x3 + 5x2 – 11x – 14
Then, dividing f(x) by (2x + 1), we get

So 2x3 + 5x2 – 11x – 14 can be written in product of divisor and quotient
= (2x + 7)(x2 – x – 2)
= (2x + 7)[x2 – 2x + x – 2]
= (2x + 7)[x(x – 2) + 1(x – 2)]
= (2x + 7)(x + 1)(x – 2)
Question-14 Use factor theorem to factorise the following polynomials completely.
(i) x3 + 2x2 – 5x – 6
(ii) x3 – 13x – 12.
Answer :
(i) Let f(x) = x3 + 2x2 – 5x – 6
Factors of (∵ 6 = ± 1 : ± 2, ± 3, ±)
Let x = –1, then
f(–1) = (–1)3 + 2(–1)2 – 5(–1) – 6
= –1 + 2(1) + 5 – 6
= –1 + 2 + 5 – 6
= 7 – 7
= 0
∵ f(–1) = 0
∴ x + 1 is a factor of f(x)
Now, dividing f(x) by x + 1, we get
f(x) = (x + 1)(x2 + x – 6)
= (x + 1)(x2 + 3x – 2x – 6)
= (x + 1){x(x + 3) – 2(x + 3)
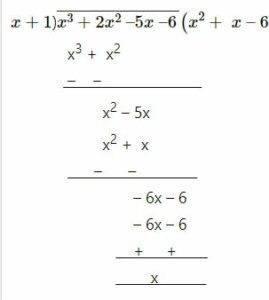
(ii) f(x) = x3 – 13x – 12
Let x = 4, then
f(x) = (4)3 – 13(4) – 12
= 64 – 52 – 12
= 64 – 64
= 0
∵ f(x) = 0
∴ x – 4 is a factor of f(x)
Now, dividing f(x) by (x – 4), we get
f(x) = (x – 4)(x2 + 4x + 3)
= (x – 4)(x2 + 3x + x + 3)
= (x – 4)[x(x + 3) + 1(x + 3)]
= (x – 4)(x + 3)(x + 1)

Question- 15. Use the Remainder Theorem to factorise the following expression
(i) 2x3 + x2 – 13x + 6. (2010)
(ii) 3x2 + 2x2 – 19x + 6 (2012)
(iii) 2x3 +3x2 – 9x – 10. (2018)
(iv) x3 +10x2 – 37x + 26 (2014)
Answer :
(i) Let f(x) = 2x3 + x2 – 13x + 6
Factors of 6 are ±1, ±2, ±3, ±6
Let x = 2, then
f(2) = (2 × 23) + 22 – 13 × 2 + 6
= (2 × 8) + 4 – 26 + 6
= 16 + 4 – 26 + 6
= 26 – 26
= 0
x – 2 is the factor of f(x) …(By Remainder Theorem)
Dividing f(x) by x – 2,

f(x) = (x – 2)(2x2 + 5x – 3)
= (x – 2){2x2 + 6x – x – 3}
= (x – 2){2x(x + 3) – 1(x + 3)}
= (x – 2)(x + 3)(2x – 1).
(ii) Let f(x) = 3x2 + 2x2 – 19x + 6
Using hit and trial method,
f(1) = 3 + 2 – 19 + 6 ≠ 0
f(−1) =–3 + 2 + 19 + 6 ≠ 0
f(2) = 24 + 8 – 38 + 6 = 0
Hence, (x – 2) is a factor of f(x)

(iii) 2x3 +3x2 – 9x – 10.
Let p(x) = 2x3 + 3x2 – 9x – 10
Factors of constant term 10 are ± 1, ± 2, ± 5
Put x = 2, we have
p(2) =2(2)3 + 3(2)2 – 9(2) – 10
= 16 + 12 – 18 – 10
= 0
∴ (x – 2) is a factor of p(x)
Put x = – 1, we have
P(-1) =2(-1)3 + 3(-1)2 – 9 (-1) – 10
= – 2 + 3 + 9 – 10 = 0
∴ (x + 1) is a factor of p(x)
Thus, (x + 1) (x – 2) i.e.,x2 – x – 2 is a factor of p(x)
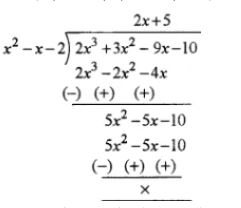
Hence, (x + 1), (x – 2) and (2x + 5) are the factors of given polynomial 2x3 + 3x2 – 9x – 10
(iv) x3 +10x2 – 37x + 26

On dividing x3 + 10x2 – 37x + 26 by x – 1, we get x2 + 11x – 26 as the quotient and remainder = 0.
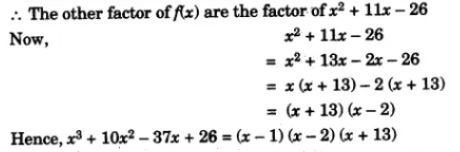
Question -16. If (2 x + 1) is a factor of 6x3 + 5x2 + ax – 2 find the value of a
Answer :
Let 2x + 1 = 0
Then, 2x = – 1
X = -½
Given, f(x) = 6x3 + 5x2 + ax – 2
substitute the value of x in f(x),
f (-½) = 6 (-½)3 + 5 (-½)2 + a (-½) – 2
= 6 (-1/8) + 5 (¼) – ½a – 2
= -3/4 + 5/4 – a/2 – 2
= (-3 + 4 – 2a – 8)/4
= (-6 – 2a)/4
, (2x + 1) is a factor of 6x3 + 5x2 + ax – 2
Then, remainder is 0.
So, (-6 – 2a)/4 = 0
-6 – 2a = 4 × 0
– 6 – 2a = 0
-2a = 6
a = -6/2
a = – 3
Question-17. If (3x – 2) is a factor of 3x3 – kx2 + 21x – 10, find the value of k.
Answer :
Let 3x – 2 = 0
Then, 3x = 2
X = 2/3
Given, f(x) = 3x3 – kx2 + 21x – 10
substitute the value of x in f(x),
f (2/3) = 3 (2/3)3 – k (2/3)2 + 21 (2/3) – 10
= 3 (8/27) – k (4/9) + 14 – 10
= 8/9 – 4k/9 + 14 – 10
= 8/9 – 4k/9 + 4
= (8 – 4k + 36)/9
= (44 – 4k)/9
(3x – 2) is a factor of 3x3 – kx2 + 21x – 10
Then, remainder is 0
So, (44 – 4k)/9 = 0
44 – 4k = 0 × 9
44 = 4k
K = 44/4
K = 11
Question -18. If (x – 2) is a factor of 2x3 – x2 + px – 2, then
(i) find the value of p.
(ii) with this value of p, factorize the above expression completely (2008)
Answer:
(i) Let x – 2 = 0, then x = 2
Now f(x) = 2x3 – x2 + px – 2
substitute the value of x in f(x),
f(2) = (2 × 23) – 22 + (p × 2) – 2
= (2 × 8) – 4 + 2p – 2
= 16 – 4 + 2p – 2
= 16 – 6 + 2p
= 10 + 2p
, (x – 2) is a factor of 2x3 – x2 + px – 2
Then, remainder is 0.
10 + 2p = 0
2p = – 10
P = -10/2
P = -5
So, (x – 2) is a factor of 2x3 – x2 + 5x – 2
(ii) 2x3 – x2 + 5x – 2 = (x – 2) (2x2 + 3x + 1)
= (x – 2) (2x2 + 2x + x + 1)
= (x – 2) (2x(x + 1) + 1(x + 1))
= (x + 1) (x – 2) (2x + 1)
Question -19. What number should be subtracted from 2x3 – 5x2 + 5x so that the resulting polynomial has 2x – 3 as a factor?
Answer :
Let P number to be subtracted from 2x3 – 5x2 + 5x
Then, f(x) = 2x3 – 5x2 + 5x – p
Given, 2x – 3 = 0
x = 3/2
f(3/2) = 0
So, f(3/2) = 2(3/2)3 – 5(3/2)2 + 5(3/2) – p = 0
2(27/8) – 5(9/4) + 15/2 – p = 0
27/4 – 45/4 + 15/2 – p = 0
27 – 45 + 30 – 4p = 0
57 – 45 – 4p = 0
12 – 4p = 0
P = 12/4
P = 3
(ML Aggarwal Factorisation Exe-6 Class 10 ICSE)
Question -20
(i) Find the value of the constants a and b, if (x – 2) and (x + 3) are both factors of the expression x3 + ax2 + bx – 12. (2001)
(ii) If (x+2) and (x+3) are factors of x3 + ax + b, Find the values of a and b.
Answer :
(i) Let x – 2 = 0
Then, x = 2
Given, f(x) = x3 + ax2 + bx – 12
substitute the value of x in f(x),
f(2) = 23 + a(2)2 + b(2) – 12
= 8 + 4a + 2b – 12
= 4a + 2b – 4
(x – 2) is a factor of x3 + ax2 + bx – 12.
So, 4a + 2b – 4 = 0
4a + 2b = 4
2a + b = 2 … (i)
Now, x + 3 = 0
Then, x = -3
Given, f(x) = x3 + ax2 + bx – 12
substitute the value of x in f(x),
f(-3) = (-3)3 + a(-3)2 + b(-3) – 12
= -27 + 9a – 3b – 12
= 9a – 3b – 39
(x – 3) is a factor of x3 + ax2 + bx – 12.
So, 9a – 3b – 39 = 0
9a – 3b = 39
3a – b = 13 … (ii)
, adding both equation (i) & (ii)
(2a + b) + (3a – b) = 2 + 13
2a + 3a + b – b = 15
5a = 15
a = 15/5
a = 3
Putting a = 3 inequation (i) to find ‘b’.
2a + b = 2
2(3) + b = 2
6 + b = 2
b = 2 – 6
b = -4
(ii) Let x + 2 = 0
Then, x = -2
Given, f(x) = x3 + ax + b
substitute the value of x in f(x),
f(-2) = (-2)3 + a(-2) + b
= -8 – 2a + b
(x + 2) is a factor of x3 + ax + b.
remainder is 0.
f(x) = 0
– 8 – 2a + b = 0
2a – b = – 8 … (i)
Let x + 3 = 0
Then, x = -3
Given, f(x) = x3 + ax + b
substitute the value of x in f(x),
f(-2) = (-3)3 + a(-3) + b
= -27 – 3a + b
(x + 3) is a factor of x3 + ax + b.
remainder is 0.
f(x) = 0
– 27 – 3a + b = 0
3a – b = – 27 … (i)
, subtracting
(2a – b) – (3a – b) = -8 – (-27)
2a – 3a – b + b = – 8 + 27
-a = 19
a = -19
Putting value of a = -19 inequation (i) to find ‘b’.
2a – b = – 8
2(-19) – b = -8
-38 – b = – 8
b = -38 +8
b = -30
(ML Aggarwal Factorisation Exe-6 Class 10 ICSE)
Question-21. If (x + 2) and (x – 3) are factors of x3 + ax + b, find the values of a and b. With these values of a and b, factorize the given expression.
Answer :
If x + 2 = 0, then x = -2
Substituting the value of x in f(x),
f(x) = x3 + ax + b
substitute the value of x in f(x),
f(-2) = (-2)3 + a(-2) + b
= -8 – 2a + b
(x + 2) is a factor of x3 + ax + b.
remainder is 0.
f(x) = 0
– 8 – 2a + b = 0
2a – b = – 8 … (i)]
let x – 3 = 0
Then, x = 3
Given, f(x) = x3 + ax + b
, substitute the value of x in f(x),
f(3) = (3)3 + a(3) + b
= 27 + 3a + b
From the question, (x – 3) is a factor of x3 + ax + b.
Therefore, remainder is 0.
f(x) = 0
27 + 3a + b = 0
3a + b = – 27……… (ii)
adding both equation (i) and (ii)
(2a – b) + (3a + b) = – 8 – 27
2a – b + 3a + b = -35
5a = -35
a = -35/5
a = -7
putting a = -7 in equation (i) to find ‘b’.
2a – b = – 8
2(-7) – b = -8
-14 – b = -8
b = – 14 + 8
b = -6
value of a = -7 and b = -6.
Then, f(x) = x3 – 7x – 6
(x + 2) (x – 3)
= x(x – 3) + 2(x – 3)
= x2 – 3x + 2x – 6
= x2 – x – 6
Dividing f(x) by x2 – x – 6 we get,
x3 – 7x – 6 = (x + 1) (x + 2) (x – 3)
Question -22. (x – 2) is a factor of the expression x3 + ax2 + bx + 6. When this expression is divided by (x – 3), it leaves the remainder 3. Find the values of a and b. (2005)
Answer :
As x – 2 is a factor of
f(x) = x3 + ax2 + bx + 6 ……..(i)
Let x – 2 = 0
Then, x = 2
substitute the value of x in f(x),
f(2) = 23 + a(2)2 + 2b + 6
= 8 + 4a + 2b + 6
= 14 + 4a + 2b
= 7 + 2a + b
(x – 2) is a factor of the expression x3 + ax2 + bx + 6.
So, remainder is 0.
f(x) = 0
7 + 2a + b = 0
2a + b = -7 … (ii)
given that when expression is divided by (x – 3), it leaves the remainder 3.
remainder = 33 + 9a + 3b = 3
9a + 3b = 3 – 33
9a + 3b = -30
= 3a + b = – 10 … (iii)
subtracting equation (iii) from equation (ii)
(3a + b) – (2a + b) = – 10 – (-7)
3a – 2a + b – b = – 10 + 7
a = -3
Putting a = -3 equation (ii) to find ‘b’.
2a + b = – 7
2(-3) + b = – 7
-6 + b = – 7
b = – 7 + 6
b = – 1
Question-23. If (x – 2) is a factor of the expression 2x3 + ax2 + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b. (2013)
Answer :
f(x) = 2x3 + ax2 + bx – 14
∴ (x – 2) is factor of f(x)
f(2) = 0
f(2) = 2(2)3 + a(2)2 + 2b – 14
= 16 + 4a + 2b – 14
= 2 + 4a + 2b
= 1 + 2a + b
R=0
2a + b = -1 … (i)
when expression is divided by (x – 3), it leaves the remainder 52.
∴ f(3) = 52
2(3)3 + a(3)2 + b(3) – 14 = 52
⇒ 54 + 9a + 3b – 14 = 52
⇒ 9a + 3b = 52 – 40
9a + 3b = 12
3a + b = 4 …(ii)
on Solving these (i) and (ii) simultaneous
2a + b = -1 … (i)
3a + b = 4 …(ii)
get value of a and b
a = 5
b= -2
(ML Aggarwal Factorisation Exe-6 Class 10 ICSE)
Question -24. If ax3 + 3x2 + bx – 3 has a factor (2x + 3) and leaves remainder – 3 when divided by (x + 2), find the values of a and 6. With these values of a and 6, factorise the given expression.
Answer :
Let , 2x + 3 = 0
Then, 2x = -3
x = -3/2
Given, f(x) = ax3 + 3x2 + bx – 3
substitute the value of x in f(x),
f(-3/2) = a(-3/2)3 + 3(-3/2)2 + b(-3/2) – 3
= a(-27/8) + 3(9/4) – 3b/2 – 3
= -27a/8 + 27/4 – 3b/2 – 3
given that, ax3 + 3x2 + bx – 3 has a factor (2x + 3).
remainder is 0.
-27a/8 + 27/4 – 3b/2 – 3 = 0
-27a + 54 – 12b – 24 = 0
-27a – 12b = -30
9a + 4b = 10 (i)
, let x + 2 = 0
Then, x = -2
Given, f(x) = ax3 + 3x2 + bx – 3
substitute the value of x in f(x),
f(2) = a(-2)3 + 3(-2)2 + b(-2) – 3
= -8a + 12 – 2b – 3
= -8a – 2b + 9
Leaves the remainder -3
So, -8a – 2b + 9 = -3
-8a – 2b = -3 – 9
-8a – 2b = -12
4a + b = 6 (ii)
By multiplying equation (ii) by 4,
16a + 4b = 24
Now, subtracting equation (ii) from equation (i) we get,
(16a + 4b) – (9a + 4b) = 24 – 10
16a – 9a + 4b – 4b = 14
7a = 14
a = 14/7
a = 2
put a = 2 equation (i) to find ‘b’.
9a + 4b = 10
9(2) + 4b = 10
18 + 4b = 10
4b = 10 – 18
4b = -8
b = -8/4
b = -2
Therefore, f(x) = ax3 + 3x2 + bx – 3
= 2x3 + 3x2 – 2x – 3
Given, 2x + 3 is a factor of f(x)
So, divide f(x) by 2x + 3

Therefore, 2x3 + 3x2 – 2x – 3 = (2x + 3) (x2 – 1)
= (2x + 3) (x + 1) (x – 1)
Question- 25. Given f(x) = ax2 + bx + 2 and g(x) = bx2 + ax + 1. If x – 2 is a factor of f(x) but leaves the remainder – 15 when it divides g(x), find the values of a and b. With these values of a and b, factorise the expression. f(x) + g(x) + 4x2 + 7x.
Answer:
given that, f(x) = ax2 + bx + 2 and g(x) = bx2 + ax + 1 and x – 2 is a factor of f(x),
, x = 2
substitute the value of x in f(x),
f(2) = 0
a(2)2 + b(2) + 2 = 0
4a + 2b + 2 = 0
2a + b + 1 = 0 … (i)
when, g(x) divide by (x – 2), leaves remainder = – 15
g(x) = bx2 + ax + 1
So, g(2) = -15
b(2)2 + 2a + 1 = -15
4b + 2a + 1 + 15 = 0
4b + 2a + 16 = 0
2b + a + 8 = 0 … (ii)
Now, subtracting equation (ii) from equation (i) multiplied by 2,
(4a + 2b + 2) – (a + 2b + 8) = 0 – 0
4a – a + 2b – 2b + 2 – 8 = 0
3a – 6 = 0
3a = 6
a = 6/3
a = 2
let the equation (i) to find ‘b’.
2a + b + 1 = 0
2(2) + b = – 1
4 + b = – 1
b = – 1 – 4
b = – 5
Now, f(x) = ax2 + bx + 2 = 2x2 – 5x + 2
g(x) = bx2 + ax + 1 = -5x2 + 2x + 1
then, f(x) + g(x) + 4x2 + 7x
= 2x2 – 5x + 2 – 5x2 + 2x + 1 + 4x2 + 7x
= x2 + 4x + 3
= x2 + 3x + x + 3
= x(x + 3) + 1(x + 3)
= (x + 1) (x + 3)
— : End of ML Aggarwal Factorisation Exe-6 Class 10 ICSE Maths Solutions Ch-6 : –
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends