Linear Equations Class-7 ML Aggarwal ICSE Mathematics Solutions Chapter-9. We provide step by step Solutions of Exercise / lesson-9 Linear Equations and Inequalities ICSE Class-7th ML Aggarwal Maths.
Our Solutions contain all type Questions with Exe-9.1 , Exe-9.2, Exe-9.3 Objective Type Questions ( including Mental Maths Multiple Choice Questions Value Based Questions, HOT) and Check Your Progress to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7 Mathematics.
Linear Equations Class-7 ML Aggarwal ICSE Mathematics Solutions with Inequalities Chapter-9
–: Select Topic :–
Objective Type Questions, Mental Maths,
Multiple Choice Questions ,(MCQ)
Exercise-9.1, Linear Equations and Inequalities Class-7 ML Aggarwal ICSE Mathematics Solutions
Solve the following ( 1 to 9 ) equations
Question 1.
(i) 2 (3 – 2x) = 13
(ii) 3⁄5 y – 2 = 7⁄10
Answer-1

Question 2
(i)…x⁄2…= 5 + …x⁄3.
(ii) 2 (x – 3⁄2)…= 11….
Answer-2
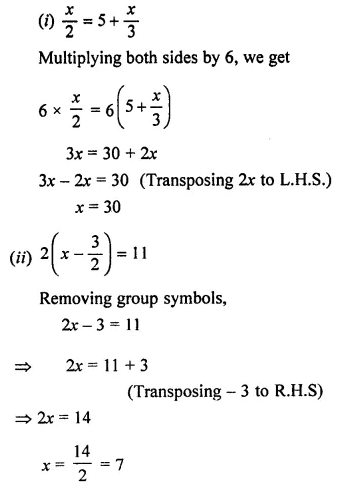
Question 3.
(i) 7(x – 2) = 2 (2x – 4)
(ii) 21 – 3(x – 7) = x + 20
Answer-3
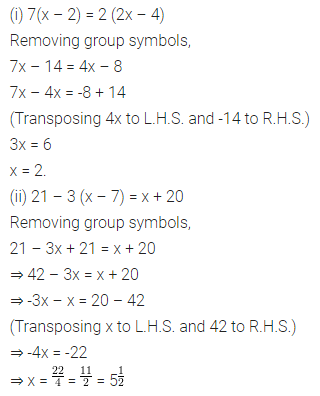
Question 4
(i)…3x –1⁄3 = 2(x – 1⁄2).+ 5
(ii)…2m⁄3 – m⁄5…= 7.
Answer-4
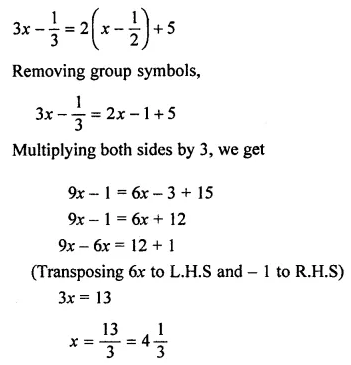
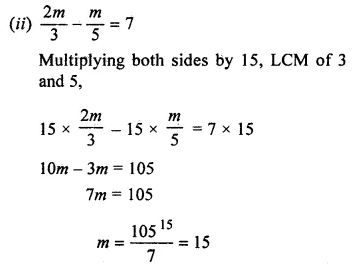
Question 5
Answer-5
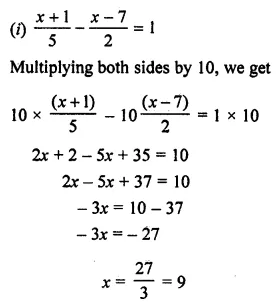
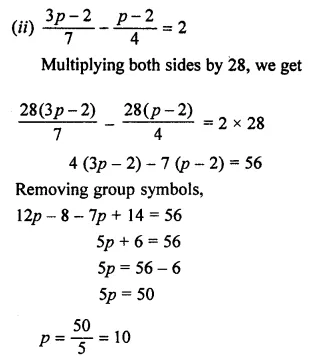
Question 6
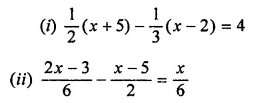
Answer-6
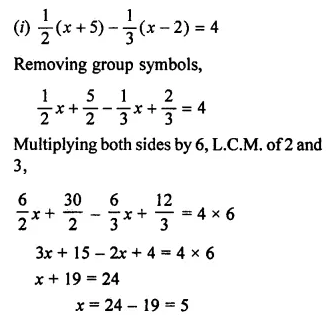

Question -7
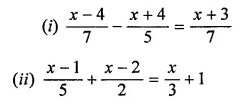
Answer-7
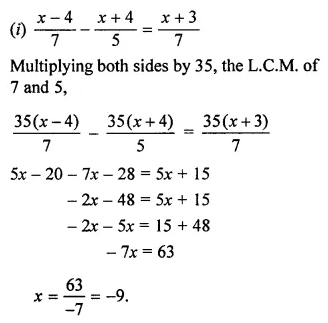

Question 8
(i) y + 1.2y = 4.4
(ii) 15% of x = 21
Answer-8
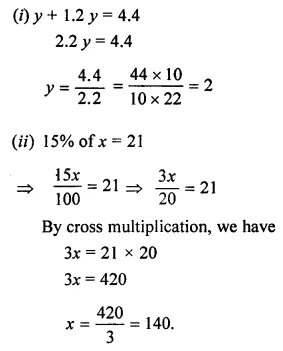
Question 9
(i) 2p + 20% of (2p – 1) = 7
(ii) 3 (2x – 1) + 25% of x = 97
Answer-9
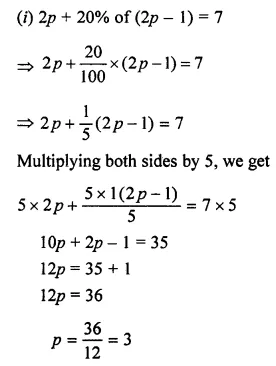
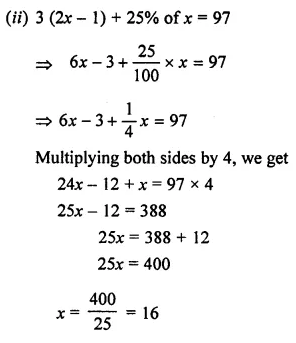
Question 10.
Find the value of p if the value of x4 – 3x3 – px – 5 is equal to 23 when x = -2.
Answer-10
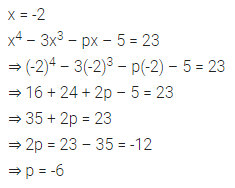
Linear Equations and Inequalities Class-7 ML Aggarwal ICSE Mathematics Solutions Exercise- 9.2
Question 1
If 7 is added to five times a number, the result is 57. Find the number.
Answer-1
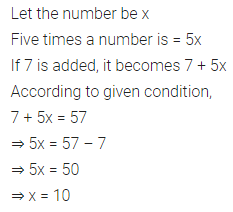
Question 2.
Find a number, such that one-fourth of the number is 3 more than 7.
Answer-2
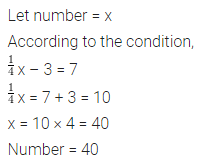
Question -3
A number is as much greater than 15 as it is less than 51. Find the number.
Answer-3
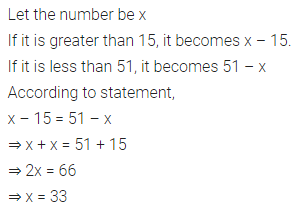
Question 4
if 1/2 is subtracted from a number and the difference is multiplied by 4, the result is 5. What is the number?
Answer-4
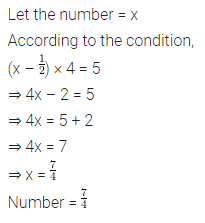
Question 5
The sum of two numbers is 80 and the greater number exceeds twice the smaller by 11. Find the numbers.
Answer
Let us assume, x and y are the two numbers and x > y
Given:
x + y = 80 ———–1
Also given:
x = 2y + 11 ————–2
Substitute the value of x from equation 1 in equation 2
2y + 11 + y = 80
3y + 11 = 80
3y = 69
y = 23
Smaller number = 23
Greater number = 2x + 11 = 2 × 23 + 11 = 46 + 11 = 57
Question 6
Find three consecutive odd natural numbers whose sum is 87
Answer-6
Let the numbers be x, x+2, x+4
A/Q x+(x+2)+(x+4) = 87
3x+6 = 87
3x = 81
x = 84/3 = 27
∴ First no. = x = 27
Second no. = x+2 = 27+2 = 29
Third no. = x+4 = 27+4 = 31
Question 7.
In a class of 35 students, the number of girls is two-fifths of the number of boys. Find the number of girls in the class.
Answer-7
Let the no. of boys in the class =x
Let the no. of girls in the class=2x/5
therefore,
x+2x/5 =35
( 5x+2x)/5=35
7x=35 x 5
7x=175
x=25
Therefore ,no. of girls =2x/5
=50/5
=10
Question 8
A chair costs ₹ 250 and the table costs ₹ 400. If a housewife purchased a certain number of chairs and two tables for ₹ 2800, find the number of chairs she purchased.
Answer-8
Let x be the number of chairs
Cost of 1 chair = Rs. 250
Cost of x chair = 250x
Cost of 1 table = Rs.400
So, cost of 2 tables = 400 x 2 = 800
We are given that a housewife purchased a certain number of chairs and two tables for Rs.2800
So,
250 x + 800 = 2800
250 x = 2800- 800
250 x = 2000
x = 2000/250
x = 8
Hence the number of chairs she purchased is 8.
Question 9
Aparna got ₹ 27840 as her monthly salary and over-time. Her salary exceeds the overtime by ₹ 16560. What is her monthly salary?
Answer-9

Question 10.
Heena has only ₹ 2 and ₹ 5 coins in her purse. If in all she has 80 coins in her purse amounting to ₹ 232, find the number of ₹ 5 coins.
Answer-10

Question 11
A purse contains ₹ 550 in notes of denominations of ₹ 10 and ₹ 50. If the number of ₹ 50 notes is one less than that of ₹ 10 notes, then find the number of ₹ 50 notes.
Answer-11

Question 12.
After 12 years, 1 shall be 3 times as old as I was 4 years ago. Find my present age.
Answer-12
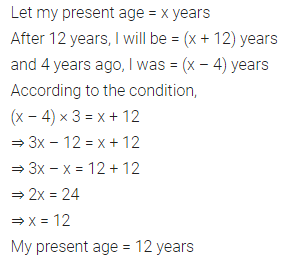
Question 13.
Two equal sides of an isosceles triangle are 3x – 1 and 2x + 2. The third side is 2x units. Find x and the perimeter of the triangle.
Answer-13
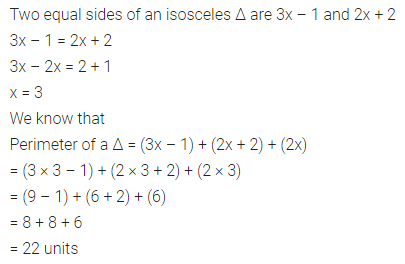
Question 14
The length of a rectangle plot is 6 m less than thrice its breadth. Find the dimensions of the plot if its perimeter is 148 m.
Answer-14

Question 15.
Two complementary angles differ by 20°. Find the measure of each angle.
Answer-15
Let one of the angles is x then other is x+20
We are given, x+x+20 = 90°
2x+20 = 90°
so, 2x = 70°
so, x =35°
so Angles are 35° and 55°
ML Aggarwal ICSE Mathematics Solutions Exercise- 9.3, Linear Equations and Inequalities Class-7
Question 1
if the replacement set is (- 5, – 3, – 1, 0, 1, 3, 4), find the solution set of:
(i) x < -2
(ii) x > 1
(iii) x ≥ -1
(iv) -5 < x < 3
(v) -3 ≤ x < 4
(vi) 0 ≤ x < 7
Answer-1
Replacement set = {-5, -3, -1, 0, 1, 3, 4}
(i) Solution set of x < – 2 = {-5, -3}
(ii) Solution set of x > 1 = {3, 4}
(iii) Solution set of x ≥ -1 = {- 1, 0, 1, 3, 4}
(iv) Solution set of -5 < x < 3 = {-3, -1, 0, 1}
(v) Solution set of -3 ≤ x < 4 = {-3, -1,0, 1, 3}
(vi) Solution set of 0 ≤ x < 7 = {0, 1, 3, 4}
Question -2
Represent the following inequations graphically:
(i) x ≤ 3, x ∈ N
(ii) x < 4, x ∈ W
(iii) -2 ≤ x < 4, x ∈ I
(iv) -3 ≤ x ≤ 2, x ∈ I
Answer-2

Question 3
Solve the following inequations.
(i) 4 – x > -2, x ∈ N
(ii) 3x + 1 ≤ 8, x ∈ W
Also represent their solutions on the number line
Answer-3

Question- 4.
Solve 3 – 4x < x – 12, x ∈ {-1, 0, 1, 2, 3, 4, 5, 6, 7}.
Answer-4

Question -5
Solve -7 < 4x + 1 ≤ 23, x ∈ I.
Answer-5

Objective Type Questions
Mental Maths, Linear Equations Class-7 ML Aggarwal ICSE Mathematics Solutions Chapter-9
Question 1
Fill in the blanks:
(i) A linear equation in one variable cannot have more than ………… solution.
(ii) If five times a number is 50, then the number is ……….
(iii) The number 4 is the ………. of the equation 2y – 5 = 3.
(iv) The equation for the statement ‘5 less than thrice a number x is 7’ is ……….
(v) …………. is a solution of the equation 4x + 9 = 5.
(vi) If 3x + 7 = 1, then the value of 5x + 13 is ………..
(vii) In natural numbers, 4x + 5 = -7 has ……….. solution.
(viii) In integers, 3x – 1 = 4 has …………. solution.
(ix) 5x + ………. = 13 has the solution -3.
(x) If a number is increased by 15, it becomes 50. Then the number is ……..
(xi) If 63 exceed another number by 21, then the other number is …………
(xii) If x ∈ W, then the solution set of x < 2 is ………..
Answer-1
(i) A linear equation in one variable
cannot have more than one solution.
(ii) If five times a number is 50, then the number is 10.
(iii) The number 4 is the solution of the equation 2y – 5 = 3.
⇒ 2y = 3 + 5 = 8
⇒ y = 4
(iv) The equation for the statement ‘5
less than thrice a number x is 7’ is 3x – 5 = 7.
Question -2
State whether the following statements are true (T) or false (F):
(i) We can add (or subtract) the same number of expression to both sides of an equation.
(ii) We can divide both sides of an equation by the same non-zero number.
(iii) 3x – 5 = 2(x + 3) + 7 is a linear equation in one variable.
(iv) The solution of the equation 3(x – 4) = 30 is x = 6.
(v) The solution of the equation 3x – 5 = 2 is x =
(vi) The solution of a linear equation in one variable is always an integer.
(vii) 4x + 5 < 65 is not an equation.
(viii) 2x + 1 = 7 and 3x – 5 = 4 have the same solution.
(ix) is a solution of the equation 5x – 1 = 8.
(x) If 5 is a solution of variable x in the equation = y, then the value of y is 18.
(xi) One-fourth of a number added to itself given 10, can be represented as + 10 = x.
Answer-2
(i) We can add (or subtract) the same number of
expression to both sides of an equation. (True)
(ii) We can divide both sides of an equation
by the same non-zero number. (True)
(iii) 3x – 5 = 2(x + 3) + 7
is a linear equation in one variable. (True)
3x – 5 = 2x + 6 + 7
⇒ 3x – 2x = 6 + 7 + 5
⇒ x = 18
(iv) The solution of the equation
3(x – 4) = 30 is x = 6. (False)
Correct:
3(x – 4) = 30
⇒ x – 4 = 10
Multiple Choice Question (MCQ)
ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 9 Linear Equations and Inequalities
Question 3
Which of the following is not a linear equation in one variable?
(a) 3x – 1 = 7
(b) 5y – 2 = 3 (y + 2)
(c) 2x – 3 =
(d) 7p + q = 3
Answer-3
7p + q = 3 is not a linear equation in one variable?
Question 4.
The solution of the equation 1⁄3 (2y – 1) = 3 is
(a) 5
(b) 3
(c) 2
(d) 1
Answer-4
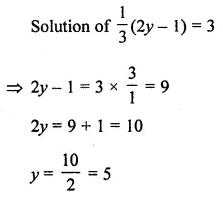
Question- 5
x = -1 is a solution of the equation
(a) x – 5 = 6
(b) 2x + 5 = 7
(c) 2(x – 2) + 6 = 0
(d) 3x + 5 = 4
Answer-5
by guess put x= -1 in (b) to get RHS
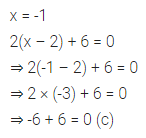
Question 6.
If 3(3n – 10) = 2n + 5, then the value of n is
(a) 12
(b) 5
(c) 3
(d) -5
Answer-6
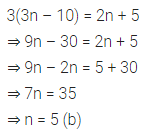
Question -7.
-1 is not a solution of the equation
(a) x + 1 = 0
(b) 3x + 4 = 1
(c) 5x + 7 = 2
(d) x – 1 = 2
Answer-7
by guess put x= -1 in (d) to not get RHS
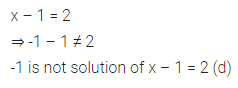
Question 8.
The value of p for which the expressions p – 13 and 2p + 1 become equal is
(a) 0
(b) 14
(c) -14
(d) 5
Answer-8
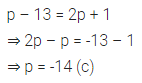
Question 9.
The equation which cannot be solved in integers is
(a) 5x – 3 = -18
(b) 3y – 5 = y – 1
(c) 3p + 8 = 3 + p
(d) 9z + 8 = 4z – 7
Answer-9
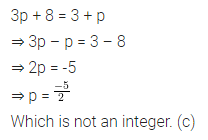
Question 10.
The solution of which of the following equations is neither an integer nor a fraction?
(a) 2x + 5 = 1
(b) 3x – 7 = 0
(c) 5x – 7 = x + 1
(d) 4x + 7 = x + 2
Answer-10
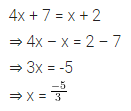
Question -11
If the sum of two consecutive even numbers is 54, then the smaller number is
(a) 25
(b) 26
(c) 27
(d) 28
Answer-11
Let first even integer = 2x
Then second integer = 2x + 2
2x + 2x + 2 = 54
⇒ 4x = 54 – 2
⇒ 4x = 52
⇒ x = 13
Smaller even integer = 2 × 13 = 26 (b)
Question- 12.
If the sum of two consecutive odd numbers is 28, then the bigger number is
(a) 19
(b) 17
(c) 15
(d) 13
Answer-12
Let first odd number = x
Then second = x + 2
x + x + 2 = 28
⇒ 2x = 28 – 2 = 26
⇒ x = 13
Bigger odd number = 13 + 2 = 15 (c)
Question-13
If 5 added to thrice an integer is -7, then the integer is
(a) -6
(b) -5
(c) -4
(d) 4
answer-13
Let integer be x, then 3x + 5 = -7
⇒ 3x = -7 – 5
⇒ 3x = -12
⇒ 3x= -14
⇒ x = -4 (c)
Question-14
If the length of a rectangle is twice its breadth and its perimeter is 120 m, then its length is
(a) 20 m
(b) 30 m
(c) 40 m
(d) 60 m
Answer-14
Let breadth of a rectangle = x
Then length = 2x
Perimeter = 2(x + 2x) = 2 × 3x = 6x
6x = 120
⇒ x = 20
Length = 2x = 20 × 2 = 40 m (c)
Question 15.
If the difference of two complementary angles is 10°, then the smaller angle is
(a) 40°
(b) 50°
(c) 45°
(d) 35°
Answer-15
Let first angle = x
Then its complementary angle = 90° – x
Now x – (90° – x) = 10°
⇒ x – 90° + x = 10°
⇒ 2x = 10° + 90° = 100°
⇒ x = 50°
Second angle = 90° – 50° = 40°
Smaller angle = 40° (a)
Question- 16.
If the difference of two supplementary angles is 30°, then the larger angle is
(a) 60°
(b) 75°
(c) 90°
(d) 105°
Answer-16
Let first supplementary angle = x
Then second = 180° – x
x – (180° – x) = 30°
⇒ x – 180° + x = 30°
⇒ 2x = 30° + 180° = 210°
⇒ x = 105°
Larger angle = 105° (d)
Question -17.
(a) {-2, -1,0, 1, 2}
(b) {-1, 0, 1, 2, 3}
(c) {0, 1, 2, 3}
(d) (0, 1, 2}
x ∈ W
Solution set -2 ≤ x < 3 = {-2, -1, 0, 1, 2} (a)
Value Based Questions
ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 9 Linear Equations and Inequalities
Question 1
On his 13th birthday, a boy decided to distribute blankets to the poor people instead of giving a party to his friends. Half of the blankets he distributed in an old age home, three fourths of the remaining in an orphanage and rest 20 were distributed to the roadside beggars. Find the number of blankets he had. What values are being promoted
Answer-1
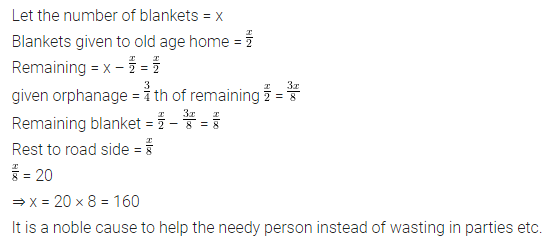
Higher Order Thinking Skills ( HOTS )
ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 9 Linear Equations and Inequalities
Question 1.
Two persons start moving from two points A and B in opposite directions towards each other. One person start moving from A at a speed of 4 km/h and meets the other person coming from B after 6 hours. If the distance between A and B is 42 km, find the speed of the other person.
Answer-1
Distance between A and B = 42 km
Speed of one person = 4 km/h
After 6 hours they meet together
Let speed of other person = x km/h
According to the condition,
4 × 6 + x × 6 = 42
⇒ 24 + 6x = 42
⇒ 6x = 42 – 24 = 18
⇒ x = 3
Speed of other person = 3 km/h
Question 2.
There are some benches in the classroom. If 4 students sit on each bench then 3 benches remain empty and if 3 students sit on each bench then 3 students remain standing. Find the number of students in the class.
Answer-2
Let number of benches in a classroom = x
According to the condition,
No. of students = (x – 3) × 4 and x × 3 + 3
(x – 3) × 4 = x × 3 + 3
⇒ 4x – 12 = 3x + 3
⇒ 4x – 3x = 3 + 12
⇒ x = 15
Number of benches = 15
and number of students = 15 × 3 + 3 = 45 + 3 = 48
Check Your Progress
ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 9 Linear Equations and Inequalities
Question 1.
Solve the following equations :
(i) 2 (x – 5) + 3 (x – 2) = 8 + 7 (x – 4)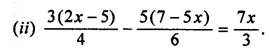
Answer-2
(i) 2 (x – 5) + 3 (x – 2) = 8 + 7 (x – 4)
Removing group symbols,
2x – 10 + 3x – 6 = 8 + 7x – 28
⇒ 5x- 16 = 7x – 20
⇒ 5x – 7x = – 20 + 16
(Transposing -16 to R.H.S and 7x to L.H.S)
⇒ -2x = -4
⇒ -x = -4/2
⇒ x = 2
(ii)
Solve your self by taking LCM of 4, 6
then cross multiply
find x
Question 2
A number exceeds its three-fifth by 22. Find the number.
Answer-2
Let number be x..
Given, number exceeds its 3⁄5 by 22..so
= x – 3x⁄5 = 22
⇒ 2x/5 =22
⇒ 2x=110
⇒x=55
Question 3
When 9 is added to twice a number, the result is 3 more than thrice the number. Find the number.
Answer
Let the number be x
Twice a number = 2x
Thrice a number = 3x
According to statement,
9 + 2x = 3 + 3x
⇒ 9 – 3 = 3x – 2x
⇒ 6 = x
⇒ x = 6
Question 4
The ten’s digit of a two digit number is twice the unit’s digit. The sum of the number and its unit’s digit is 66. Find the number.
Answer-4
Let the unit’s digit be x.
Ten’s digit = 2x.
The number =10 × 2x + x = 20x + x
According to statement,
10 × 2x + x + x = 66
⇒ 20x + x + x = 66
⇒ 22x = 66
⇒ x = 3
The number = 20x + x = 20 × 3 + 3 = 60 + 3 = 63
Question 5
A student bought some pens at ₹ 8 each and some pencils at ₹ 1.50 each. If the total number of pens and pencils purchased is 16 and their total cost is ₹ 50, how many pens did he buy?
Answer-5
The total number of pens and pencils purchased = 16
Let the number of pens bought = x
The number of pencils bought = 16 – x
Cost of pens bought = 8x
Cost of pencils bought = 1.50 (16 – x)
According to given condition,
8x + 1.50 (16 – x) = ₹ 50
⇒ 8x + 24 – 1.50x = 50
⇒ 6.50x = 50 – 24
Question 6
Arvind is eight years older than his sister. In three years, he will be twice as old as his sister. How old are they now?
Answer-6
Let the sister’s age = x years
Arvind’s age = (x + 8) years.
In three years, sister’s age = (x + 3) years
In three years, Arvind’s age = (x + 8 + 3) years
According to statement,
x + 8 + 3 = 2(x + 3)
⇒ x + 11 = 2x + 6
⇒ x – 2x = 6 – 11
⇒ -x = -5
⇒ x = 5.
Sister’s age = 5 years
Arvind’s age = 5 + 8 = 13 years.
Question -7
The angles of a triangle are in the ratio 1 : 2 : 3. Find their measure in degrees.
Answer-7
Let the angles of a Δ are x, 2x and 3x.
We know that
Sum of ∠s of a Δ is 180°
x + 2x + 3x = 180°
⇒ 6x = 180°
⇒ x = 30°
∠s of a Δ are
1x = 1 × 30° = 30°,
2x = 2 × 30° = 60°,
and 3x = 3 × 30° = 90°
Question 8.
Solve the following in equations and represent their solution on a number line:
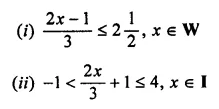
Answer-8
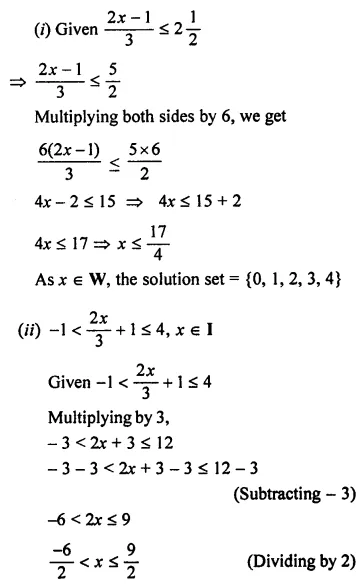

— End of Linear Equations Class-7 ML Aggarwal Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -7
Thanks