Linear Inequation MCQ Type Questions Class-10 ICSE Maths for Sem-1. These MCQ / Objective Type Questions of Linear Inequation is based on latest reduced syllabus according 2021-22 session on bifurcated pattern. Main motto of MCQ Type Question is cracking the next upcoming exam of council. Visit official website CISCE for detail information about ICSE Board Class-10 Maths
MCQ Type Questions of Linear Inequation for ICSE Class-10
| Board | ICSE |
| Class | 10th ( x ) |
| Subject | Maths |
| Chapter | Linear Inequation |
| Syllabus | on bifurcated syllabus (after reduction) |
| bifurcated pattern |
Semester-1 |
| Session | 2021-22 |
| Topic | MCQ / Objective Type Question |
ICSE Maths Linear Inequation MCQ Type Questions
Question 1 Find the largest value of x for which 2(x – 1) 9 – x and x ∈W.
(a) 1
(b) 2
(c) 3
(d) 0
Answer- (c) 3
Question 5 3 – 2x ≥ x – 12 given that x N. the solutions set of x is
(a) {1, 2, 3, 4, -5}
(b) {- 1, 2, 3, 4, 5}
(c) {1, – 2, 3, 4, 5}
(d) {1, 2, 3, 4, 5}
Answer- (d) {1, 2, 3, 4, 5}
Hint
3 – 2x x – 12
-2x – x -12 – 3
-3x -15
x 5
Since, x N, therefore,
Solution set = {1, 2, 3, 4, 5}
Question 6 Solution set of the inequation, 3x – 11 < 3 where x ∈ {1, 2, 3, ……, 10}.is
(a) {-1, 2, 3, 4,}
(b) {1, -2, 3, 4,}
(c) {1, 2, -3, 4,}
(d) {1, 2, 3, 4,}
Answer- (d) {1, 2, 3, 4, }
Hint
Given inequation, 3x – 11 < 3
3x < 3 + 11
3x < 14
⇒ x < 14/3
But, x ∈ {1, 2, 3,……, 10}
Hence, the solution set is {1, 2, 3, 4}.
Question 7 If x is a negative integer, find the solution set of 2/3 + 1/3 (x + 1) > 0.
(a) {-1, -2}.
(b) {-2, -3}.
(c) {-3, -4}.
(d) {-4, -5}.
Answer-(a) {-1, -2}.
Hint
Given inequation, 2/3 + 1/3 (x + 1) > 0.
2/3 + x/3 + 1/3 > 0
x/3 + 1 > 0
x/3 > -1
⇒ x > -3
As x is a negative integer
The solution set is {-1, -2}.
Question 8 Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9} solution set will be x – 3 < 2x – 1.
(a) {, 2, 3, 4, 5, 6, 7, 9}
(b) {1, 2, 3, 4, 5, 6, 7, 9}
(c) {1, 2, 3, 4, 5, 6, 7, }
(d) {1, 2, 3, 5, 6, 7, 9}
Answer-(b) {1, 2, 3, 4, 5, 6, 7, 9}
Hint
Given inequation, x – 3 < 2x – 1
x – 2x < – 1 + 3
-x < 2
⇒ x > -2
But, x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Hence, the solution set is {1, 2, 3, 4, 5, 6, 7, 9}
Question 9 In following inequation the solution set are
-2 + 10x ≤ 13x + 10 ≤ 24 + 10x, x ∈ Z
(a) {, -1, 0, 1, }
(b){ -2, -1, 0, 1, 2, }
(c){-4, -3, -2, -1, 0, 1, 2, 3, 4}
(d) { -3, -2, -1, 0, 1, 2, 3, }
Answer-(c){-4, -3, -2, -1, 0, 1, 2, 3, 4}
Hint
Given inequation, -2 + 10x ≤ 13x + 10 ≤ 24 + 10x
So, we have
-2 + 10x ≤ 13x + 10 and 13x + 10 ≤ 24 + 10x
10x – 13x ≤ 10 + 2 and 13x – 10x ≤ 24 – 10
-3x ≤ 12 and 3x ≤ 14
x ≥ -12/3 and x ≤ 14/3
x ≥ -4 and x ≤ 14/3
So, -4 ≤ x ≤ 14/3
As x ∈ Z
Thus, the solution set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}
Question 10 . If x ∈ I, A is the solution set of 2 (x – 1) < 3x – 1 and B is the solution set of 4x – 3 ≤ 8 + x, set of A ∩ B.
(a) {0, 1, 2, 3, …)
(b) {0, 1, 2, 3)
(c) {4,5,6,…. )
(d) {3, 2, 1, 0, -1, …)
Answer- {0, 1, 2, 3)
Hint
Given inequations,
2 (x – 1) < 3x – 1 and 4x – 3 ≤ 8 + x for x ∈ I
Solving for both, we have
2x – 3x < 2 – 1 and 4x – x ≤ 8 + 3
-x < 1 and 3x ≤ 11
x > -1 and x ≤ 11/3
Hence,
Solution set A = {0, 1, 2, 3, …}
Solution set B = {3, 2, 1, 0, -1, … }
Thus, A ⋂ B = {0, 1, 2, 3)
Question 11 A = {x : 11x – 5 > 7x + 3, x ∈ R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈ R} the range of set A ∩ B is
(a) x < 4
(b)x < 4
(c) x ≤ 4
(d) x ≥ 4
Answer- (d) x ≥ 4
Hint
Given, A = {x : 11x – 5 > 7x + 3, x ∈ R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈ R}
Solving for A,
11x – 5 > 7x + 3
11x – 7x > 3 + 5
4x > 8
x > 2
Hence, A = {x : x > 2, x ∈ R}
Next, solving for B
18x – 9 ≥ 15 + 12x
18x – 12x ≥ 15 + 9
6x ≥ 24
x ≥ 4
Hence, B = {x : x ≥ 4, x ∈ R}
Thus, A ∩ B = x ≥ 4
Question 12 Given 20 – 5 x < 5 (x + 8), the smallest value of x, when (i) x ∈ I, (ii) x ∈ W, (iii) x ∈ N.
(a) {2,),(3) ,(4 )
(b)x {-2),(-1),( 0)
(c) x {-1), (0), (1,)
(d) x {1), (2,) (3,)
Answer- (c) x {-1), (0), (1,)
Hint
Given inequation, 20 – 5 x < 5 (x + 8)
20 – 5x < 5x + 40
-5x – 5x < 40 – 20
-10x < 20
-x < 20/10
x > -2
Thus,
(i) For x ∈ I, the smallest value = -1
(ii) For x ∈ W, the smallest value = 0
(iii) For x ∈ N, the smallest value = 1
Question -13 the solution set of
if x ∈ N
(a){1, 2, 3, 4, 5, .. , 13}
(b){, 2, 3, 4, 5, .. , 13}
(c) {, 3, 4, 5, .. , 13}
(d){, 4, 5, .. , 13}
Answer- (a) {1, 2, 3, 4, 5, .. , 13}
Hint
=> 88 – 16x ≥ 45 – 15x + 30
(L.C.M. of 8, 5, 4 = 40}
=> – 16x + 15x ≥ 45 + 30 – 88
=> – x ≥ – 13
=>x ≤ 13
x ≤ N.
Solution set = {1, 2, 3, 4, 5, .. , 13} Ans.
Question -14 the values of x, which satisfy the inequation :
![]()
, x ∈ N.
(a) 15/4 ≥ x ≥ – 5
(b)15/4 ≥ x ≥ – 4
(c) 15/4 ≥ x ≥ – 3
(d) 15/4 ≥ x ≥ – 2
Answer-(d) 15/4 ≥ x ≥ – 2
Hint
![]() , x ∈ N
, x ∈ N
⇒ – 2 – 1/2 ≤ 1/2 – 2x/3 – 1/2 ≤ 11/6 – 1/2
[By subtracting 1/2 on both sides of inequality]
⇒ – 5/2 ≤ 2x/3 ≤ 8/6
⇒ – 15 ≤ – 4x ≤ 8
⇒ 15 ≥ 4x ≥ – 8
⇒ 15/4 ≥ x ≥ – 2
Question- 15 The greatest integer which is such that if 7 is added to its double, the resulting number becomes greater than three times the integer
(a) greatest = 6
(b) greatest = 5
(c) greatest =4
(d) greatest = 3
Answer -(a) greatest = 6
Hint Let the greatest integer = x
According to the condition,
2x + 7 > 3x
⇒ 2x – 3x > – 7
⇒ – x > – 7
⇒ x < 7
Value of x which is greatest = 6 Ans.
Question -16 One-third of a bamboo pole is buried in mud, one-sixth of it is in water and the part above the water is greater than or equal to 3 metres. Find the length of the shortest pole.
(a) shortest in length 4 metres
(b) shortest in length5 metres
(c) shortest in length 6 metres
(d) shortest in length 7 metres
Answer- (c) shortest in length 6 metres
Hint Length of pole which is buried in mud = x/3
Length of pole which is in the water = x/6
According to this problem,
x – [x/3 + x/6] ≥ 3
⇒ x – (2x + x)/6 ≥ 3
⇒ x – x/2 ≥ 3
⇒ x/2 ≥ 3
⇒ x ≥ 6
∴ Length of pole (shortest in length) = 6 metres
Question- 17 If x ∈ { – 3, – 1, 0, 1, 3, 5}, then the solution set of the inequation 3x – 2 ≤ 8 is
(a) { – 3, – 1, 1, 3}
(b) { – 3, – 1, 0, 1, 3}
(c) { – 3, – 2, – 1, 0, 1, 2, 3}
(d) { – 3, – 2, – 1, 0, 1, 2}
Solution set = (b) { -3, -1, 0, 1, 3}
Hint x ∈ { -3, -1, 0, 1, 3, 5}
3x – 2 ≤ 8
….⇒ 3x ≤ 8 + 2
and ⇒ 3x ≤ 10
so ⇒ x ≤ 10/3
therefore ⇒ x < 10/3
Solution set = { -3, -1, 0, 1, 3}
Question -18 If x ∈ W, then the solution set of the inequation 3x + 11 ≥ x + 8 is
(a) { – 2, – 1, 0, 1, 2, …}
(b) { – 1, 0, 1, 2, …}
(c) {0, 1, 2, 3, …}
(d) {x : x∈R,x≥-3/2}
Answer -(c) {0, 1, 2, 3, …}
Hint x ∈ W
3x + 11 ≥ x + 8
⇒ 3x – x ≥ 8 – 11
⇒ 2x ≥ – 3
⇒ x ≥ -3/2
⇒ x ≥ -1.1/2
Solution set = {0, 1, 2, 3,…..}
Question -19 If x ∈ W, then the solution set of the inequation 5 – 4x ≤ 2 – 3x is
(a) {…, – 2, – 1, 0, 1, 2, 3}
(b) {1, 2, 3}
(c) {0, 1, 2, 3}
(d) {x : x ∈ R, x ≤ 3}
Answer -(c) {0, 1, 2, 3}
Hint x ∈ W
5 – 4x < 2 – 3x
⇒ 5 – 2 ≤ 3x + 4x
⇒ 3 ≤ x
Solution set = {0, 1, 2, 3,} (c)
Question -20 If x ∈ I, then the solution set of the inequation 1 < 3x + 5 ≤ 11 is
(a) { – 1, 0, 1, 2}
(b) { – 2, – 1, 0, 1}
(c) { – 1, 0, 1}
(d) {x : x ∈ R, -4/3 < x ≤ 2}
Answer- (a) { – 1, 0, 1, 2}
Hint
x ∈ I
1 < 3x + 5 ≤ 11
⇒ 1 < 3x + 5
⇒ 1 – 5 < 3x
⇒ – 4 < 3x
⇒ -4/3 < x
And 3x + 5 ≤ 11 ⇒ 3x ≤ 11 – 5
⇒ 3x ≤ 6
⇒ x ≤ 6/3
⇒ x ≤ 2
∴ -4/3 < x ≤ 2
Solution set = {- 1, 0, 1, 2}
Question -21 If x ∈ R, the solution set of 6 ≤ – 3 (2x – 4) < 12 is
(a) {x : x ∈ R, 0 < x ≤ 1}
(b) {x : x ∈ R, 0 ≤ x < 1}
(c) {0, 1}
(d) none of these
Answer- (a) {x : x ∈ R, 0 < x ≤ 1}
Hint x ∈ R
6 ≤ – 3(2x – 4) < 12
⇒ 6 ≤ – 3(2x – 4)
⇒ 6 ≤ – 6x + 12
⇒ 6x ≤ 12 – 6
⇒ 6x ≤ 6
⇒ x ≤ 6/6
⇒ x ≤ 1
And -3(2x – 4) < 12
⇒ – 6x + 12 < 12
⇒ – 6x < 0
⇒ x < 0 ………(ii)
From (i) and (iii),
∴ 0 < x ≤ 1
Solution set = {x : x ∈ R, 0 < x ≤ 1}
Question -22 Find three smallest consecutive natural numbers such that the difference between one-third of the largest and one-fifth of the smallest is at least 3.
(a) {18, 19, 20}
(b) {17, 18, 19}
(c) {16, 17, 18}
(d) none of these
Answer- (a) {18, 19, 20}
Hint
Let first least natural number = x
then second number = x + 1
and third number = x + 2
According to the condition 1/3(x + 2) – 1/5 (x) ≥ 3
5x + 10 – 3x ≥ 45
(Multiplying by 15 the L.C.M. of 2 and 5)
2x ≥ 45 – 10
⇒ 2x ≥ 35
x ≥ 35/2
⇒ x ≥ 17.1/2
∵ x is a natural least number
∴ x = 18
∴ find least natural number = 18
Second number = 18 + 1 = 19
And third numbers = 18 + 2 = 20
Hence, least natural numbers are 18, 19, 20
–: End of Linear Inequation MCQ Type Questions Class-10 ICSE Maths :-
-: also visit :-
ICSE MCQs for Class-10 Subject-Wise / Chapter-Wise
ICSE Class-10 Text book Solutions, Notes , Syllabus, Paper, Notes
Please share with your ICSE friends if it is helpful
Thanks
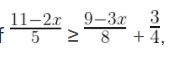



pls check your question no 1 in mcq of linear in equqtion
ok
In question number 8, the answer is marked as (b) but there is no 8 in the solution set