
Linear Programming MCQs Type Questions with Answer for ISC Class 12 Maths . These MCQs / Objective Type Questions is based on latest reduced syllabus according 2021-22 session on bifurcated pattern. Main motto of MCQ Type Question is cracking the next upcoming Sem-2 exam of council. Visit official website CISCE for detail information about ISC Class-12 Maths.
ISC Class 12 Linear Programming MCQs Type Questions with Answer
| Board | ISC |
| Class | 12th (XII) |
| Subject | Maths |
| Chapter | Linear Programming |
| Syllabus | on bifurcated syllabus (after reduction) |
| Session | 2021-22 |
| Bifurcated | Sem-2 |
| Topic | MCQs / Objective Type Question |
ISC Linear Programming MCQs Questions with Answers for Class-12 Maths
Question 1: Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
(a) 20 at (1, 0)
(b) 30 at (0, 6)
(c) 37 at (4, 5)
(d) 33 at (6, 3)
Answer: (c) 37 at (4, 5)
Question 2: Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
(a) 16 at (4, 0)
(b) 24 at (0, 4)
(c) 24 at (6, 0)
(d) 36 at (0, 6)
Answer: (d) 36 at (0, 6)
Question3: Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
(a) 12 at (2, 0)
(b) 140/3 at (2/3, 1/3)
(c) 16 at (2, 1)
(d) 4 at (0, 1)
Answer: (c) 16 at (2, 1)
Question 4: Maximize Z = 10×1 + 25×2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
(a) 80 at (3, 2)
(b) 75 at (0, 3)
(c) 30 at (3, 0)
(d) 95 at (2, 3)
Answer: (d) 95 at (2, 3)
Question 5: In maximization problem, optimal solution occurring at corner point yields the
(a) highest value of z
(b) lowest value of z
(c) mid values of z
(d) mean values of z
Answer : (a) highest value of z
Question 6: In a LPP, the objective function is always
(a) Linear
(b) Quadratic
(c) Cubic
(d) Biquadratic
Answer : (a) Linear
Question 7: A feasible solution to a linear programming problem
(a) Must satisfy all of the problem’s constraints simultaneously
(b) Need not satisfy all of the constraints, only the non-negativity constraints
(c) Must be a corner point of the feasible region
(d) Must give the maximum possible profit
Answer : (a) Must satisfy all of the problem’s constraints simultaneously
Question 7: The corner points of the bounded feasible region of a LPP are A(0,50), B(20, 40), C(50, 100) and D(0, 200) and the objective function is Z = x + 2y. Then the maximum value is
(a) 400
(b) 250
(c) 450
(d) 100
Answer : (a) 400
Question 8: The feasible region (shaded) for a L.P.P is shown in the figure. The maximum Z = 5x + 7y is
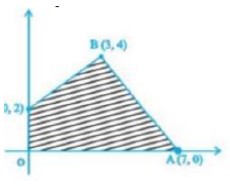
(a) 43
(b) 47
(c) 45
(d) 49
Answer : (a) 43
Question 9: The minimum value of Z = 4x + 3y subjected to the constraints 3x + 2y ≥ 160, 5 + 2y ≥ 200, 2y ≥ 80; x, y ≥ 0 is
(a) 220
(b) 300
(c) 230
(d) none of these
Answer: (a) 220
Question 10: The maximum value of Z = 3x + 2y, subjected to x + 2y ≤ 2, x + 2y ≥ 8; x, y ≥ 0 is
(a) 32
(b) 24
(c) 40
(d) none of these
Answer: (d) none of these
Question 11: Maximize Z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x ≥ 0, y ≥ 0.
(a) 44 at (4, 2)
(b) 60 at (4, 2)
(c) 62 at (4, 0)
(d) 48 at (4, 2)
Answer: (b) 60 at (4, 2)
Question 12: In solving the LPP:
“minimize f = 6x + 10y subject to constraints x ≥ 6, y ≥ 2, 2x + y ≥ 10, x ≥ 0, y ≥ 0” redundant constraints are
(a) x ≥ 6, y ≥ 2
(b) 2x + y ≥ 10, x ≥ 0, y ≥ 0
(c) x ≥ 6
(d) none of these
Answer: (b) 2x + y ≥ 10, x ≥ 0, y ≥ 0
Question 13: Region represented by x ≥ 0, y ≥ 0 is
(a) first quadrant
(b) second quadrant
(c) third quadrant
(d) fourth quadrant
Answer: (a) first quadrant
Question 14: The region represented by the inequalities
x ≥ 6, y ≥ 2, 2x + y ≤ 0, x ≥ 0, y ≥ 0 is
(a) unbounded
(b) a polygon
(c) exterior of a triangle
(d) None of these
Answer: (d) None of these
Question 15: Objective function of a L.P.P.is
(a) a constant
(b) a function to be optimised
(c) a relation between the variables
(d) none of these
Answer: (b) a function to be optimised
Question 16: The optimal value of the objective function is attained at the points
(a) on X-axis
(b) on Y-axis
(c) which are comer points of the feascible region
(d) none of these
Answer: (c) which are comer points of the feascible region
Question 17: Z = 4x1 + 5x2, subject to 2x1 + x2 ≥ 7, 2x1 + 3x2 ≤ 15, x2 ≤ 3, x1, x2 ≥ 0. The minimum value of Z occurs at
(a) (3.5, 0)
(b) (3, 3)
(c) (7.5, 0)
(d) (2, 3)
Answer: (a) (3.5, 0)
Question 18: The maximum value of f = 4x + 3y subject to constraints x ≥ 0, y ≥ 0, 2x + 3y ≤ 18; x + y ≥ 10 is
(a) 35
(b) 36
(c) 34
(d) none of these
Answer: (d) none of these
Question 19: Minimize Z = 20x1 + 9x2, subject to x1 ≥ 0, x2 ≥ 0, 2x1 + 2x2 ≥ 36, 6x1 + x2 ≥ 60.
(a) 360 at (18, 0)
(b) 336 at (6, 4)
(c) 540 at (0, 60)
(d) 0 at (0, 0)
Answer: (b) 336 at (6, 4)
Question 20: Z = 8x + 10y, subject to 2x + y ≥ 1, 2x + 3y ≥ 15, y ≥ 2, x ≥ 0, y ≥ 0. The minimum value of Z occurs at
(a) (4.5, 2)
(b) (1.5, 4)
(c) (0, 7)
(d) (7, 0)
Answer: (b) (1.5, 4)
Question 21: Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at
(a) (8, 0)
(b) (5/2,15/4)
(c) (7/2,9/4)
(d) (0, 10)
Answer: (c) (7/2,9/4)
Question 22: Z = 7x + y, subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at
(a) (3, 0)
(b) (1/2,5/2)
(c) (7, 0)
(d) (0, 5)
Answer: (d) (0, 5)
Question 22: In equation 3x – y ≥ 3 and 4x – 4y > 4
(a) Have solution for positive x and y
(b) Have no solution for positive x and y
(c) Have solution for all x
(d) Have solution for all y
Answer: (a) Have solution for positive x and y
Question 23: The maximum value of Z = 4x + 2y subject to the constraints 2x + 3y ≤ 18, x + y ≥ 10, x, y ≤ 0 is
(a) 36
(b) 40
(c) 30
(d) None of these
Answer: (d) None of these
Question 24: Of all the points of the feasible region for maximum or minimum of objective function the points
(a) Inside the feasible region
(b) At the boundary line of the feasible region
(c) Vertex point of the boundary of the feasible region
(d) None of these
Answer: (c) Vertex point of the boundary of the feasible region
Question 25: The objective function Z = 4x + 3y can be maximised subjected to the constraints 3x + 4y ≤ 24,8x + 6y ≤ 48, x ≤ 5, y ≤ 6; x, y ≥ 0
(a) at only one point
(b) at two points only
(c) at an infinite number of points
(d) none of these
Answer: (c) at an infinite number of points
Question 25: If the constraints in a linear programming problem are changed
(a) solution is not defined
(b) the objective function has to be modified
(c) the problems is to be re-evaluated
(d) none of these
Answer: (c) the problems is to be re-evaluated
Question 26: Corner points of the feasible region determined by the system of linear constraints are (0, 3),
(1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
(a) p = 2q
(b) p = q/2
(c) p = 3q
(d) p = q
Answer: (b) p = q/2
Question 27: The optimal value of the objective function is attained at the points
(a) given by intersection of inequation with y-axis only.
(b) given by intersection of inequation with x-axis only.
(c) given by corner points of the feasible region.
(d) none of these
Answer: (c) given by corner points of the feasible region.
Question 28: The solution set of the inequation 3x + 2y > 3 is
(a) half plane not containing the origin
(b) half plane containing the origin
(c) the point being on the line 3x + 2y = 3
(d) None of these
Answer: (a) half plane not containing the origin
Question 29: In an LPP, if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then the number of points of which Zmax occurs is
(a) 0
(b) 2
(c) finite
(d) infinite
Answer: (d) infinite
Question 30: Which of the following statement is correct?
(a) Every LPP admits an optimal solution.
(b) Every LPP admits unique optimal solution.
(c) If a LPP gives two optimal solutions it has infinite number of solutions.
(d) None of these
Answer: (b) Every LPP admits unique optimal solution.
Question 31: The corner point of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
(a) The quantity in column A is greater
(b) The quantity in column B is greater
(c) The two quantities are equal
(d) The relationship cannot be determined On the basis of the information supplied
Answer: (b) The quantity in column B is greater
Question 32: Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at
(a) (4, 0)
(b) (28, 8)
(c) (2, 7/2)
(d) (0, 3)
Answer: (c) (2, 7/2)
Question 33: Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
(a) 59 at (9/2, 5/2)
(b) 42 at (6, 0)
(c) 49 at (7, 0)
(d) 57.2 at (0, 5.2)
Answer: (a) 59 at (9/2, 5/2)
Question 34: The maximum value of Z = 3x + 4y subjected to contraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0 and y ≥ 0 is
(a) 120
(b) 140
(c) 100
(d) 160
Answer: (b) 140
Question 35: Feasible region in the set of points which satisfy
(a) The objective functions
(b) Some the given constraints
(c) All of the given constraints
(d) None of these
Answer: (c) All of the given constraints
–: End of Linear Programming MCQs Type Questions :–
-: also visit :-
- ISC Sem-2 Question Bank Class-12
- Sem-2 ISC Specimen Paper for Class-12
- ISC Class-12 Textbook Solutions ,Syllabus, Solved Paper
- Previous Year Question Paper for ISC Class-12
Please share with your ISC friends if it is helpful
Thanks


