Lines and Angles Class-7 ML Aggarwal ICSE Mathematics Solutions Chapter-10. We provide step by step Solutions of Exercise / lesson-10 Lines and Angles ICSE Class-7th ML Aggarwal Maths.
Our Solutions contain all type Questions with Exe-10.1 , Exe-10.2, Objective Type Questions ( including Mental Maths Multiple Choice Questions , HOTS) and Check Your Progress to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7 Mathematics.
Lines and Angles Class-7 ML Aggarwal ICSE Mathematics Solutions Chapter-10
–: Select Topic :–
Objective Type Questions, Mental Maths,
Multiple Choice Questions ,(MCQ)
Exercise-10.1, Lines and Angles Class-7 ML Aggarwal ICSE Mathematics Solutions
Question 1
(i) Can two right angles be complementary?
(ii) Can two right angles be supplementary?
(iii) Can two adjacent angles be complementary?
(iv) Can two adjacent angles be supplementary?
(v) Can two obtuse angles be adjacent?
(vi) Can an acute angle be adjacent to an obtuse angle?
(vii) Can two right angles form a linear pair?
Answer
(i) No, as the sum of two complementary angles is 90°.
(ii) Yes.
(iii) Yes.
(iv) Yes.
(v) Yes.
(vi) Yes.
(vii) Yes.
Question 2
Find the complement of each of the following angles:
Answer
(i) Complement of 25° = 90° – 25° = 65°
(ii) Complement of 63° = 90° – 63° = 27°
(iii) Complement of 57° = 90° – 57° = 33°
Question 3.
Find the supplement of each of the following angles:
Answer
(i) Supplement of 105° is 180° – 105° = 75°
(ii) Supplement of 875° is 180° – 87° = 93°
(iii) Supplement of 142° is 180° – 142° = 38°
Question 4
Identify which of the following pairs of angles are complementary and which are supplementary:
(i) 55°, 125°
(ii) 34°, 56°
(iii) 137°, 43°
(iv) 112°, 68°
(v) 45°, 45°
(vi) 72°, 18°
Answer
(i) 55°, 125° are supplementary.
(ii) 34°, 56° are complementary.
(iii) 137°, 43° are supplementary.
(iv) 112°, 68° are supplementary.
(v) 45°, 45° are complementary.
(vi) 12°, 18° are complementary.
Question 5
(i) Find the angle which is equal to its complement.
(ii) Find the angle which is equal to its supplement.
Answer
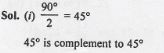

Question 6
Two complementary angles are (x + 4)° and (2x – 7)°, find the value of x.
Answer
(x + 4)° and (2x – 7)° are complementary angles
x + 4 + 2x – 7 = 90°
⇒ 3x – 3 = 90°
⇒ 3x = 90° + 3 = 93°
x = 31°
Question-7
Two supplementary angles are in the ratio of 2 : 7, find the angles.
Solution:
Two supplementary angles in the ratio 2 : 7 and sum is 180°
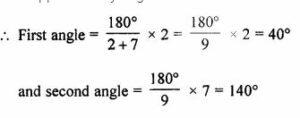
Question 8
Among two supplementary angles, the measure of the longer angle is 44° more than the measure of the smaller angle. Find their measures.
Answer
Sum of two supplementary angles = 180°
Let smaller angle = x Then second angle = x + 44°
x + x + 44° = 18°
⇒ 2x = 180° – 44° = 136°
⇒ 2x = 136°
⇒ x = 68°
One angle = 68°
and second angle = 68° + 44° = 112°
Question 9
If an angle is half of its complement, find the measure of angles.
Answer
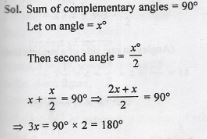
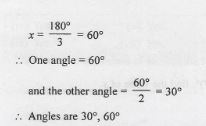
Question 10
Two adjacent angles are in the ratio 5 : 3 and they together form an angle of 128°, find these angles.
Answer
Sum of two adjacent angles = 128°
and ratio between them = 5 : 3
Let first angle = 5x
Then second angle = 3x
5x + 3x = 128°
⇒ 8x = 128°
⇒ x = 16°
First angle = 5x = 5 × 16° = 80°
and second angle = 3x = 3 × 16 = 48°
Answer

Question 11
Find the value of x in each of the following diagrams:
………
Answer
In the given figure,
(i) 105° + 41° + x° + 130° = 360°
(Angles at a point)
⇒ 276° + x = 360°
⇒ x = 360° – 276° = 84°
⇒ x = 84°
(ii) In the given figure,
3x + x + 40° = 180°
(Angles on one side of a straight line)
⇒ 4x = 180° – 40° = 140°
⇒ x = 35°
(iii) In the given figure,
2x+ 10 + 3x – 10 + 40 = 180°
(Angles on one side of a straight line)
⇒ 5x + 40° = 180°
⇒ 5x = 180° – 40° = 140°
x = 28°
Question 12
Find the values of x, y and z in each of the following diagrams
……………
Answer
(i) In the given figure,
Given ∠ = 135°
y = 135° (Vertically opposite angles)
But x + y = 180° (Linear pair)
⇒ x + 135° = 180°
⇒ x = 180° – 135° = 45°
But z = x (Vertically opposite angles)
z = 45°
Hence, x = 45°, y = 135°, z = 45°
(ii) In the given figure,
Given ∠ = 31°
x = 31° (Vertically opposite angles)
But 31° + y + 90° = 180°
(Angles on one side of a straight line)
⇒ y + 121° = 180°
⇒ y = 180° – 121° = 59°
But z = y (Vertically opposite angles)
z = 59°
Hence, x = 31°, y = 59°, z = 59°
(iii) In the given figure,
Given ∠s are 51° and 44°
Let ∠1 = 44° and ∠2 = 51°
x = 44° (Vertically opposite angles)
and ∠2 = ∠z, z = 51° (Vertically opposite angles)
∠1 = ∠x
But x + y + z = 180° (Angles on one side of a line)
⇒ 44° + 51° + y= 180°
⇒ 95° + y = 180°
⇒ y = 180° – 95° = 85°
y = 85°, z = 51°
Hence, x = 44°, y = 85°, z = 51°
Question 13
In the given figure, lines AB and CD intersect at F. If ∠EFA = ∠AFD and ∠CFB = 50°, find ∠EFC
Answer
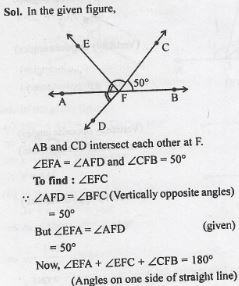
⇒ 50° + ∠EFC + 50° = 180°
⇒ ∠EFC + 100° = 180°
⇒ ∠EFC =180° – 100° = 80°
⇒ ∠EFC = 80°
Lines and Angles Class-7 ML Aggarwal ICSE Mathematics Solutions Exercise- 10.2
Question 1
Identity each of the given pair of angles as alternate interior angles, co-interior angles or corresponding angles or none of these in the given figure:

(i) ∠2, ∠6
(ii) ∠1, ∠6
(iii) ∠3, ∠5
(iv) ∠2, ∠7
(v) ∠3, ∠6
(vi) ∠4, ∠8
Answer
(i) ∠2 and ∠6 – are corresponding angles.
(ii) ∠1 and ∠6 – none
(iii) ∠3 and ∠5 – alternate interior angles
(iv) ∠2 and ∠7 – none
(v) ∠3 and ∠6 – co-interior angles
(vi) ∠4 and ∠8 – corresponding angles
Question 2
State the property that is used in each of the following statements:
(i) If a || b, then ∠1 = ∠5.
(ii) If ∠4 = ∠6, then a || b.
(iii) If ∠4 + ∠5 = 180°, then a || b.

Answer
In the given figure,
(i) If a || b, then
∠1 = ∠5 (Property of the corresponding pair of angles)
(ii) If ∠4 = ∠6
Property of interior alternate angles are equal
a || b
(iii) If ∠4 + ∠5 = 180°
Property of co-interior angles are supplementary, then a || b.
Question 3
In each of the following figures, a pair of parallel lines is cut by a transversal. Find the value of x
Answer
(i) In the given figure,
x = 100 (Corresponding angles)
(ii) x + 110° = 180°
(Cointerior Angles are Supplementary)
x = 180° – 110° = 70°
(iii) Let ∠1 opposite to ∠110°
∠1 = 110° (Vertically opposite angles)
and ∠1 + x = 180°
(Cointerior Angles are Supplementary)

⇒ 110° + x = 180°
⇒ x = 180° – 110°
⇒ x = 70°
Question 4
In the following figures, a pair of parallel lines are cut by a transversal. Find the value of x in each figure.
Answer
(i) AB || CD and EF its transversal
⇒ ∠AGH + ∠GHC = 180°
⇒ 2x + 60 + 3x + 54° = 180°
(Sum of co-interior angles)
⇒ 5x + 60° = 180°
⇒ 5x = 180° – 60° = 120°
⇒ x = 24°
x = 24°

(ii) AB || CD and EF is its transversal
Which intersects them at G and H.
∠HGB = ∠FHD (Corresponding angles)
∠HGB = 3x + 30°
But ∠AGH + ∠HGB = 180° (Linear pair)
2x+ 15° + 3x + 30° = 180°
⇒ 5x + 45° = 180°
⇒ 5x = 180° – 45° = 135°
⇒ 5x = 135°
⇒ x = 27°
x = 27°
Question 5
In the following figures (i) to (vi), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle.
Answer
In the given figure,
(i) Given angle is 60°
x = 60° (Vertically opposite angles)
But ∠y = ∠x (corresponding angles)
∠y = 60°
Hence, ∠x = 60°, ∠y = 60°
(ii) In the given figure,
Given angle is 135°
∠q = 135° (Vertically opposite angles)
But ∠p + ∠q = 180° (Sum of cointerior angles)
135° + ∠q = 180°
∠q = 180° – 135° = 45°
∠p = 45,°, ∠q = 135°
(iii) In the given figure,
Given angle is 70°
a = 70° (Alternate angles)
But ∠a + ∠b = 180° (Linear pair)
70° + ∠b = 180°
∠b = 180° – 70° = 110°
∠a = 70°, ∠b = 110°
(iv) In the given figure,
Given angle is 128°
∠x + 128° = 180° (Linear pair)
∠x = 180° – 128° = 52°
But ∠x = ∠y (Corresponding angles)
∠y = 52°
Also, y + z = 180° (Linear pair)
52° + ∠z = 180°
∠z = 180° – 52°
∠z = 128°
Hence, x = 52°, y = 52°, z = 128°
(v) In the given figure,
Given angle is 75°
∠a + 75° = 180° (Linear pair)
∠a = 180° – 75° = 105°
∠b = 75° (Vertically opposite angles)
∠c = 75° (Corresponding angles)
But ∠c + ∠d = 180° (Linear pair)
75° + ∠d = 180°
∠d = 180° – 75° = 105°
∠a = 105°, ∠b = 75°, ∠c = 75°, ∠d = 105°
(vi) Given angle = 62°
62 ° + ∠q = 180° (Linear pair ∠s)
∠q = 180° – 62° = 118°
∠p = 62° (Vertically opposite ∠s)
∠s = p (Corresponding ∠s)
∠s = 62°
∠s + ∠r = 180° (Linear pair ∠s)
62° + ∠r = 180°
∠r = 180° – 62° = 118°
Question 6
In the given diagram, lines AB, CD and EF are parallel. Calculate the values of x and y. Hence, find the reflex angle ECA
Answer
In the given figure,
AB || CD || EF
∠E = 120°, ∠A = 140°
y + 140° = 180° (Sum of co-interior angles)
y = 180° – 140° = 40°
Similarly, x + 120° = 180°
x = 180° – 120° = 60°
x = 60°, y = 40°
Now, ∠ECA = x + y = 60° + 40° = 100°
and reflex ∠ECA = 360° – 100° = 260°
Question 7
In the given figure, l || m. Find the values of x, y and z.
Answer
In the given figure, x = 45° (Alternate angles)
Similarly, z = 55° (Alternate angles)
But x + y + z = 180°
(Angles on the one side of a straight line)
⇒ 45° + y + 55° = 180°
⇒ y + 100° = 180°
⇒ y = 180° – 100° = 80°
x = 45°, y = 80°, z = 55°
Question 8
Calculate the measure of each lettered angle in the following figure (parallel lines, segment or rays are denoted by thick matching arrows):
Answer
(i) In the given figure,
∠x + 143° = 180°
(Sum of co-interior angles)
∠x = 180° – 143° = 37°
Similarly, ∠z + 60° = 180°
∠y = 180° – 60° = 120°
But ∠x + ∠y + ∠z = 180°
(Angles on one side of a straight line)
37° + 120° + ∠y = 180°
157° + ∠y = 180°
∠y = 180° – 157° = 23°
∠x = 37°, ∠y = 23°, ∠z = 120°
(ii) In the given figure,
∠c = 72° (Alternate angles)
∠a = 55° (Corresponding angles)
But ∠b + ∠c + 55° = 180°
(Angles on one side of a straight line)
∠b + 72° + 55° = 180°
∠b + 127° = 180°
∠b = 180° – 127° = 53°
Here, ∠a = 55°, ∠b = 53°, ∠c = 72°
(iii) In the given figure,
∠a + 75° = 180° (Linear pair)
∠a = 180° – 75° = 105°
∠b = 75° (Alternate angles)
∠d = b (Corresponding angles)
∠d = 75°
75° = ∠c (Corresponding angles)
∠c = 75°
∠a = 105°, ∠b = 15°, ∠c = 75°, ∠d = 75°
Question 9
In the figure given below, state whether the lines l and m are parallel or not.

Answer
i) In the given figure,

∠106° and ∠64° are co-interior angles
106° + 64° = 170°
Sum of co-interior angles is not equal to 180°
l and m are not parallel
(ii) ∠1 = 75° (Vertically opposite angles)
But ∠1 and 75° are co-interior angles
and ∠1 + 75° = 75° + 75° = 150°

It the sum is not equal to 180°
l and m are not parallel
(ii) ∠1 = 57° (Vertically opposite angles)

∠1 + 123° = 57° + 123° = 180° (Sum of co-interior)
∠1 + 123° = 180°
l || m
ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 10 Lines and Angles Objective Type Questions
Mental Maths
Question 1
Fill in the blanks:
(i) If two angles are complementary, then the sum of their measures is ………..
(ii) If two angles are supplementary, then the sum of their measures is …………
(iii) Supplement of an obtuse angle is ……….
(iv) Two angles forming a linear pair are ……….
(v) If two adjacent angles are supplementary, then they form a ………..
(vi) Angles of a linear pair are as well as ………..
(vii) Adjacent angles have a common vertex, a common ……….. and no common ………
(viii)Angles formed by two intersecting lines having no common arms are called ………..
(ix) If two lines intersect and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are ……..
(x) Two lines in a plane which never meet are called ……….
(xi) Alternate interior angles have one common …………
(xii) Corresponding angles are on the ……….. side of the transversal.
(xiii) Alternate interior angles are on the ………… side of the transversal.
(xiv) If two lines are cut by a transversal such that a pair of corresponding angles are not equal, then the lines are ………..
Answer
(i) If two angles are complementary,
then the sum of their measures is 90°.
(ii) If two angles are supplementary,
then the sum of their measures is 180°.
(iii) Supplement of an obtuse angle is an acute angle.
(iv) Two angles forming a linear pair are supplementary.
(v) If two adjacent angles are supplementary,
then they form a linear pair.
(vi) Angles of a linear pair are adjacent as well as supplementary.
(vii) Adjacent angles have a common vertex,
a common arm, and no common interior points.
(viii) Angles formed by two intersecting lines having
no common arms are called vertically opposite angles.
(ix) If two lines intersect and if one pair of vertically opposite angles
are acute angles, then the other pair of vertically opposite angles are obtuse angles.
(x) Two lines in a plane which never meet are called parallel lines.
(xi) Alternate interior angles have one common arm.
(xii) Corresponding angles are the same side of the transversal.
(xiii) Alternate interior angles are on the opposite side of the transversal.
(xiv) If two lines are cut by a transversal such that a pair of
corresponding angles are not equal, then the lines are not parallel.
Question 2
In the given figure, AB is a straight line and OD ⊥ AB. Observe the figure and fill in the following blanks:

(i) ∠AOC and ∠COE form a pair of ……….. angles.
(ii) ∠AOC and ∠COB are ……….. angles.
(iii) ∠AOC is ………… of ∠COD.
(iv) ∠BOE is …………. of ∠EOA.
Answer
In the given figure,
AB is a straight line and OD ⊥ AB
(i) ∠AOC and ∠COE form a pair of adjacent angles.
(ii) ∠AOC and ∠COB are supplementary angles.
(iii) ∠AOC is the complement of ∠COD.
(iv) ∠BOE is a supplement of ∠EOA.
Question 3
State whether the following statements are true (T) or false (F):
(i) Two obtuse angles can be supplementary.
(ii) Two acute angles can form a linear pair.
(iii) Two obtuse angles can form a linear pair.
(iv) Two adjacent angles always form a linear pair.
(v) Pair of vertically opposite angles are always supplementary.
(vi) 30° is one-half of its complement.
(vii) If two lines are cut by a transversal,
then each pair of corresponding angles are equal.
(viii) If two lines are cut by a transversal,
then each pair of alternate interior angles are equal.
Answer
(i) Two obtuse angles can be supplementary. (False)
Correct:
As the sum of two obtuse angles is greater than 180°.
(ii) Two acute angles can form a linear pair. (False)
Correct:
As the sum of two acute angles is less than 180°.
(iii) Two obtuse angles can form a linear pair. (False)
Correct :
As the sum of two obtuse angles is greater than 180°.
(iv) Two adjacent angles always form a linear pair. (False)
Correct:
As the sum of two adjacent angles can be less than 180° or more than 180°.
(v) Pair of vertically opposite angles are always supplementary. (False)
(vi) 30° is one-half of its complement. (True)
(30° and 60° are complement and 30° = × 60°)
(vii) If two lines are cut by a transversal,
then each pair of corresponding angles are equal. (False)
Correct:
It may or may not be equal.
If lines are parallel than the corresponding angle are the same
and if lines are not parallel than angles are different.
(viii) If two lines are cut by a transversal,
then each pair of alternate interior angles are equal. (False)
Correct :
If the two lines are parallel, then it is possible.
Otherwise, these angles are different.
Multiple Choice Question (MCQ)
Question 4
A pair of complementary angles is
(a) 130°, 50°
(b) 35°, 55°
(c) 25°, 75°
(d) 27°, 53°
Answer
A pair of complementary angles is 35°, 55°.
As the sum of complementary angles is 90°. (b)
Question 5.
A pair of supplementary angles is
(a) 55°, 115°
(b) 65°, 125°
(b) 47°, 133°
(d) 40°, 50°
Answer
A pair of supplementary angles is 47°, 133°.
As the sum of supplementary angles is 180°. (c)
Question 6
If an angle is one-third of its supplement, then the measure of the angle is
(a) 45°
(b) 30°
(c) 135°
(d) 150°
Answer
If one angle is one-third of its supplement,
then the measure of an angle is 45°. (a)
Let first angle = x°

x = = 135°
Question 7
If an angle measures 10° more than its complement, then the measure of the angle is
(a) 40°
(b) 55°
(c) 35°
(d) 50°
Answer
If one angle measures 10° more than its complement,
then measure of the angle = 50°.
(∵ 50° + 40° = 90°)
Question 8.
If one angle of a linear pair is acute, then the other angle is
(a) acute
(b) obtuse
(c) right
(d) straight
Answer
If one angle of a linear pair is acute,
then the other angle will be obtuse.
(∵ Linear pair = 180°) (b)
Question 9.
In the given figure, the value of x that will make AOB a straight line is
(a) x = 40
(b) x = 35
(c) x = 30
(d) x = 25

Answer
AOB will be a straight line if
3x + 15 + 2x – 10° = 180°
⇒ 5x + 5 = 180°
⇒ 5x = 180° – 5 = 175°
⇒ x = 35° (b)
Question 10.
If two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of transversal is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
Two lines are intersected by a transversal then a number of
pairs of interior angles on the same side of the transversal is two. (b)
Question 11.
In the given figure, if l || m then the value of x is
(a) x = 50
(b) x = 60
(c) x = 70
(d) x = 45

Answer
In the given figure, l || m
110° = 3x – 40°
⇒ 3x = 110° + 40° = 150°
x = 50° (a)
Question 12.
In the gitsen figure, if l || m then the value of x is
(a) x = 75°
(b) x = 95°
(c) x = 105°
(d) x = 115°

Answer
In the given figure, l || m
∠1 = 75° (Vertically opposite angles)
and ∠1 + x = 180° (Co-interior angles)
x + 75° = 180°
x = 180° – 75° = 105° (c)

Question 13.
In the given figure, AB || CD. If ∠APQ = 50° and ∠PRD = 130°, then ∠QPR is
(a) 30°
(b) 50°
(c) 80°
(d) 130°

Answer
In the given figure,
AB || CD, ∠APQ = 50°
∠PRD = 130°, ∠QPR = ?
AB || CD
∠APQ = ∠PQR (Alternate angles)
∠PQR = 50°
∠PRD + ∠PRQ = 180° (Linear pair)
130° + ∠PRQ = 180°
∠PRQ = 180° – 130° = 50°
Now in ∆PQR
∠PQR + ∠PRQ + ∠QPR = 180° (Angles of a triangle)
50° + 50° + ∠QPR = 180°
∠QPR = 180° – 50° – 50° = 80° (c)
Question 14.
In the given figure, PA || BC || DQ and AB || DC. Then the values of x and y are respectively:
(a) 50°, 120°
(b) 50°, 130°
(c) 60°, 120°
(d) 60°, 130°

Answer
In the given figure,
PA || BC || DQ
AB || DC
x = 50° (Alternate angles)
∠BCD + ∠ABC = 180° (Sum of co-interior angles)
⇒ ∠DCB + 50° = 180°
⇒ ∠DCB = 180° – 50° = 130°
BC || DQ
∠DCB = ∠CDQ (Alternate angles)
y = 130°
x = 50°, y = 130° (b)
Higher Order Thinking Skills ( HOTS )
Question
Calculate the measure of each lettered angle in the following figures (parallel line segments / rays are denoted by thick matching arrows):

Answer
(i) In the given figure,
Given ∠s are 72° and 55°
a = 55° (Corresponding angles)
c = 72° (Alternate angles)
But b + c + 55° = 180°
(Angles on the one side of a straight line)
⇒ b + 72° + 55° = 180°
⇒ b + 127° = 180°
⇒ b = 180° – 127° = 53°
a = 55, b = 53°, c = 72°
(ii) In the given figure,

Give ∠s are 135° and 110°
p = 135° (Alternate angles)
p + r + 110° = 360° (Angles at a point)
⇒ 135° + 110° + r = 360°
⇒ 245° + r = 360°
⇒ r = 360° – 245° = 115°
But r + q = 180° (Co-interior angles)
⇒ 115° + q = 180°
⇒ q = 180° – 115° = 65°
p = 135°, q = 65°, r = 115°
(iii) In the given figure,
Given angle is 110°
p = ∠1 (Vertically opposite angles)
But ∠1 + 110° = 180° (Co-interior angles)
⇒ ∠1 = 180° – 110° = 70°
⇒ p = ∠1 = 70°
s = 110° (Alternate angles with 110°)
p = q (Corresponding angles)
q = 70°
r = q (Alternate angles)
r = 70°
Now, p = 70°, q = 70°, r = 70°, s = 110°
Check Your Progress
Question 1.
Find the supplementary angle of each of the following angles:
(i) of 90°
(ii) of 280°
Answer
(i) of 90° = 45°
Supplementary angle of 45° = 180° – 45° = 135°
Hence, supplementary angle of of 95° is 135°.
(ii) of 280° = 120°
Supplementary of 120° is 180° – 120° = 60°
Question 2.
How many degrees are there in an angle which is one-fifth of its complement?
Answer
Let one angle = x
But it is th of its complementary angle
Complementary angle = 5x
x + 5x = 90°
⇒ 6x = 90°
⇒ x = 15°
Required angle = 15°
Question 3
If two angles are supplementary and one angle is 5° more than four-times the other, find the angles.
Answer
Let one angle of supplementary angles = x
The second = 4x + 5°
x + 4x + 5° = 180°
⇒ 5x = 180° – 5 = 175°
⇒ x = 35°
One angle = 35°
and other angle = 180° – 35° = 145°
Question 4
The given diagram shows two intersecting straight lines. Find the values of x, y and z.

Answer
In the given figure,
2x + 15 = 3x – 10° (Vertically opposite angles)
⇒ 3x – 2x = 15° + 10°
⇒ x = 25°
Now, y + 2x + 15° = 180° (Linear pair)
y + 2 × 25° + 15° = 180°
⇒ y + 50° + 15° = 180°
⇒ y + 65° = 180°
⇒ y = 180° – 65° = 115°
and z = y = 115° (Vertically opposite angles)
x = 25°, y = 115°, z = 115°
Question 5
In the given diagram, lines AB and CD intersect at O. If ∠1 + ∠3 = 78°, find the size of ∠2.

Answer
In the given figure,
AB and CD intersect each other at O
∠1 + ∠3 = 78°
But ∠1 = ∠3 (Vertically opposite angles)
∠1 = ∠3 = = 39°
But ∠1 + ∠2 = 180° (Linear pair)
39° + ∠2 = 180°
∠2 = 180° – 39° = 141°
∠2 = 141°
Question 6
(a) In the figure (i) given below, l || m. If ∠5 = 65°, find all other angles.
(b) In the figure (ii) given below, l || m. Find the values of x, y and z.
(c) In the figure (iii) given below, l || m and p || q. Find the values of x, y and z.

Answer
In the given figure, l || m
∠5 = 65°
∠5 = ∠3 (Alternate angle)
∠3 = 65°
∠5 = ∠1
∠1 = 65°
∠4 + ∠5 = 180° (Sum of co-interior angle)
∠4 + 65° = 180°
∠4 = 180° – 65° = 115°
∠2 = ∠4 = 115° (Vertically opposite angles)
∠6 = ∠4 = 115° (Alternate angles)
∠6 = ∠8 = 115° (Vertically opposite angles)
∠7 = ∠5 = 65° (Vertically opposite angles)
∠1 = 65°, ∠2 = 115°, ∠3 = 65°, ∠4 = 115° ∠6 = 115°,
∠7 = 65°, ∠8 = 115°
(ii) In the given figure, l || m
Given ∠s are 40° and 105°
x = 40° (Alternate angles)
z + 105° = 180° (Sum of co-interior angles)
⇒ z = 180°- 105° = 75°
Now, 40° + y + z = 180°
(Angles on one side of a straight line)
⇒ 40° + y + 75° = 180°
⇒ y + 115° = 180°
⇒ y – 180° – 115° = 65°
x = 40°, y = 65°, z = 75°
(iii) In the given figure,
Given angle is 105°
x + 105° = 180°
x = 180° – 105° = 75°
But x + y = 180° (Sum of co-interior anlges)
⇒ 75° + y = 180° (Sum of co-interior anlges)
⇒ y = 180° – 75° = 105°
Similarly, y + z = 180° (Sum of co-interior anlges)
⇒ 105° + z = 180°
⇒ z = 180° – 105° = 75°
Hence, x = 75°, y = 105°, z = 75°
— End of Lines and Angles Class-7 ML Aggarwal Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -7
Thanks


