Maths Specimen Paper Sec-B 2023 Solved for ICSE Class-10

Maths Specimen Paper Sec-B 2023 Solved for ICSE Class-10.  Step by step solutions as council prescribe guideline of model sample question paper.  During solutions of Maths specimen paper we explain with figure , graph, table whenever necessary so that student can achieve their goal in next upcoming exam of council. Visit official website CISCE for detail information about ICSE Board Class-10.

ICSE Class-10 Maths Specimen Paper 2023 Solved sec-B

Board	ICSE
Class	10th (x)
Subject	Maths (Section-B)
Topic	ICSE Specimen Paper Solved
Syllabus	on bifurcated syllabus (after reduction)
session	2022-23
Question Type	Descriptive Type (as prescribe by council)
Total question	10 with all parts (Sec-A&B)
Max mark	80

ICSE Maths Specimen Paper 2023 Solved Class-10

Warning :- before viewing solution view Question Paper

---

ICSE SPECIMEN QUESTION PAPER 2023

MATHEMATICS

Maximum Marks: 80

• Time allowed: Two and half hours Answers to this Paper must be written on the paper provided separately.
• You will not be allowed to write during first 15 minutes.
• This time is to be spent in reading the question paper.
• The time given at the head of this Paper is the time allowed for writing the answers.

---

Attempt all questions from Section A and any four questions from Section B.

• All working, including rough work, must be clearly shown, and must be done on the same sheet as the rest of the answer.
• Omission of essential working will result in loss of marks. The intended marks for questions or parts of questions are given in brackets [ ]
• Mathematical tables are provided.

---

SECTION B Maths ICSE Specimen Paper Solved 2023 Class-10

(Attempt any four questions from this Section.)

Question 4:
(i) The following bill shows the GST rates and the marked price of articles:

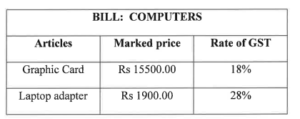
Find the total amount to be paid for the above bill.

(ii) Solve the following quadratic equation,

7x² +2x-2=0

Give your answer correct to two places of decimal

(iii) Use graph sheet for this question. Draw a histogram for the daily earnings of 54 medical stores in the following table and hence estimate the mode for the following distribution. Take 2 cm = Rs. 500 units along the x-axis and 2 cm = 5 stores along the y-axis.

Question 5:

(i)

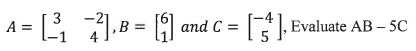
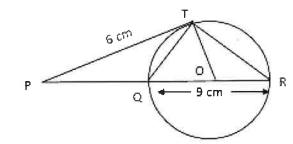
(ii) In the given figure, O is the centre of circle. The tangent PT meets the diameter RQ [3]
produced at P.

(a) Prove Triangle PQT ~ Triangle PTR

(b) If PT =6cm,QR =9cm. Find the length of PQ

(iii) Factorise the given polynomial completely, using Remainder Theorem:

6x³ + 25x² + 31x + 10

Question 6:

(i) ABCD is a square where B (1, 3), D (3, 2) are the end points of the diagonal BD.

Find:

(a) the coordinates of point of intersection of the diagonals AC and BD
(b) the equation of the diagonal AC

(ii) Prove that : 

(iii) The first, the last term and the common difference of an Arithmetic Progression are 98, 1001 and 7 respectively. Find the following for the given Arithmetic Progression:

(a) number of terms ‘n’.
(b) Sum of the ‘n’ terms.

Question 7:

(i) A box contains some green, yellow and white tennis balls. The probability of selecting a green ball is 1/4 and yellow ball is 1/3 If the box contains 10 white balls, then find:

(a) total number of balls in the box.
(b) probability of selecting a white ball.

(ii) A cone and a sphere having the same radius are melted and recast into a cylinder. The radius and height of the cone are 3 cm and 12 cm respectively. If the radius of the cylinder so formed is 2 cm, find the height of the cylinder.

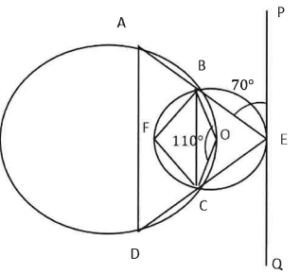
(iii) In the given diagram, ABCD is a cyclic quadrilateral and PQ is a tangent to the smaller circle at E. Given angle AEP = 70°, angle BOC = 110°. Find:

(a) angle ECB,
(b) angle BEC,
(c) angle BFC,
(d) angle DAB,

Question 8:

(i) Solve the following inequation:

Represent the solution set on a number line.

(ii) The following table gives the petrol prices per litre for a period of 50 days.

Find the mean price of petrol per litre to the nearest rupee using step — deviation method.

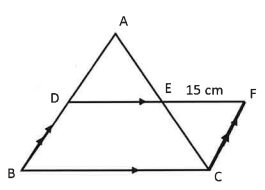
(iii) In the given diagram, ABC is a triangle and BCFD is a parallelogram.

AD: DB = 4:5 and EF = 15 cm.

Find:

(a) AE:EC

(b) DE

(c) BC

Question 9:

(i) Amit takes 12 days less than the days taken by Bijoy to complete a certain work. If both, working together, takes 8 days to complete the work, find the number of days taken by Bijoy to complete the work, working alone.

(ii) Use a graph sheet for this question. The daily wages of 120 workers working at a site are given below:

Use 2cm = % 50 and 2 cm = 20 workers along x — axis and y — axis respectively to

draw an ogive and hence estimate:
(a) the median wages
(b) the inter — quartile range of wages

(c) percentage of workers whose daily wage is above rs. 475.

Question 10:

(i) Solve for x, using the properties of proportion.

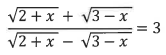
(ii) Using ruler and compasses, construct a regular hexagon of side 4.5 cm. Hence construct a circle circumscribing the hexagon. Measure and write down the length of the circum-radius.

(iii) An observer standing on the top of a lighthouse 150 m above the sea level watches a ship sailing away. As he observes, the angle of depression of the ship changes from 50° to 30°. Determine the distance travelled by the ship during the period of observation. Give your answer correct to the nearest meter. (Use Mathematical Table for this question.

PDF Solution of Sec-B ICSE Maths Specimen Paper 2023

–: Visit also :–

Return to : ICSE Specimen Paper 2023 Solved

Thanks