Matrices Selina Concise Solutions Chapter 9 for ICSE Class 10. Solutions of Exercise – 9 (A), Exercise – 9 (B), Exercise – 9 (C), Exercise – 9 (D), for Concise Selina Maths for ICSE Board Class 10th. Concise Solutions Matrices Chapter – 9 for ICSE Maths Class 10 is available here. All Solutions of Concise Selina of Chapter 9 Matrices has been solved according instruction given by council. This is the Solutions of Chapter-9 Matrices for ICSE Class 10th. ICSE Maths text book of Concise is In series of famous ICSE writer in maths. Concise is most famous among students.
Matrices Selina Concise Solutions Chapter 9 for ICSE Class 10
The Solutions of Concise Mathematics Chapter 9 Matrices for ICSE Class 10 have been solved. Experience teachers Solved Chapter-9 Matrices to help students of class 10th ICSE board. Therefore the ICSE Class 10th Maths Solutions of Concise Selina Publishers helpful on various topics which are prescribed in most ICSE Maths textbooks
Select Topics of Chapter- 9 Matrices Selina Concise Solutions
How to Solve Concise Maths Selina Publications Chapter-9 Matrices
Note:- Before viewing Solutions of Chapter -9 Matrices of Concise Selina Maths read the Chapter Carefully then solve all example of your text book. The Chapter- 9 Matrices is main Chapter in ICSE board .
Exercise – 9 (A) , of Chapter-9 Matrices for Concise Solutions for ICSE Class 10th Mathematics ( Selina Publishers)
Question 1
State, whether the following statements are true or false. If false, give a reason.
(i) If A and B are two matrices of orders 3 2 and 2 3 respectively; then their sum A + B is possible.
(ii) The matrices and are conformable for subtraction.
(iii) Transpose of a 2 1 matrix is a 2 1 matrix.
(iv) Transpose of a square matrix is a square matrix.
(v) A column matrix has many columns and one row.
Answer 1
(i) False
The sum A + B is possible when the order of both the matrices A and B are same.
(ii) True
(iii) False
Transpose of a 2 1 matrix is a 1 2 matrix.
(iv) True
(v) False
A column matrix has only one column and many rows.
Question 2
Given: ,………… find x, y and z.
Answer 2
If two matrices are equal, then their corresponding elements are also equal. Therefore, we have:
x = 3,
y + 2 = 1 y = -1
z – 1 = 2 z = 3
Question 3
Solve for a, b and c if………….
Answer 3
If two matrices are equal, then their corresponding elements are also equal.
(i)
a + 5 = 2 a = -3
-4 = b + 4 b = -8
2 = c – 1 c = 3
(ii) a= 3
a – b = -1
b = a + 1 = 4
b + c = 2
c = 2 – b = 2 – 4 = -2
Question 4
If A = and B = ; find: (i) A + B (ii) B – A
Answer 4
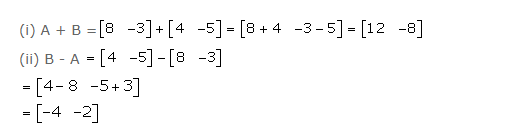
Question 5
If A=…….., B = ………and C =…….; find:
(i) B + C (ii) A – C
(iii) A + B – C (iv) A – B +C
Answer 5
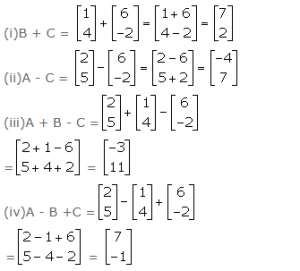
Question 6
Wherever possible, write each of the following as a single matrix………………
Answer 6
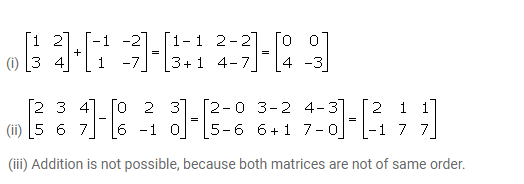
Question 7
Find, x and y from the following equations :……………..
Answer 7
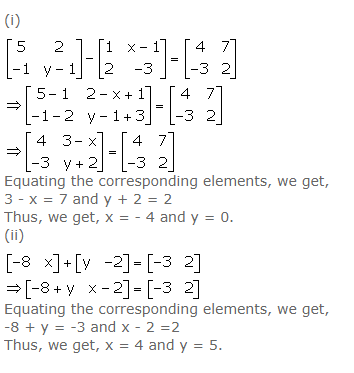
Question 8
Given: M =…………. , find its transpose matrix Mt. If possible, find:
(i) M + Mt (ii) Mt – M
Answer 8
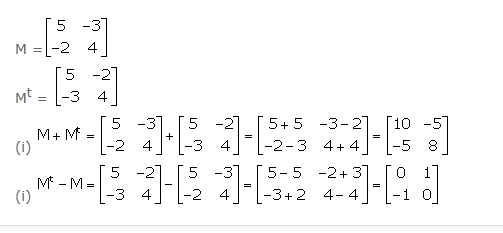
Question 9
Write the additive inverse of matrices A, B and C:
Where ……………..
Answer 9

Question 10
Given ……………………; find the matrix X in each of the following:
(i) X + B = C – A
(ii) A – X = B + C
Answer 10
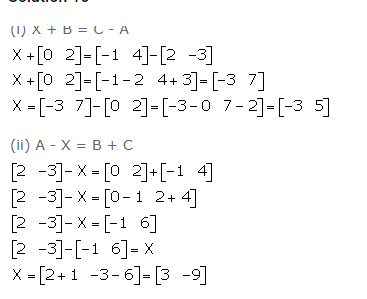
Question 11
Given ………………; find the matrix X in each of the following:
(i) A + X = B
(ii) A – X = B
(iii) X – B = A
Answer 11
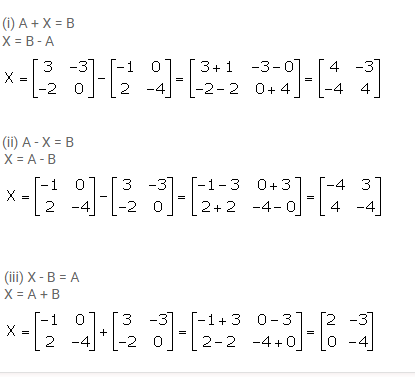
Chapter-9 Matrices Exercise -9 (B) for Selina Concise Solutions for ICSE Class 10th Mathematics ( Selina Publishers)
Question 1
Evaluate:…………….
Answer 1
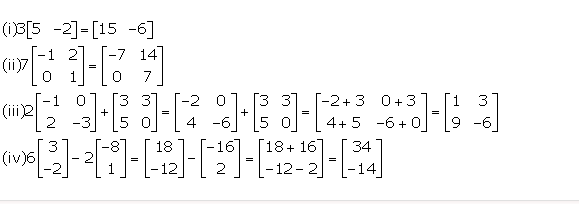
Question 2
Find x and y if:………………
Answer 2

Question 3
Given ; find:………………….
(i) 2A – 3B + C
(ii) A + 2C – B
Answer 3

Question 4
If……………..
Answer 4
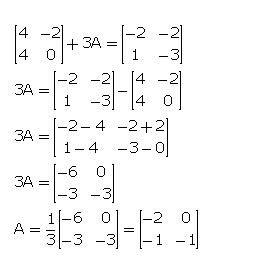
Question 5
Given ……………..
(i) find the matrix 2A + B
(ii) find the matrix C such that:
C + B = …………..
Answer 5

Question 6
If…………… ; find the values of x, y and z.
Answer 6

Question 7
Given A = ………………and At is its transpose matrix. Find:
(i) 2A + 3At (ii) 2At – 3A
(iii) ………….(iv) …………….
Answer 7
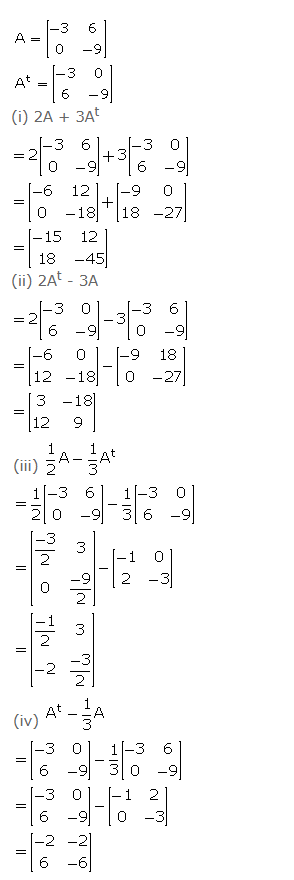
Question 8
Given ………………..
Solve for matrix X:
(i) X + 2A = B
(ii) 3X + B + 2A = O
(iii) 3A – 2X = X – 2B.
Answer 8
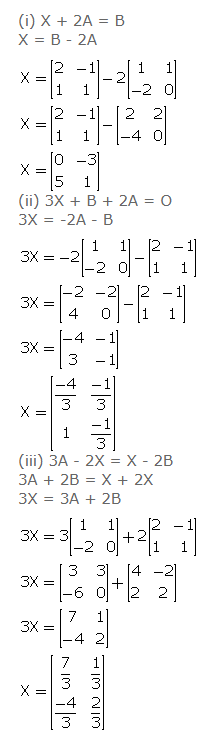
Question 9
If ………….., show that
3M + 5N = …………..
Answer 9

Question 10
If I is the unit matrix of order 2 x 2; find the matrix M, such that:
(i) M – 2I = …………
(ii) 5M + 3I =………….
Answer 10
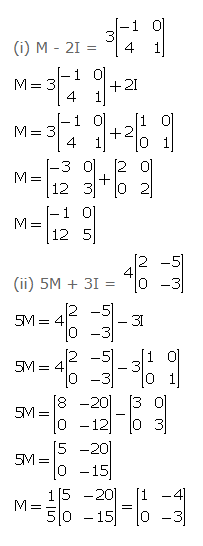
Question 11
If ………………find matrix M
Answer 11

Chapter 9 – Matrices, Exercise. 9 (C) Concise Solutions (Selina Publishers)
Question 1
Evaluate: if possible:………….
Answer 1

Question 2
If ………………and I is a unit matrix of order 2 2, find:
(i) AB (ii) BA (iii) AI
(iv) IB (v) A2 (vi) B2A
Answer 2
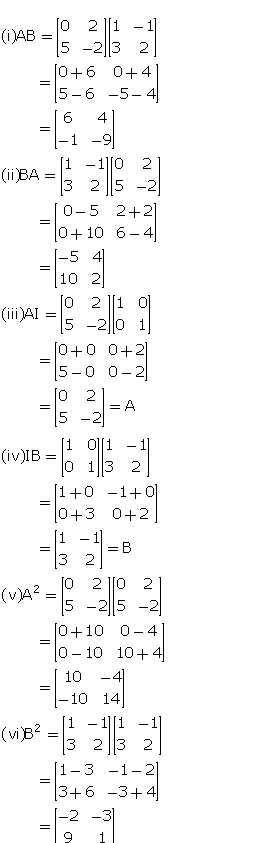

Question 3
If…………………………………
Answer 3
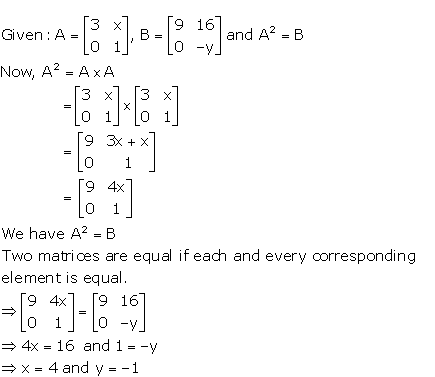
Question 4
Find x and y, if:…………………..
Answer 4

Question 5
If …………., find:
(i) (AB)C (ii) A(BC)
Is A(BC) = (AB)C?
Answer 5

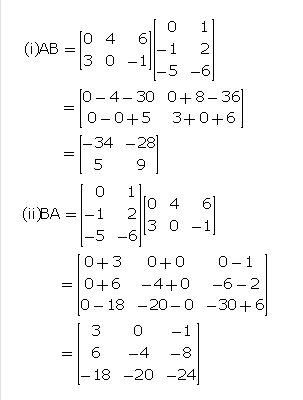
Question 6
Given ,…………. find; if possible:
(i) AB (ii) BA (iii)A2
Answer 6
Question 7
If………..find …..
Answer 7
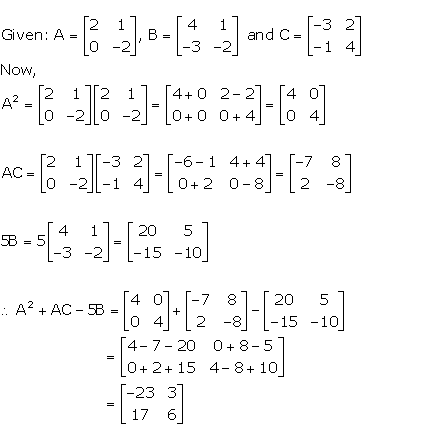
Question 8
If M = ………….. and I is a unit matrix of the same order as that of M; show that:
M2 = 2M + 3I
Answer 8
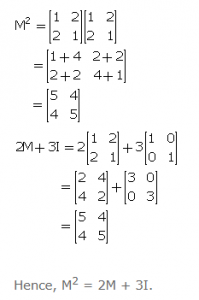
Question 9
If …………………. and BA= M2, find the values of a and b.
Answer 9

Question 10
Given ………………., find:
(i) A – B (ii) A2
(iii) AB (iv) A2 – AB + 2B
Answer 10

Question 11
If ……………….; find:
(i) (A + B)2 (ii) A2 + B2
(iii) Is (A + B)2 = A2 + B2?
Answer 11

Question 12
Find the matrix A…………, if B = and B2 = B + ………A.
Answer 12
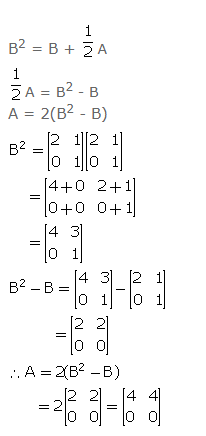
Question 13
If A = ………….and A2 = I; find a and b.
Answer 13

Question 14
If ………….; then show that:
(i) A (B + C) = AB + AC
(ii) (B – A)C = BC – AC.
Answer 14

Question 15
If…………… , simplify:
A2 + BC.
Answer 15
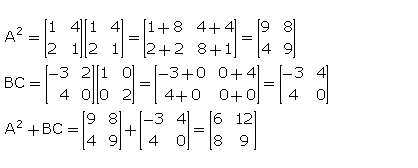
Question 16
Solve for x and y:…………
Answer 16
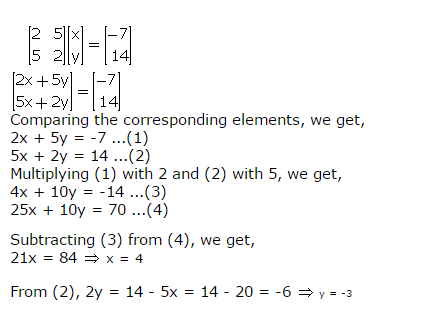
Question 17
In each case given below, find :
(a) the order of matrix M.
(b) the matrix M.
(i)………..
(ii)………..
Answer 17
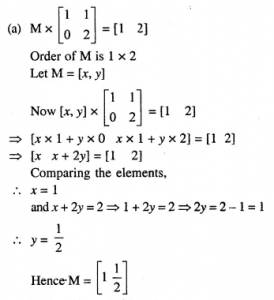

Question 18
If A= ……….and B=…..Find the value of X given That……….
Answer 18
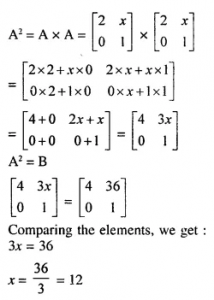
Question 19
If A=….., B=……. and C=……..Find AB-5C
Answer 19
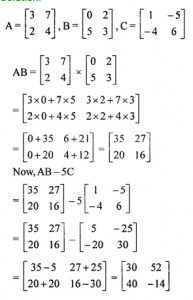
Question 20
If A and B are any two 2 x 2 matrices such that AB = BA = B and B is not a zero matrix, What can you say about the matrix A?
Answer 20
AB = BA = B
But it is possible, when A = 0 or B = 0
But B is not a zero matrix (given)
A is a zero matrix or A is an identity matrix
Question 21
Given A=………, B=…….. and ThatAB=A+B,Find the value of a,b and c.
Answer 21
Question 22
If p=…..and Q=…. , then compute:
…………..true for matrix algebra?
Answer 22
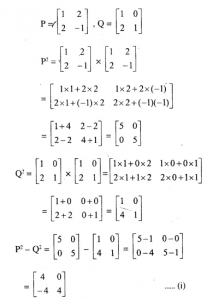

Questions 23
Given the Matrices A=………B=…. and C=……..
find (i)ABC 9ii)ACB state whether ABC=ACB
Answer-23

Question 24
If A=…,B=….and C=………find each of following if they are equal
(I) CA+B (ii) A+CB
Answer 24
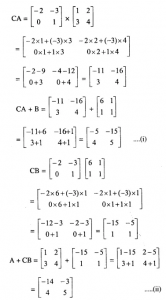
From (i) and (II) we can say say that CA+B not equal A+CB
Question 25
If A= ….. and B=……Find the matrix of x such that AX=B
Answer 25
Question 26
If A=…..Find (A-2I)(A-3I)
Answer 26

Question 27
If A=…. Find:…..Transpose of Matrix A
Answer 27

Question 28
If M=…..Show That…..Unit Matix
Answer 28
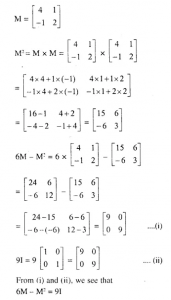
Question 29
If p=…..and Q=…… find x and y such that PQ=nul matrix.
Answer 29
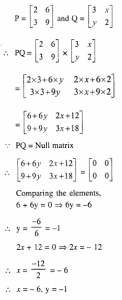
Question 30
Evaluate…………….
Answer 30
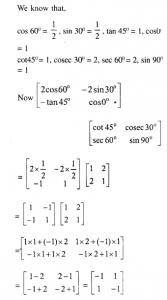
Question 31.
State, with reason, whether the following are true or false. A, B and C are matrices of order 2 x 2.
(i) A + B = B + A
(ii) A – B = B – A
(iii) (B . C). A = B . (C . A)
………………………
(vii) A² – B² = (A + B) (A – B)
(viii) (A – B)² = A² – 2 A . B + B²
Answer 31
(i) True : Because addition of matrices is commutative.
(ii) False : Subtraction of matrices is not commutative.
(iii) True : Multiplication of matrices is associative.
(iv) True: Multiplication of matrices is distributive over addition.
(v) True : As given above in (iv)
(vi) True : As given above in (iv)
(vii) False : Laws of algebra for factorization and expansion are not applicable to matrices.
(viii) False, As given above in (vii)
Exercise 9 (D),Chapter-9 Matrices Concise Maths Solutions Selina Publishers
Question 1.
Find x and y, if:………….
Answer 1

Question 2.
Find x and y, if :…….
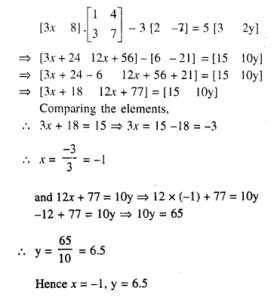
Question 3
If …….find x and y,if (i)…..(ii)…
Answer 3
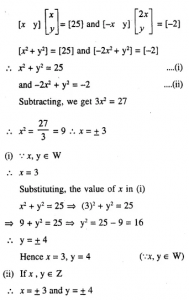
Question 4
Given….X=….Write:
(i) the order of the matrix X
(ii) the matrix X.
Answer 4

Question 5.
Evaluate…….
Answer 5

Question 6
if A=….,B=…. and 3A x M = 2B, Find Matrix M
Answer 6

Question 7
If………..find value of a, b, and c.
Answer 7

Question 8
if A =……… and B =………
(i) A (BA)
(ii) (AB)
Answer 8 part (i)

Answer 8 part (ii)
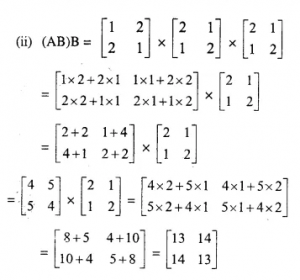
Question 9
Find x and y, if………
Answer 9

Question 10
If Matrix X = …… and 2X – 3Y=……..find the matrix X and Matrix Y
Answer 10
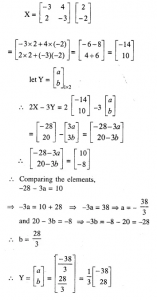
Question 11
Given A=…….B=…. and C=….find Matrix X such that A+X = 2B+C (2005)
Answer 11
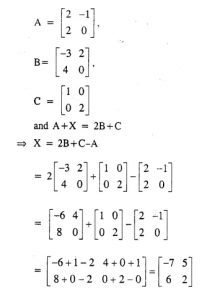
Question 12
Find the Value of x given that ………(2005)
Answer 12
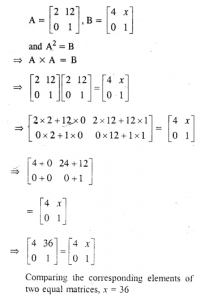
Question 13
If …., and I is identity matrix of the same order and At is the transpose of matrix A, find At .B + BI
Answer 13
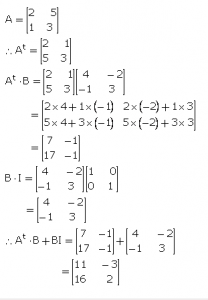
Question 14
Given A = …. B=…. and C=…..find matrix X such that A+2X = 2B+C
Answer 14
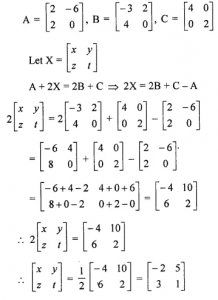
Question 15
Let…………. Find A2 – A + BC.
Answer 15

Question 16
Let A =……… Find A2 + AB + B2.
Answer 16
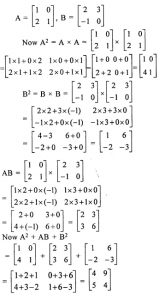
Question 17
If …………and 3A – 2C = 6B, find the values of a, b and c.
Answer 17

Question 18
Given A =……………
Find the values of p and q.
Answer 18

By comparing,
-2q = -8 q = 4
And p = 8
Question 19
Given A = …………. Find AB + 2C – 4D.
Answer 19
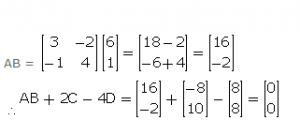
Question 20
Evaluate:…………
Answer 20
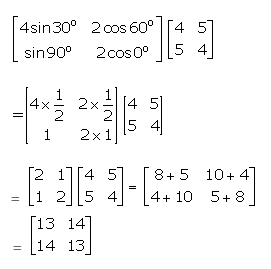
Question 21
If A=……. I =…… find ……..AxA.-5A+7I
Answer 21

Question 22
Given A = ……… And I = ……And …..Find M
Answer 22

Question 23
A=……and B=…….if AX = B (2016)
(i) Write the order of matrix X.
(ii) Find the matrix ‘X’
Answer 23
(i) Let the order of matrix X = m × n
Order of matrix A = 2 × 2
Order of matrix B = 2 × 1
Now, AX = B
∴ m = 2 and n = 1
Thus, order of matrix X = m × n = 2 × 1

Multiplying (1) by 2, we get
4x + 2y = 8 ….(3)
Subtracting (2) from (3), we get
3x = 3
⇒ x = 1
Substituting the value of x in (1), we get
2(1) + y = 4
⇒ 2 + y = 4
⇒ y = 2
Hence The Matrix X = x = 1 and y=2
Question 24
If A = ……..Find the matrix C where C is a 2 by 2 matrix. (2017)
Answer 24

Question 25
Given matrix B=…… Find the matrix X if, X = B2 – 4B. Hence, solve for a and b given ………..(2017)
Answer 25
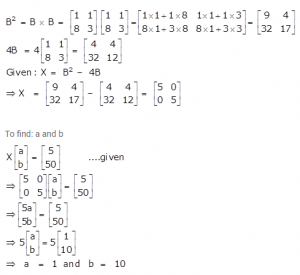
—: End of of Matrices Selina Concise Solutions Chapter- 9 :—
Return to :- Concise Selina Maths Solutions for ICSE Class-10
Thanks
Please share with your friends