ML Aggarwal Rectilinear Figures MCQs Class 9 ICSE Maths Solutions Ch-13. Step by Step Solutions of MCQs on Rectilinear Figures of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Rectilinear Figures MCQs Class 9 ICSE Maths Solutions Ch-13
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-13 | Rectilinear Figures |
| Topics | Solution of MCQs Questions |
| Academic Session | 2024-2025 |
MCQs on Rectilinear Figures
ML Aggarwal Rectilinear Figures Class 9 ICSE Maths Solutions Ch-13
Question 1. Three angles of a quadrilateral are 75°, 90° and 75°. The fourth angle is
(a) 90°
(b) 95°
(c) 105°
(d) 120°
Answer : (d) 120° is correct
Hint: Sum of 4 angles of a quadrilateral = 360° Sum of three angles = 75° + 90° + 75° = 240° Fourth angle = 360° – 240° = 120°
Question 2. A quadrilateral ABCD is a trapezium if
(a) AB = DC
(b) AD = BC
(c) ∠A + ∠C = 180°
(d) ∠B + ∠C = 180°
Answer : (d) ∠B + ∠C = 180° is correct
Hint: A quadrilateral ABCD is a trapezium if ∠B + ∠C= 180°
(Sum of co-interior angles)
Question 3. If PQRS is a parallelogram, then ∠Q – ∠S is equal to
(a) 90°
(b) 120°
(c) 0°
(d) 180°
Answer : (c) 0° is correct
Hint: PQRS is a parallelogram ∠Q – ∠S = 0
(∵ Opposite angles of a parallelogram, are equal)
Question 4. A diagonal of a rectangle is inclined to one side of the rectangle at 25°. The acute angle between the diagonals is
(a) 55°
(b) 50°
(c) 40°
(d) 25°
Answer : (b) 50° is correct
Hint: In a rectangle a diagonal is inclined to one side of the rectangle is 25°
In ΔOCD,
∠ODC + ∠OCD + ∠COD = 180°
⇒ 25° + 25° + ∠COD = 180°
⇒ ∠COD = 130°
Acute angle i.e. ∠DOA between the diagonals
= 180° – ∠DOC
= 180° – 130° = 50°
Question 5. ABCD is a rhombus such that ∠ACB = 40°. Then ∠ADB is
(a) 40°
(b) 45°
(c) 50°
(d) 60°
Answer : (c) 50° is correct
Hint: According to the question,
ABCD is a rhombus
∠ACB = 40°
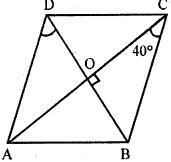
∵ ∠ACB = 40°
⇒ ∠OCB = 40°
∵ AD ∥ BC
⇒ ∠DAC = ∠BCA = 40° [Alternate interior angles]
⇒ ∠DAO = 40° Since, diagonals of a rhombus are perpendicular to each other
∠AOD = 90°
Sum of all angles of a triangle = 180°
⇒ ∠AOD + ∠ADO + ∠DAO = 180°
⇒ 90° + ∠ADO + 40° = 180°
⇒ 130° + ∠ADO = 180° ⇒ ∠ADO = 180° – 130°
⇒ ∠ADO = 50°
⇒ ∠ADB = 50°
Hence, ∠ADB = 50°
Question 6. The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠D AC = 32° and ∠AOB = 70°, then ∠DBC is equal to
(a) 24°
(b) 86°
(c) 38°
(d) 32°
Answer : (c) 38° is correct
Hint: ∠AOB = 70°, ∠DAC = 32°

∵ AD ∥ BC and AC is transversal
∴ ∠ACB = 32°
∠AOB + ∠BOC = 180°
⇒ 70° + ∠BOC = 180°
⇒ ∠BOC = 180° – 70°
⇒ ∠BOC = 110°
Sum of all angles of a triangle = 180°
⇒ ∠BOC + ∠BCO + ∠OBC = 180°
⇒ 110° + 32°+ ∠OBC = 180°
⇒ 142°+ ∠OBC = 180°
⇒ ∠OBC = 180° – 142°
⇒ ∠OBC = 38°
Hence, ∠DBC = 38°
Question 7. If the diagonals of a square ABCD intersect each other at O, then ∆OAB is
(a) an equilateral triangle
(b) a right angled but not an isosceles triangle
(c) an isosceles but not right angled triangle
(d) an isosceles right angled triangle
Answer : (d) an isosceles right angled triangle is correct
Question 8. If the diagonals of a quadrilateral PQRS bisect each other, then the quadrilateral PQRS must be a
(a) parallelogram
(b) rhombus
(c) rectangle
(d) square
Answer : (a) parallelogram is correct
Hint: Diagonals of a quadrilateral PQRS bisect each other, then quadrilateral must be a parallelogram.
(∵ A rhombus, rectangle and square are also parallelogram)
Question 9. If the diagonals of a quadrilateral PQRS bisect each other at right angles, then the quadrilateral PQRS must be a
(a) parallelogram
(b) rectangle
(c) rhombus
(d) square
Answer : (c) rhombus is correct
Diagonals of quadrilateral PQRS bisect each other at right angles, then quadrilateral PQRS [ must be a rhombus.
(∵ Square is also a rhombus with each angle equal to 90°)
Question 10. Which of the following statement is true for a parallelogram?
(a) Its diagonals are equal.
(b) Its diagonals are perpendicular to each other.
(c) The diagonals divide the parallelogram into four congruent triangles.
(d) The diagonals bisect each other.
Answer : (d) The diagonals bisect each other is correct
For a parallelogram an the statement ‘The diagonals bisect each other’ is true.
Question 11. Which of the following is not true for a parallelogram?
(a) opposite sides are equal
(b) opposite angles are equal
(c) opposite angles are bisected by the diagonals
(d) diagonals bisect each other
Answer : (c) opposite angles are bisected by the diagonals is correct
The statement that in a parallelogram, .the opposite angles are bisected by the diagonals, is not true in each case.
Question 12. A quadrilateral in which the diagonals are equal and bisect each other at right angles is a
(a) rectangle which is not a square
(b) rhombus which is not a square
(c) kite which is not a square
(d) square
Answer : (d) square is correct
Hint: In a quadrilateral, if diagonals are equal and bisect each other at right angles, is a square.
— : End of ML Aggarwal Rectilinear Figures MCQs Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends


