ML Aggarwal Algebraic Expression and Identities Exe-10.4 Class 8 ICSE Ch-10 Maths Solutions. We Provide Step by Step Answer of Exe-10.4 Questions for Algebraic Expression and Identities as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Algebraic Expression and Identities Exe-10.4 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-10 | Algebraic Expression and Identities |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-10.4 Questions |
| Edition | 2023-2024 |
Algebraic Expression and Identities Exe-10.4
ML Aggarwal Class 8 ICSE Maths Solutions
Page-180
Question 1. Divide:
(i) – 39pq2r5 by – 24p3q3r
(ii) –3⁄4a2b3 by 6⁄7 a3b2
Answer:
(i) – 39pq2r5 (÷) – 24p3q3r
= – 39pq2r5/ – 24p3q3r
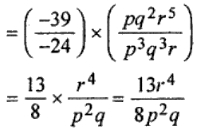
(ii) –3⁄4a2b3 by 6⁄7 a3b2
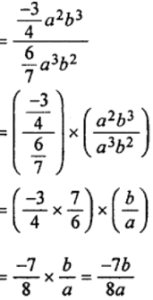
Algebraic Expression and Identities Exe-10.4
ML Aggarwal Class 8 ICSE Maths Solutions
Page-181
Question 2. Divide:
(i) 9x4 – 8x3 – 12x + 3 by 3x
(ii) 14p2q3 – 32p3q2 + 15pq2 – 22p + 18q by – 2p2q.
Answer:
(i) 9x4 – 8x3 – 12x + 3 by 3x
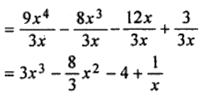
(ii) 14p2q3 – 32p3q2 + 15pq2 – 22p + 18q by – 2p2q.

Question 3. Divide:
(i) 6x2 + 13x + 5 by 2x + 1
(ii) 1 + y3 by 1 + y
(iii) 5 + x – 2x2 by x + 1
(iv) x3 – 6x2 + 12x – 8 by x – 2
Answer:
(i) 6x2 + 13x + 5 by 2x + 1
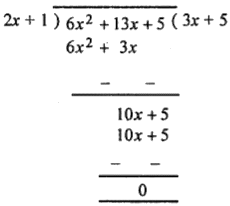
∴ Quotient = 3x + 5 and remainder = 0
(ii) 1 + y3 by 1 + y
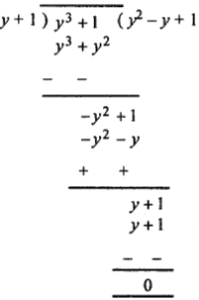
∴ Quotient = y2 – y + 1 and remainder = 0
(iii) 5 + x – 2x2 by x + 1
On arranging the terms of dividend in descending order of powers of x and then dividing,
– 2x2 + x + 5 ÷ x + 1

∴ Quotient = – 2x + 3 and remainder = 2
(iv) x3 – 6x2 + 12x – 8 by x – 2
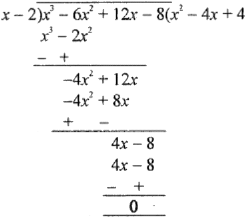
∴ Quotient = x2 – 4x + 4 and remainder = 0
Question 4. Divide:
(i) 6x3 + x2 – 26x – 25 by 3x – 7
(ii) m3 – 6m2 + 7 by m – 1
Answer:
(i) 6x3 + x2 – 26x – 25 by 3x – 7
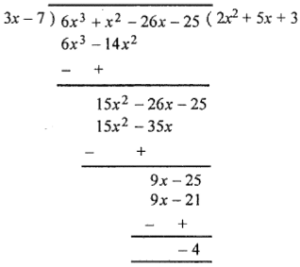
∴ Quotient = 2x2 + 5x + 3 and remainder = – 4
(ii) m3 – 6m2 + 7 by m – 1

∴ Quotient = m2 – 5m – 5 and remainder = 2.
Question 5. Divide:
(i) a3 + 2a2 + 2a + 1 by a2 + a + 1
(ii) 12x3 – 17x2 + 26x – 18 by 3x2 – 2x + 5
Answer:
(i) a3 + 2a2 + 2a + 1 by + a2 + a + 1

∴ Quotient = a + 1 and remainder = 0.
(ii) 12x3 – 17x2 + 26x – 18 by 3x2 – 2x + 5

∴ Quotient = 4x – 3 and remainder = -3
Question 6. If the area of a rectangle is 8x2 – 45y2 + 18xy and one of its sides is 4x + 15y, find the length of the adjacent side.
Answer:
Area of rectangle = 8x2 – 45y2 + 18xy
And, one side = 4x + 15y
∴ Second (adjacent) side = Area of rectangle/ One side
= 8x2 – 45y2 + 18xy ÷ 4x + 15y
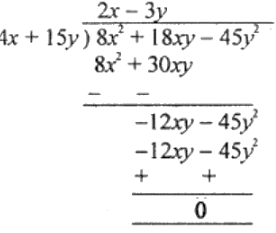
Thus, length of the adjacent side is 2x – 3y.
Question 7. What polynomial be subtracted from the polynomial x4 + 2x3 + x2 – 18x – 15 so that the resulting polynomial is exactly divisible by x2 – 1 – x.
Answer:
x4 + 2x3 + x2 – 18x – 15 by x2 – 1 – x.

Hence, Quotient =x2 + 3x + 5 and Remainder = −10x − 10
— End of Algebraic Expression and Identities Exe-10.4 Class 8 ICSE Maths Solutions :–
Return to : – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks


