ML Aggarwal Cubes and Cube Roots Exe-4.2 Class 8 ICSE Ch-4 Maths Solutions. We Provide Step by Step Answer of Exe-4.2 Questions for Cubes and Cube Roots as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Cubes and Cube Roots Exe-4.2 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-4 | Cubes and Cube Roots |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-4.2 Questions |
| Edition | 2023-2024 |
Cubes and Cube Roots Exe-4.2
ML Aggarwal Class 8 ICSE Maths Solutions
Page-76
Question 1. Find the cube root of each of the following numbers by prime factorisation:
(i) 12167
(ii) 35937
(iii) 42875
(iv) 21952
(v) 373248
(vi) 32768
(vii) 262144
(viii) 157464
Answer :
(i) 12167
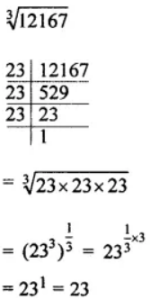
(ii) 35937

(iii) 42875

(iv) 21952

(v) 373248


(vi) 32768

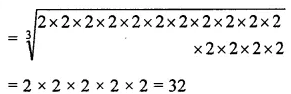
(vii) 262144

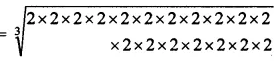
= 2 x 2 x 2 x 2 x 2 x 2 = 64
(viii) 157464

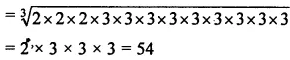
Question 2. Find the cube root of each of the following numbers:
(i) -250047
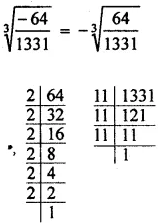
(ii) -64/1331
(iii) 4(17/27)
(iv) 5(1182/2197)
Answer :
(i) -250047
![]()

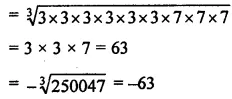
(ii) -64/1331
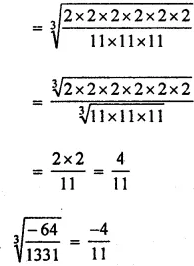
(iii) 4(17/27)

(iv) 5(1182/2197)
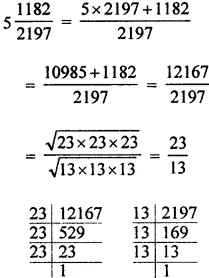
Question 3. Evaluate the following:
![]()
![]()
Answer :
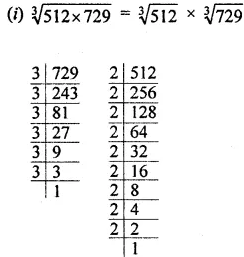
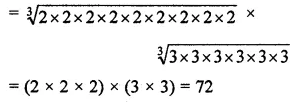
![]()

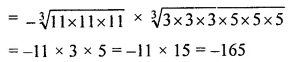
Question 4. Find the cube root of the following decimal numbers:
(i) 0.003375
(ii) 19.683
Answer :
(i) 0.003375

(ii) 19.683
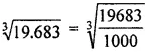

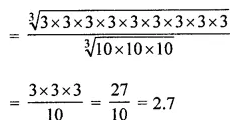
Question 5. Evaluate:
![]()
Answer :
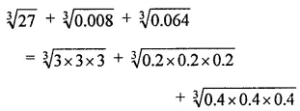
= 3 + 0.2 + 0.4 = 3.6
Question 6. Multiply 6561 by the smallest number so that product is a perfect cube. Also find the cube root of the product.
Answer :
6561 = 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3

6561 = (3 × 3 × 3) × (3 × 3 × 3) × 3 × 3After grouping of the equal factors in 3’s, it’s seen that 3 × 3 is left ungrouped in 3’s.
In order to complete it in triplet, we should multiply it by 3.
Therefore, required smallest number = 3
and cube root of the product = 3 × 3 × 3 = 27
Question 7. Divide the number 8748 by the smallest number so that the quotient is a perfect cube. Also, find the cube root of the quotient.
Answer :
8748 = 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3 × 3

Grouping of the equal factor in 3’s, it’s seen that 2 × 2 × 3 is left without grouping.
8748 = 2 × 2 × 3 × (3 × 3 × 3) × (3 × 3 × 3)
Therefore, on dividing the number 8748 by 12, we get 729
And, the cube root of 729 is 3 × 3 = 9.
Question 8. The volume of a cubical box is 21952 m3. Find the length of the side of the box.
Answer :
The volume of a cubical box is 21952 m2.


Question 9. Three numbers are in the ratio 3 : 4 : 5. If their product is 480, find the numbers.
Answer :
Three numbers are in the ratio 3:4:5 and their product = 480
Let’s assume the numbers to be 3x, 4x and 5x, then we have
3x × 4x × 5x = 480
⇒ 60 x3 = 480
⇒ x3 = 480/60 = 8 = (2)3
∴ x = 2
Hence, the number are 2 × 3, 2 × 4 and 2 × 5 = 6, 8 and 1
Question 10. Two numbers are in the ratio 4 : 5. If the difference of their cubes is 61, find the numbers.
Answer :
Two numbers are in the ratio = 4 : 5
Difference between their cubes = 61
Assume the numbers to be 4x and 5x
So, we have
(5x)3 – (4x)3 = 61
125x3 – 64x3 = 61
61x3 = 61
x3 = 1 = (1)3
∴ x = 1
4x = 4 × 1 = 4 and 5x = 5 × 1 = 5
Hence, the numbers are 4 and 5
Question 11. The difference of two perfect cubes is 387. If the cube root of the greater of two numbers is 8, find the cube root of the smaller number.
Answer :
The difference in two cubes = 387
And, the cube root of the greater number = 8
So, the greater number = (8)3 = 8 × 8 × 8 = 512
Therefore, the second number = 512 – 387 = 125
The cube root of 125 is
![]()
= 5
— : End of ML Aggarwal Cubes and Cube Roots Exe-4.2 Class 8 ICSE Maths Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks
Please Share with Your Friends


