ML Aggarwal Factorisation Ch-Test Class 10 ICSE Maths Solutions Ch-6 . We Provide Step by Step Answer of Ch-Test Questions for Factorisation as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Solutions of Quadratic Equations in one Variable Chapter-Test Questions for ICSE Class 10 Maths
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-6 | Factorisation |
| Writer / Book | Understanding |
| Topics | Solutions of Ch-Test |
| Academic Session | 2024-2025 |
ML Aggarwal Solutions for ICSE Class 10 Maths
(i) x – 2
(ii) x + 3
(iii) 2x + 1
Answer -1
(i) let x – 2 = 0, Then, x = 2
Now, substitute the value of x in f(x),
f(2) = 2(2)3 – 3(2)2 + 4(2) + 7
= 16 – 12 + 8 + 7
= 31 -12 = 19
Hence the remainder is 19
(ii) let x + 3 = 0 , Then, x = -3
substitute the value of x in f(x),
f(2) = 2(-3)3 – 3(-3)2 + 4(-3) + 7
= 2(-27) – 3(9) – 12 + 7
or – 54 – 27 – 12 + 7
or – 93 + 7
= – 86
Hence remainder is -86.
(iii) Let , 2x + 1 = 0, Then, 2x = -1
X = -½
substitute the value of x in f(x),
f (-½) = 2 (-½)3 – 3(-½)2 + 4 (-½) + 7
= 2(-1/8) – 3 (¼) + 4 (-½) + 7
or -¼ – ¾ – 2 + 7
= -1 – 2 + 7
= 4
Hence remainder is 4.
Question -2 When 2x3 – 9x2 + 10x – p is divided by (x + 1), the remainder is – 24.Find the value of p.
Answer -2
Let x + 1 = 0, Then, x = -1
Given, f(x) = 2x3 – 9x2 + 10x – p
substitute the value of x in f(x),
f(-1) = 2(-1)3 – 9(-1)2 + 10(-1) – p
= -2 – 9 – 10 + p
= -21 + p
given that, the remainder = – 24,
So, -21 + p = -24
p = – 24 + 21
p = -3
therefore value of p is 3.
Question -3 If (2x – 3) is a factor of 6x2 + x + a, find the value of a. With this value of a, factorise the given expression.
Answer -3
Let 2x – 3 = 0, Then, 2x = 3
X = 3/2, Given, f(x) = 6x2 + x + a
substitute the value of x in f(x),
f(3/2) = 6(3/2)2 + (3/2) + a
= 6(9/4) + (3/2) + a
= 3(9/2) + (3/2) + a
or 27/2 + 3/2 + a
= 30/2 + a
= 15 + a
(2x – 3) is a factor of 6x2 + x + a.
remainder is 0.
Then, 15 + a = 0
a = -15
Therefore, f(x) = 6x2 + x – 15
Dividing f(x) by 2x – 3 we get,
6x2 + x – 15 = (2x – 3) (3x + 5)
Question- 4 When 3x2 – 5x + p is divided by (x – 2), the remainder is 3. Find the value of p. Also factorise the polynomial 3x2 – 5x + p – 3.
Answer -4
Let x – 2 = 0, Then, x = 2
f(x) = 3x2 – 5x + p
substitute the value of x in f(x),
So, f(2) = 3(2)2 – 5(2) + p
= 3(4) – 10 + p
or 12 – 10 + p
= 2 + p
given that, remainder= 3.
, 2 + p = 3
p = 3 – 2
p = 1
Therefore, f(x) = 3x2 – 5x + 1
polynomial, 3x2 – 5x + p – 3
substitute the value of p
= 3x2 – 5x + 1 – 3
= 3x2 – 5x – 2
Now, by factorizing the polynomial 3x2 – 5x – 2,
now Dividing 3x2 – 5x – 2 by x – 2
= (x – 2) (3x + 1)
Question- 5 Prove that (5x + 4) is a factor of 5x3 + 4x2 – 5x – 4. Hence factorize the given polynomial completely.
Answer -5
Let (5x + 4) = 0
Then, 5x = -4
x = -4/5
Given, f(x) = 5x3 + 4x2 – 5x – 4
substitute the value of x in f(x),
So, f(-4/5) = 5(-4/5)3 + 4(-4/5)2 – 5(-4/5) – 4
= 5(-64/125) + 4 (16/25) + 4 – 4
= -64/25 + 64/25
= (-64 + 64)/25
= 0/25
= 0
Hence, (5x + 4) is a factor of 5x3 + 4x2 – 5x – 4.
So, dividing 5x3 + 4x2 – 5x – 4 by 5x + 4 we get,
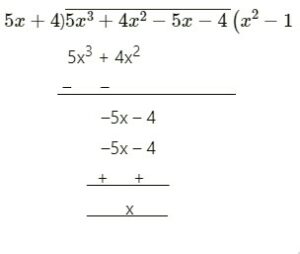
5x3 + 4x2 – 5x – 4 = (5x + 4) (x2 – 1)
= (5x + 4) (x2 – 12)
= (5x + 4) (x + 1) (x – 1)
Question- 6 Use factor theorem to factorise the following polynomials completely:
(i) 4x3 + 4x2 – 9x – 9
(ii) x3 – 19x – 30
Answer- 6
Let x = -1, Given, f(x) = 4x3 + 4x2 – 9x – 9
substitute the value of x in f(x),
f(-1) = 4(-1)3 + 4(-1)2 – 9(-1) – 9
= -4 + 4 + 9 – 9 , = 0
x + 1 is the factor of 4x3 + 4x2 – 9x – 9.
dividing 4x3 + 4x2 – 9x – 9 by x + 1
4x3 + 4x2 – 9x – 9 = (x + 1) (4x2 – 9)
= (x + 1) ((2x)2 – (3)2)
= (x + 1) (2x + 3) (2x – 3)
(ii) x3 – 19x – 30
Let x = -2, Given, f(x) = x3 – 19x – 30
substitute the value of x in f(x),
f(-1) = (-2)3 – 19(-2) – 30
= -8 + 38 – 30
= -38 + 38, = 0
, x + 2 is the factor of x3 – 19x – 30.
dividing x3 – 19x – 30 by x + 2,
x3 – 19x – 30 = (x + 2)(x2 – 2x – 15)
= (x + 2) (x2 – 5x + 3x – 15)
= (x + 2) (x – 5) (x + 3)
Question- 7 If x3 – 2x2 + px + q has a factor (x + 2) and leaves a remainder 9, when divided by (x + 1), find the values of p and q. With these values of p and q, factorize the given polynomial completely.
Answer- 7
Let x + 2 = 0, Then, x = -2
Now, substitute the value of x in f(x),
f(-2) = (-2)3 – 2(-2)2 + p(-2) + q
= -8 – 8 – 2p + q
= -16 – 2p + q
2p – q = – 16 … (i)
and in case — 2
Let x + 1 = 0, Then, x = -1
substitute the value of x in f(x),
f(-1) = (-1)3 – 2(-1)2 + p(-1) + q
= -1 – 2 –p + q
= – 3 – p + q
remainder = 9 Given,
-3 – p + q = 9
– p + q = 9 + 3
-p + q = 12 … (ii)
adding equation (i) and (ii)
(2p – q) + (-p + q) = – 16 + 12
2p – q – p + q = -4
P = -4
Putting value P = -4 in equation (ii) to find ‘b’.
– p + q = 12
-(-4) + q = 12
4 + q = 12
q = 12 – 4, q = 8
substituting the value of p and q in f(x)
= x3 – 2x2 – 4x + 8
Dividing f(x) by (x + 2)

x3 – 2x2 – 4x + 8 = (x + 2) (x2 – 4x + 4)
= (x + 2) (x2 – 2 × x (-2) + 22)
= (x + 2) (x – 2)2
Question -8 If (x + 3) and (x – 4) are factors of x3 + ax2 – bx + 24, find the values of a and b: With these values of a and b, factorise the given expression.
Answer -8
f(x) = x3 + ax2 – bx + 24
Let x + 3 = 0, then x = -3
Substituting the value of x in f(x)
f(–3) = (–3)3 + a(–3)2– b(–3) + 24,
= –27 + 9a + 3b + 24
= 9a + 3b – 3
∵ x + 3 is a factor,
∴ Remainder = 0,
∴ 9a + 3b – 3 = 0
⇒ 3a + b – 1 = 0 …(Dividing by 3)
⇒ 3a + b = 1 …(i)
Again Let x – 4 = 0,
then x = 4
Substituting the value of x in f(x)
f(x) = (4)2 + a(4)2 – b(4) + 24
= 64 + 16a – 4b + 24
= 16a – 4b + 88
∵ x – 4 is a factor
∴ Remainder = 0
16a – 4b + 88 = 0
⇒ 16a – 4b = – 88 …(Dividing by 4)
⇒ 4a – b = –22 …(ii)
Adding (i) and (ii)
7a = –21,
⇒ a = –3
Substituting the value of a in (i)
3(–3) + b = 1
⇒ –9 + b = 1
⇒ b = 1 + 9 = 10
∴ a = –3, b = 10
Now f(x) will be
f(x) = x3 – 3x2 – 10x + 24
∵ x + 3 and x – 4 are factors of f(x)
∴ Dividing f(x) by (x + 3)(x – 4)
or x2 – x – 12
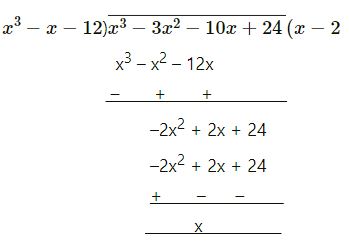
x3 – 3x2 – 10x + 24
= (x2 – x – 12)(x – 2)
= (x + 3)(x – 4)(x – 2).
Question -9 If (2x + 1) is a factor of both the expressions 2x2 – 5x + p and 2x2 + 5x + q, find the value of p and q. Hence find the other factors of both the polynomials.
Answer -9
Let 2x + 1 = 0
Then, 2x = -1 so x = -½
Given, p(x) = 2x2 – 5x + p
substitute the value of x in p(x),
p (-½) = 2 (-½)2 – 5(-½) + p
= 2(1/4) + 5/2 + p
or ½ + 5/2 + p
= 6/2 + p
= 3 + p
given that, (2x + 1) is a factor of both the expressions 2x2 – 5x + p
remainder is 0. Then, 3 + p = 0
p = – 3
Now = 2x2 + 5x + q
Substitute the value of x in q(x)
q (-½) = 2 (-½)2 + 5(-½) + q
= 2(1/4) – 5/2 + q
= ½ – 5/2 + q
or (1 – 5)/2 + q
= -4/2 + q
= q – 2
given that, (2x + 1) is a factor of both the expressions 2x2 + 5x + q
remainder is 0. so q – 2 = 0 then q = 2
Therefore, p = – 3 and q = 2
P(x) = 2x2 – 5x – 3
q(x) = 2x2 + 5x + 2
Then, divide p(x) by 2x + 1
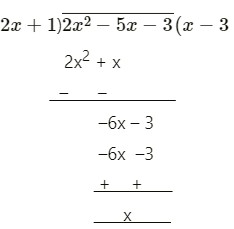
2x2 – 5x – 3 = (2x + 1) (x – 3)
divide q(x) by 2x + 1
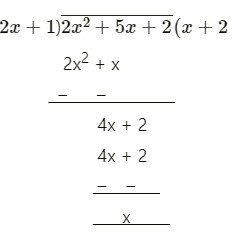
2x2 + 5x + 2 = (2x + 1) (x + 2)
Question-10 If a polynomial f(x)= X4-2x3-3x2-ax-b leaves reminder 5 and 19 when divided by (x-1) and (x+1) respectively, Find the values of a and b .Hence determined the reminder when f(x) is divided by (x-2).
Answer -10 Given that the equation
f(x) = x4 – 2x3 + 3x2 – ax +b
When f(x) is divided by (x+1) and (x-1) , the remainders are 19 and 5 respectively .
∴ f(-1) = 19 and f(1) = 5
(-1)4 – 2 (-1)3 + 3(-1)2 – a (-1) + b = 19
⇒ 1 +2 + 3 + a + b = 19
∴ a + b = 13 ——- (1)
According to given condition f(1) = 5
f(x) = x4 – 2x3 + 3x2 – ax
⇒ 14 – 2 3 + 3 2 – a (1) b = 5
⇒ 1 – 2 + 3 – a + b = 5
∴ b – a = 3 —— (2)
solving equations (1) and (2)
a = 5 and b = 8
Now substituting the values of a and b in f(x) , we get
∴ f(x) = x4 – 2x3 + 3x2 – 5x + 8
Also f(x) is divided by (x-2) so remainder will be f(2)
∴ f(x)= x4 – 2x3 + 3x2 – 5x + 8
⇒ f(2) = 16 – 16 + 3 × 4 – 5 × 2 + 8
= 12-10+8 = 10
Question -11 When a polynomial f(x) is divided by (x – 1), the remainder is 5 and when it is,, divided by (x – 2), the remainder is 7. Find – the remainder when it is divided by (x – 1) (x – 2).
Answer -11
When f(x) is divided by (x – 1),
Remainder = 5
Let x – 1 = 0
⇒ x = 1
∴ f(1) = 5
When divided by (x – 2),
Remainder = 7
Let x – 2 = 0
⇒ x = 2
∴ f(2) = 7
Let f(x) = (x – 1)(x – 2)q(x) + ax + b
Where q(x) is the quotient and ax + b is remainder
Putting x = 1, we get:
f(1) = (1 – 1)(1 – 2)q(1) + a x 1 + b
= 0 + a + b
= a + b
and x = 2, then
f(2) = (2 – 1)(2 – 2)q(2) + a x 2 + b
= 0 + 2a + b
= 2a + b
∴ a + b = 5 ….(i)
2a + b = 7 ….(ii)
Subtracting, we get
–a = – 2
⇒ a = 2
Substituting the value of a in (5)
2 + b = 5
⇒ b = 5 – 2 = 3
∴ a = 2, b = 3
∴ Remainder = ax + b
= 2x + 3.
— : End of ML Aggarwal Factorisation Ch-Test Class 10 ICSE Maths Solutions Ch-6 :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


