ML Aggarwal Mensuration Exe-18.4 Class 8 ICSE Ch-18 Maths Solutions. We Provide Step by Step Answer of Exe-18.4 Questions for Mensuration as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Mensuration Exe-18.4 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-18 | Mensuration |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-18.4 Questions |
| Edition | 2023-2024 |
Mensuration Exe-18.4
ML Aggarwal Class 8 ICSE Maths Solutions
Page-312
Question 1. The surface area of a cube is 384 cm2. Find
(i) the length of an edge
(ii) volume of the cube.
Answer:
Surface area of a cube = 384 cm2
(i) Surface area of cube = 6(side)2
Hence, edge (side) = √(surface area/6)
= √(384/6)
= √64
= 8 cm
(ii) Volume = (Edge)3 = (8)3 = 8 × 8 × 8 cm3 = 512 cm3
Question 2. Find the total surface area of a solid cylinder of radius 5 cm and height 10 cm. Leave your answer in terms of n.
Answer:
Radius of a solid cylinder (r) = 5 cm
Height (h) = 10 cm
Total surface area = 2πrh + 2πr2
= 2rπ(h + r)
= 2π × 5(10 + 5)
= π × 10 × 15 = 150π cm2
Question 3. An aquarium is in the form of a cuboid whose external measures are 70 cm × 28 cm × 35 cm. The base, side faces and back face are to be covered with coloured paper. Find the area of the paper needed.
Answer:
A cuboid shaped aquarium,
Length (l) = 70 cm
Breadth (b) = 28 cm
and height (h) = 35 cm
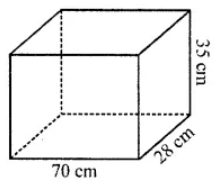
Area of base = 70 × 28 cm3 = 1960 cm3
Area of side face = (28 × 35) × 2 cm2 = 1960 cm2
Area of back face = 70 × 35 cm2 = 2450 cm
∴. Total area = 1960 + 1960 + 2450 = 6370 cm2
∴ Area of paper required = 6370 cm2
Question 4. The internal dimensions of rectangular hall are 15 m × 12 m × 4 m. There are 4 windows each of dimension 2 m × 1.5 m and 2 doors each of dimension 1.5 m × 2.5 m. Find the cost of white washing all four walls of the hall, if the cost of white washing is ₹5 per m2. What will be the cost of white washing if the ceiling of the hall is also white washed?
Answer:
Internal dimension of rectangular hall = 15m × 12 m × 4 m
Area of 4-walls = 2(l + b) × h
= 2(15 + 12) × 4
= 2 × 27 × 4 m2
= 216 m2
Area of 4 windows of size = 2 × 1.5 = 2 × 1.5 × 4 = 12 m2
Area of 2 door of size = 1.5 × 2.5 = 2 × 1.5 × 2.5 = 7.5 m2
∴ Area of remaining hall = 216 – (12 + 7.5) = 216 – 19.5 m2 = 196.5 m2
Area of ceiling = l × b = 15 × 12= 180 m2
Cost of white washing the walls at the rate of ₹5 per m2
= 196.5 × 5 = ₹982.50
Area of ceiling = l × b = 15 × 12= 180 m2
Cost of white washing = 180 × 5 = ₹900
∴ Total cost = ₹982.50 + 900.00 = ₹1882.50
Question 5. A swimming pool is 50 m in length, 30 m in breadth and 2·5 m in depth. Find the cost of cementing its floor and walls at the rate of ₹27 per square metre.
Answer:
Length of swimming pool = 50 m
Breadth of swimming pool = 30 m
Depth (Height) of swimming pool = 2·5 m
Area of floor = 50 × 30 = 1500 m2
Area of four walls = 2 (50 + 30) × 2·5 = 160 × 2·5 = 400 m2
Area to be cemented = 1500 m2 + 400 m2 = 1900 m2
Cost of cementing 1m2 = ₹27
Cost of cementing 1900m2 = ₹27 × 1900 = ₹51300
Question 6. The floor of a rectangular hall has a perimeter 236 m. Its height is 4·5 m. Find the cost of painting its four walls (doors and windows be ignored) at the rate of Rs. 8.40 per square metre.
Answer:
Perimeter of Hall = 236 m.
Height = 4·5 m
Perimeter = 2 (l + b) = 236 m
Area of four walls = 2 (l + b) × h = 236 × 4·5 = 1062 m2
Cost of painting 1 m2 = ₹8·40
Cost of painting 1062 m2 = ₹8·40 × 1062 = ₹8920·80
Question 7. A cuboidal fish tank has a length of 30 cm, a breadth of 20 cm and a height of 20 cm. The tank is placed on a horizontal table and it is three-quarters full of water. Find the area of the tank which is in contact with water.
Answer:
Length of tank = 30 cm
Breadth of tank = 20 cm
Height of tank = 20 cm
As the tank is three-quarters full of water
∴ Height of water in the tank = = 15 cm
Area of the tank in contact with the water = Area of floor of Tank
+ Area of 4 walls upto 15 cm
= 30 × 20 + 2 (30 + 20) × 15
= 600 + 2 × 50 × 15
= 600 + 1500 = 2100 cm2
Question 8. The volume of a cuboid is 448 cm3. Its height is 7 cm and the base is a square. Find
(i) a side of the square base
(ii) surface area of the cuboid.
Answer:
Volume of a cuboid = 448 cm3
Height = 7 cm
∴ Area of base = 448/7 = 64 cm2
∵ Base is a square.
(i) ∴ Side of square base = √64 = 8 cm
(ii) Surface area of the cuboid = 2 [lb + bh + hl]
= 2[8 × 8 + 8 × 7 + 7 × 8] cm2
= 2[64 + 56 + 56]
= 2 × 176 = 352 cm2
(ML Aggarwal Mensuration Exe-18.4 Class 8 ICSE Maths)
Question 9. The length, breadth and height of a rectangular solid are in the ratio 5 : 4 : 2. If its total surface area is 1216 cm2, find the volume of the solid.
Answer:
Ratio in length, breadth and height of a rectangular solid = 5 : 4 : 2
Total surface area =1216 cm2
Let Length = 5x,
Breadth = 4x
and height = 2x
Total surface area = 2[5x × 4x + 4x × 2x + 2x × 5x]
= 2[20x2 + 8x2 + 10x2 ]
= 2 × 38x2 = 76x2
∴ 94x2 = 1216
⇒ x2 = 1216/76 = 16 = (4)2
∴ x = 4
∴ Length = 5 × 4 = 20 cm
Breadth = 4 × 4 = 16 cm
Height = 2 × 4 = 8 cm
and volume = lbh = 20 × 16 × 8 = 2560 cm3
Question 10. A rectangular room is 6 m long, 5 m wide and 3·5 m high. It has 2 doors of size 1·1 m by 2 m and 3 windows of size 1·5 m by 1·4 m. Find the cost of whitewashing the walls and the ceiling of the room at the rate of ₹5·30 per square metre.
Answer:
Length of room = 6 m
Breadth of room = 5 m
Height of room = 3·5 m
Area of four walls = 2 (l + b) × h
= 2 (6 + 5) × 3·5 = 77 m2
Area of 2 doors and 3 windows
= (2 × 1·1 × 2 + 3 × 1·5 × 1·4)
= (44 + 6·3) m2 = 10·7 m2
Area of ceiling = l × b = 6 × 5 = 30 m2
Total area for white washing
= (77 – 10·7 + 30) m2 = 96·3 m2
Cost of white washing = ₹(96·3 × 5·30) = ₹510·39
Question 11. A cuboidal block of metal has dimensions 36 cm by 32 cm by 0·25 m. It is melted and recast into cubes with an edge of 4 cm.
(i) How many such cubes can be made?
(ii) What is the cost of silver coating the surfaces of the cubes at the rate of ₹0·75 per square centimetre?
Answer:
(i) Length of cuboid = 36 cm
Breadth of cuboid = 32 cm
Height of cuboid = 0·25 × 100 = 25 cm
Volume of cubiod = lbh = (36 × 32 × 25) cm3 = 28800 cm3.
Volume of cube = (side)2 = (4)2 = 64 cm2
Number of cubes recasting from cubiod = 28800/64 = 450
(ii) Surface area of 1 cube = 6 × a2 = 6 × 16 = 96 cm2
Surface area of 450 cubes = 96 × 450 = 43200 cm2
Cost of silver coating on cubes = ₹0·75 × 43200 = ₹32400
Mensuration Exe-18.4
ML Aggarwal Class 8 ICSE Maths Solutions
Page-313
Question 12. Three cubes of silver with edges 3 cm, 4 cm and 5 cm are melted and recast into a single cube, find the cost of coating the surface of the new cube with gold at the rate of ₹3·50 per square centimetre?
Answer:
Let a cm be the edge of new cube
∴ According to question,
a3 = 33 + 43 + 53 = 27 + 64 + 125 = 216 cm3
a = 3√216
⇒ a = 6 cm.
Surface area of new cube = 6 × (side)2 = 6 × (6)2 = 216 cm2
Cost of coating the surface of new cube = ₹3·50 × 216 = ₹156
Question 13. The curved surface area of a hollow cylinder is 4375 cm2, it is cut along its height and formed a rectangular sheet of width 35 cm. Find the perimeter of the rectangular sheet.
Answer:
Curved surface area of a hollow cylinder = 4375 cm2
By cutting it from the height,
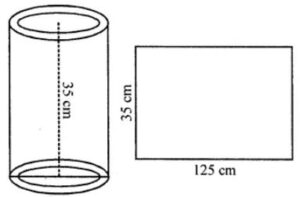
It becomes a rectangular sheet whose width = 35 cm
So, the height of cylinder = 35 cm
And, length of sheet = Area/Height
= 4375/35
= 125 cm
Perimeter of the sheet = 2(l + b)
= 2 × (125 + 35)
= 2 × 160
= 320 cm
Question 14. A road roller has a diameter 0.7 m and its width is 1.2 m. Find the least number of revolutions that the roller must take in order to level a playground of size 120 m × 44 m.
Answer:
Diameter of a road roller = 0.7 m = 70 cm
So, radius (r) = 70/2 cm = 35 cm = 35/100 m
and width (h) = 1.2 m
Now,
Curved surface area = 2πrh
= (2 × 22/7 × 35/100 × 1.2) m2
= 264/100 m2
Area of playground = 120 m × 44 m
= 120 × 44 m2
= 5280 m2
Hence, the number of revolution made by the road roller = (5280/264) × 100
= 2000 revolutions
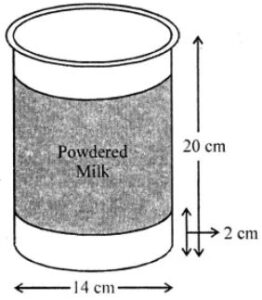
Question 15. A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label?
Answer:
Diameter of cylindrical container = 14 cm
∴ Radius (r) = 14/2 = 7 cm
and height (h) = 20 cm
Width of lable = 2 0 – (2 + 2) cm = 20 – 4 = 16 cm
∴ Area of lable = 2πrh = 2 × 22/7 × 7 × 16 = 704 cm2
(ML Aggarwal Mensuration Exe-18.4 Class 8 ICSE Maths)
Question 16. The sum of the radius and height of a cylinder is 37 cm and the total surface area of the cylinder is 1628 cm2. Find the height and the volume of the cylinder.
Answer:
Sum of height and radius of a cylinder = 37 cm
Total surface area = 1628 cm2
Let’s consider the radius to be r
Then, height = (37 – r) cm
Total surface area = 2π(h + r)
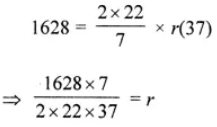
⇒ r = 7 cm
Height = 37 – 7 = 30 cm
Volume = πr2h
= (22/7) × 7 × 7 × 30 cm3
= 4620 cm3
Question 17. The ratio between the curved surface and total surface of a cylinder is 1 : 2. Find the volume of the cylinder, given that its total surface area is 616 cm3.
Answer:
Given that ratio between curved surface and total surface area of a cylinder = 1 : 2
Total surface area = 616 cm2
So, curved surface area = 616/2 = 308 cm2
Area of two circular faces = 616 – 308 = 308 cm2
Area of one circular face = 308/2 = 154 cm2
Now, let’s consider the radius to be r
πr2 = 154
(22/7) × r2 = 154
r2 = (154 × 7)/ 22 = 49
⇒ r = 49 = √7 cm
the volume = πr2h = (22/7) × 7 × 7 × 7 = 1078 cm2
Question 18. The given figure shown a metal pipe 77 cm long. The inner diameter of cross section is 4 cm and the outer one is 4.4 cm. Find its
(i) inner curved surface area
(ii) outer curved surface area
(iii) total surface area.
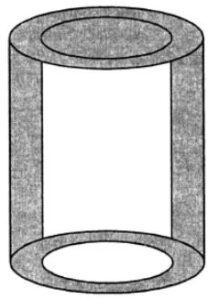
Answer:
Length of metal pipe (h) = 77 cm
Inner diameter = 4 cm
and outer diameter = 4.4 cm
So, inner radius (r) = 4/2 = 2 cm
And outer radius (R) = 4.4/2 = 2.2 cm
(i) Inner curved surface area = 2πrh
= 2 × 22/7 × 2 × 77 cm2
= 968 cm2
(ii) Outer surface area = 2πRH
= 2 × 22/7 × 2.2 × 77 cm2
= 1064.8 cm2
(iii) Surface area of upper and lower rings = 2[πR2 – πr2]
= 2 × 22/7 (2.22 – 22) cm2
= 44/7 × 4.2 × 0.2
= 5.28 cm2
Total surface area = (968 + 1064.8 + 5.28) cm2 = 2038.08 cm2
— End of Mensuration Exe-18.4 Class 8 ICSE Maths Solutions :–
Return to : – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks


