ML Aggarwal Ratio and Proportion Ch-Test Class 10 ICSE Maths Solutions Ch-7. We Provide Step by Step Answer of Ch-Test Questions for Ratio and Proportion as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Ratio and Proportion Ch-Test Class 10 ICSE Maths Solutions Ch-7
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-7 | Ratio and Proportion |
| Writer / Book | Understanding |
| Topics | Solutions of Ch-Test |
| Academic Session | 2024-2025 |
Ratio and Proportion, Ch-Test Questions
ML Aggarwal Class 10 ICSE Maths Solutions Ch-7
Question-1 Find the compound ratio of:
(a + b)2 : (a – b )2 ,
(a2 – b2) : (a2 + b2),
(a4 – b4) : (a + b)4
Answer -1
(a + b)2 : (a – b)2 ,
(a2 – b2) : (a2 + b2),
(a4 – b4) : (a + b)4
= {(a + b)2}/{(a – b)2} × (a2 – b2)/(a2 + b2) × (a4 – b4)/{(a + b)4}
= {(a + b)2/(a – b)2 } × {(a + b)(a – b)/(a2 + b2)} × {(a2 + b2)(a + b)(a – b)}/(a + b)4
= 1/1 , = 1 : 1
Question -2 If (7 p + 3 q) : (3 p – 2 q) = 43 : 2 find p : q
Answer -2
(7p + 3q) : (3p – 2q) = 43 : 2
⇒ (7p + 3q)/(3p – 2q) = 43/2
⇒ 129 p – 86q = 14p + 6q
⇒ 129p – 14p = 6q + 86q
⇒ 115p = 92q
⇒ p/q = 92/115 = 4/5
∴ p : q = 4 : 5
Question -3 If a : b = 3 : 5, find (3a + 5b): (7a – 2b).
Answer -3
a : b = 3 : 5
⇒ a/b = 3/5
⇒ 3a + 5n : 7a – 2b
Dividing each term by b
3.a/b + 5 : 3.a/b – 2
⇒ 3 × 3/5 + 5 : 7 × 3/5 – 2
or (9/5 + 5) : (21/5 – 2)
⇒ (9 + 25)/5 : (21 – 10)/5
or 34/5 : 11/5
= 34 : 11
Question -4 The ratio of the shorter sides of a right angled triangle is 5 : 12. If the perimeter of the triangle is 360 cm, find the length of the longest side.
Answer -4 Let the two shorter sides of a right-angled triangle be 5x and 12x.
Third (longest side)
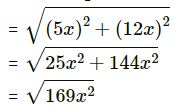
= 13x
But 5x + 12x + 13x = 360 cm
⇒ 30x = 360
⇒ x = 360/10 = 12
∴ Length of the longest side = 13x
= 13 × 12 cm
= 156 cm
Question- 5 The ratio of the pocket money saved by Lokesh and his sister is 5 : 6. If the sister saves Rs 30 more, how much more the brother should save in order to keep the ratio of their savings unchanged?
Answer- 5 Let the savings of Lokesh and his sister are 5x and 6x.
And the Lokesh should save Rs y more. Now, according to the problem,
⇒ (5x + y)/(6x + 30) = 5/6
or 30x + 6y = 30x + 150
⇒ 30x + 6y – 30x = 150
or 6y = 150
∴ y = 150/6
= 25
Hence, Lokesh should save ₹ 25 more
Ratio and Proportion, Ch-Test Questions
ML Aggarwal Class 10 ICSE Maths Solutions Ch-7
Page-136
Question- 6 In an examination, the number of those who passed and the number of those who failed were in the ratio of 3 : 1. Had 8 more appeared, and 6 less passed, the ratio of passed to failures would have been 2 : 1. Find the number of candidates who appeared.
Answer -6
Let number of passed = 3 x
and failed = x
Total candidates appeared = 3x + x = 4x.
In second case
No. of candidates appeared = 4 x + 8
and No. of passed = 3 x – 6
and failed = 4x + 8 – 3x + 6 = x + 14
then ratio will be = 2 : 1
Now according to the condition
(3x – 6)/(x + 14) = 2/1
⇒ 3x – 6 = 2x + 28
⇒ 3x – 2x = 28 + 6
⇒ x = 34
∴ No. of candidates appeared = 4x
= 4 × 34
= 136
Question- 7 What number must be added to each of the numbers 15, 17, 34 and 38 to make them proportional ?
Answer -7
Let x be added to each number, then numbers will be
15 + x, 17 + x, 34 + x, and 38 + x.
Now according to the condition
(15 + x)/(17 + x) = (34 + x)/(38 + x)
⇒ (15 + x)(38 + x) = (34 + x)(17 + x)
⇒ 570 + 53x + x2 = 578 + 51x + x2
or x2 + 53x – x2 – 51x = 578 – 570
⇒ 2x = 8
⇒ x = 4
∴ 4 is to be added.
Question- 8 If (a + 2 b + c), (a – c) and (a – 2 b + c) are in continued proportion, prove that b is the mean proportional between a and c.
Answer -8
(a + 2b + c), (a – c) and (a – 2b + c) are in continued proportion
⇒ (a + 2b + c)/(a – c) = (a – c)/(a – 2b + c)
∴ (a + 2b + c)/(a – c) = (a – c)/(a – 2b + c)
⇒ (a + 2b + c)(a – 2b + c) = (a – c)2
⇒ a2 – 2ab + ac + 2ab – 4b2 + 2bc + ac – 2bc + c2
= a2 – 2ac + c2
⇒ a2 – 2ab + ac + 2ab – 4b2 + 2bc + ac – 2bc + c2 – a2 + 2ac – c2 = 0
⇒ 4ac – 4b2 = 0
⇒ ac – b2 = 0
⇒ b2 = ac
Hence b is the mean proportional between a and c.
Question -9 If 2, 6, p, 54 and q are in continued proportion, find the values of p and q.
Answer -9
2, 6, p, 54 and q are in continued proportional then
⇒ 2/6 = 6/p = p/54 = 54/q
(i) ∵ 2/6 = 6/p then 2p = 36
⇒ p = 18
(ii) p/54 = 54/q
⇒ pq = 54 × 54
⇒ 18q = 54 × 54
⇒ q = (54 × 54)/18
= 162
Hence p = 18, q = 162
Question- 10 If a, b, c, d, e are in continued proportion, prove that: a : e = a4 : b4.
Answer -10
a, b, c, d, e are in continued proportion
⇒ a/b = b/c = c/d = d/e = k (say)
d = ek, c = ek2, b = ek3 and a = ek4
Now L.H.S = a/e = (ek4)/e = k4
R.H.S = a4/b4 = (ek4)4/(ek3)4 = (e4k16)/(e4k12)
= k16 – 12
= k4
∴ L.H.S. = R.H.S.
Ratio and Proportion, Ch-Test Questions
ML Aggarwal Class 10 ICSE Maths Solutions Ch-7
Question -11 Find two numbers whose mean proportional is 16 and the third proportional is 128.
Answer- 11
Let x and y be two numbers
Their mean proportion = 16
and third proportion = 128
√xy=16
⇒ xy = 256
⇒ x = 256/y …(i)
And y2/x = 128
⇒ x = y2/128 …(ii)
From (i) and (ii)
256/y = y2/128
⇒ y3 = 256 × 128
= 32768
⇒ y3 = (32)3
⇒ y = 32
∴ x = 256/y = 256/32 = 8
∴ Numbers are 8, 32
Question -12 If q is the mean proportional between p and r, prove that: : p3 – 3q2 + r2 = q4((1/p²-3/q²+1/r²)
Answer -12
q is mean proportional between p and r
q² = pr
L.H.S. = p2 – 3q2 + r2 = p2 – 3pr + r2
R.H.S. = q4(1/p2 – 3/q2 + 1/r2)
= (q2)2 (1/p2 – 3/q2 + 1/r2)
= (pr)2 (1/p2 – 3/q2 + 1/r2)
or (pr)2 (1/p2 – 3/pr + 1/r2)
= p2r2 (r2 – 3pr + p2)/(p2r2)
= r2 – 3pr + p2
∴ L.H.S. = R.H.S
Hence, proved
Question -13 If a/b=c/d=e/f, prove that each ratio is
(i)
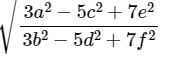
(ii)
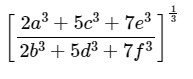
Answer- 13
a/b=c/d=e/f
= k(say)
then a = k, c = dk, e = fk
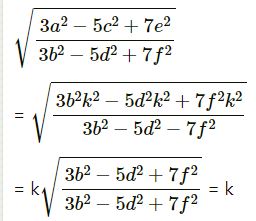
(ii) [(2a3 + 5c3 + 7e3)/(2b3 + 5d3 + 7f3)]1/3
= [(2b3k3 + 5d3k3 + 7f3k3)/(2b3 + 5d3 + 7f3)]1/3
= k[(2b3 + 5d3 + 7f3)/(2b3 + 5d3 + 7f3)] 1/3 = k
Hence, proved.
Question- 14 If x/a=y/b=z/c, prove that (3x³-5y³+4c³) / (3a³-5b³+4c³) = [(3x-5y+4c) / (3a-5b+ac)]³
Answer -14
x/a=y/b=z/c,
= k (say)
x = ak, y = bk, z = ck
L.H.S. = (3x3 – 5y3 + 4z3)/(3a3 – 5b3 + 4c2)
= (3a3k3 – 5b3k3 + 4c3k3)/(3a3 – 5b3 + 4c3)
= k3(3a3 – 5b3 + 4c3)/(3a3 – 5b3 + 4c3) = k3
R.H.S = {(3x – 5y + 4z)/(3a – 5b + 4c)}3
= (3ak – 5bk + 4ck)/(3a – 5b + 4c)3
= {k(3a – 5b + 4c)}/(3a – 5b + 4c)}3
= (k)3
= k3
∴ L.H.S = R.H.S.
Question -15 If x : a = y : b, prove that (x4 + a4) / (x3 + a3) + (y4 + b4) / (y3 + b3) = {(x + y)4 + (a + b)4} / {(x + y)3 + (a + b)3}
Answer -15
x/a = y/b = k (say)
x = ak, y = bk
L.H.S = (x4 + a4)/(x3 + a3) + (y4 + b4)/(y3 + b3)
= (a4k4 + a4)/(a3k3 + a3) + (b4k4 + b4)/(b3k3 + b3)
= {a4(k4 + 1)}/{a3(k3 + 1)} + {b4(k4 + 1)|/{b3(k3 + 1)}
= {a(k4 + 1)/(k3 + 1)} + {b(k4 + 1)/(k3 + 1)}
= {a(k4 + 1) + b(k4 + 1)}/(k3 + 1)
= (k4 + 1)(a + b)/(k3 + 1)
R.H.S = {(x + y)4 + (a + b)4}/{(x + y)3 + (a + b)3}
= {(ak + bk)4 + (a + b)4}/{(ak + bk)3 + (a + b)3}
= {k4(a + b)4 + (a + b)4}/{k3(a + b)3(a + b)3}
= {(a + b)4(k4 + 1)}/{(a + b)3(k3 + 1)}
= {(a + b)(k4 + 1)}/(k3 + 1) = {(k4 + 1)/(a + b)}/(k3 + 1)
∴ L.H.S = R.H.S.
Hence, proved.
Ratio and Proportion, Ch-Test Questions
ML Aggarwal Class 10 ICSE Maths Solutions Ch-7
Question -16 If x/(b + c – a) = y/(c + a – b) = z/(a + b – c) prove that each ratio’s equal to :(x + y + z)/(a + b + c)
Answer -16
x/(b + c – a) = y/(c + a – b) = z/(a + b – c) = k (say)
x = k(b + c – a),
y = k(c + a – b),
z = k(a + b – c),
(x + y + z)/(a + b + c)
= {k(b + c – a) + k(c + a – b) + k(a + b – c)}/(a + b + c)
= {k(b + c – a + c + a – b + a + b – c)}/(a + b + c)
= {k(a + b + c)}/(a +b + c)
= k
Hence, proved.
Question -17 If a : b = 9 : 10, find the value of
(i) (5a+3b)/(5a-3b)
(ii)( 2a²-3b²)/(2a²+3b²)
Answer -17
a : b = 9 : 10
⇒ a/b = 9/10
(i) (5a + 3b)/(5a – 3b)
= (5a/b + 3b/b)/(5a/b – 3b/b)
= (5a/b + 3)/(5a/b – 3)(Dividing by b)
= (5 × 9/10 + 3)/(5 × 9/10 – 3) (Substituting the value of a/b)
= (9/3 + 3)/(9/2 – 3)
= (15/2)/(3/2)
= 15/2 × 2/3
= 5
(ii) (2a2 – 3b2)/(2a2 + 3b2)
= [(2a2/b2 – 3b2/b2]/[2a2/b2 – 3b2/b2] (Dividing by b2)
= {2(a/b)2 – 3}/{2(a/b)2 + 3}
= {2(9/10)2 – 3}/{2(9/10)2 + 3}
= (2 × 81/100 – 3)/(2 × 81/100 + 3)
= (81/50 – 3)/(81/5 + 3)
= {(81 – 150)/50}/{(81 + 150)/50}
= – 69/50 × 50/231
= – 69/231
= – 23/77
Question -18 If (3x² + 2y²) : (3x² – 2y²) = 11 : 9, find the value of ;(3x4 + 5y4)/(3x4 – 5y4)
Answer -18
(3x4 + 2y4)/(3x4 – 2y4) = 11/9
Applying componendo and dividendo,
(3x2 + 2y2 + 3x2 – 2y2)/(3x2 + 2y2 – 3x2 + 2y2)
= (11 + 9)/(11 – 9)
⇒ 6x2/4y2 = 20/2
⇒ 3x2/2y2 = 10
⇒ x2/y2 = 10 × 2/3
= 20/2
(3x4 + 5y4)/(3x4 – 5y4)
= (3x4/y4 + 25y4/y4)/(3x4/y4 – 25y4/y4)
= {3(x2/y2)2 + 25}/{3(x2/y2)2 – 25}
= {3 × (20/3)2 + 25}/{3(20/3)2 – 25}
= (3 × 400/9 + 25)/(3 × 400/9 – 25)
= (400/3 + 25/1)/(400/3 – 25/1)
= {(400 + 75)/3}/{(400 – 75)/3}
= 475/3 × 3/325
= 19/13
Question- 19 If x = 2mab/(a + b), find the value of
{(x + ma)/(x – ma)} + {(x + mb)/(x – mb)}
Answer -19
x = 2mab/(a + b)
⇒ x/ma + 2b/(a + b)
Applying componendo and dividendo
(x + ma)/(x – ma) = (2b + a + b)/(2b – a – b)
= (3b + a)/(b – a) ….(i)
Again x/mb = 2a/(a + b)
Applying componendo and dividendo
(x + mb)/(x – mb)
= (2b + a + b)/(2b – a – b)
= (3b + a)/(a – b) …(ii)
Adding (i) and (ii)
{(x + ma)/(x – ma)} + {(x + mb)/(x – mb)}
= {(3b + a)/(b – a)} + {(3a + b)/(a – b)}
= – {(3b + a)/(a – b)} + {(3a + b)/(a – b)}
or (- 3b – a + 3a + b)/(a – b)
= (2a – 2b)/(a – b)
or {2(a – b)}/(a – b)
= 2
Question -20 If x = pab/(a + b) ,prove that {(x + pa)/(x – pa)} – {(x + pb)/(x – pb)}=2(a2 – b2)/ab
Answer -20
x = pab/(a + b)
⇒ x/pa + b/(a + b)
Applying componendo and dividendo
(x + pa)/(x – pa)
= (b + a + b)/(b – a – b)
= (a + 2b)/-a ….(i)
Again, x/pb = a/(a + b)
Applying componendo and dividendo,
(x + pb)/(x – pb)
= (a + a + b)/(a – a – b)
= {(2a + b)/-b} …(ii)
L.H.S = {(x + pa)/(x – pa)} – {(x + pb)/(x – pb)}
= {(a + 2b)/-a} – {(2a + b)/-b}
= {(a + 2b)/-a} + {(2a + b)/b}
= {(ab + 2b2 – 2a2 – ab)/(-ab)}
= {(2b2 – 2a2)/(-ab)}
= (- 2a2 + 2b2)/(- ab)
= {-2(a2 – b2)/(-ab)}
= 2(a2 – b2)/ab
= R.H.S.
Ratio and Proportion, Ch-Test Questions
ML Aggarwal Class 10 ICSE Maths Solutions Ch-7
Question- 21 Find x from the equation (a+x+√a²x²) / (a+x-√a²-x²) = b/x
Answer -21
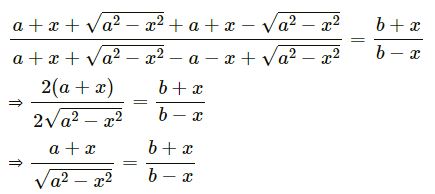
Squaring both sides,
{(a + x)2}/(a2 – x2) = {(b + x)2}/{(b – x)2}
⇒ {(a + x)2}/{(a + x)(a – x)} = {(b + x)2/(b – x)2}
⇒ (a + x)/(a – x) = (b + x)2/(b – x)2
Again applying componendo and dividendo,
(a + x + a – x)/(a + x – a + x) = (b + x)2 + (b – x)2 /(b + x)2 – (b – x)2
⇒ 2a/2x = {2(b2 + x2)/4bx}
⇒ a/x = (b2 + x2)/2bx
2bx = x(b2 + x2)
⇒ 2ab = b2 + x2
⇒ x2 = 2ab – b2
Question -22

Answer- 22
Applying componendo and dividendo,
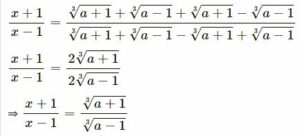
Cubing both sides
(x + 1)3/(x – 1)3 = (a + 1)/(a – 1)
Again applying componendo and dividendo,
{(x + 1)3 + (x – 1)3}/{(x + 1)3 – (x – 1)3}
= (a + 1 + a – 1)/(a + 1 – a + 1)
⇒ {2(x3 + 3x)}/{2(3x2 + 1)} = 2a/2
⇒ (x3 + 3x)/(3x2 + 1) = a/1
⇒ x3 + 3x = 3ax2 + a
⇒ x3 – 3ax2 + 3x – a = 0
Hence, proved.
— : End of ML Aggarwal Ratio and Proportion Ch-Test Questions for ICSE Class 10 Maths Solutions Ch-7 :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


