Newton Law of Motion Obj-2 HC Verma Solutions Concept of Physics Vol-1 Ch-5 for Class-11. Step by Step Solution of Objective -2 (MCQ-2) Questions of Ch-5 Newton Law of Motion (Concept of Physics) with Figure and explanation .Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Newton Law of Motion Obj-2 (MCQ-2) HC Verma Solutions Concept of Physics Vol-1 Ch-5 for Class-11
| Board | ISC and other board |
| Publications | Bharti Bhawan Publishers |
| Ch-5 | Newton Law of Motion |
| Class | 11 |
| Vol | 1st |
| writer | H C Verma |
| Book Name | Concept of Physics |
| Topics | Solution of Objective-2 (MCQ-2) Questions |
| Page-Number | 78, 79 |
-: Select Topics :-
Objective-II (Currently Open)
Exercise (update Soon)
Newton Law of Motion Obj-2 (MCQ-2)
HC Verma Solutions Concept of Physics Vol-1 Ch-5 for Class-11
Page-78
Question-1
A reference frame attached to the earth
(a) is an inertial frame by definition
(b) cannot be an inertial frame because the earth is revolving around the sun
(c) is an inertial frame because Newton’s laws are applicable in this frame
(d) cannot be an inertial frame because the earth is rotating about its axis.
Answer-1
The options, (b) and (d) are correct
Explanation:
A reference frame attached to the earth cannot be an inertial frame because the earth is revolving around the sun and also rotating about its axis.
Question-2
A particle stays at rest as seen in a frame. We can conclude that
(a) the frame is inertial
(b) resultant force on the particle is zero
(c) the frame may be inertial but the resultant force on the particle is zero
(d) the frame may be non-inertial but there is a non-zero resultant force
Answer-2
The options, (c) and (d) are correct
Explanation:
According to Newton’s second law which says that net force acting on the particle is equal to rate of change of momentum ( or mathematically F = ma), so if a particle is at rest then
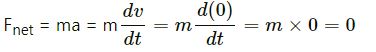
Now, if the frame is inertial, then the resultant force on the particle is zero.
If the frame is non-inertial,
vector sum of all the forces plus a pseudo force is zero.
i.e. Fnet ≠ 0.
Question-3
A particle is found to be at rest when seen from a frame S1 and moving with constant velocity when seen from another frame S2. Mark out the possible options.
(a) Both the frames are inertial.
(b) Both the frames are non-inertial.
(c) S1 is inertial and S2 is non-inertial.
(d) S1 is non-inertial and S2 is inertial
Answer-3
The options, (a) and (b) are correct
Explanation:
S1 is moving with constant velocity w.r.t frame S2. So, if S1 is inertial, then S2 will be inertial and if S1 is non-inertial, then S2 will be non-inertial.
Question-4
The figure (5-Q.3) shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
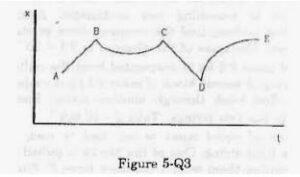
(a) AB
(b) BC
(c) CD
(d) DE
Answer-4
The options, (a) and (c) are correct
Explanation:
Slope of the x-t graph gives velocity. In the regions AB and CD, slope or velocity is constant, i.e. acceleration is zero. Hence, from the second law, force is zero in these regions.
Question-5
The figure (5-Q.4) shows a heavy block kept on a frictionless surface and being pulled by two ropes of equal mass m. At t = 0, the force on the left rope is withdrawn but the force on the right end continues to act. Let F1 and F2 be the magnitudes of the forces exerted by right rope and the left rope on the block, respectively.
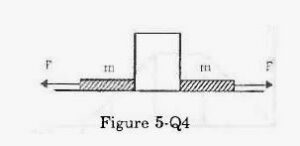
(a) F1 = F2 = F for t < 0
(b)F1 = F2 = F + mg for t < 0
(c) F1 = F, F2 = F for t > 0
(d) F1 < F, F2 = F for t > 0
Answer-5
The option, (a) is correct
Explanation:
At t < 0, the block is in equilibrium in the horizontal direction.
So, F1 = F2 = F
At t > 0, F2 = 0 and F1 = F.
Page-79
Question-6
The force exerted by the floor of an elevator on the foot of a person is more than the weight of the person if the elevator is
(a) going up and slowing down
(b) going up and speeding up
(c) going down and slowing down
(d) going down and speeding up
Answer-6
The options, (b) and (c) are correct
Explanation:
It means normal force exerted by the floor of the elevator on the person is greater that the weight of the person.
i.e. N > mg
(i) Going up and speeding up:
aeff = g + a
N = maeff = mg + ma (N > mg)
(ii) Going down and speeding up:
aeff = g – a
N = mg – ma (N < mg)
(iii) Going down and slowing down:
aeff = g – (–a) = g + a
N = mg + ma (N > mg)
(iv) Going up and slowing down:
aeff = g – a
N = mg – ma (N < mg)
Question-7
If the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be
(a) going up with increasing speed
(b) going down with increasing speed
(c) going up with uniform speed
(d) going down with uniform speed
Answer-7
The options, (c) and (d) are correct
Explanation:
Tension in the cable = Weight of the elevator
Or, total upward force = total downward force
That is, there’s no acceleration or uniform velocity.
So, the elevator is going up/down with uniform speed.
Question-8
A particle is observed from two frames S1 and S2. Frame S2 moves with respect to S1with an acceleration a. Let F1 and F2 be the pseudo forces on the particle when seen from S1 and S2, respectively. Which of the following is not possible?
(a) F1 = 0, F2 ≠ 0
(b) F1 ≠ 0, F2 = 0
(c) F1 ≠ 0, F2 ≠ 0
(d) F1 = 0, F2 = 0
Answer-8
The option, (d) is correct
Explanation:
![]()
Acceleration of the particle w.r.t. to S1 = F1/m
Acceleration of the particle w.r.t. to S2 = F2/m
If we assume F1 = 0 and F2 = 0,
hence, we can conclude that
![]()
From equations (1) and (2), we can say that our assumption is wrong.
And F1 = 0, F2 = 0 is not possible
Question-9
A person says that he measured the acceleration of a particle to be non-zero even though no force was acting on the particle.
(a) He is a liar.
(b) His clock might have run slow.
(c) His metre scale might have been longer than the standard.
(d) He might have used a non-inertial frame.
Answer-9
The option, (d) is correct
Explanation:
If no force is acting on a particle and yet, its acceleration is non-zero, it means the observer is in a non-inertial frame.
—: End of Newton Law of Motion Obj-2 (MCQ-2) HC Verma Solutions Vol-I Concept of Physics:–
Thanks


