OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8. Step by step Solutions of OP Malhotra SK Gupta, Anubhuti Gangal S.Chand ISC Class-12 Mathematics with Exe-8(a), Exe-8(b), Exe-8(c), Exe-8(d), Exe-8(e), Exe-8(f), Exe-8(g), Exe-8(h), Exe-8(i), Exe-8(j), Exe-8(k), Exe-8(l), Self Revision and Chapter Test Questions. Visit official Website CISCE for detail information about ISC Board Class-12 Mathematics.

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Class:	12th
Subject:	Mathematics
Chapter  :	Ch-8 Differentiation of Section -A

Board	ISC
Writer	OP Malhotra, SK Gupta, Anubhuti Gangal
Publications	S.Chand Publications 2020-21

---

-: Included Topics :- 

Exe-8(a)

Exe-8(b)

Exe-8(c)

Exe-8(d)

Exe-8(e)

Exe-8(f)

Exe-8(g)

Exe-8(h)

Exe-8(i)

Exe-8(j)

Exe-8(k)

Exe-8(l)

Self Revision

Chapter Test

---

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Differentiation :  The process of finding a derivative of a function is called differentiation.

Differentiation in Maths :

In Mathematics, Differentiation can be defined as a derivative of a function with respect to an independent variable. Differentiation, in calculus, can be applied to measure the function per unit change in the independent variable.

Let y = f(x) be a function of x. Then, the rate of change of “y” per unit change in “x” is given by:

dy / dx

If the function f(x) undergoes an infinitesimal change of ‘h’ near to any point ‘x’, then the derivative of the function is defined as :

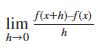
Derivative of Function As Limits :

If we are given with real valued function (f) and x is a point in its domain of definition, then the derivative of function, f, is given by:

f'(a) = lim_h→0[f(x+h)-f(x)]/h

provided this limit exists.

Let us see an example here for better understanding.

Example:

Find the derivative of f=2x, at x =3 :

Solution: By using the above formulas, we can find,

f'(3) = lim_h→0[f(3+h)-f(3]/h = lim_h→0[2(3+h)-2(3)]/h

f'(3) = lim_h→0[6+2h-6]/h

f'(3) = lim_h→02h/h

f'(3) = lim_h→02 = 2

---

Exe-8(a)

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Differentiate with respect to x :

Question 1:

(i) x⁵

(ii) 6x⁸

(iii) …………..

………………

Question 2:

………………………

………………………

……………………..

Question 11:

Differential from  first principle .

(i) 3x

(ii) (x + 1) (2x – 3)

(iii)……….

………………..

---

Exe-8(b)

 Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Question 1:

(i) (5x + 7)5

(ii) …………..

………………….

Question 2:

……………………….

………………………..

…………………………

Question 30:

Given y = (3x – 1)² + (2x – 1)³, …………….. dy/dx = 0.

---

Exe-8(c)

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Differentiate the following function w.r.t. x:

Question 1:

sin²(x²)

Question 2:

………………………

…………………….

………………………

Question 15:

If y = 2  tan x/2, prove that dy/dx = 2/(1 + cosx)

---

Exe-8(d)

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Differentiate  w.r.t. x:

Question 1:

(i) log cos x

(ii) log sin x

(iii)………..

……………..

Question 2:

…………………..

…………………..

…………………….

Question 24:

If y = ………………

---

Exe-8(e)

 Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Differentiate  w.r.t. x:

Question 1:

(i) e^3x

(ii) e^{cos x}

(iii) ……………

…………………

Question 2:

…………………….

………………………

………………………

Question 10:

e^x.log (1 + x²)

---

Differentiation Formulas :

The important Differentiation formulas are given below in the table. Here, let us consider f(x) is a function and f'(x) is the derivative of the function.

1.     If f(x) = tan (x), then f'(x) = sec2x 2.     If f(x) = cos (x), then f'(x) = -sin x 3.     If f(x) = sin (x), then f'(x) = cos x 4.     If f(x) = ln(x), then f'(x) = 1/x 5.     If f(x) = ex then f'(x) = exex 6.     If f(x) = xn xn where n is any fraction or integer, then f'(x) = nxn-1 7.     If f(x) = k, where k is a constant, then f'(x) = 0

Differentiation Rules :

The basic differentiation rules that need to be followed are as follows:

• Sum and Difference Rule
• Quotient Rule
• Chain Rule
• Product Rule

Let us discuss here.

Sum or Difference Rule :

If the function is sum or difference of two functions, the derivative of the functions is the sum or difference of the individual functions, i.e.,

If f(x) = u(x) ± v(x)

then, f'(x)=u'(x) ± v'(x)

Quotient rule :

If the function f(x) is in the form of two functions [u(x)]/[v(x)], the derivative of the function is

Chain Rule :

If a function y = f(x) = g(u) and if u = h(x), then the chain rule for differentiation is defined as,

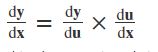
This plays a major role in the method of substitution that helps to perform differentiation of composite functions.

Product Rule :

As per the product rule, if the function f(x) is product of two functions u(x) and v(x), the derivative of the function is,

---

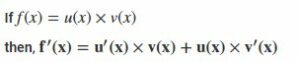
Exe-8(f)

 Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Differentiate  w.r.t. x the following function

Question 1:

sin-1(3x)

Question 2:

……………………..

……………………..

………………………

Question 14:

x√a²……………….

---

Exe-8(g)

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Differentiate the following w.r.t. x :

Question 1:

(i) cos -1 (cos x)

(ii) tan -1 (cot x)

Question 2:

…………………….

……………………..

………………………

Question 27:

sin²[cot-1…………….]

---

Exe-8(h)

 Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Find dy/dx if

Question 1:

x² + y² = a²

Question 2:

…………………….

…………………….

……………………..

Question 20:

If y = √cos x + …………..

---

Exe-8(i)

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Find dy/dx

Question 1:

if x = ct, y = c/t

Question 2:

…………………….

…………………….

………………………

Question 10:

If x = a (cos θ + log tan θ/2)

---

Exe-8(j)

 Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Differentiate :

Question 1:

x² w.r.t. x³

Question 2:

…………………..

……………………..

…………………..

Question 5:

Differentiate

(i) tan -1…………

(ii) tan -1 x/………….

…………………….

---

Exe-8(k)

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Find the derivative of the following function :

Question 1:

(x² + 2)³ (1 – x³)⁴

Question 2:

…………………..

……………………

…………………….

Question 27:

Differentiate (sin x)^x wrt x²

---

Real-Life Applications of Differentiation :

With the help of differentiation, we are able to find the rate of change of one quantity with respect to another. Some of the examples are:

• Acceleration: Rate of change of velocity with respect to time
• To find tangent and normal to a curve
• To calculate the highest and lowest point of the curve in a graph or to know its turning point, the derivative function is used

---

Exe-8(l)

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Find the second derivative of the following function :

Question 1:

(i) x²

(ii) a^x

(iii)………….

……………..

Question 2:

…………………

……………..

…………………

Question 20:

If x = cos θ, y =  sin³ θ ………………………….. .

---

Self Revision

Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Question 1:

If y = log ……….. find dy/dx.

Question 2:

……………………

……………………..

……………………..

Question 23:

If log y = tan -1x, prove that ……………….

---

Chapter Test

OP Malhotra Differentiation S.Chand ISC Class-12 Maths Solutions Ch-8

Find dy/dx If

Question 1:

y = sin x log x

Question 2:

…………………….

…………………….

………………………

Question 25:

If y = e^x(sin x + cos x), then show that ……………………… = 0.

-: End of Differentiation OP Malhotra S. Chand ISC Class-12 Maths Chapter-8 Solution :-

Return to :-  OP Malhotra S. Chand ISC Class-12 Maths Solutions

---

Thanks

Please share with your friends