Polygon Class-6 RS Aggarwal ICSE Maths Goyal Brothers Prakashan Solutions Chapter-19 Solutions. We provide step by step Solutions of Exercise / lesson-19 Polygon for ICSE Class-6 RS Aggarwal Mathematics.
Our Solutions contain all type Questions with Exe-19 with Notes on Polygon to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6 Maths.
| Board | ICSE |
| Publications | Goyal brothers Prakshan |
| Subject | Maths |
| Class | 6th |
| Chapter-19 | Polygon |
| Writer | RS Aggrawal |
| Book Name | Foundation |
| Topics | Solution of Exe-19 |
| Academic Session | 2021-2022 |
Polygon Class-6 RS Aggarwal ICSE Maths Goyal Brothers Prakashan Solutions Chapter-19 Solutions
–: Select Topics :–
Notes on Polygon
A polygon is a closed figure bounded by three or more line segments that intersect exactly to form a closed curve.
Basic Terms in Polygons
- Sides: The line segments that forms a polygon is termed as sides. From the above polygon, we can say that line segment AB, BC, CD, DA are four sides of the polygon.
- Vertex: The meeting of two sides is termed as vertex. From the above polygon, we can say that A is a vertex as DA and AB meets at A. Similarly, B, C and D are also vertices of the polygon.
- Adjacent Sides: In a polygon, any two sides that has a common end are termed as adjacent sides. From the above polygon, we can say that sides CD and BC are adjacent as they terminate at a common end C. Similarly, sides AB and DA, AB and BC, CD and DA are also adjacent.
- Adjacent Vertices: End points of the same side of the polygon are termed as adjacent vertex. From the above polygon, we can say that C and D are adjacent vertices while A and C are not adjacent vertices.
- Diagonals: The line joining the non-adjacent vertices of a polygon is termed as diagonals. From the above polygon, we can say that line segment AC and DB are the diagonals of the polygon.
classification of polygons
Regular Polygon
In a regular polygon, all the sides of the polygon are equal, and all the interior angles are the same.
Irregular Polygon
A polygon with an irregular shape. It means the sides and angles of the polygon are not equal.
Convex Polygon
In a convex polygon, the measure of the interior angle is less than 180 degrees
Concave Polygon
In a concave polygon, at least one angle measures more than 180 degrees. The vertices of a concave polygon are inwards as well as outwards
| Name of the Polygons | Sides | Vertices | Angle |
| Triangle (also called Trigon) | 3 | 3 | 60° |
| Quadrilateral (also called Tetragon) | 4 | 4 | 90° |
| Pentagon | 5 | 5 | 108° |
| Hexagon | 6 | 6 | 120° |
Important for Polygon
Exterior angle + Adjacent Angle = 180°
Sum of the All interior angles of n side polygon = (2n-4) x 90
Exe-19
Polygon Class-6 RS Aggarwal ICSE Maths Goyal Brothers Prakashan Solutions Chapter-19 Solutions
Page 233-234
Question 1:
Which of the following are simple closed figures ?

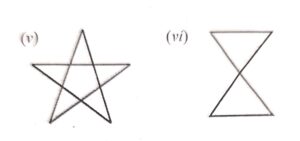
Answer :
Figures (i), (ii) and (iv) are simple closed figures.
Question 2:
Which of the following figures are polygons ? Name them, if any.
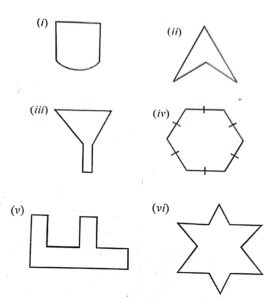
Answer :
(i) No.
(ii) Yes, this is concave quadrilateral.
(iii) Yes, concave hexagon.
(iv) Yes, regular hexagon.
(v) Yes, concave decagon.
(vi) Yes, concave 12-gon.
Question 3:
Find the sum of the interior angles of a :
(i) nonagon
(ii) 16-sided polygon
Answer :
(i) A nonagon has 9 sides
so, sum of interior angles of nonagon
= (2 x 9 – 4) right angle
= 14 x 90° = 1260°
(ii) Sum of interior angles of a 16 sided polygon
= (2 x 16 – 4) right angle.
= 28 x 90° = 2520°
Question 4:
Find the measure of each interior angle of a :
(i) regular decagon
(ii) regular 18-sided polygon
Answer :
(i) A decagon has 10 sides
Sum of interior angles of a decagon
= (2 x 10 – 4) right angles
16 x 90° = 1440°
Since, the interior angles of a regular polygon are of the same measures,
so we have each interior angle of (1440°/10)
= 144° regular decagon
(ii) Sum of interior angle of a regular 18-sided polygon
= (2 x 18 – 4) x 90° = 2880°
Since, the interior angles of a regular polygon are of the same measure,
so we have each interior angle of (2880/18) = 160° g
Question 5:
Five of the angles of a hexagon are each 115°. Calculate the measure of the sixth angle.
Answer :
A hexagon has 6 sides
Sum of interior angles of a hexagon
= (2 x 6 – 4) right angles
= 8 x 90°
= 720°
Sixth angle= 720° – (115° + 115° + 115 + 115° + 115°)
= 720° – 575°
= 145°
Question 6:
The angles of a heptagon are (x + 3)°, (2x + 5)°. Cr+8)°, (3x + 1)°, (5x – 6)°, (2x + 9)° and (x -5)°. Calculate x.
Answer :
In a heptagon, n =7
So, Sum of its interior angles
= (2 – 4) right angles
= (2 x 7 – 4) x 90°
(14 – 4) x 90°
10 x 90° = 900°
But sum of its angles are :
(x + 3)° + (2x + 5)° + (x + 8)° + (3x + 1)° + (5x – 6)° + (2x + 9)° + (x – 5)°
= X + 3 + 2x + 5 + X + 8 + 3x + 1 + 5x -6 + 2x + 9 + x – 5
= 15x + 26 – 11 = 15 x+ 15°
= 15x = 900° – 15° 885°
= x = (885°/15°) = 59°
Hence,
x = 59°
Question 7:
An octagon has three equal angles each of measure 11S°. If all the remaining angles have equal measure, find the measure of each of these remaining angle.
Answer :
Sum of angles of an octagon (n = 8)
= (2n – 4) angles
=(2 x 8 – 4) x 90° = (16-4) x 90°
12 x 90° = 1080°
Sum of three angles of it = 115° x 3 = 345°
So, Sum of remaining 5 angles 1080° – 345° = 735°
So, Measure of each angle = (735°/5) = 147°
Question 8:
The sum of the interior angles of a polygon is 2160°. How many sides does this polygon have ?
Answer :
The number of sides of the polygon be n.
Then, sum of interior angles of the polygon
= (2n – 4) right angles
= (2n – 4) x 90°
So, (2n – 4) x 90° = 2160°
= (2n – 4) = 2160/90
= 24
= 2n = 28
= n = 14
Find the number o sid6s of a polygon if each of its interior angles measure :
(i) 140°
(ii) 162°
(iii) 150°
Answer :
(i)
Then, sum of its interior angles
Measure of each interior angle[(2n-4)x90°/n]
So, [(2n-4) x 90°/n] = 140
= (2n – 4) x 90° = 140 n
= 180n – 360° = 140 n
= 180n – 140 = 360
= 40n = 360°
n = (360°/40) = 9
Hence, the polygon has 9 sides.
(ii)
Let the number of sides of the polygon be n.
Then, sum of its interior angles
Measure of each interior angle= [(2n – 4) x 90°/n]
= [(2n-4) x 90°/n] = 162°
= (2n-4) x 90° = 162 n
= 180n – 360° = 162 n
= 180n – 162 n= 360
= 18n = 360
n = (360/18) = 20
Hence, the polygon has 20 sides.
(iii)
Let the number of sides of the polygon be n.
Then, sum of its interior angles = (2n-4) right angles
Measure of each interior angle
= [(2n – 4) x 90°/n]
= [(2n-4) x 90°/n] = 150°
= (2n-4) x 90° = 150 n
= 180n – 360° = 150 n
= 180n – 150 n= 360
= 30n = 360
n = (360/30) = 12
Hence, the polygon has 12 sides.
Question 10:
Find the measure of each exterior angle of a regular decagon.
Answer :
Each interior angle = [(2 x 10 – 4) x 90°/10]
= 144°
Each exterior angle = 180° – Each interior angle = 180° – 144°
= 36°
So, Each exterior angle of a regular decagon = 36°
–: End of Polygon Class-6 RS Aggarwal Solutions :–
Return to- RS Aggarwal Solutions for ICSE Class-6 Goyal Brothers Prakashan
Thanks



Very nice
thanks