Problems on Quadratic Equations RS Aggarwal ICSE Class 10 Chapter-6. RS Aggarwal Solutions of Problems on Quadratic Equations Chapter 6 for ICSE Maths Class-10 is also called Goyal Brother Prakashan . This post is The Solutions of word Problems on Quadratic for Chapter – 6 Problems on Quadratic Equations of RS Aggarwal which is common famous Maths writer in ICSE Board in Maths Publication as Goyal Brothers Prakashan.
Problems on Quadratic Equations RS Aggarwal ICSE Class 10 Goyal Brothers
Step by Step Solutions of Chapter-6 Problems on Quadratic Equations is given to understand the topic clearly of RS Aggarwal Goyal Brothers Prakashan. Chapter Wise Solution of RS Aggarwal including Chapter -6 Problem on Quadratic Equation is very help full for ICSE Class 10th student appearing in 2020 exam of council.Students appearing in ICSE class 10th exam can check ICSE class 10th exam pattern 2020 on its official website www.cisce.org.
Problems on Quadratic Equations RS Aggarwal Chapter-6 for ICSE Class-10
Note:- Before viewing Solutions of Chapter-6 Problems on Quadratic Equations of RS Aggarwal Goyal Brother Prakashan Solutions. Read the Chapter Carefully . Then solve all example of your text book with formula and concept of ICSE Class 10 Maths .The Chapter 6 Problem on Quadratic Equation is main Chapter in ICSE board Class 10.Practice Previous Year Solved Question Paper ICSE Boardto enhance the confidence in more effective way.
What is Quadratic Equation
A quadratic equation is an equation that can be written in the standard form ax2+bx+c=0 , where a≠0 and a, b, and c are integers.
The quadratic equations are very useful in real world situations
Many word problems Involving unknown quantities can be translated for solving quadratic equations
how to frame/create the equations from word problem:
Methods of solving quadratic equations are discussed here in the following steps.
1st Step : Denote the unknown quantities by x, y etc.
2nd Step : use the conditions of the problem to establish in unknown quantities.
3rd Step : Use the equations to establish one quadratic equation in one unknown.
4th Step : Solve this equation to obtain the value of the unknown in the set to which it belongs.
EXERCISE – 6 Problems on Quadratic Equations RS Aggarwal
Page 63
Question 1
Find two natural numbers whose sum is 50 and product 525.
Answer :
let the required number be x and y
so according to the question
x+ y = 50 ——-(1)
xy = 525 ——-(2)
so put y = 525/x in eqn (1)
=> x + 525/x = 50
=> x² + 525 = 50x
=> x² – 50x +525 = 0
=> x² -35x – 15x + 525 =0
=> x(x – 35) -15(x – 35) =0
=> (x – 35)(x – 15) = 0
=> x – 35 = 0
or x – 15 = 0
=> x = 35 , 15
Question 2
The difference between two natural numbers is 4 and their product is 221. Find the numbers.
Answer :
let the two numbers be X and Y
A/Q-
X – Y = 4
and
XY = 221
Y(4+Y)= 221
Y² + 4Y -221= 0
Y² +17Y – 13Y – 221 = 0
Y(Y + 17) – 13(Y + 17)=0
(Y – 13)(Y + 17)=0
Y – 13 = 0 or
Y + 17= 0
Since Y is natural number so , Y = 13
then X= 17
Question 3
Find two consecutive positive even integers whose product is 224.
Answer :

Question 4
Find two consecutive natural numbers, the sum of whose squares is 145.
Answer :
Let one number be x
Then other number = x+1
It i s given that the sum of square of those numbers is 145.
Therefore,
x² + (x+1)² = 145.
x² + x² + 2x + 1 = 145 {(a+b)²= a² + 2ab + b²}
2x² + 2x – 144 = 0
Dividing both sides by 2, we obtain
x² + x – 72 = 0
x² – 8x + 9x – 72 = 0
x(x-8) + 9 (x-8) = 0
(x+9) (x-8) = 0
x = -9 or x=8
As x = -9 can’t be answer because it is not a natural number.
Hence, x = 8.
And, x+1 = 9.
Question 5
The sum of two natural numbers is 12 and the sum of their squares is 74. Find the numbers.
Answer :
x+y = 12 [eq. 1]
x² + y² = 74
ATQ
(x + y)² = x² + 2xy + y²
12² = 74 + 2xy
144 = 74 + 2xy
70 = 2xy
xy = 35.
NOW (x+y)² – 4xy = (x – y)²
so 144 – 140 = 4
so x-y = 2 [eq. 2]
solving 1 &2
x + y + x – y = 2 + 12
2x = 14
x = 7
and y = 5
Question 6
Find two consecutive multiples of 3 whose product is 270.
Answer :
Let the two consecutive multiples of 3 are 3x and 3x + 3
Given that their product is 270
⇒ (3x) (3x + 3) = 270
⇒ x(3x + 3) = 90
⇒ 𝑥2 + 𝑥 – 30 = 0
⇒ 𝑥2 + 6𝑥 – 5𝑥 – 30 = 0
⇒ x(x + 6) – 5(x + 6) = 0
⇒ (x + 6) (x – 5) = 0
⇒ x = 5 or x = -6
Considering the positive value of x.
⇒ x = 5, 3x = 15 and 3x + 3 = 18
∴ The two consecutive multiples of 3 are 15 and 18.
Question 7
The sum of a natural number and its reciprocal is 65/8. Find the natural number.
Answer :
Let the natural number be x.
According to the given condition,
x + 1/x = 658
⇒ (x² + 1)/x = 65/8
⇒8x² + 8=65x
⇒8x² – 65x+8=0
⇒8x² – 64x-x+8=0
⇒8x (x – 8) – 1(x – 8) = 0
⇒(x – 8)( 8x – 1)=0
⇒or x – 8 = 0 or 8x- 1=0
⇒or x= 8 or x = 1/8
∴x = 8 (x is a natural number)
Question 8
Divide 27 into two parts such that the sum of their reciprocals 3/20.
Answer :
et the two parts be x and (27 – x)
1/x + 1/(27 – x) = 3/20
⇒ (27 – x + x )/x(27 – x) = 3/20
⇒ 27/(27x-x²) = 3/20
⇒ 27x – x² = 180
⇒ x² – 27x + 180=0
⇒ x²-15x-12x +180=0
⇒ x(x – 15) – 12(x – 15)=0
⇒ (x – 12)(x – 15) = 0
⇒or x – 12 = 0 or x – 15 = 0
⇒ or x = 12 or x – 15
When x = 12,
27 – x = 27 – 12 = 15
When x = 15
27 – x = 27 – 15 = 15
Hence, the required parts are 12 and 15.
Question 9
The sum of the squares of three consecutive odd numbers is 2531. Find the numbers.
Answer :
Let the numbers be x, x + 2 and x + 4.
⇒ x² + (x + 2)² + (x + 4)² = 2531
⇒ 3x² + 12x – 2511 = 0
⇒ x² + 4x – 837 = 0
⇒ (x – 27) (x + 31) = 0
⇒ x = 27.
Hence,
the required numbers are 27, 29 and 31.
Question 10
The product of two consecutive natural numbers which are multiples of 3 is equal to 810. Find the two numbers.
Answer :
Let the numbers be 3x, 3 (x +1)
According to question, (3x) × 3( x + 1) = 810
9[x² + x] = 810
x² + x = 90
x² + x- 90 = 0
x² + 10x – 9x – 90 = 0
x ( x + 10) – 9 ( x +10 ) = 0
(x – 9) (x + 10 ) = 0
x = 9 , x = – 10
But x ≠ – 10, because 3x must be natural number .
∴ x = 9
Numbers are 3x, 3 (x +1 )
⇒ 3 × 9 , 3(9 + 1)
∴ Numbers are ⇒ 27 , 30
Question 11
A number consists of two digits whose product is 18. If 27 is added to the number, the digits interchange their places. Find the number.
Answer :
et the number be x y where X is tens digit and y is unit digit then
X * y = 18
X = 18/y
now
10x + y + 27 = 10y + X
9x – 9y +27 = 0
X -y +3 = 0
(18/y) -y +3 = 0
18 – y² + 3y = 0
y² – 3y -18 = 0
y² -6y + 3y -18 = 0
y ( y – 6) + 3(y – 6) = 0
( y – 6) ( y + 3) = 0
y = 6 or -3 ( neglecting -3)
y = 6
X = 3
so the number is 36
Question 12
A two-digit number contains the smaller of the two digits in the unit place. The product of the digit is 40 and the difference between the digits is 3. Find the number.
Answer :

Question 13
The sum of the numerator and denominator of a certain fraction is 10. If 1 is subtracted from both the numerator and denominator, the fraction is decreased by 2/21. Find the fraction.
Answer :
et x be the numerator of the fraction
⇒ denominator = 10-x
According to the question,
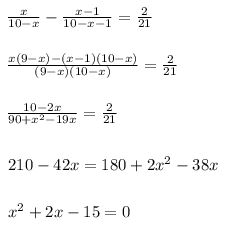
on solving this quadratic equation we get,
x = -5 and 3
faction does not have negative numerator
Numerator, x = 3 and denominator = 10 – x = 7
Therefore, The fraction is 3/7
Question 14
Two years ago, a man’s age was three times the square of his son’ age. In three years time, his age will be four times his son’s age. Find their present ages.
Answer :
Let the age of son 2 years ago be x years.
Then, father’s age 2 years ago = 3x2 years
Present age of son = (x + 2) years
Present age of father = (3x2 + 2) years
3 years hence:
Son’s age = (x + 2 + 3) years = (x + 5) years
Father’s age = (3x2 + 2 + 3) years = (3x2 + 5) years
3x2 + 5 = 4(x + 5)
3x2 – 4x – 15 = 0
3x2 – 9x + 5x – 15 = 0
3x(x – 3) + 5(x – 3) = 0
(x – 3) (3x + 5) = 0
x = 3,
Since, age cannot be negative. So, x = 3.
Present age of son = (x + 2) years = 5 years
Present age of father = (3x2 + 2) years = 29 years
Question 15
Ashish goes to his friends house which is 12 km away from his house. He covers half of the distance at a speed of x km per hour and the remaining at (x + 2) km per hour. If he takes 2 hrs 30 min. to cover the whole distance, find the value of x.
Answer :
Time = Distance/Speed
Given the Ashish covers a distance of 6 km at a speed x km/hr
Time taken to cover first 6 km = 6/x
Also the Ashish covers the remaining 6 km distance at a speed (x + 2) km/hr.
Time taken to cover next 6 km = 6/(x+2)
Time taken to cover the whole distance = 2 hrs 30 mins – 2
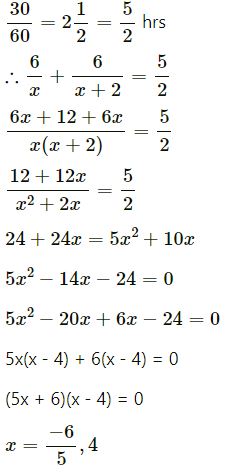
Since speed cannot be negative. Therefore x = 4
Question 16
By increasing the speed of a car by 10 km/hr, the time of journey of 72 km 15 reduced by 36 minutes. Find the original speed of the car.
Answer :
Let original speed be x km/hr.
∴ Time = 72/x hr.
New speed = x + 10 km/hr.
∴ New time = 72/(x+10) hr.
Difference in time = 36 mins.
∴ (72/x ) – 72/(x+10) = 36/60
(72x + 720 – 72x)/x(x+10)=35
5 x 720 = 3 (x2 + 10x)
1,200 = x2 + 10x
x2 + 10x – 1,200 = 0
x2 + 40x – 30x – 1,200 = 0
x (x + 40) – 30 (x + 40) = 0
(x – 30) (x + 40) = 0
∴ x = 30
as x = -40 is not acceptable
∴ Original speed = 30km/hr.
Question 17
A train covers a distance of 600 km at x km/hr. Had the speed been (x + 20) km/hr, the time taken to cover the same distance would have been reduced by 1 hours. Write down an equation in x and solve it to evaluate x.
Answer :
according to the question
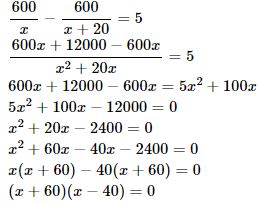
Question 18
A train covers a distance of 780 km at x km/hr. Had the speed been (x – 5) km/hr, the time taken to cover the same distance would have been increased by 1 hour. Write down an equation in x and solve it to evaluate x.
Answer :
distance covered=780km/h
T1=780/x
T2=780/(x-5)
T2-T1=1
[780/(x – 5)]-[780/x]=1
780[(1/x – 5)-(1/x)]=1
780[(x – x + 5)/(x² – 5x)]=1
780 × 5=x² – 5x
3900 = x² – 5x
x² – 5x – 3900 = 0
x² – 65x + 60 x – 3900=0
x(x – 65) + 60(x – 65)=0
(x + 60)(x – 65)=0
x + 60 = 0
x = -60[rejected]
x – 65 = 0
x = 65 km/h
Question 19
The distance by road between two towns A and B, is 216 km, and by rail it is 208 km. A car travels at a speed of x km/hr and the train travels at a speed which is 16 km/hr faster than the car.
(i) Write down the time taken by the car to reach town B from A, in terms of x.
(ii) Write down the time taken by the train to reach town B from A, in terms of x.
(iii) If the train takes 2 hours less than the car to reach town B, obtain an equation in x and solve it.
(iv) Hence, find the speed of the train.
Answer :
Speed of car = x km/hr
Speed of train = (x + 16) km/hr
1) we know Time = Distance/Speed
Time is taken by the car to reach town B From A = 216/x hrs
2) Time taken by the train to reach town B from A = 208/(x+16) hrs
3) From the given information

(x + 48)(x – 36) = 0
x = -48, 36
But speed cannnot be negative So x = 36
4) Speed of train = (36 + 16) km/ hr = 52 km/hr
Question 20
Car A travels x km for every litre of petrol, while car B travels ( x + 5) km for every litre of petrol.
(i) Write down the number of litres used by car A and car B in covering a distance of 400 km.
(ii) If car A used 4 litres of petrol more than car B in covering 400 km, write an equation in x and solve it to determine the number of litres of petrol used by car B for the journey.
Answer :
Distance travelled by car A in one litre = x km
and distance travelled by car B in one litre = (x + 5) km
(i) Consumption of car A in covering 400 km
= 400/x litres and consumption of car B
= 400/(x+5) litres
(ii) According to the conditions,
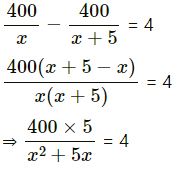
⇒ 2000 = 4x2 + 20x
⇒ 4x2 + 20x – 2000 = 0
⇒ x2 + 5x – 500 = 0 …(Dividing by 2)
⇒ x2 + 25x – 20x – 500 = 0
⇒ x(x + 25) – 20(x + 25) = 0
⇒ (x + 25)(x – 20) = 0
Either x + 25 = 0,
then x = –25,
but it is not possible as it is im negative.
or
x – 20 = 0,
then x = 20
∴ Petrol used by car B = 20 – 4 = 16 litres.
Question 21
The speed of a boat in still water is x km/hr and the speed of the stream is 3 km/hr.
(i) Write the speed of the boat upstream, in terms of X.
(ii) Write the speed of the boat downstream, in terms of x.
(iii) If the boat goes 15 km upstream and 22 km downstream in 5 hours, write an equation in x to represent the statement,
(iv) Solve the equation to evaluate x.
Answer :
let X be the speed of boat
in upstream 1/(X-15)……………1
in down stream 1/(X+22)………2
from 1 and 2
1/x – 15 + 1/X + 22 = 5houres
(X+22) + x – 15/(x-15)(X+22) = 5
2x+7/x² – (7)² = 5
2x+7/x² – 49 = 5
5(x² – 49) = 2x+7
5x² – 245 = 2x+7
5x² – 238 = 2x
5x² – 2x – 238 = 0
X= – b – or + ✓b² – 4ac/2a
=2 + – ✓{2}² – 4×5 × – 238/2 × 5
2 + – ✓4 – (- 4760)/10
2 + – ✓4 + 4760/10
2+-✓4764/10
2 + – 69/10
2 + 69/10 and 2-69/10
X = 7.1
Question 22
A booster pump can be used for filling as well as for emptying a tank. The capacity of the tank is 2400 m³. The emptying capacity of the tank is 10 m³ per minute higher than its filling capacity and the pump needs 8 minutes lesser to empty the tank than it needs to fill it. What is the filling capacity of the pump?
Answer :
Let the filling capacity of the pump =x m3/min.
Then the emptying capacity of the pump = (x+10) m3/min.
Time required for filling the tank = (2400/x) minutes.
Time required for emptying the tank = 2400/(x+10) minutes.
Pump needs 8 minutes lesser to empty the tank than it needs to fill it.
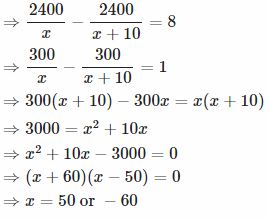
Since x can not be negative, x=50
filling capacity of the pump =50 m3/min.
Question 23
The hypotenuse of a right triangle is 20 m. If the difference between the lengths of other sides be 4 m, find the other sides.
Answer :
Let one side of the right-angled triangle be x m and the other side be (x+4)m
Pythagoras theorem,
20² = (x+4)² + x²
⇒400x² + 8x + 16 + x²
⇒ 2x² + 8x – 384=0
⇒x² +4x-192=0
⇒x² +16x-12x-192=0
⇒ x² (x+16)-12(x+16)=0
⇒(x+16)(x-12)=0
⇒ x= -16 or x=12
The value of x cannot be negative.
Therefore, the base is 12 m and the other side is {(12 + 4) = 16}
Question 24
The lengths of the sides of a right triangle are (2x- 1) m, (4x) m and (4x + 1) m, where x > 0. Find :
(i) the value of x,
(ii) the area of the triangle.
Answer :
the triangle is right-angled.
So, applying Pythagoras Theorem, which states that –
Here sides are given as,
(2x-1), 4x and (4x+1)m, where, x>0
=> 4x+1 is the longest side i.e. Hypotenuse.
Assume other sides of triangle to be Base or Height.
Let’s apply the Pythagoras Theorem,

This is the quadratic equation (having highest degree of 2).
So, roots of this equation are either 0 or 3. (x*(x-3) = 0)
As the root can’t be 0 as mentioned in the question.
So only root is 3 i.e. x = 3.
Let’s calculate the length of sides,
2x-1 = 2*3 – 1
= 5m
4x = 4*3
= 12m
4x+1 = 4*3 + 1
= 13m
So, sides are 5m, 12m and 13m.
Area of right angled triangle = 1/2 Base * height
= (12 * 5)/2
= 6*5
= 30 m²
Question 25
Two squares have sides x cm and (x+ 5) cm. The sum of their areas is 697 sq. cm.
(i) Express this as an algebraic equation in x.
(ii) Solve this equation to find the sides of the squares.
Answer :
Question 26
The area of a right-angled triangle is 96 m². If its base is three times its altitude, find the base.
Answer :
Let the altitude of the triangle be x m.
Therefore, the base will be 3x m.
Area of a triangle = 1/2 × Base × Altitude
∴ (1/2) × 3x × x = 96(∵Area = 96sqm)
⇒ x²/2=32
⇒ x² = 64
⇒ x = ±8
The value of x cannot be negative
Therefore, the altitude and base of the triangle are 8 m and (3 × 8 = 24m) respectively.
Question 27
The lengths of the parallel sides of a trapezium are (x + 8) cm and (2x + 3) cm, and the distance between them is (x + 4) cm. If its area is 590 cm, find the value of x.
Answer :

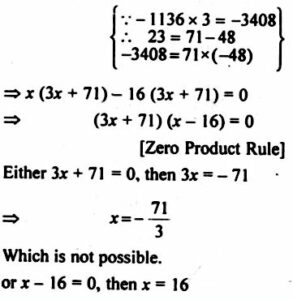
Question 28
The ratio between the length and the breadth of a rectangular field is 3 : 2. If only the length is increased by 5 metres, the new area of the field will be 2600 sq. metres. What is the breadth of the rectangular field ?
Answer :
Let the length and breadth be 3x and 2x.
Given,
New length= (3x+5)m
Area = l*b
2600=(3x+5)*2x
2600=6x²+10x
6x²+10x-2600=0
3x²+5x-1300=0
3x²+65x-60x-1300=0
x(3x+65)-20(3x-65)=0
(x-20)(3x+65)=0
Since, side can’t be negative…
x=20m
Breadth= 2*20= 40m
Please mark the answer brain liest
Question 29
The perimeter of a rectangular plot of land is 114 metres and its area is 810 square metres.
(i) Take the length of plot as x metres. Use the perimeter 114 m to write the value of the breadth in terms of x.
(ii) Use the values of length, breadth and area to write an equation in x.
(iii) Solve the equation to find the length and breadth of the plot.
Answer :
Perimeter = 2(Length + Breadth)
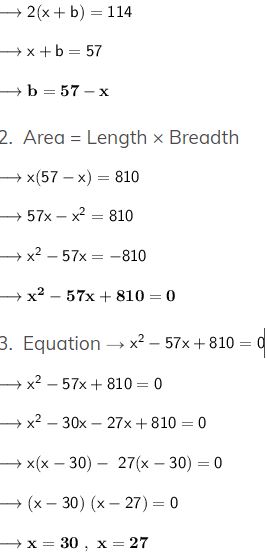
If length = 30m , breadth = 57 – 30 = 27m
If length = 27m , breadth = 57 – 27 = 30m
Question 30
A man buys an article for x and sells it for 56 at a gain of x %. Find the value of x.
Answer :
The gain percentage on the article given is x% and we have the formula of it:
Profit% =profit*100/cp
And Profit = SP – CP = 56-x
If we put the values in the formula then we get
x% = (56 – x)/x * 100
x = (56 – x)/x * 100
x²+100x-5600 = 0
x²+140x-40x-5600 = 0
x(x+140)-40(x+140) = 0
(x-40)(x+140) = 0
x = -140 and x = 40
Question 31
(i) Rs. 6400 were divided equally among x persons, Had this money been divided equally among (x + 14) persons, each would have got Rs. 28 less. Find the value of x.
(ii) Rs. 7500 were divided equally among a certain number of children. Had there been 20 less children, each would have received ? 100 more. Find the original number of children.
Answer :
(i)
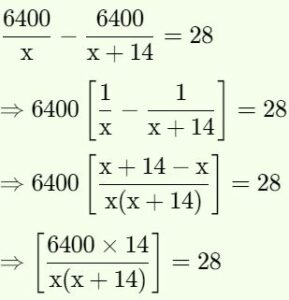
Let the original number of person be x, then 7500 divided equally between x person,
each one gets = 7500/x
7500 divided equally between x – 20 children
7500x = (x-20)(7500+100x)
75x = (x – 20)(75 + x)
75x = 75x + x2 – 1500 – 20x
x2 – 20x – 1500 = 0
x = 50 or x = -30 (not possible)
∴ original number of children = 50
Question 32
A shopkeeper buys x books for 720.
(i)Write the cost of 1 book in terms of x.
(ii) If the cost per book be R 5 less, the number of books that could be bought for 720 would be 2 more.
Write down the equation in x and solve it to find x.
Answer :
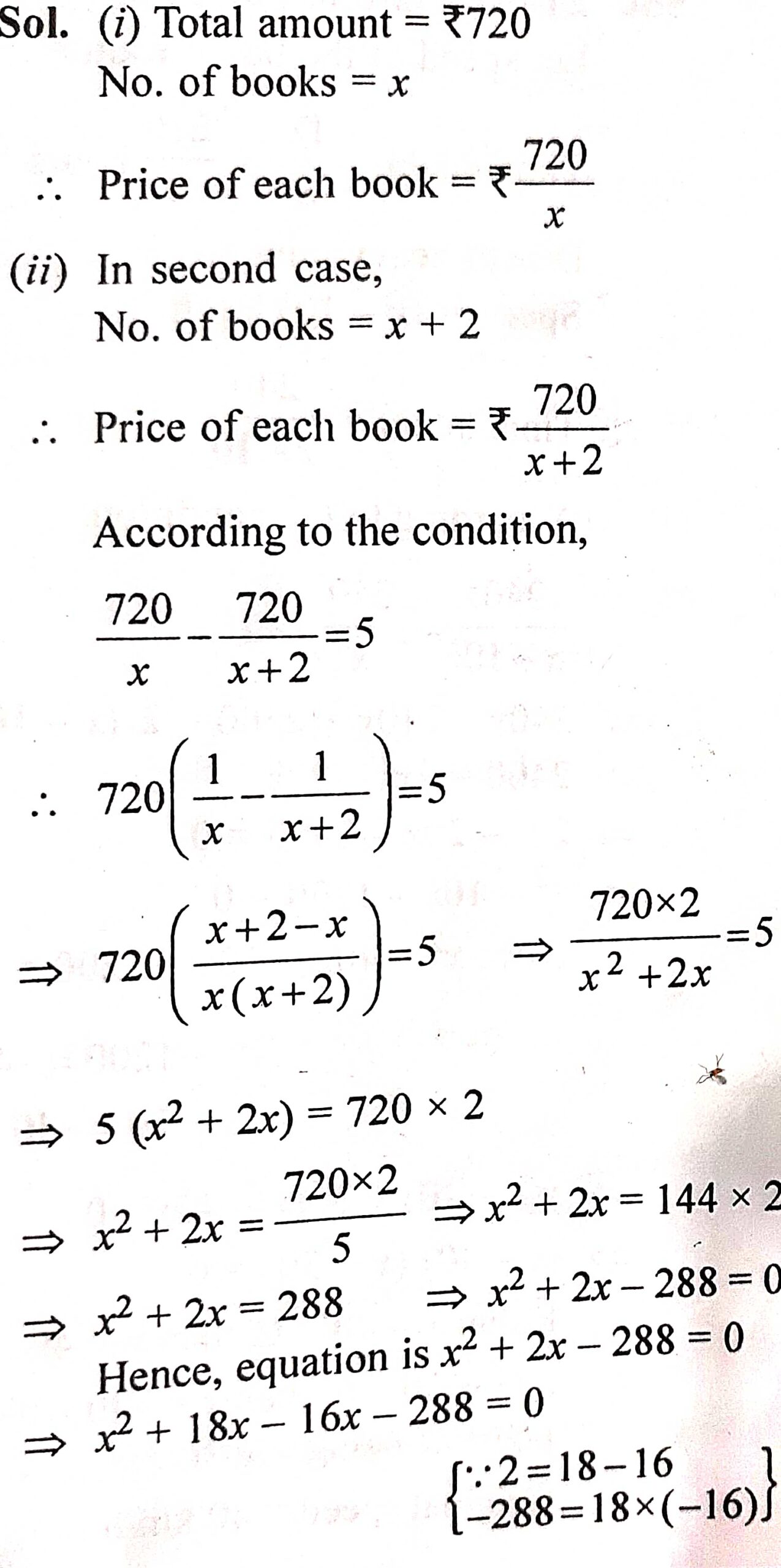
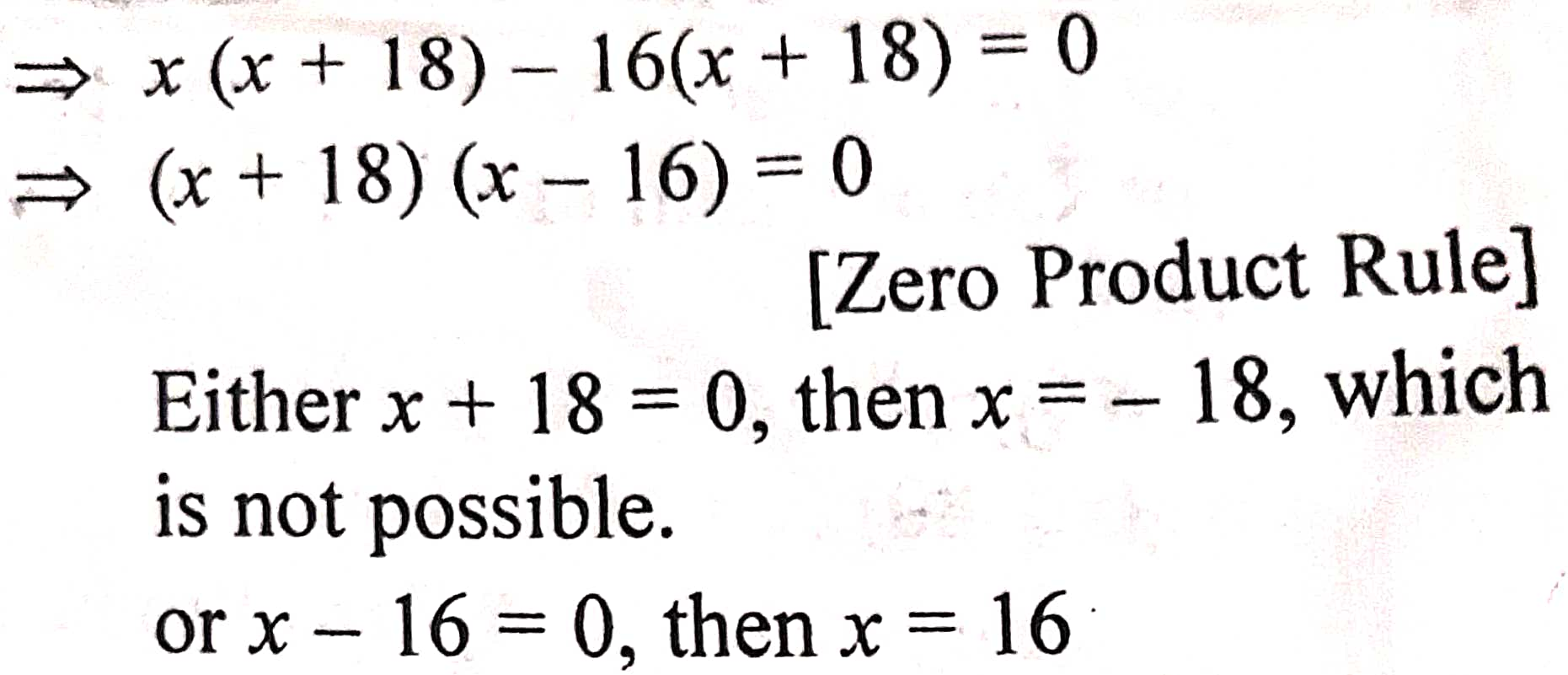
Question 33
A fruit-seller bought x apples for 1200.
(i) Write the cost price of each apple in terms of x.
(ii) If 10 of the apples were rotten and he sold each of the rest at Rs. 3 more than the cost price of each, write the selling price of (x – 10) apples.
(iii) If he made a profit of 60 in this transaction, form an equation in r and solve it to evaluate x.
Answer :
x apples are bought for 1200 Rs
(i) cost of per apple = (1200 / x ) Rs
(ii) 10 apples were rotten
hence, apple left for sale = x – 10
the cost at which apples will be sold is 3 more than the cost price of each apple
that will be = (1200/x) + 3 Rs
= ( 1200+3x) / x Rs
so, new selling price will be

(iii) it is given that the profit made during this transaction is 60 Rs
it means
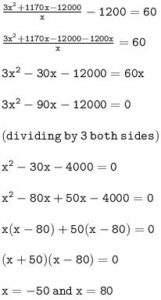
Cost should not be negative hence we will take value of x as
x = 80
Question 34
Some students planned a picnic. The budget for the food was Rs. 2400. As 8 of them failed to join the party, the cost of the food for each member increased by Rs. 50. Find how many students went to the picnic.
Answer :
Let,
total no. of students = x
and
cost of the food for each member = y
then,
x y = 2400 ……eqn (1)
x = 2400 / y …… eqn (2)
Now,
since 8 students failed to join the party
therefore,
no. of students = x – 8
also,
the cost of food is increased by ₹ 50
so,
increased cost of food for each = y + 50
then,
( x – 8 ) (y + 50 ) = 2400
xy + 50x – 8y –400 = 2400
using eqn (1)
2400 + 50x -8y -400 = 2400
50 x – 8 y – 400 = 0
using eqn (2)
50 (2400/y) – 8y = 400
( 120000 / y ) – 8y = 400
multiplying by y both sides
➛ 120000 – 8y² = 400 y
rearranging the terms
➛ 8 y² + 400 y – 120000 = 0
dividing by 8 both sides
➛ y² + 50 y – 15000 = 0
splitting the middle term
➛ y² + 150 y – 100 y – 15000 = 0
➛ y ( y + 150 ) – 100 ( y + 150 ) =0
➛ ( y-100) (y+150) = 0
so,
y = 100 and y = -150
negative value will be ignored so we will take
y = 100
putting this value in eqn (2)
x = 2400 / 100
x = 24
Question 35
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hours longer to cover the total distance. Assuming the uniform speed to be x km/h, form an equation and solve it to evaluate x.
Answer :
Time is taken by bus to cover the total distance with speed x km/h = 240/x
Time taken by bus to cover total distance with speed (x 10) km/h = 240/(x-10)
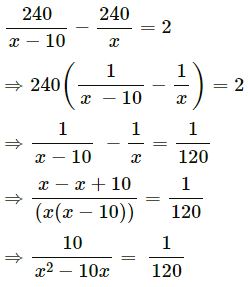
⇒ x2 – 10x = 1200
⇒ x2 – 10x – 1200 = 0
⇒ (x – 40)(x + 30) = 0
⇒ x- 40 = 0 or x = 30 = 0
⇒ x = 40 or x = -30
Since, the speed cannot be negative, the uniform speed is 40 km/h
Return to :- RS aggarwal Goyal Brothers Maths Solutions for ICSE Class-10
Thanks
Please share with your friends
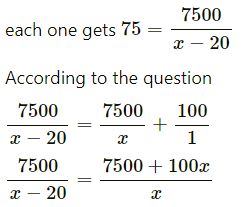
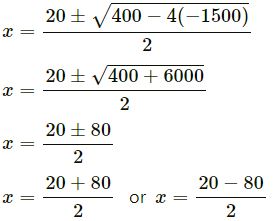



why are the answer not given please repair this complain it will be a good website if the answers are given
dear student/well wisher
upgrading for 2021-22 work is in progress
ok sir
can do it till bit fast
so that we can study
yes
please post the answers please
today it will be uploaded
plz post all answers back plz
Not able to see solutions for Problems On Quadratic Equations(Ch.6)
Book: RS Agarwal (Goyal brother prakashan)
dont worry uploaded again soon if unavailable
Please post again soon
ok
Pls post the answer key again not visible now pls help me as soon as possible
it is live now
ya we are unable to see the answer for quadratic equation word problem
it is live now
The questions solution are not showing of this topic
uploaded
stiil not able to see the solutions
loaded
No u didnt.
it is live now
no they aren’t sir
it is live
Unable to view the solutions from chp 5 to 27.pls check it
become live
not able to see any solutions please post them back soon.
now full chapter showing now please visit again
please post the pdf for chapter 6 maths goyal brothers
Problems on Quadratic Equations RS Aggarwal ICSE Class 10 it is live now
Please published class 10 icse R S Agarwal solutions chapter 6 and onwards.
uploading work is in progress
please post the pdf for 6th chapter
it is live now
please post the pdf for 6th chp
ok
pdf solutions not uploaded
ok very soon if not upload
Solutions are not visible pls fix this problem.
ok very soon
there are no answer for quadratic equation word problem
kindle pls see
we will look into matter
Please send all answers
live now
Please post the answers for this chapter and the others as soon as possible.
uploaded
it uploaded quadratic equation
The solutions are still not visible……is this some kind of a joke or probably we are blind!
now it is visible
can you please show where did you upload
ok at any rate today it will live
The boards are in 2 months pls upload fast as we have to prepare and then revise too
today will be uploaded
the answers are still not available
please fix the problem
today will be uploaded
pls post answers pls my exams tommorow
icse students assemble
updated now
plz post the answers of this chapter plz
today it will be uploaded
Please make available the answer now. Please i beg you.
uploaded
available now
It is not available please check and fix it asap sir
updated now
problems solved
Answer of Problem of Quadratic Equation are not been displayed
please check and resolve the problem
ok
Pls give the solutions.
uploaded
Answer are not given in L6:- problem on quadratic equations please upload fast
live now
Sir please upload the answers for this lesson
updated
Are yr answer kha hai answer kb ayenge ispe ye acchi site hoyegi.
wait 2 days more
only 2 day more
mistakely this chapter left
Please sur upload the solutions of this chapter as sonn as possible
uploaded
Where are the answers???
ans available in 2 day
Unable to view the solutions please can you upload it faster sir 🙏
Please upload it fast sir we need to revise as we have exams
today it will be uploaded
Plz upload the answers for the 6th chapter..🙏🙏🙏🙏
ok
thanks a lot sir it really helps me a lot to prepare for exams.
may god bless you.
thanks
thanks icse help, the solutions helped me for completing my notebook…..
thanks