Properties of Angles and Lines ICSE Class-6th Concise Selina Mathematics Solutions Chapter-25 (Including Parallel Lines). We provide step by step Solutions of Exercise / lesson-25 Properties of Angles and Lines (Including Parallel Lines) for ICSE Class-6 Concise Selina Mathematics.
Our Solutions contain all type Questions of Exe-25 A, Exe-25 B, Exe-25 C, Exe-25 D and Revision Exercise to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6.
Properties of Angles and Lines ICSE Class-6th Concise Selina Mathematics Solutions Chapter-25 (Including Parallel Lines)
–: Select Topics :–
Exercise – 25 A Properties of Angles and Lines (Including Parallel Lines) for ICSE Class-6th Concise Selina Mathematics Solutions
Question -1-.
Two straight lines AB and CD intersect each other at a point O and angle AOC = 50° ; find :
(i) angle BOD
(ii) ∠AOD
(iii) ∠BOC

Answer-1
(i)∠BOD = ∠AOC
(Vertically opposite angles are equal)
∴ ∠BOD =50°
(ii) ∠AOD
∠AOD + ∠BOD = 180°
∠AOD + 50° = 180° [From (i)]
∠AOD = 180°-50°
∠AOD = 130°
(iii) ∠BOC = ∠AOD
(Vertically opposite angles are equal)
∴ ∠BOC =130°
Question- 2.
The adjoining figure, shows two straight lines AB and CD intersecting at point P. If ∠BPC = 4x – 5° and ∠APD = 3x + 15° ; find :

(i) the value of x.
(ii) ∠APD
(iii) ∠BPD
(iv) ∠BPC
Answer-2
(i) 4x – 5 = 3x + 15 (∵ ∠CPB = ∠APD; opposite angles)
⇒ 4x – 3x = 15 + 5
⇒ x = 20
(ii) ∠APD = 3x + 15
= (3 × 20) + 15
= 60 + 15 = 75°
(iii) ∠BPD = 180 – ∠BPC
= 180 – (4x – 5)
= 180 – 4x + 5
= 185 – (4 × 20)
= 185 – 80 = 105°
(iv) ∠BPC = 4x – 5
= (4 × 20) – 5
= 80 – 5
= 75°
Question- 3.

Answer-3
Since, the exterior arms of the adjacent angles are in a straight line ; the adjacent angles are supplementary
∴ ∠AOB + ∠AOC = 180°
⇒ 68° + 3x – 20° = 180°
⇒ 3x = 180° + 20° – 68°
⇒ 3x = 200° – 68° ⇒ 3x =132°
x = 132⁄3 = 44°
Question -4.
Each figure given below shows a pair of adjacent angles AOB and BOC. Find whether or not the exterior arms OA and OC are in the same straight line.


Answer-4
(i) ∠AOB + ∠COB = 180°
Since, the sum of adjacent angles AOB and COB = 180°
(90° -x) + (90°+ x) = 180°
⇒ 90°-x + 90° + x = 180°
⇒ 180° =180°
The exterior arms. OA and OC are in the same straight line.
(ii) ∠AOB + ∠BOC = 97° + 83° = 180°
⇒ The sum of adjacent angles AOB and BOC is 180°.
∴ The exterior arms OA and OC are in the same straight line.
(iii)∠COB + ∠AOB = 88° + 112° = 200° ; which is not 180°.
⇒ The exterior amis OA and OC are not in the same straight line.
Question -5.
A line segment AP stands at point P of a straight line BC such that ∠APB = 5x – 40° and ∠APC = .x+ 10°; find the value of x and angle APB.
Answer-5
AP stands on BC at P and
∠APB = 5x – 40°, ∠APC = x + 10°

(i) ∵APE is a straight line
∠APB + ∠APC = 180°
⇒ 5x – 40° + x + 10° = 180°
⇒ 6x-30°= 180°
⇒6x= 180° + 30° = 210°
x = 2106° = 35°
(ii) and ∠APB = 5x – 40° = 5 x 35° – 40°
= 175 ° – 140° = 135°
Properties of Angles and Lines (Including Parallel Lines) Exercise-25 B for ICSE Class-6th Concise Selina Solutions
Question -1.
Identify the pair of angles in each of the figure given below :
adjacent angles, vertically opposite angles, interior alternate angles, corresponding angles or exterior alternate angles.


Answer-1
(a)
(i) Adjacent angles
(ii) Alternate exterior angles
(iii) Interior alternate angles
(iv) Corresponding angles
(v) Allied angles
(b)
(i) Alternate interior angles
(ii) Corresponding angles
(iii) Alternate exterior angles
(iv) Corresponding angles
(v) Allied angles.
(c)
(i) Corresponding
(ii) Alternate exterior
(iii) Alternate interior
(iv) Alternate interior
(v) Alternate exterior
(vi) Vertically opposite
Question -2.
Each figure given below shows a pair of parallel lines cut by a transversal For each case, find a and b, giving reasons.




Answer-2
(i) a + 140° = 180° (Linear pair)
∴ a = 180° – 140° = 40°
But b = a (alternate angles)
= 40°
∴ a = 40°, b = 40°
(ii) ∵ l || m and p intersects them
b + 60° = 180° (Linear pair)
∴ b = 180° – 60° = 120°
and a = 60° (corresponding angle)
∴ a = 60°, b = 120°
(iii) a = 110° (Vertically opposite angles)
b = 180° – a (Co-interior angles)
= 180° – 110° = 70°
(iv) a = 60° (Alternate interior angles)
b = 180° – a (Co-interior angles)
= 180° – 60° = 120°
(v) a = 72° (Alternate interior angles)
b = a (Vertically opposite angles)
i.e. b = 72°
(vi) b = 100° (Corresponding angles)
a = 180° – b (Linear pair of angles)
a = 180° – 100° = 80°
(vii) a = 180° – 130° = 50° (Co-interior angles)
b = 130° (Vertically opposite angles)
(viii) b = 62° (Corresponding angles)
a = 180° – b (Linear pairs of angles)
a = 180° – 62° = 118°
(viii) a = 180° – 90° (Linear pairs of angles)
= 90°
b = 90° (Corresponding angles)
Question -3.

Answer-3
l || m and p is their transversal and ∠1 = 120°
∠1 + ∠2 = 180° (Straight line angle)
∴ 120° + ∠2 = 180°
⇒ ∠2 = 180° – 120° = 60°
∴ ∠2 = 60°
But ∠1 = ∠3 (Vertically opposite angles)
∴ ∠3 = ∠1 = 120°
Similarly ∠4 = ∠2 (Vertically opposite angles)
∴ ∠4 = 60°
∠5 = ∠1 (Corresponding angles)
∴ ∠5 = 120°
Similarly ∠6 = ∠2 (Corresponding angles)
∴ ∠6 = 60°
∠7 = ∠5 (Vertically opposite angles)
∴ ∠7 = 120°
and ∠8 = ∠6 (Vertically opposite angles)
∴ ∠8 = 60°
Hence ∠2 = 60°, ∠3 = 120°, ∠4 = 60°,∠5 = 120°, ∠6 = 60°, ∠7 = 120° and ∠8 = 60°.
Question- 4.
In the figure given below, find the measure of the angles denoted by x,y, z,p,q and r.

Answer-4
x = 180 – 100 [L.P. of angles] = 80°
y = x [Alternate exterior angles]
= 80°
z = 100° [Corresponding angles]
p = x [Vertically opp. angles]
= 80°
q = 100° [Vertically opp. angles]
r = q [Corresponding angles]
= 100°
Question -5.
Using the given figure, fill in the blanks.

Answer-5
x = 60° [Corresponding angles]
z = x [Corresponding angles]
= 60°
p = z [Vertically opposite angle]
= 60°
q = 180 – P [Linear Pair of angles]
= 180 – 60 = 120°
r = 180 – x [Linear Pair of angles]
= 180 – 60 = 120°
s = r [Vertically opposite angle] = 120°
Question- 6.
In the given figure, find the angles shown by x,y, z and w. Give reasons.

Answer-6
x = 115° [Vertically of angles]
y = 70° [vertically opposite Angles]
z = 70° [Alternate interior angles]
w = 115° [Alternate interior angles]
Question -7.
Find a, b, c and d in the figure given below :

Answer-7
a = 130° [Vertically of angles]
b = 150° [vertically opposite Angles]
c = 150° [Alternate interior angles]
d = 130° [Alternate interior angles]
Question- 8.
Find x, y and z in the figure given below :

Answer-8
x = 180 – 75 = 105° [Co-interior angles]
y = 180 – x [Co-interior angles]
= 180 – 105 = 75°
z = 75° [Co-interior angles]
Concise Maths Selina Solutions of Exercise 25 C Properties of Angles and Lines (Including Parallel Lines) for ICSE Class-6th
Question- 1.
In your note-book copy the following angles using ruler and a pair compass only.

Answer-1
(i) Steps of Construction:
1. At point Q, draw line QR = OB.
2. With O as a centre, draw an arc of any suitable radius, to cut the arms of the angle at C and D.
3. With Q as a centre, draw the arc of the same size as drawn for C and D. Let this arc cuts line QR at point T.
4. In your compasses, take the distance equal to distance between C and D; and then with T as a centre, draw an arc which cuts the earlier arc at S.
5. Join QS and produce up to a suitable point P. ∠PQR so obtained, is the angle equal to the given ∠AOB.
(ii) Steps of Construction:
1. A t point E, draw line EF.
2. With E as centre, draw an arc of any suitable radius, to cut the amis of the angle at C and D.
3. With Q as a centre, draw the arc of the same size as drawn for C and D. Let this arc cuts line QR at point T.
4. In your compasses, take the distance equal to the distance between C and D; and then with T as a centre, draw an arc which cuts the earlier arc at S.
5. Join QS and produce up to a suitable point R ∠PQR, so obtained, is the angle equal to the given ∠DEE
(iii) Steps of Construction:
1. At point A draw line AB = QP
2. With Q as centre, draw an arc of any suitable radius, to cut the arms of the angle A + C and D.
3. With A as centre, draw the arc of the same size as drawn for C and D. Let this arc cuts line AB at D.
4. In your compasses, take the distance equal to distance between 7 and 5; and then with D as centre, draw an arc which cuts the earlier arc at E.
5. Join AE and produced up to a suitable point C. ∠BAC, so obtained is the angle equal to the given ∠PQR.
Question -2.
Construct the following angles, using ruler and a pair of compass only
(i) 60°
(ii) 90°
(iii) 45°
(iv) 30°
(v) 120°
(vi) 135°
(vii) 15°
Answer-2
(i) 60° Steps of Construction:
To construct an angle of 60°.

- Draw a line OA of any suitable length.
- At O, draw an arc of any size to cut OA at B.
- With B as a centre, draw the same size arc, to cut the previous arc at C.
- Join OC and extend up to a suitable point D, Then, ∠DOA = 60°.
(ii) 90° Steps of Construction:
To construct an angle of 90°.

- With O as a center, draw an arc to cut OA at B.
- With B as a centre, draw the same size arc to cut the previous arc at C.
- Again with C as centre and with the same radius, draw one more arc to cut the first arc at D.
- With C and D as centres, draw two arcs of equal radii to cut each other at point E.
- Join O and E, Then, ∠AOE = 90°.
(iii) 45°
Draw an angle of 90° as in the previous question and bisects it. Each angle so obtained will be 45°.

(iv) 30° Steps of construction:
To construct an angle of 30°.

- Draw a line OB of any suitable length.
- At O, draw an arc of any size to cut OB at D.
- With D as a centre, draw the same size arc, to cut the previous arc at C.
- Join OC and extend up to a suitable point A. Then, ∠AOB = 60°.
- Bisect this angle of get two angles each of 30°. Thus, ∠EOB = 30°.
(v) 120° Steps of construction:
To construct an angle of 120°.

- With centre O on the line OA, draw an arc to cut this line at C.
- With C as a centre, drawn the same size arc which cuts the first arc at point D.
- With D as a centre, draw one more arc of same size which cuts the first arc at E.
- Join OE and produce it up to point B. Then, ∠AOB = 120°
(vi) 135° Steps of construction:
To construct an angle of 135°.

- Draw an angle BOA = 90° at point O of given line AC.
- Bisect the angle BOC on the other side of OB, which is also 90°
- Thus, ∠BOD = ∠COD = 45°
And, ∠AOD = 90° + 45° = 135°
(vii) 15° Steps of construction:
To construct an angle of 15°.
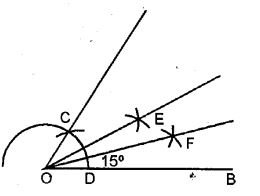
- Draw an angle of 60° as drawn above.
- Bisect this angle of get two angles each of 30°. Thus, ∠EOB = 30°
- Bisect this angle ∠EOB to get two angles each of 15°. ∠EOB = 15°.
Question -3.
Draw line AB = 6cm. Construct angle ABC = 60°. Then draw the bisector of angle ABC.
Answer-3
Steps of Construction:
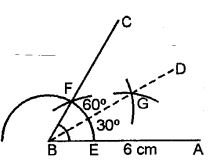
1. Draw a line segment AB = 6 cm.
2. With the help of compass construct ∠CBA = 60°.
3. Bisect ∠CBA, with the help of a compass, take any radius which meet line AB and BC at point E and F.
4. Now, with the help of compass take radius more than 12 of EF and draw two arcs from point E and F, which intersect both arcs at G, proceed BG toward D ∠DBA is bisector of ∠CBA.
Question -4.
Draw a line segment PQ = 8cm. Construct the perpendicular bisector of the line segment PQ. Let the perpendicular bisector drawn meet PQ at point R. Measure the lengths of PR and QR. Is PR = QR ?
Answer-4
Steps of Construction:
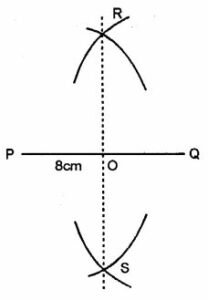
1. With P and Q as centers, draw arcs on both sides of PQ with equal radii. The radius should be more than half the length of PQ.
2. Let these arcs cut each other at points R and RS
3. Join RS which cuts PQ at D.
Then RS = PQ Also ∠POR = 90°.
Hence, the line segment RS is the perpendicular bisector of PQ as it bisects PQ at P and is also perpendicular to PQ. On measuring the lengths of PR = 4cm, QR = 4 cm Since PR = QR, both are 4cm each
∴ PR = QR.
Question -5.
Draw a line segment AB = 7cm. Mark a point Pon AB such that AP=3 cm. Draw perpendicular on to AB at point P.
Answer-5
1. Draw a line segment AB = 7 cm.

2. Out point from AB – AP =3cm
3. From point P, cut arc on out side of AB, E and F.
4. From point E & F cut arcs on both side intersection each other at C & D.
5. Join point P, CD.
6. Which is the required perpendicular.
Question -6.
Draw a line segment AB = 6.5 cm. Locate a point P that is 5 cm from A and 4.6 cm from B. Through the point P, draw a perpendicular on to the line segment AB.
Answer-6
Steps of Construction :
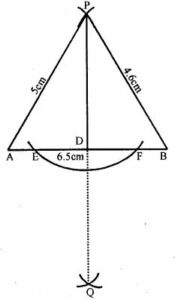
(i) Draw a line segment AB =6.5cm
(ii) With centre A and radius 5 cm, draw an arc and with centre B and radius 4.6 cm, draw another arc which intersects the first arc at P.
Then P is the required point.
(iii) With centre A and a suitable radius, draw an arc which intersect AB at E and F.
(iv) With centres E and F and radius greater than half of EF, draw the arcs which intersect each other at Q.
(v) Join PQ which intersect AB at D.
Then PD is perpendicular to AB
ICSE Class-6 Mathematics Exe-25 D Properties of Angles and Lines (Including Parallel Lines)
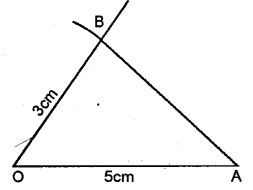
Question -1.
Draw a line segment OA = 5 cm. Use set-square to construct angle AOB = 60°, such that OB = 3 cm. Join A and B ; then measure the length of AB.
Answer-1
Measuring the length of AB = 4.4cm. (approximately)
Question- 2.
Draw a line segment OP = 8cm. Use set-square to construct ∠POQ = 90°; such that OQ = 6 cm. Join P and Q; then measure the length of PQ.
Answer-2
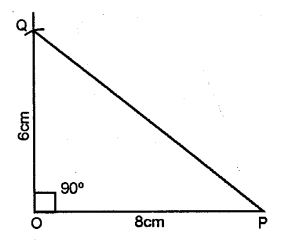
Measuring PQ = 10 cm
Question- 3.
Draw ∠ABC = 120°. Bisect the angle using ruler and compasses. Measure each angle so obtained and check whether or not the new angles obtained on bisecting ∠ABC are equal.
Answer-3
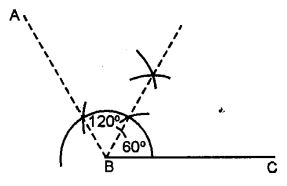
Measuring PQ = 60°
Yes, angles obtained in ∠ABC bisecting are equal.
Question -4.
Draw ∠PQR = 75° by using set- squares. On PQ mark a point M such that MQ = 3 cm. On QR mark a point N such that QN = 4 cm. Join M and N. Measure the length of MN.
Answer-4

Length of MN = 4.3 cm
Revision Exercise Properties of Angles and Lines (Including Parallel Lines) for ICSE Class-6th Concise Selina Mathematics Solutions
Question -1.
In the following figures, AB is parallel to CD; find the values of angles x, y and z :

Answer-1
(i) In the given figure,
AB || CD
and LM is its transversal
∴ ∠ALM = ∠LMN (Alternate angles)
⇒ ∠x = 105°
∴ x = 105°
Similarly AB || CD and LN is its transversal
∴ ∠BLN = ∠LNM (Alternate angles)
∴ ∠z = 60°
∴ z = 60°
But x + y + z = 180° (Straight line angles)
⇒ 105° + y + 60° = 180°
⇒ y + 165° = 180°
⇒ y = 180° – 165° = 15°
Hence x = 105°, y = 15° and z = 60°
(ii) In the given figure,
AB || CD
and MN is its transversal
∴ ∠LMN = ∠NMD (Alternate angles)
⇒ y = 45°
and AB || CD and LM is its transversal
∴ ∠ALM = ∠CMP (Corresponding angles)
⇒ 75° = x
∴ x = 75°
and ∠ALM = ∠LMD (Alternate angles)
⇒ 75° = z + 45°
⇒ z =75° – 45° = 30°
Hence x = 75°, y = 45° and z = 30°
Question -2.
In each of the following figures, BA is parallel to CD. Find the angles a, b and c:

Answer-2
(i)
In the given figure,
ABC is a triangle and CD || BA, BC is produced to E.
∠A = 60°, ∠B = 70°
∵ AB || DC and BE is its transversal
∴ ∠DCE = ∠ABC (Corresponding angles)
⇒ a = 70°
∴ a = 70°
Similarly, AB || DC and AC is its transversal
∴ ∠ACD = ∠BAC (Alternate angles)
⇒ b = 60°
∴ b = 60°
But a + b + c = 180° (Straight line angle)
⇒ 70° + 60° + c = 180°
⇒ 130° + c = 180°
⇒ c = 180° – 130° = 50°
Hence a = 70°, b = 60° and c = 50°
(ii) In the given figure,
ABC is a triangle and AB || DC and AC is its transversal.
∠BAC = ∠ACD (Alternate angles)
⇒ b = 65°
Again AB || DC and BCE is its transversal
∴ ∠ABC = ∠DCE
⇒ C = 70°
But ∠ACB + ∠ACD + ∠DCE = 180 (Straight line angle)
∴ a + 65° + 70° = 180°
⇒ a + 135° = 180°
⇒ a = 180° – 135° = 45°
Hence a = 45°, b = 65° and c = 70°
Question -3.
In each of the following figures, PQ is parallel to RS. Find the angles a, b and c:

Answer-3
(i) In the given figure,
PQ || RS, ∠B = 75°, ∠ACS = 140°
AB is its transversal
∴ ∠PAB = ∠ABC
⇒ a = 75°
Again PQ || RS and AC is its transversal
∴ ∠QAC + ∠ACS = 180° (Co-interior angles)
⇒ c + 140° = 180°
⇒ c = 180° – 140° = 40°
But a + b + c = 180° (Straight line angles)
∴ 75° + b + 40° = 180°
⇒ b + 115° = 180°
⇒ b = 180° – 115° = 65°
Hence a = 75°, b = 65°, c = 40°
(ii) In the given figure,
PQ || RS, ∠BAR = 63°, ∠CAS = 57°
AB is its transversal.
∴ ∠CBA = ∠BAR (Alternate angles)
⇒ a = 63°
∵ PQ || RS and CA is its transversal
∴ ∠QCA + ∠CAS = 180° (Co-interior angles)
⇒ b + 57° = 180°
⇒ b = 180° – 57° = 123°
But ∠CAS + ∠CAB + ∠BAR = 180° (Straight line angles)
∴ 57° + c + 63° = 180°
⇒ c + 120° = 180°
⇒ c = 180° – 120° = 60°
Hence a = 63°, b = 123°, c = 60°
Question- 4.
Two straight lines are cut by a transversal. Are the corresponding angles always equal?
Answer-4
If a transversal cuts two straight lines, their the corresponding angles are not equal unless the lines are not parallel. One in case of parallel lines, the corresponding angles are equal.
Question -5.
Two straight lines are cut by a transversal so that the co-interior angles are supplementary. Are the straight lines parallel?
Answer-5
A transversal intersects two straight lines and co-interior angles are supplementary
∴ By deflations, the lines will be parallel.
Question -6.
Two straight lines are cut by a transversal so that the co-interior angles are equal. What must be the measure of each interior angle to make the straight lines parallel to each other ?
Answer-6
A transversal intersects two straight lines and co-interior angles are equal to each other,
∵ The two straight lines are parallel Their sum of co-interior angles = 180°
But both angles are equal
∴ Each angle will be ..180⁄2…= 90…
Question- 7
In each case given below, find the value of x so that POQ is straight line


Answer-7
(i) POQ is a straight line.
In the given figure,
∵ POQ is a straight line
∴ ∠POL + ∠LOM + ∠MOQ = 180° (Straight line angles)
⇒ x + 20° + 2x – 30° + 3x – 50°= 180°
⇒ 6x + 20° – 80° = 180°
⇒ 6x – 60° = 180°
⇒ 6x = 180° + 60° = 240°
⇒ x = 240∘6
⇒ x = 40°
∴ x = 40°
(ii) ∵ POQ is a straight line
∴ ∠POL + ∠LOQ = 180°
⇒ 7x⁄11 +x=180∘
⇒ 7x+11x⁄11 =180°
⇒ 18x⁄11 =180°
⇒ x = 180°× 11⁄18 = 110°
∴ x = 110°
(iii) 5.5x + 15° = 180°
⇒ 5.5x = 180° – 15°
⇒ 5.5x = 165°
⇒ 18x⁄11=180°
⇒ x = 165⁄5.5 = 165×10⁄55 = 30°
∴ x = 30°
Question- 8.
in each case, given below, draw perpendicular to AB from an exterior point P

Answer-8
(i) Steps of Construction:
- From point P, draw an arc CD at line AB
- From point C and D draw arcs that intersect each other at point E, now draw PE, perpendicular to AB
(ii) Steps of construction:
- From point P, draw an arc CD at line AB.
- From point C and D draw arcs that intersect each other at point E, now draw PE, perpendicular to AB.
Question -9.
Draw a line segment BC = 8 cm. Using set-squares, draw ∠CBA = 60° and ∠BCA = 75°. Measure the angle BAC. Also measure the lengths of AB and AC.
Answer-9

Length AB = 11 cm
Length AC = 9.8 cm
∠BAC = 45°.
Question -10.
Draw a line AB = 9 cm. Mark a point P in AB such that AP=5 cm. Through P draw (using set-square) perpendicular PQ = 3 cm. Measure BQ.
Answer-10

BQ = 5 cm
Question- 11.
Draw a line segment AB = 6 cm. Without using set squares, draw angle OAB = 60° and angle OBA = 90°. Measure angle AOB and write this measurement.
Answer-11
Steps of construction:
- Draw a line segment AB = 6 cm
- At A, draw a ray making an angle of 60° with the help of a compass.
- At B, draw another ray making an angle of 90° which meet each other at O.
Now on measuring ∠AOB, it is 30°

Question- 12.
Without using set squares, construct angle ABC = 60° in which AB = BC = 5 cm. Join A and C and measure the length of AC.
Answer-12
Steps of Construction:
- Draw an angle ABC = 60
Such that AB = BC = 5 cm - Join AC, on measuring, the length of AC = 5 cm.

End of Properties of Angles and Lines Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -6
Thanks