Quadratic Equations MCQs for ICSE Class-10 Maths

Quadratic Equations MCQs for ICSE Class-10 Maths for Sem-1. These MCQ / Objective Type Questions of Quadratic Equations is based on latest reduced syllabus according 2021-22 session on bifurcated pattern. Main motto of MCQ Type Question is cracking the next upcoming exam of council. Visit official website CISCE for detail information about ICSE Board Class-10 Maths

MCQs of Quadratic Equations for ICSE Class-10 Maths

Board	ICSE
Class	10th ( x )
Subject	Maths
Chapter	Quadratic Equations
Syllabus	on bifurcated syllabus (after reduction)
bifurcated pattern	Semester-1
Session	2021-22
Topic	MCQ / Objective Type Question

Multiple Choice Questions (MCQs) of Quadratic Equations for ICSE Class-10 Maths

Question :-1 Which of the following is not a quadratic equation

(a) x² + 3x – 5 = 0
(b) x² + x³ + 2 = 0
(c) 3 + x + x² = 0
(d) x² – 9 = 0

Answer: (b) x² + x³ + 2 = 0
Hint : Since it has degree 3.

Question :-2 The equation (x – 2)² + 1 = 2x – 3 is a
(a) linear equation
(b) quadratic equation
(c) cubic equation
(d) bi-quadratic equation

Answer: (b) quadratic equation
hint We have (x – 2)² + 1 = 2x – 3
⇒ x² + 4 – 2 × x × 2 + 1 = 2x – 3
⇒ x² – 4x + 5 – 2x + 3 = 0
∴ x² – 6x + 8 = 0, which is a quadratic equation.

Question :-3 The roots of the quadratic equation 6x² – x – 2 = 0 are

(a) −1/2, x = 2/ 3
(b) −1/2, x = – 2/ 3
(c) −1/2, x = –2/ 3
(d) 1/2, x = 2/ 3

Answer- (a) −1/2, x = 2/ 3

hint : We have 6×2 – x – 2 = 0
⇒ 6x² + 3x-4x-2 = 0
⇒ 3x(2x + 1) -2(2x + 1) = 0
⇒ (2x + 1) (3x – 2) = 0
⇒ 2x + 1 = 0 or 3x – 2 = 0
∴ x =−1/2, x = 2/ 3

Question :-4 The quadratic equation whose one rational root is 3 + √2 is
(a) x² – 7x + 5 = 0
(b) x² + 7x + 6 = 0
(c) x² – 7x + 6 = 0
(d) x² – 6x + 7 = 0

Answer: (d) x² – 6x + 7 = 0
hint ∵ one root is 3 + √2
∴ other root is 3 – √2
∴ Sum of roots = 3 + √2 + 3 – √2 = 6
Product of roots = (3 + √2)(3 – √2) = (3)² – (√2)² = 9 – 2 = 7
∴ Required quadratic equation is x² – 6x + 7 = 0

Question :-5 . The equation 2x² + kx + 3 = 0 has two equal roots, then the value of k is
(a) ±√6
(b) ± 4
(c) ±3√2
(d) ±2√6

Answer:(d) ±2√6
hint: Here a = 2, b = k, c = 3
Since the equation has two equal roots
∴ b² – 4AC = 0
⇒ (k)² – 4 × 2 × 3 = 0
⇒ k² = 24
⇒ k = ± √24
∴= ± 2√6

Question -6 The difference between the squares of two numbers is 45. The square of the smaller number is 4 times the larger number. the numbers are

(a) 9, 6
(b) 3, 6
(c) 3, 9
(d) 9, 3

Answer- (a) 9, 6

Let the larger number = x
then smaller number = y
Now according to the condition,

x² – y² = 45 … (i)

y² = 4x … (ii)

substitute the value of y in equation (i),

x² – 4x = 45

x² – 4x – 45 = 0

on factorize,

x² – 9x + 5x – 45 = 0

x(x – 9) + 5 (x – 9) = 0

(x – 9) (x + 5) = 0

either (x – 9) = 0 or (x + 5) = 0

so x = 9 or x = -5

When x = 9, then

The larger number = x = 9

and Smaller number = y => y² = 4x

y = √4x = √4(9) = √36 = 6

When x = -5, then

The larger number = x = -5

Smaller number = y => y² = 4x

y = √4x = √4(-5) = √-20 (which is not possible)

hence The value of x and y are 9, 6.

Question :-7 One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son’s age. Their present ages are
(a) 7 years, 49 years
(b) 5 years, 25 years
(c) 1 years, 50 years
(d) 6 years, 49 years

Answer: (a) 7 years, 49 years

Question :-8 The sum of the squares of two consecutive natural numbers is 313. The numbers are
(a) 12, 13
(b) 13,14
(c) 11,12
(d) 14,15

Answer: (a) 12, 13

Question :-9 A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.

(A) 3

(B) 8

(D) 7

Answer: (B) 8

hint

Let the number be x

Then according question,

x + 12 = 160/x

x² + 12x – 160 = 0

x² + 20x – 8x – 160 = 0

(x + 20) (x – 8) = 0

x = -20, 8

Question :-10 The product of two successive integral multiples of 5 is 300. Then the numbers are:

(a) 25, 30

(b) 10, 15

(d) 15, 20

Answer: (d) 15, 20

hint

Let the consecutive integral multiple be 5n and 5(n + 1) where n is a positive integer.

According to the question:

5n × 5(n + 1) = 300

⇒ n² + n – 12 = 0

⇒ (n – 3) (n + 4) = 0

⇒ n = 3 and n = – 4.

As n is a positive natural number so n = – 4 will be discarded.

Therefore the numbers are 15 and 20.

Question :-11 If p²x² – q² = 0, then x =?

(A) ± q/p

(B) ±p/q

(D) q

Answer: (A) ± q/p

hint:

p²x² – q² = 0

⇒p²x² = q²

⇒x = ±p/q

Question :-12 Rohini had scored 10 more marks in her mathematics test out of 30 marks, 9 times these marks would have been the square of her actual marks. How many marks did she get in the test?

(a) 14

(b) 16

(d) 18

Answer: (c) 15

hint

Let her actual marks be x

Therefore,

9 (x + 10) = x²

⇒x² – 9x – 90 = 0

⇒x² – 15x + 6x – 90 = 0

⇒x(x – 15) + 6 (x – 15) = 0

⇒(x + 6) (x – 15) = 0

Therefore x = – 6 or x =15

Since x is the marks obtained, x ≠ – 6. Therefore, x = 15.

Question :-13 A train travels at a certain average speed for a distance of 63 km and then travels a distance of 72 km at an average speed of 6 km/h more than its original speed. If it takes 3 hours to complete the total journey, what is its original average speed?

(a) 42 Km/hr

(b) 40 Km/hr

(d) 42.5 Km/hr

Answer: (a) 42 Km/hr

Question :-14 The sum of two numbers is 27 and product is 182. The numbers are:

(a) 12 and 13

(b) 13 and 14

(d) 13 and 24

Answer: (b) 13 and 14

Hint: Let x is one number

Another number = 27 – x

Product of two numbers = 182

x(27 – x) = 182

⇒ x² – 27x – 182 = 0

⇒ x² – 13x – 14x + 182 = 0

⇒ x(x – 13) -14(x – 13) = 0

⇒ (x – 13)(x -14) = 0

⇒ x = 13 or x = 14

Question :-15 The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, the other two sides of the triangle are equal to:

(a) Base=10cm and Altitude=5cm

(b) Base=12cm and Altitude=5cm

(d) Base=12cm and Altitude=10cm

Answer: (b) Base=12cm and Altitude=5cm

Hint Let the base be x cm.

Altitude = (x – 7) cm

In a right triangle,

Base² + Altitude² = Hypotenuse² (From Pythagoras theorem)

∴ x² + (x – 7)² = 13²

By solving the above equation, we get;

⇒ x = 12 or x = – 5

Since the side of the triangle cannot be negative.

Therefore, base = 12cm and altitude = 12-7 = 5cm

Question :-16 The roots of quadratic equation 2x² + x + 4 = 0 are:

(a) Positive and negative

(b) Both Positive

(d) No real roots

Answer: (d) No real roots

Hint: 2x² + x + 4 = 0

⇒ 2x² + x = -4

Dividing the equation by 2, we get

⇒ x² + 1/2x = -2

⇒ x² + 2 × x × 1/4 = -2

By adding (1/4)² to both sides of the equation, we get

⇒ (x)² + 2 × x × 1/4 + (1/4)² = (1/4)² – 2

⇒ (x + 1/4)² = 1/16 – 2

⇒ (x + 1/4)2 = -31/16

Question :-17 The sum of the reciprocals of Rehman’s ages 3 years ago and 5 years from now is 1/3. The present age of Rehman is:

(a) 7

(b) 10

(d) 6

Answer: (a) 7

Hint: Let, x is the present age of Rehman

Three years ago his age = x – 3

Five years later his age = x + 5

Given, the sum of the reciprocals of Rehman’s ages 3 years ago and after 5 years is equal to 1/3.

∴ 1/x-3 + 1/x-5 = 1/3

(x+5+x-3)/(x-3)(x+5) = 1/3

(2x+2)/(x-3)(x+5) = 1/3

⇒ 3(2x + 2) = (x-3)(x+5)

⇒ 6x + 6 = x² + 2x – 15

⇒ x² – 4x – 21 = 0

⇒ x² – 7x + 3x – 21 = 0

⇒ x(x – 7) + 3(x – 7) = 0

⇒ (x – 7)(x + 3) = 0

⇒ x = 7, -3

We know age cannot be negative, hence the answer is 7

Question :-18 A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.

(a) 30 km/hr

(b) 40 km/hr

(d) 60 km/hr

Answer: (b) 40 km/hr

Hint: Let x km/hr be the speed of train.

Time required to cover 360 km = 360/x hr.

As per the question given,

⇒ (x + 5)(360-1/x) = 360

⇒ 360 – x + 1800-5/x = 360

⇒ x² + 5x + 10x – 1800 = 0

⇒ x(x + 45) -40(x + 45) = 0

⇒ (x + 45)(x – 40) = 0

⇒ x = 40, -45

Negative value is not considered for speed hence the answer is 40km/h

Question :-19 If one root of equation 4x²-2x+k-4=0 is reciprocal of the other. The value of k is:

(a) -8

(b) 8

(d) 4

Answer: (b) 8

Hint: If one root is reciprocal of others, then the product of roots will be:

α x 1/α = (k-4)/4

k-4=4

k=8

Question :-20 Which one of the following is not a quadratic equation?

(a) (x + 2)² = 2(x + 3)

(b) x² + 3x = (–1) (1 – 3x)²

(d) x³ – x² + 2x + 1 = (x + 1)³

Answer: (c) (x + 2) (x – 1) = x² – 2x – 3

Hint

We know that the degree of a quadratic equation is 2.

By verifying the options,

(a) (x + 2)² = 2(x + 3)

x² + 4x + 4 = 2x + 6

x² + 2x – 2 = 0

This is a quadratic equation.

(b) x² + 3x = (–1) (1 – 3x)²

x² + 3x = -1(1 + 9x² – 6x)

x² + 3x + 1 + 9x² – 6x = 0

10x² – 3x + 1 = 0

This is a quadratic equation.

x² + x – 2 = x² – 2x – 3

x² + x – 2 – x² + 2x + 3 = 0

3x + 1 = 0

This is not a quadratic equation

Question :-21 The quadratic equation 2x² – √5x + 1 = 0 has

(a) two distinct real roots

(b) two equal real roots

(d) more than 2 real roots

Answer: (c) no real roots

Hint

Given,

2x² – √5x + 1 = 0

Comparing with the standard form of a quadratic equation,

a = 2, b = -√5, c = 1

Now,

b² – 4ac = (-√5)² – 4(2)(1)

= 5 – 8

= -3 < 0

Therefore, the given equation has no real roots.

Question :-22 The equation (x + 1)² – 2(x + 1) = 0 has

(a) two real roots

(b) no real roots

(d) two equal roots

Answer: (a) two real roots

Hint

(x + 1)² – 2(x + 1) = 0

x² + 1 + 2x – 2x – 2 = 0

x² – 1 = 0

x² = 1

x = ± 1

Question :-23 The quadratic formula to find the roots of a quadratic equation ax² + bx + c = 0 is given by

(a) [-b ± √(b²-ac)]/2a

(b) [-b ± √(b²-2ac)]/a

(d) [-b ± √(b²-4ac)]/2a

Answer: (d) [-b ± √(b²-4ac)]/2a

Hint

The quadratic formula to find the roots of a quadratic equation ax² + bx + c = 0 is given by [-b ± √(b²-4ac)]/2a.

Question :-24 The quadratic equation x² + 7x – 60 has

(a) two equal roots

(b) two real and unequal roots

(b) no real roots

Answer: (b) two real and unequal roots

Hint

Given,

x² + 7x – 60 = 0

Comparing with the standard form,

a = 1, b = 7, c = -60

b² – 4ac = (7)² – 4(1)(-60) = 49 + 240 = 289 > 0

Therefore, the given quadratic equation has two real and unequal roots

(b) b² – 4ac = 0

(d) b² – ac < 0

Answer: (c) b² – 4ac < 0

Hint A quadratic equation ax²+ bx + c = 0 has no real roots, if b² – 4ac < 0. That means, the quadratic equation contains imaginary roots

Question :-25 Which of the following is not a quadratic equation ?

(a) (x + 2)² = 2(x + 3)
(b) x² + 3x = ( – 1) (1 – 3x)
(c) (x + 2) (x – 1) = x² – 2x – 3
(d) x³ – x² + 2x + 1 = (x + 1)³

Answer -(d) x³ – x² + 2x + 1 = (x + 1)³

Hint

(a) (x + 2)² = 2(x + 3)
⇒ x² + 4x + 4 = 2x + 6
⇒ x² + 4x – 2x + 4 – 6 = 0
⇒ x² + 2x – 2
It is a quadratic equation.

(b) x² + 3x = ( – 1) (1 – 3x)
⇒ x² + 3x = –1 + 3x
⇒ x² + 1 = 0
it is also quadratic equation.

(c)(x + 2) (x – 1) = x² – 2x – 3

x² – x + 2x – 2 = x² – 2x – 3
x² – x² + x + 2x – 2 + 3 = 0
⇒ 3x + 1 = 0
It is not a quadratic equation.

(d) x³ – x² + 2x + 1 = (x + 1)³

= x³ + 3x² + 3x + 1
x³ – x²+ 2x + 1
3x² + x²– 2x – 1 + 3x + 1 = 0
⇒ 4x² + x = 0
It is a quadratic equation

Question :-26 The roots of the equation x² – 3x – 10 = 0 are

(a) 2,- 5
(b) – 2, 5
(c) 2, 5
(d) – 2, – 5

Answer-(b) – 2, 5

Hint

x² – 3x – 10 = 0

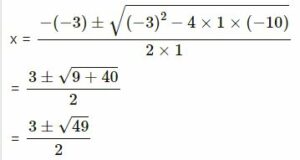
either

= (3+7)/ 2

∴ x = 10/2 = 5
or
x = (3-7)/2
=-4/2

= –2

x = 5, – 2 or – 2, 5 (b)

Question :-27 The value(s) of k for which the quadratic equation 2x² – kx + k = 0 has equal roots is (are)

(a) 0 only
(b) 4
(c) 8 only
(d) 0, 8

Answer-(d) 0, 8

Hint

2x² – kx + k = 0
a = 2, b = -k, c = k
∴ b² – 4ac
= (-k)² – 4 x 2 x 4
= k² – 8k
∴ Roots are equal.
∴ b² – 4ac = 0
k² – 8k = 0
⇒ k(k – 8) = 0
Either k = 0
or
k – 8 = 0,
then k = 8
k = 0, 8.
So option (d) is correct

Question :-28 If the equation 3x² – kx + 2k =0 roots, then the the value(s) of k is (are)

(a) 6
(b) 0 Only
(c) 24 only
(d) 0

Answer (d) 0

Hint

3x² – kx + 2k = 0
Here, a = 3, b = -k, c = 2k

Question :-29 If the equation {k + 1)x² – 2(k – 1)x + 1 = 0 has equal roots, then the values of k are

(a) 1, 3
(b) 0, 3
(c) 0, 1
(d) 0, 1

Answer -(b) 0, 3

Hint

(k + 1)x² – 2(k – 1)x + 1 = 0
Here, a = k + 1, b = -2(k – 1), c = 1
∴ b² – 4ac
= [–2(k –- 1)]² – 4(k + 1)(1)
= 4(k² – 2k + 1) – 4k – 4
= 4k² – 8k + 4 – 4k – 4
= 4k² – 12k
∵ Roots are equal.
∴ b² – 4ac = 0
∴ 4k² – 12k = 0
4k(k – 3) = 0
⇒ 4k(k – 3) = 0
⇒ k(k – 3) = 0
Either k = 0
or
k – 3 = 0,
then k = 3
k = 0, 3