Ratio and Proportion Class 6 RS Aggarwal Exe-8B Goyal Brothers ICSE Maths Solutions Ch-8. In this article you will learn about PROPORTION . Visit official Website CISCE for detail information about ICSE Board Class-6 Mathematics.
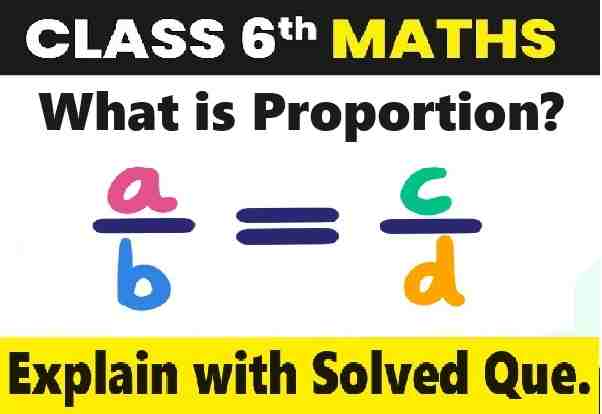
Ratio and Proportion Class 6 RS Aggarwal Exe-8B Goyal Brothers ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 6th |
| Ch-8 | Ratio and Proportion |
| Writer | RS Aggrawal |
| Book Name | Foundation |
| Topics | Solution of Exe-8b |
| Academic Session | 2024 – 2025 |
PROPORTION
Proportion is an equation that defines that the two given ratios are equivalent to each other. In other words, the proportion states the equality of the two fractions or the ratios. In proportion, if two sets of given numbers are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other
Proportion Formula
let us assume that, in proportion, the two ratios are a : b & c : d. The two terms ‘b’ and ‘c’ are called ‘mean term,’ whereas the terms ‘a’ and ‘d’ are known as ‘extremes or extreme terms.’ If a/b = c/d then a : b :: c : d
Exercise- 8B
(Ratio and Proportion Class 6 RS Aggarwal Exe-8B Goyal Brothers ICSE Maths Solutions Ch-8)
Que-1: Verify that :
(i) 12:18 = 8:12 (ii) 81kg : 45kg = 18men : 10men (iii) {3*(1/3)}:{2*(1/2)} = 12:9 (iv) 6:45 ≠ 4.8 : 3.6
Sol: (i) 12/18
= (12÷6)/(18÷6) = (2/3)×(4/4)
= 8/12 Hence Proved.
(ii) 81 kg : 45 kg : : 18 men : 10 men
or 81:45::18:10
Product of means = 45 × 18 = 810
Product of extremes = 81 × 10 = 810
Product of means = Product of extremes
Hence, (T).
(iii) L.H.S = (3+1/3):(2+1/2)
= (10/3):(5/2)
= 4:3
= (4 X 3)/(3 X 3) = 12/9
= 12:9 = R.H.S(VERIFIED)
(iv) 6/45 is not equal 4.8/3.6
2/15 is not equal 2.4/1.8
2/15 is not equal 1.2/0.9
2/15 is not equal 12/10/9/10
2/15 is not equal 12/10×10/9
2/15 is not equal 4/3 then proof that is not equal
Que-2: Which of the following numbers are in proportion.
(i) 30, 42, 5, 7 (ii) 4,11,22,33 (iii) 9,13,10,14 (iv) 16,18,24,27
Sol: (i) 30 1st term, 42 2nd term, 5 3rd term, 7 4th term
therefore 1st term × 4th term = 2nd term × 3rd term
= 30×7= 42×5
= 210 = 210
= L.H.S = R.H.S
(ii) 4 1st term, 11 2nd term, 22 3rd term, 33 4th term
therefore 1st term × 4th term = 2nd term × 3rd term
= 4×33 = 11×22
= 132 = 232
= L.H.S ≠ R.H.S
(iii) 9 1st term, 13 2nd term, 10 3rd term, 14 4th term
therefore 1st term × 4th term = 2nd term × 3rd term
= 9×14 = 13×10
= 126 = 130
= L.H.S ≠ R.H.S
(iv) 16 1st term, 18 2nd term, 24 3rd term, 27 4th term
therefore 1st term × 4th term = 2nd term × 3rd term
= 16×27 = 18×24
= 432 = 432.
= L.H.S = R.H.S
Que-3: Find the value of x in each of the following proportions.
(i) 36:81 :: x:63 (ii) 27:x :: 63:84 (iii) x:92 :: 87:116 (iv) 45:x :: 25:35
Sol: (i) 36:81 :: x:63
36/81 = x/63
x = (36×63)/81
x = 28.
(ii) 27:x :: 63:84
27/x = 63/84
x = (27×84)/63
x = 36.
(iii) x:92 :: 87:116
x/92 = 87/116
x = (87×92)/116
x = 69
(iv) 45:x :: 25:35
45/x = 25/35
x = (45×35)/25
x = 63.
Que-4: In a proportion, the 1st, 2nd and 4th terms are 32, 112 and 217 respectively. Find the 3rd terms.
Sol: Let the third term be x
Therefore, 32 : 112 :: x : 217
so, 32/112 = x/217
x = (32×217)/112
x = 62
So, the third term is 62.
Que-5: In a proportion, the 1st, 3rd and 4th terms are 51, 81 and 108 respectively. Find the 2nd term.
Sol: Let the second term be x.
Then, 51 : x : : 81 : 108
81x = 51×108
x = (51×108)/81
x = 68.
Que-6: The income of Ruchi and Rajan are in the ratio 4:7. If Ruchi earns Rs16800 per month, how much does Rajan earn per month ?
Sol: Ruchi’s income : Rajan’s income = 4 : 7
We know Ruchi’s income is ₹16,800, so let’s represent Rajan’s income as x.
We can set up the proportion:
4/7 = 16800/x
To solve for x, we can cross-multiply:
4x = 7 × 16800
4x = 117600
Now, divide both sides by 4:
x = 117600 ÷ 4
x = 29400
Que-7: An electric pole casts a shadow of length 20 metres at a time when a tree 6 metres high casts a shadow of length 8 metres. Find the height of the pole.
Sol: Let the height of the pole = x m
Then, we have:
x : 20 :: 6 : 8
Now, we know:
Product of extremes = Product of means
8x = 20 × 6
x = 120/8 = 15
Hence, the height of the pole is 15 m.
Que-8: The ratio of copper and zinc in an alloy is 9:5. If the weight of zinc in the alloy is 9.5g, what is the weight of copper in it ?
Sol: Ratio of copper to zinc = 9:5
Weight of zinc = 9.5 g
Let the weight of copper be x g.
x/9.5 = 9/5
x = (9.5×9)/5
x = 85.5/5
x = 7.1 g.
Que-9: The ratio of length and the breadth of a rectangular plot is 9:5. If its breadth is 60m, find its length.
Sol: Ratio of length and breath of a rectangle is 9:5
breath is 60m
Assume that length and breadth of rectangle are 9x m and 5x m respectively as ratio is 9 : 5
Equate 5x breadth with given breadth 60 m and solve for x
5x = 60
=> x = 12
Substitute x= 12 in length 9x and calculate the length
Length = 9x
Length = 9 * 12
Length = 108 m
–: Ratio and Proportion Class 6 RS Aggarwal Exe-8B Goyal Brothers ICSE Maths Solutions Ch-8 :–
Return to :- ICSE Class -6 RS Aggarwal Goyal Brothers Math Solutions
Thanks
Please share with yours friends if helpful


