ML Aggarwal Rectilinear Figures Exe-13.1 Class 9 ICSE Maths Solutions

ML Aggarwal Rectilinear Figures Exe-13.1 Class 9 ICSE Maths Solutions Ch-13. Step by Step Solutions of Exercise-13.1 Rectilinear Figures of ML Aggarwal for ICSE Class 9th Mathematics Questions. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Rectilinear Figures Exe-13.1 Class 9 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	9th
Chapter-13	Rectilinear Figures
Topics	Solution of Exe-13.1 Questions
Academic Session	2024-2025

Rectilinear Figures

ML Aggarwal Rectilinear Figures Exe-13.1 Class 9 ICSE Maths Solutions Ch-13.

Question 1. If two angles of a quadrilateral are 40° and 110° and the other two are in the ratio 3 : 4, find these angles.

Answer :  Sum of all four angles of a quadrilateral = 360°

Sum of two given angles = 40° + 110° = 150°

So, the sum of remaining two angles = 360° – 150° = 210°

Ratio in these angles = 3 : 4

Third angle = (210° ×3)/(3 + 4)

= (210° ×3)/7

= 90°

Fourth angle

= (210° ×4)/(3 + 4)

= (210° ×4)/7

= 120°

Question 2. If the angles of a quadrilateral, taken in order, are in the ratio 1 : 2 : 3 : 4, prove that it is a trapezium.

Answer : In trapezium ABCD in which

∠A : ∠B : ∠C : ∠D = 1 : 2 : 3 : 4

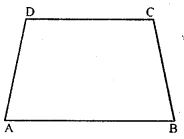
The sum of angles of the quad. ABCD = 360°

∠A = (360° ×1)/10 = 36°

∠B = (360° ×2)/10 = 72°

∠C = (360° ×3)/10 = 108°

∠D = (360° ×4)/10 = 144°

∠A + ∠D = 36° + 114° = 180°

Since, the sum of angles ∠A and ∠D is 180° and these are co-interior angles

Thus, AB || DC

Hence, ABCD is a trapezium.

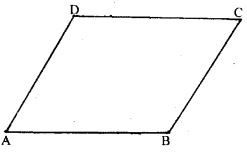
Question 3. If an angle of a parallelogram is two-thirds of its adjacent angle, find the angles of the parallelogram.

Answer :  Here ABCD is a parallelogram.

Let ∠A = x°

Then, ∠B = (2x/3)°

∠A + ∠B = 180° (As the sum of adjacent angles in a parallelogram is 180°)

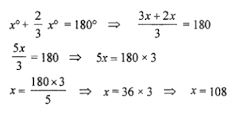
Therefore,

∠A = 108°

∠B = 2/3 ×108^o = 2 ×36° = 72°

⇒ ∠B = ∠D = 72° (opposite angles in a parallelogram is same)

Also,

∠A = ∠C = 108° (opposite angles in a parallelogram is same)

Hence, angles of parallelogram are 108°, 72°, 108° and 72°.

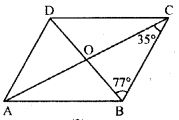
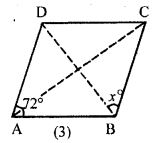
Question 4. (a) In figure (1) given below, ABCD is a parallelogram in which ∠DAB = 70°, ∠DBC = 80°. Calculate angles CDB and ADB.(b) In figure (2) given below, ABCD is a parallelogram. Find the angles of the AAOD.(c) In figure (3) given below, ABCD is a rhombus. Find the value of x.

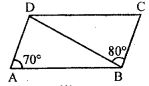
Answer :  (a) ABCD is a || gm

We have, AB || CD

∠ADB = ∠DBC (Alternate angles)

⇒ ∠ADB = 80° (Given, ∠DBC = 80°)

In ∆ADB, we have

∠A + ∠ADB + ∠ABD = 180° (Angle sum property of a triangle)

⇒ 70° + 80° + ∠ABD = 180°

⇒ 150^o + ∠ABD = 180^o

⇒ ∠ABD = 180^o – 150^o = 30^o

∠CDB = ∠ABD (Since, AB || CD and alternate angles)

∠CDB = 30^o

Hence, ∠ADB = 80^o and ∠CDB = 30^o.

(b) ∠BOC = 35^o and ∠CBO = 77^o

In ∆BOC,

∠BOC + ∠BCO + ∠CBO = 180^o (Angle sum property of a triangle)

⇒ ∠BOC = 180^o – 112^o = 68^o

Now, in || gm ABCD

We have,

∠AOD = ∠BOC

Hence, ∠AOD = 68^o.

(c) ABCD is a rhombus

So,  ∠A + ∠B = 180^o

(Sum of adjacent angles of a rhombus is 180^o)

⇒ 72^o + ∠B = 180^o (Given, ∠A = 72^o)

⇒ ∠B = 180^o – 72^o = 108^o

Therefore, x = ½ B

= ½ x 108^o

= 54^o

Question 5.  

(a) In figure (1) given below, ABCD is a parallelogram with perimeter 40. Find the values of x and y.

(b) In figure (2) given below. ABCD is a parallelogram. Find the values of x and y.

(c) In figure (3) given below. ABCD is a rhombus. Find x and y.

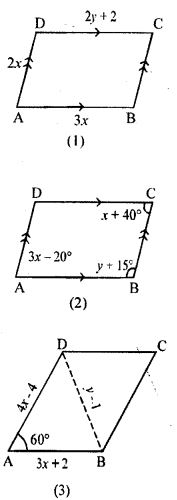
Answer :  (a) Since, ABCD is a parallelogram

So, AB = CD and BC = AD

⇒ 3x = 2y + 2

⇒ 3x – 2y = 2 …(i)

AB + BC + CD + DA = 40

⇒ 3x + 2x + 2y + 2 + 2x = 40

⇒ 7x + 2y = 40 – 2

⇒ 7x + 2y = 38 …(ii)

Now, adding (i) and (ii) we get

(3x – 2y) + (7x + 2y) = 2 + 38

⇒ 10x = 40

⇒ x = 40/10 = 4

3(4) – 2y = 2

⇒ 12 – 2y = 2

⇒ 2y = 12 – 2

⇒ y = 10/2 = 5

Therefore, x = 4 and y = 5

(b) In parallelogram ABCD, we have

∠A = ∠C (Opposite angles are same in || gm)

⇒ 3x – 20^o = x + 40^o

⇒ 3x – x = 40^o + 20^o

⇒ 2x = 60^o

⇒ x = 60^o/2 = 30^o …(i)

Also,

∠A + ∠B = 180^o (Sum of adjacent angles in || gm is equal to 180^o)

⇒ 3x – 20^o + y + 15^o = 180^o

⇒ 3x + y = 180^o + 20^o – 15^o

⇒ 3x + y = 185^o

⇒ 3(30^o) + y = 185^o

⇒ 90^o + y = 185^o

⇒ y = 185^o – 90^o = 95^o

Therefore,

x = 30^o and 95^o

(c) ABCD is a rhombus

So,

AB = CD

⇒ 3x + 2 = 4x – 4

⇒ 3x – 4x = -4 – 2

⇒ -x = -6

⇒ x = 6

Now, in ∆ABD we have

∠BAD = 60^o and AB = AD

∠ADB = ∠ABD

So,

∠ADB = (180^o – ∠BAD)/2

= (180^o – 60^o)/2

= 120^o/2 = 60^o

As ∆ABD is an equilateral triangle, all the angles of the triangle are 60^o

Therefore, AB = BD

3x + 2 = y – 1

⇒ 3(6) + 2 = y – 1

⇒ 18 + 2 = y – 1

⇒ 20 = y – 1

⇒ y = 20 + 1

⇒ y = 21

Thus,

x = 6 and y = 21.

Question 6. The diagonals AC and BD of a rectangle > ABCD intersect each other at P. If ∠ABD = 50°, find ∠DPC.

Answer : ABCD is a rectangle

AP = BP  (in rectangle diagonal are equal and bisect each other)

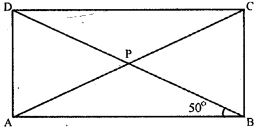
∠PAB = ∠PBA (Equal sides have equal opposite angles)

⇒ ∠PAB = 50^o (Since, given ∠PBA = 50^o)

Now, in ∆APB

∠APB + ∠ABP + ∠BAP = 180^o

⇒ ∠APB + 50^o + 50^o = 180^o

⇒ ∠APB = 180^o – 100^o

⇒ ∠APB = 80^o

Then,

∠DPB = ∠APB (Vertically opposite angles)

Therefore, ∠DPB = 80^o

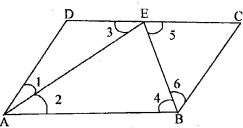
Question 7.  

(a) In figure (1) given below, equilateral triangle EBC surmounts square ABCD. Find angle BED represented by x.

(b) In figure (2) given below, ABCD is a rectangle and diagonals intersect at O. AC is produced to E. If ∠ECD = 146°, find the angles of the ∆ AOB.

(c) In figure (3) given below, ABCD is rhombus and diagonals intersect at O. If ∠OAB : ∠OBA = 3:2, find the angles of the ∆ AOD.

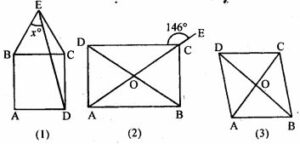
Answer :  EBC is an equilateral triangle, we have

EB = BC = EC …(i)

Also, ABCD is a square

So, AB = BC = CD = AD …(ii)

From (i) and (ii), we get

EB = EC = AB = BC = CD = AD …(iii)

in ∆ECD

∠ECD = ∠BCD + ∠ECB

= 90^o + 60^o

= 150^o …(iv)

EC = CD [From (iii)]

∠DEC = ∠CDE …(v)

∠ECD + ∠DEC + ∠CDE = 180^o

⇒ 150^o + ∠DEC + ∠DEC = 180^o [Using (iv) and (v)]

⇒ 2 ∠DEC = 180^o – 150^o = 30^o

⇒ ∠DEC = 30^o/2

⇒ ∠DEC = 15^o …(vi)

Now, ∠BEC = 60^o

⇒ ∠BED + ∠DEC = 60^o

⇒ x^o + 15^o = 60^o [From (vi)]

⇒ x = 60^o – 15^o

⇒ x = 45^o

Therefore, the value of x is 45^o.

(b) Given, ABCD is a rectangle

∠ECD = 146^o

As ACE is a straight line, we have

146^o + ∠ACD = 180^o [Linear pair]

⇒ ∠ACD = 180^o – 146^o = 34^o …(i)

And, ∠CAB = ∠ACD …(ii) [Alternate angles] 

From (i) and (ii), we have

∠CAB = 34^o

⇒ ∠OAB = 34^o …(iii)

In ∆AOB

AO = OB [Diagonals of a rectangle are equal and bisect each other]

∠OAB = ∠OBA …(iv) [Equal sides have equal angles opposite to them]

From (iii) and (iv),

∠OBA = 34^o …(v)

Now,

∠AOB + ∠OBA + ∠OAB = 180^o

⇒ ∠AOB + 34^o + 34^o = 180^o [Using (3) and (5)]

⇒ ∠AOB + 68^o = 180^o

⇒ ∠AOB = 180^o – 68^o = 112^o

∠AOB = 112^o, ∠OAB = 34^o and ∠OBA = 34^o

(c) Here, ABCD is a rhombus and diagonals intersect at O and ∠OAB : ∠OBA = 3 : 2

Let ∠OAB = 2x^o

Then,

∠OBA = 2x^o

∠OAB = 90^o

Now, in ∆AOB

∠OAB + ∠OBA = 180^o

⇒ 90^o + 3x^o + 2x^o = 180^o

⇒ 90^o + 5x^o = 180^o

⇒ 5x^o = 180^o – 90^o = 90^o

⇒ x^o = 90^o/5 = 18^o

∠OAB = 3x^o = 3 x 18^o = 54^o

⇒ OBA = 2x^o = 2×18^o = 36^o and ∠AOB = 90^o

Question 8.  

(a) In figure (1) given below, ABCD is a trapezium. Find the values of x and y.

(b) In figure (2) given below, ABCD is an isosceles trapezium. Find the values of x and.y.

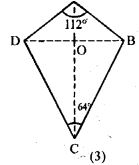
(c) In figure (3) given below, ABCD is a kite and diagonals intersect at O. If ∠DAB = 112° and ∠DCB = 64°, find ∠ODC and ∠OBA.

Answer :

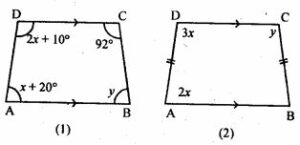
(a)  ABCD is a trapezium

∠A = x + 20^o, ∠B = y, ∠C = 92^o, ∠D = 2x + 10^o

∠B + ∠C = 180^o [Since AB || DC]

⇒ y + 92^o = 180^o

⇒ y = 180^o – 92^o = 88^o

∠A + ∠D = 180^o

⇒ x + 20^o + 2x + 10^o = 180^o

⇒ 3x + 30^o = 180^o

⇒ 3x = 180^o – 30^o = 150^o

⇒ x = 150^o/3 = 50^o

the value of x = 50^o and y = 88^o.

(b) ABCD is an isosceles trapezium BC = AD

∠A = 2x, ∠C = y and ∠D = 3x

ABCD is a trapezium and AB || DC

∠A + ∠D = 180^o

⇒ 2x + 3x = 180^o

⇒ 5x = 180^o

⇒ x = 180^o/5 = 36^o …(i)

AB = BC and AB || DC

So, ∠A + ∠C = 180^o

⇒ 2x + y = 180^o

⇒ 2×36^o + y = 180^o

⇒ 72^o + y = 180^o

⇒ y = 180^o – 72^o = 108^o

Therefore, value of x = 72^o and y = 108^o.

(c) ABCD is a kite and diagonal intersect at O.

∠DAB = 112^o and ∠DCB = 64^o

As AC is the diagonal of kite ABCD, we have

∠DCO = 64^o/2 = 32^o

∠DOC = 90^o [Diagonal of kites bisect at right angles]

In ∆OCD, we have

∠ODC = 180^o – (∠DCO + ∠DOC)

= 180^o – (32^o + 90^o)

= 180^o – 122^o

= 58^o

In ∆DAB, we have

∠OAB = 112^o/2 = 56^o

∠AOB = 90^o [Diagonal of kites bisect at right angles]

In ∆OAB,

∠OBA = 180^o – (∠OAB + ∠AOB)

= 180^o – (56^o + 90^o)

= 180^o – 146^o

= 34^o

Therefore, ∠ODC = 58^o and ∠OBA = 34^o.

Question 9.  

(i) Prove that each angle of a rectangle is 90°.
(ii) If the angle of a quadrilateral are equal, prove that it is a rectangle.
(iii) If the diagonals of a rhombus are equal, prove that it is a square.
(iv) Prove that every diagonal of a rhombus bisects the angles at the vertices.

Answer : (i)  ABCD is a rectangle

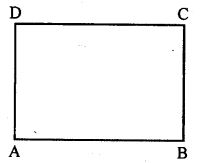
To prove: Each angle of rectangle = 90^o

Proof: 

In a rectangle opposite angles of a rectangle are equal

So, ∠A = ∠C and ∠B = ∠C

∠A + ∠B + ∠C + ∠D = 360^o [Sum of angles of a quadrilateral]

⇒ ∠A + ∠B + ∠A + ∠B = 360^o

⇒ 2(∠A + ∠B) = 360^o

⇒ (∠A + ∠B) = 360^o/2

⇒ ∠A + ∠B = 180^o

But, ∠A = ∠B [Angles of a rectangle]

∠A = ∠B = 90^o

∠A = ∠B = ∠C = ∠D = 90^o

Therefore, each angle of a rectangle is 90°.

(ii) In quadrilateral ABCD, we have

∠A = ∠B = ∠C = ∠D

To prove: ABCD is a rectangle

Proof:

∠A = ∠B = ∠C = ∠D

⇒ ∠A = ∠C and ∠B = ∠D

But these are opposite angles of the quadrilateral.

ABCD is a parallelogram

And, as ∠A = ∠B = ∠C = ∠D

Hence, ABCD is a rectangle.

(iii) ABCD is a rhombus in which AC = BD

To prove: ABCD is a square

Proof:  Join AC and BD.

Now, in ∆ABC and ∆DCB we have

∠AB = ∠DC [Sides of a rhombus]

∠BC = ∠BC [Common]

∠AC = ∠BD [Given]

∆ABC ≅ ∆DCB by S.S.S axiom of congruency

∠ABC = ∠DBC [By C.P.C.T]

But these are made by transversal BC on the same side of parallel lines AB and CD.

So, ∠ABC + ∠DBC = 180^o

∠ABC = 90^o

Therefore, ABCD is a square.

(iv) ABCD is rhombus.

To prove: Diagonals AC and BD bisects ∠A, ∠C, ∠B and ∠D respectively

Proof:

In ∆AOD and ∆COD, we have

AD = CD [sides of a rhombus are all equal]

OD = OD [Common]

AO = OC [Diagonal of rhombus bisect each other]

So, ∆AOD ≅ ∆COD by S.S.S axiom of congruency

Thus,

∠AOD = ∠COD [By C.P.C.T]

So, ∠AOD + ∠COD = 180^o [Linear pair]

∠AOD = 180^o

∠AOD = 90^o

And, ∠COD = 90^o

OD ⊥ AC ⇒ BD ⊥ AC

Also, ∠ADO = ∠CDO [By C.P.C.T]

OD bisect ∠D

BD bisect ∠D

we can prove that BD bisect ∠B and AC bisect the ∠A and ∠C.

Question 10.  ABCD is a parallelogram. If the diagonal AC bisects ∠A, then prove that:

(i) AC bisects ∠C
(ii) ABCD is a rhombus
(iii) AC ⊥ BD.

Answer :  In parallelogram ABCD in which diagonal AC bisects ∠A

To prove: (i) AC bisects ∠C

(ii) ABCD is a rhombus

(iii) AC ⊥ BD

Proof:

(i) As AB || CD, we have [Opposite sides of a || gm]

∠DCA = ∠CAB

Similarly,

∠DAC = ∠DCB

But, ∠CAB = ∠DAC [Since, AC bisects ∠A]

Therefore,

∠DCA = ∠ACB and AC bisects ∠C.

(ii) As AC bisects ∠A and ∠C

And, ∠A = ∠C

ABCD is a rhombus.

(iii) Since, AC and BD are the diagonals of a rhombus and

AC and BD bisect each other at right angles

Therefore, AC ⊥ BD

Question 11.  

(i) Prove that bisectors of any two adjacent angles of a parallelogram are at right angles.

(ii) Prove that bisectors of any two opposite angles of a parallelogram are parallel.

(iii) If the diagonals of a quadrilateral are equal and bisect each other at right angles, then prove that it is a square.

Answer :  (i) Given AM bisect angle A and BM bisects angle of || gm ABCD.

To prove: ∠AMB = 90^o

Proof:  We have,

∠A + ∠B = 180^o [AD || BC and AB is the transversal]

⇒ ½ (∠A + ∠B) = 180^o/2

⇒ ½ ∠A + ½ ∠B = 90^o

⇒ ∠MAB + ∠MBA = 90^o [Since, AM bisects ∠A and BM bisects ∠B]

in ∆AMB

∠AMB + ∠MAB + ∠MBA = 180^o [Angles sum property of a triangle]

⇒ ∠AMB + 90^o = 180^o

⇒ ∠AMB = 180^o – 90^o = 90^o

Therefore, bisectors of any two adjacent angles of a parallelogram are at right angles.

(ii) A || gm ABCD in which bisector AR of ∠A meets DC in R and bisector CQ of ∠C meets AB in Q

∠A = ∠C [Opposite angles of || gm are equal]

½ ∠A = ½ ∠C

∠DAR = ∠BCQ [Since, AR is bisector of ½ ∠A and CQ is the bisector of ½ ∠C]

Now, in ∆ADR and ∆CBQ

∠DAR = ∠BCQ [Proved above]

AD = BC [Opposite sides of || gm ABCD are equal]

So, ∆ADR ≅ ∆CBQ, by A.S.A axiom of congruency

Then by C.P.C.T, we have

∠DRA = ∠BCQ

∠DRA = ∠RAQ [Alternate angles since, DC || AB]

∠RAQ = ∠BCQ

But these are corresponding angles,

Hence, AR || CQ.

(iii) In quadrilateral ABCD, diagonals AC and BD are equal and bisect each other at right angles

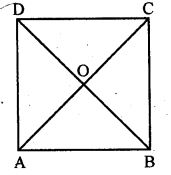
To prove: ABCD is a square

Proof:  In ∆AOB and ∆COD, we have

AO = OC [Given]

BO = OD [Given]

∠AOB = ∠COD [Vertically opposite angles]

So, ∆AOB ≅ ∆COD, by S.A.S axiom of congruency

By C.P.C.T, we have

AB = CD

and ∠OAB = ∠OCD

AB || CD

ABCD is a parallelogram

In a parallelogram, the diagonal bisect each other and are equal

Therefore, ABCD is a square.

Question 12.

(i) If ABCD is a rectangle in which the diagonal BD bisect ∠B, then show that ABCD is a square.
(ii) Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Answer :   (i) ABCD is a rectangle and its diagonals AC bisects ∠A and ∠C

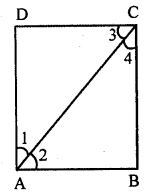
To prove: ABCD is a square

Proof:  As AC bisects ∠A and ∠C

So, ∠1 = ∠2 and ∠3 = ∠4

But, ∠A = ∠C = 90^o

∠2 = 45^o and ∠4 = 45^o

And, AB = BC [Opposite sides of equal angles]

AB = CD and BC = AD

So, AB = BC = CD = DA

Hence, ABCD is a square.

(ii) In quadrilateral ABCD diagonals AC and BD are equal and bisect each other at right angle

To prove: ABCD is a square

Proof:  In ∆AOB and ∆BOC, we have

AO = CO

OB = OB

∠AOB = ∠COB [Each 90^o]

So, ∆AOB ≅ ∆BOC, by S.A.S axiom

By C.P.C.T, we have

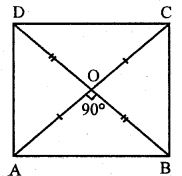
AB = BC …(i)

Similarly, in ∆BOC and ∆COD

OB = OD

OC = OC

∠BOC = ∠COD [Each 90^o]

So, ∆BOC ≅ ∆COD, by S.A.S axiom

By C.P.C.T, we have

BC = CD …(ii)

From (i) and (ii), we have

AB = BC = CD = DA

Therefore, ABCD is a square.

Question 13. P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.

Answer :  ABCD is a parallelogram, P and Q are the points on AB and DC. Diagonals AC and BD intersect each other at O.

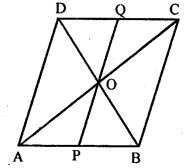
To prove:   Diagonals of || gm ABCD bisect each other at O

So, AO = OC and BO = OD

Now, in ∆AOP and ∆COQ we have

AO = OC and BO = OD

Now, in ∆AOP and ∆COQ

AO = OC

∠OAP = ∠OCQ

∠AOP = ∠COQ

So, ∆AOP ≅ ∆COQ by S.A.S axiom

Thus, by C.P.C.T

OP = OQ

Therefore, O bisects PQ.

Question 14. 

(a) In figure (1) given below, ABCD is a parallelogram and X is mid-point of BC. The line AX produced meets DC produced at Q. The parallelogram ABPQ is completed. Prove that:
(i) the triangles ABX and QCX are congruent;
(ii)DC = CQ = QP

(b) In figure (2) given below, points P and Q have been taken on opposite sides AB and CD respectively of a parallelogram ABCD such that AP = CQ. Show that AC and PQ bisect each other.

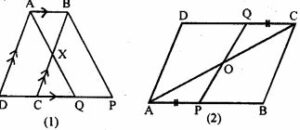
Answer  :  (a) ABCD is parallelogram and X is mid-point of BC. The line AX produced meets DC produced at Q and ABPQ is a || gm.

To prove:  (i) ∆ABX ≅ ∆QCX,  (ii) DC = CQ = QP

Proof:  In ∆ABX and ∆QCX, we have

BX = XC

∠AXB = ∠CXQ

∠XCQ = ∠XBA

So, ABX ≅ ∆QCX by A.S.A axiom of congruence

Now, by C.P.C.T

CQ = AB

But,   AB = DC and AB = QP [As ABCD and ABPQ are ||gms]

Hence,  DC = CQ = QP

(b) In || gm ABCD, P and Q are points on AB and CD respectively, PQ and AC intersect each other at O and AP = CQ

To prove: AC and PQ bisect each other i.e. AO = OC and PO = OQ

Proof:  In ∆AOP and ∆COQ

AP = CQ [Given]

∠AOP = ∠COQ

∠OAP = ∠OCP

So, ∆AOP ≅ ∆COQ by A.A.S axiom of congruence

Now, by C.P.C.T

OP = OQ and OA = OC

Hence proved.

Question 15. ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP=DQ, prove that AP and DQ are perpendicular to each other.

Answer : ABCD is a square. P is any point on BC and Q is any point on AB and these points are taken such that AP = DQ

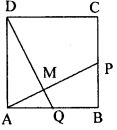
To prove: AP ⊥ DQ

Proof:  In ∆ABP and ∆ADQ, we have

AP = DQ [Given]

AD = AB [Sides of square ABCD]

∠DAQ = ∠ABP [Each 90^o]

So, ∆ABP ≅ ∆ADQ by R.H.S axiom of congruency

by C.P.C.T

∠BAP = ∠ADQ

But, ∠BAD = 90^o

∠BAD = ∠BAP + ∠PAD …(i)

⇒ 90^o = ∠BAP + ∠PAD

⇒ ∠BAP + ∠PAD = 90^o

⇒ ∠BAP + ∠ADQ = 90^o

Now, in ∆ADM we have

(∠MAD + ∠ADM) + ∠AMD = 180^o

⇒ 90^o + ∠AMD = 180^o [From (i)]

⇒ ∠AMD = 180^o – 90^o = 90^o

So, DM ⊥ AP

⇒ DQ ⊥ AP

Therefore, AP ⊥ DQ

Question 16. If P and Q are points of trisection of the diagonal BD of a parallelogram ABCD, prove that CQ || AP.

Answer :  ABCD is a || gm is which BP = PQ = QD

To prove: CQ || AP

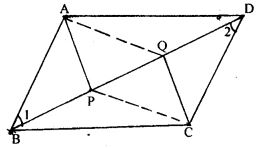
Proof:

In || gm ABCD, we have

AB = CD [Opposite sides of a || gm are equal]

And BD is the transversal

So, ∠1 = ∠2 …(i) [Alternate interior angles] 

Now, in ∆ABP and ∆DCQ

AB = CD [Opposite sides of a || gm are equal]

∠1 = ∠2 [From (i)]

BP = QD [Given]

So, ∆ABP ≅ ∆DCQ by S.A.S axiom of congruency

Then by C.P.C.T, we have

AP = QC

Also, ∠APB = ∠DQC [By C.P.C.T]

-∠APB = -∠DQC [Multiplying both sides by -1]

⇒ 180^o – ∠APB = 180^o – ∠DQC

⇒ ∠APQ = ∠CQP

Therefore, AP || QC

⇒ CQ || AP.

Question 17. A transversal cuts two parallel lines at A and B. The two interior angles at A are bisected and so are the two interior angles at B ; the four bisectors form a quadrilateral ABCD. Prove that

(i) ABCD is a rectangle.
(ii) CD is parallel to the original parallel lines.

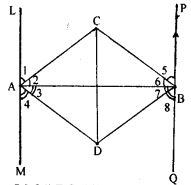
Answer :  LM || PQ and AB is the transversal line cutting ∠M at A and PQ at B

AC, AD, BC and BD is the bisector of ∠LAB, ∠BAM, ∠PAB and ∠ABQ respectively.

AC and BC intersect at C and AD and BD intersect at D.

A quadrilateral ABCD is formed.

To prove: (i) ABCD is a rectangle

(ii) CD || LM and PQ

Proof:  (1) ∠LAB + ∠BAM = 180^o

⇒ ½ (∠LAB + ∠BAM) = 90^o

⇒ ½ ∠LAB + ½ ∠BAM = 90^o

⇒ ∠2 + ∠3 = 90^o [AC and AD is bisector of ∠LAB & ∠BAM respectively]

⇒ ∠CAD = 90^o

⇒ ∠A = 90^o

(2) Similarly, ∠PBA + ∠QBA = 180^o

⇒ ½ (∠PBA + ∠QBA) = 90^o

⇒ ½ ∠PBA + ½ ∠QBA = 90^o

⇒ ∠6 + ∠7 = 90^o [ BC and BD is bisector of ∠PAB & ∠QBA respectively]

⇒ ∠CBD = 90^o

⇒ ∠B = 90^o

(3) ∠LAB + ∠ABP = 180^o [Sum of co-interior angles is 180^o and given LM || PQ]

⇒ ½ ∠LAB + ½ ∠ABP = 90^o

⇒ ∠2 + ∠6 = 90^o [Since, AC and BC is bisector of ∠LAB & ∠PBA respectively]

(4) In ∆ACB,

∠2 + ∠6 + ∠C = 180^o 

⇒ (∠2 + ∠6) + ∠C = 180^o

⇒ 90^o + ∠C = 180^o [using (3)]

⇒ ∠C = 180^o – 90^o

⇒ ∠C = 90^o

(5) ∠MAB + ∠ABQ = 180^o [Sum of co-interior angles is 180^o and given LM || PQ]

⇒ ½ ∠MAB + ½ ∠ABQ = 90^o

⇒ ∠3 + ∠7 = 90^o [Since, AD and BD is bisector of ∠MAB & ∠ABQ respectively]

(6) In ∆ADB,

∠3 + ∠7 + ∠D = 180^o [Angles sum property of a triangle]

⇒ (∠3 + ∠7) + ∠D = 180^o

⇒ 90^o + ∠D = 180^o [using (5)]

⇒ ∠D = 180^o – 90^o

⇒ ∠D = 90^o

(7) ∠LAB + ∠BAM = 180^o

∠BAM = ∠ABP [From (1) and (2)]

⇒ ½ ∠BAM = ½ ∠ABP

⇒ ∠3 = ∠6 [Since, AD and BC is bisector of ∠BAM and ∠ABP respectively]

∠2 = ∠7

(8) In ∆ABC and ∆ABD,

∠2 = ∠7 [From (7)]

AB = AB [Common]

∠6 = ∠3 [From (7)]

∆ABC ≅ ∆ABD by A.S.A axiom of congruency

by C.P.C.T we have

AC = DB

CB = AD

(9) ∠A = ∠B = ∠C =∠D = 90^o [From (1), (2), (3) and (4)]

AC = DB [Proved in (8)]

CB = AD [Proved in (8)]

Hence, ABCD is a rectangle.

(10) ABCD is a rectangle [From (9)]

OA = OD [Diagonals of rectangle bisect each other]

(11) In ∆AOD, we have

OA = OD [From (10)]

∠9 = ∠3

(12) ∠3 = ∠4 [AD bisects ∠MAB]

(13) ∠9 = ∠4 [From (11) and (12)]

But these are alternate angles.

OD || LM

⇒ CD || LM

∠10 = ∠8

But these are alternate angles,

So, OD || PQ

⇒ CD || PQ

(14) CD || LM [Proved in (13)]

CD || PQ [Proved in (13)]

Question 18. In a parallelogram ABCD, the bisector of ∠A meets DC in E and AB = 2 AD. Prove that

(i) BE bisects ∠B
(ii) ∠AEB = a right angle.

Answer :   (1) In || gm ABCD

∠1 = ∠2 [AD bisects angles ∠A]

(2) AB || DC and AE is the transversal

∠2 = ∠3 [Alternate angles]

(3) ∠1 = ∠2 [From (1) and (2)]

(4) In ∆ADE, we have

∠1 = ∠3 [Proved in (3)]

DE = AD

⇒ AD = DE

(5) AB = 2 AD [Given]

AB/2 = AD

AB/2 = DE [using (4)]

DC/2 = DE [AB = DC, opposite sides of a || gm are equal]

So, E is the mid-point of D.

⇒ DE = EC

(6) AD = BC [Opposite sides of a || gm are equal]

(7) DE = BC [From (4) and (6)]

(8) EC = BC [From (5) and (7)]

(9) In ∆BCE, we have

EC = BC [Proved in (8)]

∠6 = ∠5

(10) AB || DC and BE is the transferal

∠4 = ∠5 [Alternate angles]

(11) ∠4 = ∠6 [From (9) and (10)]

So, BE is bisector of ∠B

(12) ∠A + ∠B = 180^o [Sum of co-interior angles is equal to 180^o, AD || BC]

⇒ ½ ∠A + ½ ∠B = 180^o/2

⇒ ∠2 + ∠4 = 90^o [AE is bisector of ∠A and BE is bisector of ∠B]

(13) In ∆APB,

∠AEB + ∠2 + ∠4 = 180^o

⇒ ∠AEB + 90^o = 180^o

Therefore, ∠AEB = 90^o

Question 19. ABCD is a parallelogram, bisectors of angles A and B meet at E which lie on DC. Prove that AB

Answer :  ABCD is a parallelogram in which bisector of ∠A and ∠B meets DC in E

To prove: AB = 2 AD

Proof:   In parallelogram ABCD, we have AB || DC

∠1 = ∠5 [Alternate angles, AE is transversal]

∠1 = ∠2 [AE is bisector of ∠A, given]

Thus,  ∠2 = ∠5 …(i)

Now, in ∆AED

DE = AD [Sides opposite to equal angles are equal]

∠3 = ∠6 [Alternate angles]

∠3 = ∠4 [Since, BE is bisector of ∠B (given)]

∠4 = ∠6 …(ii)

In ∆BCE, we have

BC = EC [Sides opposite to equal angles are equal]

AD = BC [Opposite sides of || gm are equal]

AD = DE = EC [From (i) and (ii)]

AB = DC [Opposite sides of a || gm are equal]

AB = DE + EC

= AD + AD

AB = 2 AD

Question 20. ABCD is a square and the diagonals intersect at O. If P is a point on AB such that AO =AP, prove that 3 ∠POB = ∠AOP.

Answer :  ABCD is a square and the diagonals intersect at O. P is the point on AB such that AO = AP

To prove: 3 ∠POB = ∠AOP

Proof:  (1) In square ABCD, AC is a diagonal

∠CAB = 45^o

∠OAP = 45^o

(2) In ∆AOP,

∠OAP = 45^o [From (1)]

AO = AP [Sides opposite to equal angles are equal]

Now,

∠AOP + ∠APO + ∠OAP = 180^o

⇒ ∠AOP + ∠AOP + 45^o = 180^o

⇒ 2∠AOP = 180^o – 45^o

⇒ ∠AOP = 135^o/2

(3) ∠AOB = 90^o [Diagonals of a square bisect at right angles]

∠AOP + ∠POB = 90^o

⇒ 135^o/2 + ∠POB = 90^o [From (2)]

⇒ ∠POB = 90^o – 135^o/2

= (180^o – 135^o)/2

= 45^o/2

3∠POB = 135^o/2 [Multiplying both sides by 3]

Therefore,

∠AOP = 3 ∠POB [From (2) and (3)]

Question 21. ABCD is a square. E, F, G and H are points on the sides AB, BC, CD and DA respectively such that AE = BF = CG = DH. Prove that EFGH is a square.

Answer :

ABCD is a square in which E, F, G and H are points on AB, BC, CD and DA

Such that AE = BF = CG = DH

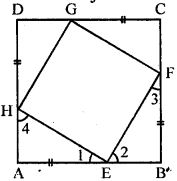
EF, FG, GH and HE are joined

To prove: EFGH is a square

Proof:  Since, AE = BF = CG = DH

EB = FC = GD = HA

In ∆AEH and ∆BFE

AE = BF [Given]

AH = EB [Proved]

∠A = ∠B [Each 90^o]

∆AEH ≅ ∆BFE by S.A.S axiom of congruency

by C.P.C.T we have

EH = EF

And ∠4 = ∠2

But ∠1 + ∠4 = 90^o

⇒ ∠1 + ∠2 = 90^o

Thus, ∠HEF = 90^o

Therefore, EFGH is a square.

Question 22.  (a) In the Figure (1) given below, ABCD and ABEF are parallelograms. Prove that

(i) CDFE is a parallelogram
(ii) FD = EC
(iii) Δ AFD = ΔBEC.

(b) In the figure (2) given below, ABCD is a parallelogram, ADEF and AGHB are two squares. Prove that FG = AC

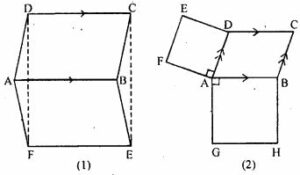
Answer :  To prove: 

(i) CDFE is a parallelogram

(ii) FD = EC

(iii) Δ AFD = ΔBEC

Proof:  

(1) DC || AB and DC = AB [ABCD is a || gm]

(2) FE || AB and FE = AB [ABEF is a || gm]

(3) DC || FE and DC = FE [From (1) and (2)]

Thus, CDFE is a || gm

(4) CDEF is a || gm

So, FD = EC

(5) In ∆AFD and ∆BEC, we have

AD = BC [Opposite sides of || gm ABCD are equal]

AF = BE [Opposite sides of || gm ABEF are equal]

FD = BE [From (4)]

Hence, ∆AFD ≅ ∆BEC by S.S.S axiom of congruency

(b) ABCD is a || gm, ADEF and AGHB are two squares

To prove: FG = AC

Proof:  (1) ∠FAG + 90^o + 90^o + ∠BAD = 360^o [At a point total angle is 360^o]

⇒ ∠FAG = 360^o – 90^o – 90^o – ∠BAD

⇒ ∠FAG = 180^o – ∠BAD

(2) ∠B + ∠BAD = 180^o [Adjacent angle in || gm is equal to 180^o]

⇒ ∠B = 180^o – ∠BAD

(3) ∠FAG = ∠B [From (1) and (2)]

(4) In ∆AFG and ∆ABC, we have

AF = BC [FADE and ABCD both are squares on the same base]

AG = AB

∠FAG = ∠B [From (3)]

∆AFG ≅ ∆ABC by S.A.S axiom of congruency

Therefore, by C.P.C.T

FG = AC

Question 23. ABCD is a rhombus in which ∠A = 60°. Find the ratio AC : BD.

Answer : Let each side of the rhombus ABCD be a

∠A = 60^o

ABD is an equilateral triangle

⇒ BD = AB = a

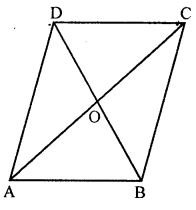
We know that, the diagonals of a rhombus bisect each other at right angles

So, in right triangle AOB, we have

AO² = AB² – OB²

= a² – (½ a)²

= a² – a²/4

= 3a²/4

AO = √(3a²/4) = √3a/2

But, AC = 2 AO = 2 x 3a/2 = 3a

Therefore,

AC : BD = √3a : a = √3 : 1

—  : End of ML Aggarwal Rectilinear Figures Exe-13.1 Class 9 ICSE Maths Solutions :–

Return to :-  ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends