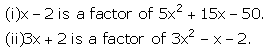Remainder And Factor Theorems Concise Maths Solution Chapter-8 for ICSE Board Class 10th Concise Solution Remainder And Factor Theorems Concise Maths Solution Chapter-8 for ICSE Maths Class 10 is available here. All Solution of Concise of Chapter 8 Remainder And Factor Theorems has been solved according instruction given by council. This is the Solution of Chapter-8 Remainder And Factor Theorems for ICSE Class 10th .ICSE Maths text book of Concise is In series of famous ICSE writer in maths. Concise is most famous among students. With the help of Concise Solution student can achieve their goal in 2020 exam of council.
Remainder And Factor Theorems Concise Maths Solution Chapter-8
The Solution of Concise Mathematics Chapter8 Remainder And Factor Theorems for ICSE Class 10 have been solved by experience teachers from across the globe to help students of class 10th ICSE board exams conducted by the ICSE (Indian Council of Secondary Education) board papering in 2020. Therefore the ICSE Class 10th Maths Solution of Concise solve problems of exercise related to various topics which are prescribed in most ICSE Maths textbooks.
Chapter-8 Remainder And Factor Theorems Concise Maths Solution for ICSE Board Class 10th— Select Topics
Exe – 8 (A) , Exe -8 (B) , Exe – 8 (C) ,
How to Solve Concise Maths Selina Publications Chapter-8 Remainder And Factor Theorems
Note :- Before viewing Solutions of Chapter -8Remainder And Factor Theorems of Concise Maths read the Chapter Carefully then solve all example of your text book. The Chapter- 8 Remainder And Factor Theorems is main Chapter in ICSE board
Exercise – 8(A), Remainder And Factor Theorems Concise Maths Solution
Question 1
Find, in each case, the remainder when:
Answer 1
By remainder theorem we know that when a polynomial f (x) is divided by x – a, then the remainder is f(a).

Question 2
Show that:
Answer 2
(x – a) is a factor of a polynomial f(x) if the remainder, when f(x) is divided by (x – a), is 0, i.e., if f(a) = 0.
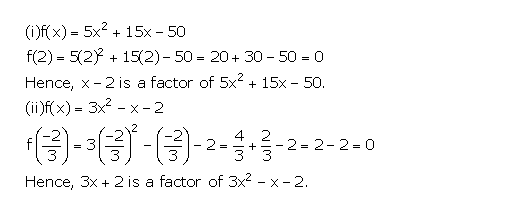
Question 3
Use the Remainder Theorem to find which of the following is a factor of 2x3 + 3x2 – 5x – 6.
(i) x + 1
(ii) 2x – 1
(iii) x + 2
Answer 3
By remainder theorem we know that when a polynomial f (x) is divided by x – a, then the remainder is f(a).
Let f(x) = 2x3 + 3x2 – 5x – 6
(i) f (-1) = 2(-1)3 + 3(-1)2 – 5(-1) – 6 = -2 + 3 + 5 – 6 = 0
Thus, (x + 1) is a factor of the polynomial f(x).
(ii)

Thus, (2x – 1) is not a factor of the polynomial f(x).
(iii) f (-2) = 2(-2)3 + 3(-2)2 – 5(-2) – 6 = -16 + 12 + 10 – 6 = 0
Thus, (x + 2) is a factor of the polynomial f(x).
Question 4
(i) If 2x + 1 is a factor of 2x2 + ax – 3, find the value of a.
(ii) Find the value of k, if 3x – 4 is a factor of expression 3x2 + 2x – k.
Answer 4
(i) 2x + 1 is a factor of f(x) = 2x2 + ax – 3.
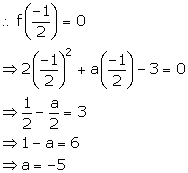
(ii) 3x – 4 is a factor of g(x) = 3x2 + 2x – k.

Question 5
Find the values of constants a and b when x – 2 and x + 3 both are the factors of expression x3 + ax2 + bx – 12.
Answer 5
Let f(x) = x3 + ax2 + bx – 12
x – 2 = 0 x = 2
x – 2 is a factor of f(x). So, remainder = 0
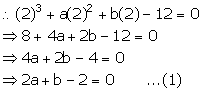
x + 3 = 0 x = -3
x + 3 is a factor of f(x). So, remainder = 0
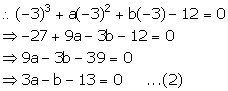
Adding (1) and (2), we get,
5a – 15 = 0
a = 3
Putting the value of a in (1), we get,
6 + b – 2 = 0
b = -4
Question 6
find the value of k, if 2x + 1 is a factor of (3k + 2)x3 + (k – 1).
Answer 6
Let f(x) = (3k + 2)x3 + (k – 1)
2x + 1 = 0 ![]()
![]()
Since, 2x + 1 is a factor of f(x), remainder is 0.
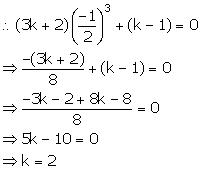
Question 7
Find the value of a, if x – 2 is a factor of 2x5 – 6x4 – 2ax3 + 6ax2 + 4ax + 8.
Answer 7
f(x) = 2x5 – 6x4 – 2ax3 + 6ax2 + 4ax + 8
x – 2 = 0 x = 2
Since, x – 2 is a factor of f(x), remainder = 0.
2(2)5 – 6(2)4 – 2a(2)3 + 6a(2)2 + 4a(2) + 8 = 0
64 – 96 – 16a + 24a + 8a + 8 = 0
-24 + 16a = 0
16a = 24
a = 1.5
Question 8
Find the values of m and n so that x – 1 and x + 2 both are factors of x3 + (3m + 1) x2 + nx – 18.
Answer 8
Let f(x) = x3 + (3m + 1) x2 + nx – 18
x – 1 = 0 x = 1
x – 1 is a factor of f(x). So, remainder = 0
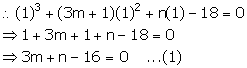
x + 2 = 0 ⇒ x = -2
x + 2 is a factor of f(x). So, remainder = 0
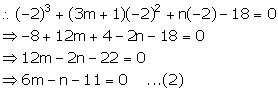
Adding (1) and (2), we get,
9m – 27 = 0
m = 3
Putting the value of m in (1), we get,
3(3) + n – 16 =0
9 + n – 16 = 0
n = 7
Question 9
When x3 + 2x2 – kx + 4 is divided by x – 2, the remainder is k. Find the value of constant k.
Answer 9
Let f(x) = x3 + 2x2 – kx + 4
x – 2 = 0 x = 2
On dividing f(x) by x – 2, it leaves a remainder k.
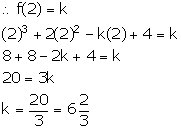
Question 10
Find the value of a, if the division of ax3 + 9x2 + 4x – 10 by x + 3 leaves a remainder 5.
Answer 10
Let f(x) = ax3 + 9x2 + 4x – 10
x + 3 = 0 x = -3
On dividing f(x) by x + 3, it leaves a remainder 5.

Question 11
If x3 + ax2 + bx + 6 has x – 2 as a factor and leaves a remainder 3 when divided by x – 3, find the values of a and b.
Answer 11
Let f(x) = x3 + ax2 + bx + 6
x – 2 = 0 ⇒ x = 2
Since, x – 2 is a factor, remainder = 0

x – 3 = 0 ⇒ x = 3
On dividing f(x) by x – 3, it leaves a remainder 3.
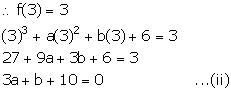
Subtracting (i) from (ii), we get,
a + 3 = 0
a = -3
Substituting the value of a in (i), we get,
-6 + b + 7 = 0
b = -1
Question 12
The expression 2x3 + ax2 + bx – 2 leaves remainder 7 and 0 when divided by 2x – 3 and x + 2 respectively. Calculate the values of a and b.
Answer 12
Let f(x) = 2x3 + ax2 + bx – 2
2x – 3 = 0 ![]() x =
x = ![]()
On dividing f(x) by 2x – 3, it leaves a remainder 7.

x + 2 = 0 x = -2
On dividing f(x) by x + 2, it leaves a remainder 0.
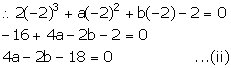
Adding (i) and (ii), we get,
7a – 21 = 0
a = 3
Substituting the value of a in (i), we get,
![]()
9 + 2b – 3 = 0
2b = -6
b = -3
Question 13
What number should be added to 3x3 – 5x2 + 6x so that when resulting polynomial is divided by x – 3, the remainder is 8?
Answer 13
Let the number k be added and the resulting polynomial be f(x).
So, f(x) = 3x3 – 5x2 + 6x + k
It is given that when f(x) is divided by (x – 3), the remainder is 8.

Thus, the required number is -46.
Question 14
What number should be subtracted from x3 + 3x2 – 8x + 14 so that on dividing it with x – 2, the remainder is 10.
Answer 14
Let the number to be subtracted be k and the resulting polynomial be f(x).
So, f(x) = x3 + 3x2 – 8x + 14 – k
It is given that when f(x) is divided by (x – 2), the remainder is 10.
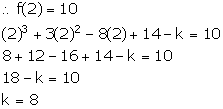
Thus, the required number is 8.
Question 15
The polynomials 2x3 – 7x2 + ax – 6 and x3 – 8x2 + (2a + 1)x – 16 leaves the same remainder when divided by x – 2. Find the value of ‘a’.
Answer 15
Let f(x) = 2x3 – 7x2 + ax – 6
x – 2 = 0 x = 2
When f(x) is divided by (x – 2), remainder = f(2)
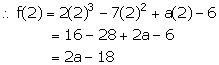
Let g(x) = x3 – 8x2 + (2a + 1)x – 16
When g(x) is divided by (x – 2), remainder = g(2)
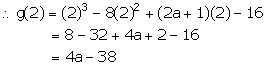
By the given condition, we have:
f(2) = g(2)
2a – 18 = 4a – 38
4a – 2a = 38 – 18
2a = 20
a = 10
Thus, the value of a is 10.
Question 16
If (x – 2) is a factor of the expression 2x3 + ax2 + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b
Answer 16

Question 17
Find ‘a’ if the two polynomials ax3 + 3x2 – 9 and 2x3 + 4x + a, leave the same remainder when divided by x + 3.
Answer 17

Concise Maths Solution Exercise – 8(B) Remainder And Factor Theorems
Question 1
Using the Factor Theorem, show that:
(i) (x – 2) is a factor of x3 – 2x2 – 9x + 18. Hence, factorise the expression x3 – 2x2 – 9x + 18 completely.
(ii) (x + 5) is a factor of 2x3 + 5x2 – 28x – 15. Hence, factorise the expression 2x3 + 5x2 – 28x – 15 completely.
(iii) (3x + 2) is a factor of 3x3 + 2x2 – 3x – 2. Hence, factorise the expression 3x3 + 2x2 – 3x – 2 completely.
Answer 1
(i) Let f(x) = x3 – 2x2 – 9x + 18
x – 2 = 0 ⇒x = 2
Remainder = f(2)
= (2)3 – 2(2)2 – 9(2) + 18
= 8 – 8 – 18 + 18
= 0
Hence, (x – 2) is a factor of f(x).
Now, we have:
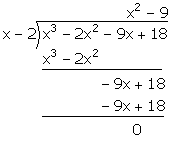
x3 – 2x2 – 9x + 18 = (x – 2) (x2 – 9) = (x – 2) (x + 3) (x – 3)
(ii) Let f(x) = 2x3 + 5x2 – 28x – 15
x + 5 = 0 ⇒ x = -5
Remainder = f(-5)
= 2(-5)3 + 5(-5)2 – 28(-5) – 15
and = -250 + 125 + 140 – 15
so = -265 + 265
Therefore = 0
Hence, (x + 5) is a factor of f(x).
Now, we have:
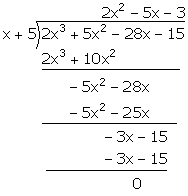
2x3 + 5x2 – 28x – 15 = (x + 5) (2x2 – 5x – 3)
= (x + 5) [2x2 – 6x + x – 3]
and = (x + 5) [2x(x – 3) + 1(x – 3)]
then = (x + 5) (2x + 1) (x – 3)
(iii) Let f(x) = 3x3 + 2x2 – 3x – 2
3x + 2 = 0 ![]()

Hence, (3x + 2) is a factor of f(x).
Now, we have:
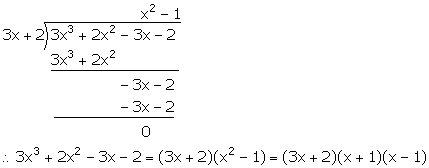
Question 2
Using the Remainder Theorem, factorise each of the following completely.
(i) 3x3 + 2x2 − 19x + 6
(ii) 2x3 + x2 – 13x + 6
(iii) 3x3 + 2x2 – 23x – 30
(iv) 4x3 + 7x2 – 36x – 63
(v) x3 + x2 – 4x – 4
Answer 2
(i)
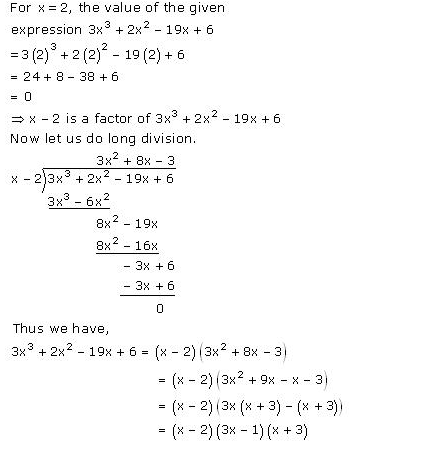
(ii) Let f(x) = 2x3 + x2 – 13x + 6
For x = 2,
f(x) = f(2) = 2(2)3 + (2)2 – 13(2) + 6 = 16 + 4 – 26 + 6 = 0
Hence, (x – 2) is a factor of f(x).
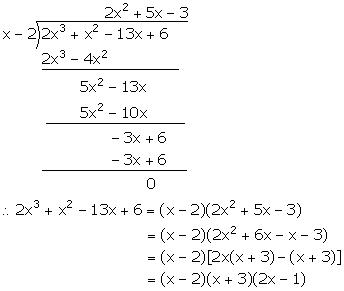
(iii) f(x) = 3x3 + 2x2 – 23x – 30
For x = -2,
f(x) = f(-2) = 3(-2)3 + 2(-2)2 – 23(-2) – 30
= -24 + 8 + 46 – 30 = -54 + 54 = 0
Hence, (x + 2) is a factor of f(x).
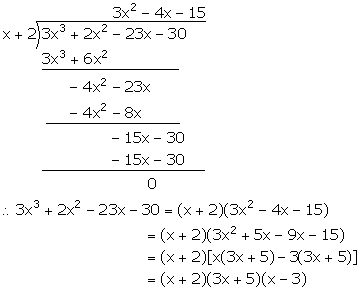
(iv) f(x) = 4x3 + 7x2 – 36x – 63
For x = 3,
f(x) = f(3) = 4(3)3 + 7(3)2 – 36(3) – 63
= 108 + 63 – 108 – 63 = 0
Hence, (x + 3) is a factor of f(x).
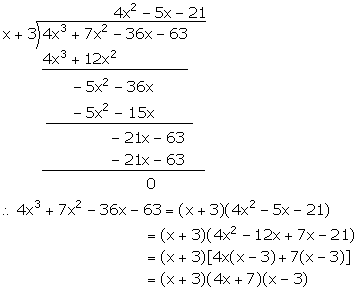
(v) f(x) = x3 + x2 – 4x – 4
For x = -1,
f(x) = f(-1) = (-1)3 + (-1)2 – 4(-1) – 4
= -1 + 1 + 4 – 4 = 0
Hence, (x + 1) is a factor of f(x).
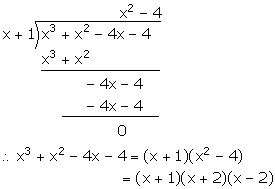
Question 3
Using the Remainder Theorem, factorise the expression 3x3 + 10x2 + x – 6. Hence, solve the equation 3x3 + 10x2 + x – 6 = 0.
Answer 3
Let f(x) = 3x3 + 10x2 + x – 6
For x = -1,
f(x) = f(-1) = 3(-1)3 + 10(-1)2 + (-1) – 6 = -3 + 10 – 1 – 6 = 0
Hence, (x + 1) is a factor of f(x).
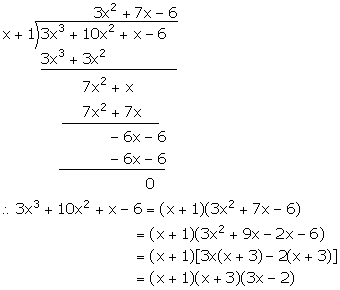
Now, 3x3 + 10x2 + x – 6 = 0
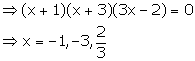
Question 4
Factorise the expression f (x) = 2x3 – 7x2 – 3x + 18. Hence, find all possible values of x for which f(x) = 0.
Answer 4
f (x) = 2x3 – 7x2 – 3x + 18
For x = 2,
f(x) = f(2) = 2(2)3 – 7(2)2 – 3(2) + 18
= 16 – 28 – 6 + 18 = 0
Hence, (x – 2) is a factor of f(x).
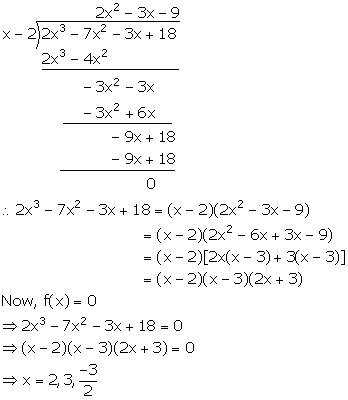
Question 5
Given that x – 2 and x + 1 are factors of f(x) = x3 + 3x2 + ax + b; calculate the values of a and b. Hence, find all the factors of f(x).
Answer 5
f(x) = x3 + 3x2 + ax + b
Since, (x – 2) is a factor of f(x), f(2) = 0
(2)3 + 3(2)2 + a(2) + b = 0
8 + 12 + 2a + b = 0
2a + b + 20 = 0 …(i)
Since, (x + 1) is a factor of f(x), f(-1) = 0
(-1)3 + 3(-1)2 + a(-1) + b = 0
-1 + 3 – a + b = 0
-a + b + 2 = 0 …(ii)
Subtracting (ii) from (i), we get,
3a + 18 = 0
a = -6
Substituting the value of a in (ii), we get,
b = a – 2 = -6 – 2 = -8
f(x) = x3 + 3x2 – 6x – 8
Now, for x = -1,
f(x) = f(-1) = (-1)3 + 3(-1)2 – 6(-1) – 8 = -1 + 3 + 6 – 8 = 0
Hence, (x + 1) is a factor of f(x).
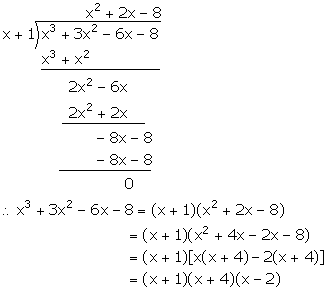
Question 6
The expression 4x3 – bx2 + x – c leaves remainders 0 and 30 when divided by x + 1 and 2x – 3 respectively. Calculate the values of b and c. Hence, factorise the expression completely.
Answer 6
Let f(x) = 4x3 – bx2 + x – c
It is given that when f(x) is divided by (x + 1), the remainder is 0.
f(-1) = 0
4(-1)3 – b(-1)2 + (-1) – c = 0
-4 – b – 1 – c = 0
b + c + 5 = 0 …(i)
It is given that when f(x) is divided by (2x – 3), the remainder is 30.
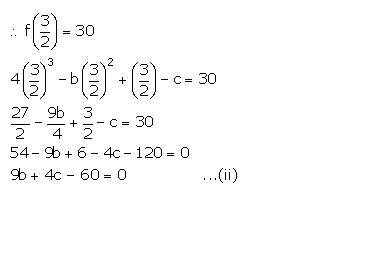
Multiplying (i) by 4 and subtracting it from (ii), we get,
5b + 40 = 0
b = -8
Substituting the value of b in (i), we get,
c = -5 + 8 = 3
Therefore, f(x) = 4x3 + 8x2 + x – 3
Now, for x = -1, we get,
f(x) = f(-1) = 4(-1)3 + 8(-1)2 + (-1) – 3 = -4 + 8 – 1 – 3 = 0
Hence, (x + 1) is a factor of f(x).
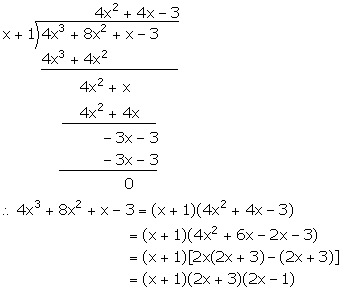
Question 7
If x + a is a common factor of expressions f(x) = x2 + px + q and g(x) = x2 + mx + n; show that:
Answer 7
f(x) = x2 + px + q
It is given that (x + a) is a factor of f(x).
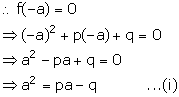
g(x) = x2 + mx + n
It is given that (x + a) is a factor of g(x).

From (i) and (ii), we get,
pa – q = ma – n
n – q = a(m – p)
![]()
Hence, proved.
Question 8
The polynomials ax3 + 3x2 – 3 and 2x3 – 5x + a, when divided by x – 4, leave the same remainder in each case. Find the value of a.
Answer 8
Let f(x) = ax3 + 3x2 – 3
When f(x) is divided by (x – 4), remainder = f(4)
f(4) = a(4)3 + 3(4)2 – 3 = 64a + 45
Let g(x) = 2x3 – 5x + a
When g(x) is divided by (x – 4), remainder = g(4)
g(4) = 2(4)3 – 5(4) + a = a + 108
It is given that f(4) = g(4)
64a + 45 = a + 108
63a = 63
a = 1
Question 9
Find the value of ‘a’, if (x – a) is a factor of x3 – ax2 + x + 2.
Solution 9
Let f(x) = x3 – ax2 + x + 2
It is given that (x – a) is a factor of f(x).
Remainder = f(a) = 0
a3 – a3 + a + 2 = 0
a + 2 = 0
a = -2
Question 10
Find the number that must be subtracted from the polynomial 3y3 + y2 – 22y + 15, so that the resulting polynomial is completely divisible by y + 3.
Solution 10
Let the number to be subtracted from the given polynomial be k.
Let f(y) = 3y3 + y2 – 22y + 15 – k
It is given that f(y) is divisible by (y + 3).
Remainder = f(-3) = 0
3(-3)3 + (-3)2 – 22(-3) + 15 – k = 0
-81 + 9 + 66 + 15 – k = 0
9 – k = 0
k = 9
Selina Concise Maths Solution Exercise – 8(C) Remainder And Factor Theorems
Question 1
Show that (x – 1) is a factor of x3 – 7x2 + 14x – 8. Hence, completely factorise the given expression.
Answer 1
Let f(x) = x3 – 7x2 + 14x – 8
f(1) = (1)3 – 7(1)2 + 14(1) – 8 = 1 – 7 + 14 – 8 = 0
Hence, (x – 1) is a factor of f(x).
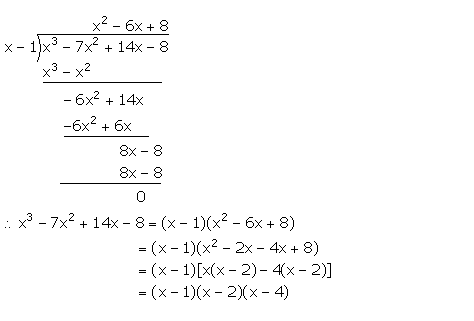
Question 2
Using Remainder Theorem, factorise:
x3 + 10x2 – 37x + 26 completely.
Answer 2

Question 3
When x3 + 3x2 – mx + 4 is divided by x – 2, the remainder is m + 3. Find the value of m.
Answer 3
Let f(x) = x3 + 3x2 – mx + 4
According to the given information,
f(2) = m + 3
(2)3 + 3(2)2 – m(2) + 4 = m + 3
8 + 12 – 2m + 4 = m + 3
24 – 3 = m + 2m
3m = 21
m = 7
Question 4
What should be subtracted from 3x3 – 8x2 + 4x – 3, so that the resulting expression has x + 2 as a factor?
Answer 4
Let the required number be k.
Let f(x) = 3x3 – 8x2 + 4x – 3 – k
According to the given information,
f (-2) = 0
3(-2)3 – 8(-2)2 + 4(-2) – 3 – k = 0
-24 – 32 – 8 – 3 – k = 0
-67 – k = 0
k = -67
Thus, the required number is -67.
Question 5
If (x + 1) and (x – 2) are factors of x3 + (a + 1)x2 – (b – 2)x – 6, find the values of a and b. And then, factorise the given expression completely.
Answer 5
Let f(x) = x3 + (a + 1)x2 – (b – 2)x – 6
Since, (x + 1) is a factor of f(x).
Remainder = f(-1) = 0
(-1)3 + (a + 1)(-1)2 – (b – 2) (-1) – 6 = 0
-1 + (a + 1) + (b – 2) – 6 = 0
a + b – 8 = 0 …(i)
Since, (x – 2) is a factor of f(x).
Remainder = f(2) = 0
(2)3 + (a + 1) (2)2 – (b – 2) (2) – 6 = 0
8 + 4a + 4 – 2b + 4 – 6 = 0
4a – 2b + 10 = 0
2a – b + 5 = 0 …(ii)
Adding (i) and (ii), we get,
3a – 3 = 0
a = 1
Substituting the value of a in (i), we get,
1 + b – 8 = 0
b = 7
f(x) = x3 + 2x2 – 5x – 6
Now, (x + 1) and (x – 2) are factors of f(x). Hence, (x + 1) (x – 2) = x2 – x – 2 is a factor of f(x).
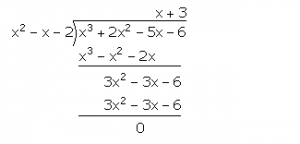
f(x) = x3 + 2x2 – 5x – 6 = (x + 1) (x – 2) (x + 3)
Question 6
If x – 2 is a factor of x2 + ax + b and a + b = 1, find the values of a and b.
Answer 6
Let f(x) = x2 + ax + b
Since, (x – 2) is a factor of f(x).
Remainder = f(2) = 0
(2)2 + a(2) + b = 0
4 + 2a + b = 0
2a + b = -4 …(i)
It is given that:
a + b = 1 …(ii)
Subtracting (ii) from (i), we get,
a = -5
Substituting the value of a in (ii), we get,
b = 1 – (-5) = 6
Question 7
Factorise x3 + 6x2 + 11x + 6 completely using factor theorem.
Answer 7
Let f(x) = x3 + 6x2 + 11x + 6
For x = -1
f(-1) = (-1)3 + 6(-1)2 + 11(-1) + 6
= -1 + 6 – 11 + 6 = 12 – 12 = 0
Hence, (x + 1) is a factor of f(x).
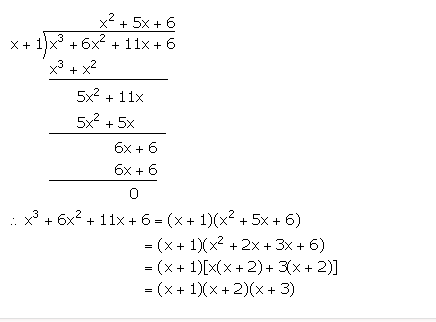
Question 8
Find the value of ‘m’, if mx3 + 2x2 – 3 and x2 – mx + 4 leave the same remainder when each is divided by x – 2.
Answer 8
Let f(x) = mx3 + 2x2 – 3
g(x) = x2 – mx + 4
It is given that f(x) and g(x) leave the same remainder when divided by (x – 2). Therefore, we have:
f (2) = g (2)
m(2)3 + 2(2)2 – 3 = (2)2 – m(2) + 4
8m + 8 – 3 = 4 – 2m + 4
10m = 3
m =3/8
Question 9
The polynomial px3 + 4x2 – 3x + q is completely divisible by x2 – 1; find the values of p and q. Also, for these values of p and q factorize the given polynomial completely.
Answer 9 Remainder And Factor Theorems
Let f(x) = px3 + 4x2 – 3x + q
It is given that f(x) is completely divisible by (x2 – 1) = (x + 1)(x – 1).
Therefore, f(1) = 0 and f(-1) = 0
f(1) = p(1)3 + 4(1)2 – 3(1) + q = 0
p + q + 1 = 0 …(i)
f(-1) = p(-1)3 + 4(-1)2 – 3(-1) + q = 0
-p + q + 7 = 0 …(ii)
Adding (i) and (ii), we get,
2q + 8 = 0
q = -4
Substituting the value of q in (i), we get,
p = -q – 1 = 4 – 1 = 3
f(x) = 3x3 + 4x2 – 3x – 4
Given that f(x) is completely divisible by (x2 – 1).
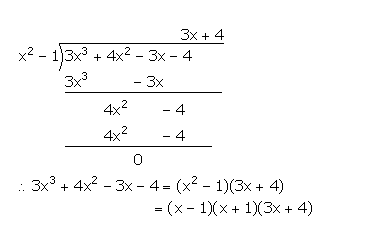
Question 10
Find the number which should be added to x2 + x + 3 so that the resulting polynomial is completely divisible by (x + 3).
Answer 10
Let the required number be k.
Let f(x) = x2 + x + 3 + k
It is given that f(x) is divisible by (x + 3).
Remainder = 0
f (-3) = 0
(-3)2 + (-3) + 3 + k = 0
9 – 3 + 3 + k = 0
9 + k = 0
k = -9
Thus, the required number is -9.
Question 11 Remainder And Factor Theorems
When the polynomial x3 + 2x2 – 5ax – 7 is divided by (x – 1), the remainder is A and when the polynomial x3 + ax2 – 12x + 16 is divided by (x + 2), the remainder is B. Find the value of ‘a’ if 2A + B = 0.
Answer 11
It is given that when the polynomial x3 + 2x2 – 5ax – 7 is divided by (x – 1), the remainder is A.
(1)3 + 2(1)2 – 5a(1) – 7 = A
1 + 2 – 5a – 7 = A
– 5a – 4 = A …(i)
It is also given that when the polynomial x3 + ax2 – 12x + 16 is divided by (x + 2), the remainder is B.
x3 + ax2 – 12x + 16 = B
(-2)3 + a(-2)2 – 12(-2) + 16 = B
-8 + 4a + 24 + 16 = B
4a + 32 = B …(ii)
It is also given that 2A + B = 0
Using (i) and (ii), we get,
2(-5a – 4) + 4a + 32 = 0
-10a – 8 + 4a + 32 = 0
-6a + 24 = 0
6a = 24
a = 4
Question 12
(3x + 5) is a factor of the polynomial (a – 1)x3 + (a + 1)x2 – (2a + 1)x – 15. Find the value of ‘a’, factorise the given polynomial completely.
Answer 12
Let f(x) = (a – 1)x3 + (a + 1)x2 – (2a + 1)x – 15
It is given that (3x + 5) is a factor of f(x).
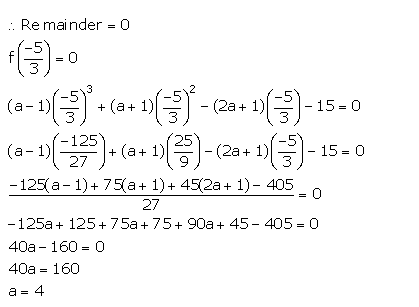
f(x) = (a – 1)x3 + (a + 1)x2 – (2a + 1)x – 15
= 3x3 + 5x2 – 9x – 15
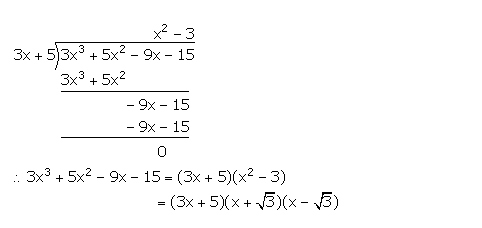
Question 13 Remainder And Factor Theorems
When divided by x – 3 the polynomials x3 – px2 + x + 6 and 2x3 – x2 – (p + 3) x – 6 leave the same remainder. Find the value of ‘p’.
Answer 3
If (x – 3) divides f(x) = x3 – px2 + x + 6, then,
Remainder = f(3) = 33 – p(3)2 + 3 + 6 = 36 – 9p
If (x – 3) divides g(x) = 2x3 – x2 – (p + 3) x – 6, then
Remainder = g(3) = 2(3)3 – (3)2 – (p + 3) (3) – 6 = 30 – 3p
Now, f(3) = g(3)
36 – 9p = 30 – 3p
-6p = -6
p = 1
Question 14 Remainder And Factor Theorems
Use the Remainder Theorem to factorise the following expression:
2x3 + x2 – 13x + 6
Answer 14
f(x) = 2x3 + x2 – 13x + 6
Factors of constant term 6 are 1, 2, 3, 6.
Putting x = 2, we have:
f(2) = 2(2)3 + 22 – 13 (2) + 6 = 16 + 4 – 26 + 6 = 0
Hence (x – 2) is a factor of f(x).
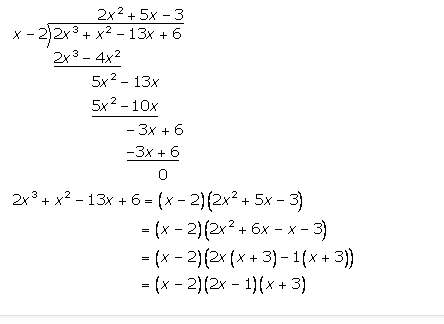
Question 15
Using remainder theorem, find the value of k if on dividing 2x3 + 3x2 – kx + 5 by x – 2, leaves a remainder 7.
Answer 15
Let f(x) = 2x3 + 3x2 – kx + 5
Using Remainder Theorem, we have
f(2) = 7
∴ 2(2)3 + 3(2)2 – k(2) + 5 = 7
and ∴ 16 + 12 – 2k + 5 = 7
so ∴ 33 – 2k = 7
Therefor ∴ 2k = 26
Hence ∴ k = 13
Question 16
What must be subtracted from 16x3 – 8x2 + 4x + 7 so that the resulting expression has 2x + 1 as a factor?
Answer 16
Here, f(x) = 16x3 – 8x2 + 4x + 7
Let the number subtracted be k from the given polynomial f(x).
Given that 2x + 1 is a factor of f(x).
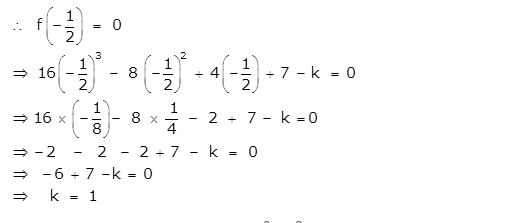
Therefore 1 must be subtracted from 16x3 – 8x2 + 4x + 7 so that the resulting expression has 2x + 1 as a factor.
———-End of Remainder And Factor Theorems—–
Return to :- Concise Selina Maths Solutions for ICSE Class-10
Thanks
Please share with your friends