Rest and Motions Exercise Questions Solutions HC Verma Ch-3 Concept of Physics Vol-1 for Class-11. Step by Step Solution of Exercise Questions for Ch-3 Rest and Motions Kinematics HC Verma Concept of Physics . Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Rest and Motions Exercise Questions Solutions HC Verma Ch-3 Concept of Physics Vol-1 for Class-11
| Board | ISC and other board |
| Publications | Bharti Bhawan Publishers |
| Ch-3 | Rest and Motions Kinematics |
| Class | 11 |
| Vol | 1st |
| writer | H C Verma |
| Book Name | Concept of Physics |
| Topics | Solution of Exercise Questions |
| Page-Number | 51, 52, 53, 54 |
-: Select Topics :-
Exercise (Currently Open)
HC Verma Solutions of Ch-3 Rest and Motions Exercise Questions
(Page-51)
Question-1
A man has to go 50 m due north, 40 m due east and 20 m due south to reach a field.
(a) What distance he has to walk to reach the field?
(b) What is his displacement from his house to the field?
Answer-1
(a) Distance travelled by the man = AB + BC + CD = 50 + 40 + 20 = 110 m
(b) AF = AB − BF = 50 − 20 = 30 m
Displacement = Final position − Initial position = AD

Question-2
A particle starts from the origin, goes along the X-axis to the point (20 m, 0) and then return along the same line to the point (−20 m, 0). Find the distance and displacement of the particle during the trip.
Answer-2
Let the points be O(0,0), A(20 m, 0) and B(−20 m, 0).
(i) Distance travelled = OA + AB = 20 + 40 = 60 m
(ii) Displacement = OB = 20 m (in the negative direction)
Question-3
It is 260 km from Patna to Ranchi by air and 320 km by road. An aeroplane takes 30 minutes to go from Patna to Ranchi whereas a delux bus takes 8 hours.
(a) Find the average speed of the plane.
(b) Find the average speed of the bus.
(c) Find the average velocity of the plane.
(d) Find the average velocity of the bus.
Answer-3
(a)

(b)

(c)
The plane moves in a straight path.
Average velocity = Average speed = 520 Km / h (Patna to Ranchi)
(d) Straight path distance from Patna to Ranchi = Displacement of the bus = 260 km

Question-4
When a person leaves his home for sightseeing by his car, the meter reads 12352 km. When he returns home after two hours the reading is 12416 km
(a) What is the average speed of the care during this period?
(b) What is the average of velocity?
Answer-4
(a) Total distance covered = 12416 − 12352 = 64 km
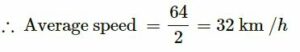
(b) Because he returns to his house, the displacement is zero. So, the average velocity is zero
Question-5
An athlete takes 2.0 s to reach his maximum speed of 18.0 km/h. What is the magnitude of this average acceleration.
Answer-5
Initial velocity, u = 0
Final velocity, v = 18 km/h = 5 m/s
Time interval, t = 2 s
Using
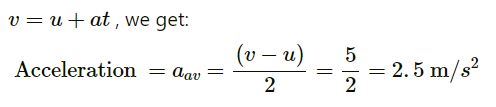
Question-6
The speed of a car as a function of time is shown in the following figure. Find the distance travelled by the car in 8 seconds and its acceleration.

Figure-3-E.1
Answer-6
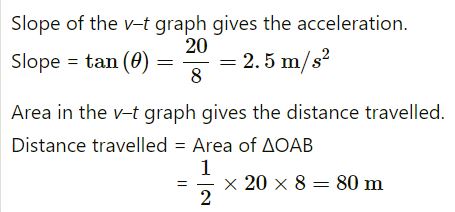
Question-7
The acceleration of a cart started at t = 0, varies with time as shown in the following figure. Find the distance travelled in 30 seconds and draw the position-time graph
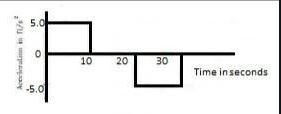
Figure-3-E.2
Answer-7
In the first 10 seconds,
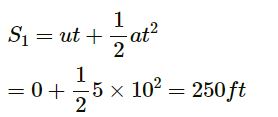
At t = 10 s,
v = u + at = 0 + 5 × 10 = 50 ft/s
∴ From 10 to 20 seconds (∆t = 20 − 10 = 10 s), the particle moves with a uniform velocity of 50 ft/s.
Distance covered from t = 10 s to t = 20 s:
S2 = 50 × 10 = 500 ft
Between 20 s to 30 s, acceleration is constant, i.e., −5 ft/s2.
At 20 s, velocity is 50 ft/s.
t = 30 − 20 = 10 s
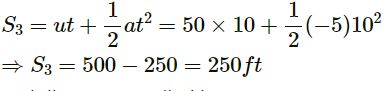
Total distance travelled is 30 s:
S1 + S2 + S3
= 250 + 500 + 250
= 1000 ft
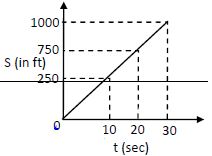
The position–time graph:
Question-8
Figure (3 -E.3) Shows the graph of velocity versus time for a particle going along the X-axis.

(a )Find the acceleration
(b) Find the distance travelled in 0 to 10s and
(c) Find the displacement in 0 to 10 s.
Answer-8
(a )
Slope of the v–t graph gives the acceleration.
Acceleration
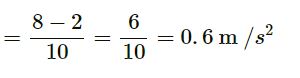
(b)
Area in the v–t graph gives the distance travelled.
Distance travelled = Area of ∆ABC + Area of rectangle OABD
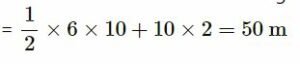
(c)
Displacement is the same as the distance travelled.
Displacement = 50 m
Question-9
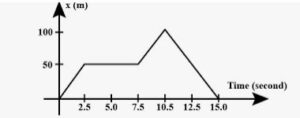
Figure (3 -E.4) shows the graph of the x-coordinate of a particle going along the X-axis as a function of time.
(a) Find the average velocity during 0 to 10 s,
(b) Find instantaneous velocity at 2, 5, 9 and 12s.
Answer-9
(a)
Displacement from t = 0 s to t = 10 s:
x = 100 m
Time = 10 s
Average velocity from 0 to 10 seconds,

(b)
Slope of the x–t graph gives the velocity.
At 2.5 s,
slope =
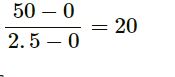
⇒ vinst = 20 m/s
At 5 s, vinst = 0.
At 8 s, vinst = 20 m/s.
At 12 s, vinst = −20 m/s.
Question-10
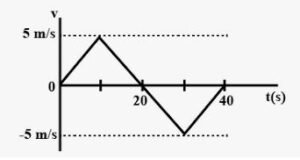
From the velocity-time plot shown in figure,(3 -E.5) find the distance travelled by the particle during the first 40 seconds. Also find the average velocity during this period
Answer-10
Area shown in the v–t graph gives the distance travelled.
∴ Distance travelled in the first 40 seconds = Area of ∆OAB + Area of ∆BCD
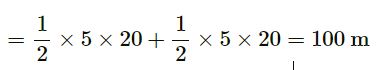
As the displacement is zero, the average velocity is zero.
HC Verma Solutions of Ch-3 Rest and Motions Exercise Questions
(Page-52)
Question-11
figure (3 -E.6) shows x-t graph of a particle. Find the time t such that the average velocity of the particle during the period 0 to t is zero.
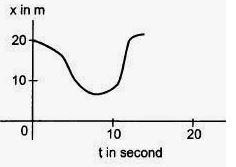
(3 -E.6)
Answer-11
Consider point B1 at 12 s.
At t = 0 s, S = 20 m and at t = 12 s, S = 20 m.
For the time interval 0–12, change in the displacement is zero.
Hence, the time is 12 seconds.
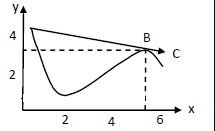
Question-12
A particle starts from a point A and travels along the solid curve shown in figure (3 -E.7) . Find approximately the position B of the particle such that the average velocity between the position A and B has the same direction as the instantaneous velocity at B.
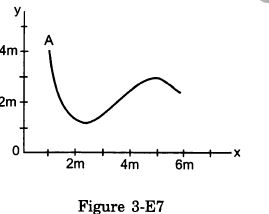
Answer-12
At position B , the instantaneous velocity of the particle has the direction along BC

Question-13
An object having a velocity 4.0 m/s is accelerated at the rate of 1.2 m/s2 for 5.0 s. Find the distance travelled during the period of acceleration.
Answer-13
Given:
Velocity, u = 4.0 m/s
Acceleration, a = 1.2 m/s2
Time, t = 5.0 s
Distance travelled :
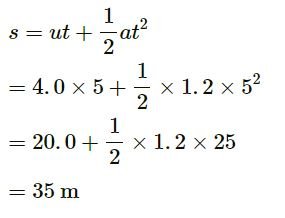
Question-14
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
Answer-14
Initial velocity, u = 43.2 km/h = 12 m/s
Final velocity, v = 0
Acceleration, a = −6 m/s2
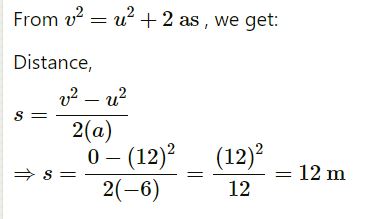
Question-15
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find
(a) the total distance moved by the train
(b) the maximum speed attained by the train .
(c) the position(s) of the train at half the maximum speed.
Answer-15
(a)
Initial velocity, u = 0
Acceleration, a = 2 m/s2
Let the final velocity be v before the brakes are applied.
Now,
t = 30 s
v = u + at
v = 0 + 2 × 30
⇒ v = 60 m/s
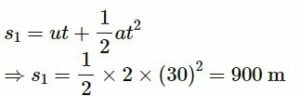
When the brakes are applied:
u‘ = 60 m/s
v‘ = 0
t = 1 min = 60 s
Acceleration:
s = s1 +s2 = 1800 + 900 = 2700 m
⇒ s = 2.7 km
(b)
Initial velocity, u = 0
Acceleration, a = 2 m/s2
Let the final velocity be v before the brakes are applied.
Now,
t = 30 s
v = u + at
v = 0 + 2 × 30
⇒ v = 60 m/s
Maximum speed attained by the train, v = 60 m/s
(c)
Initial velocity, u = 0
Acceleration, a = 2 m/s2
Let the final velocity be v before the brakes are applied.
Now,
t = 30 s
v = u + at
v = 0 + 2 × 30
⇒ v = 60 m/s
Half the maximum speed =60 / 2=30 m /s
When the train is accelerating with an acceleration of 2 m/s2:
Distance,
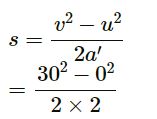
When the train is decelerating with an acceleration of – 1 m/s2:
Distance,

Position from the starting point
Question-16
A bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
Answer-16
Initial velocity, u = 16 m/s
Final velocity, v = 0
Distance, s = 0.4 m
Acceleration,

Question-17
A bullet going with speed 350 m/s enters a concrete wall and penetrates a distance of 5.0 cm before coming to rest. Find the deceleration.
Answer-17
Initial velocity, u = 350 m/s
Final velocity, v = 0
Distance travelled by the bullet before coming to rest, s = 5 m

Question-18
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find
(a ) the average velocity during this period .
(b) distance travelled by the particle during this period.
Answer-18
(a )
Initial velocity of the particle, u = 0
Final velocity of the particle, v = 18 km/h = 5 m/s
Time, t = 5 s
Acceleration, a = (v − u) /t
⇒ a = (5 − 0) /5 = 1 m/s2
Distance,

Final velocity of the particle, v = 18 km/h = 5 m/s
Time, t = 5 s
Acceleration, a = (v − u) /t
⇒ a = (5 − 0) /5 = 1 m/s2
Distance,

Question-19
A driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he is driving a car at a speed of 54 km/h and the brakes cause a deceleration of 6.0 m/s2, find the distance travelled by the car after he sees the need to put the brakes on.
Answer-19
In the reaction time, the car moves with a constant speed of 54 km/h, i.e., 15 m/s.
Distance travelled in this time, s1 = 15 × 0.2 = 3 m
When the brakes are applied:
Initial velocity of the car, u = 15 m/s
Final velocity of the car, v = 0
Acceleration, a = −6 m/s2
Distance,
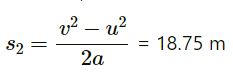
⇒ s = 3 + 18.75 = 21.75 m
⇒ 22 m
Question-20
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ………… Total stopping distance b = ………… |
Speed = 72 km/h Braking distance c = ……….. Total stopping distance d = ………… |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ……….. Total stopping distance f = ………… |
Speed 72 km/h Braking distance g = …………. Total stopping distance h = ………… |
Answer-20
Braking distance: Distance travelled after the brakes are applied.
Total stopping distance = Braking distance + Distance travelled in the reaction time
Case A:
Deceleration = 6.0 m/s2
For driver X:
Initial velocity, u = 54 km/h= 15 m/s
Final velocity, v = 0
Braking distance,

Distance travelled in the reaction time = 15 × 0.20 = 3 m
Total stopping distance, b = 19 + 3 = 22 m
For driver Y:
Initial velocity, u = 72 km/h= 20 m/s
Final velocity, v = 0
Braking distance,
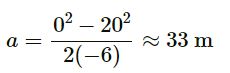
Total stopping distance, d = 33 + 6 = 39 mCase B:
Deceleration = 6.0 m/s2
Now, we have:
e = 15 m
f = 18 m
g = 27 m
h = 33 m
| Car Model | Driver X Reaction Time = 0.20 s |
Driver Y Reaction Time = 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance, a = 19 m Total stopping distance, b = 22 m |
Speed = 72 km/h Braking distance, c = 33 m Total stopping distance, d = 39 m |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance, e = 15 m Total stopping distance, f = 18 m |
Speed = 72 km/h Braking distance, g = 27 m Total stopping distance, h = 33 m |
Question-21
Answer-21
Velocity of the culprit riding the motor bike,vc = 72 km/h = 20 m/s

In 10 seconds, the culprit reaches point B from point A.
Distance covered by the culprit:
s = vct = 20 × 10 = 200 m
At time t = 10 s, the police jeep is 200 m behind the culprit.
Relative velocity between the police jeep and the culprit:
25 − 20 = 5 m/s
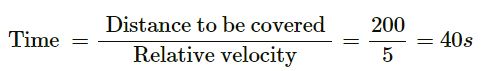
In 40 seconds, the police jeep moves from point A to a distance s‘ to catch the culprit.
Here,
s‘ = vpt = 25 × 40
⇒ s‘ = 1000 m = 1.0 km
Thus, the jeep will catch up with the bike 1.0 km away from the turning
Question-22
Answer-22
Velocity of the first car, v1= 60 km/h = 16.7 m/s
Velocity of the second car, v2 = 42 km/h = 11.7 m/s
Relative velocity between the cars = (16.7 − 11.7) = 5 m/s
Distance travelled by the first car w.r.t. the second car = 5 + 5 = 10 m
Time,
The first car also covers a distance equal to its own length = 5 m
∴ Total road distance used for the overtake = 33.4 + 5 = 38 m
Question-23
Answer-23
Initial speed of the ball, u = 50 m/s
Acceleration, a = −10 m/s2
At the highest point, velocity v of the ball is 0.

Initial speed of the ball, u = 50 m/s
Acceleration, a = −10 m/s2
At the highest point, velocity v of the ball is 0.

Initial speed of the ball, u = 50 m/s
Acceleration, a = −10 m/s2
At the highest point, velocity v of the ball is 0

Question-24
Answer-24
Given:
Height of the balloon from the ground, s = 60 m
Balloon is moving upwards with velocity 7 m/s.
The balloon and the ball are moving upwards with the same speed.
When the ball is dropped, its initial velocity (u) is −7 m/s.
Acceleration due to gravity, a = g = 9.8 m/s2
Using the equation of motion, we have:
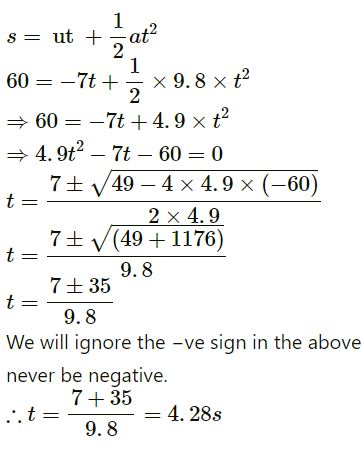
Question-25
Answer-25
Given:
Initial velocity with which the stone is thrown vertically upwards, u = 28 m/s
When the stone reaches the ground, its final velocity (v) is 0.
Also,
a = g = −9.8 m/s2 (Acceleration due to gravity)
Maximum height can be found using the equation of motion.
Thus, we have:

Given:
Initial velocity with which the stone is thrown vertically upwards, u = 28 m/s
When the stone reaches the ground, its final velocity (v) is 0.
Also,
a = g = −9.8 m/s2 (Acceleration due to gravity)
Total time taken by the stone to reach the maximum height:
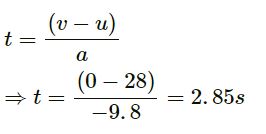
As per the question, we need to find the velocity of the stone one second before it reaches the maximum height.
t’ = 2.85 − 1 = 1.85 s
Again, using the equation of motion, we get:
v’ = u + at’ = 28 − 9.8 × 1.85
⇒ v’ = 28 − 18.13 = 9.87 m/s
Hence, the velocity is 9.87 m/s
Given:
Initial velocity with which the stone is thrown vertically upwards, u = 28 m/s
When the stone reaches the ground, its final velocity (v) is 0.
Also,
a = g = −9.8 m/s2 (Acceleration due to gravity)
will not change, as after one second, the velocity becomes zero for any initial velocity and acceleration (a = − 9.8 m/s2) remains the same. For any initial velocity more than 28 m/s, only the maximum height increases.
Question-26
Answer-26
A person is releasing balls from a tall building at regular intervals of one second.
It means for each ball, the initial velocity u is 0.
Acceleration due to gravity, a = g = 9.8 m/s2
When the 6th ball is dropped, the 5th ball moves for 1 second, the 4th ball moves for 2 seconds and the 3rdball moves for 3 seconds.
Position of the 3rd ball after t = 3 s:
Using the equation of motion, we get:

Rest and Motions Exercise Questions Solution HC Verma of Ch-3
(Page-53)
Question-27
Answer-27
Height of the building = 11.8 m
Distance of the young man from the building = 7 m
The kid should be caught over 1.8 m from ground.
As the kid is slipping, his initial velocity u is 0.
Acceleration, a = 9.8 m/s2
Let s be the distance before which the kid has to be caught = 11.8 − 1.8 = 10 m
Using the equation of motion, we get:

This is the time in which the man should reach the bottom of the building to catch the kid.
Velocity with which the man should run:
s / t = 7 / 1.42 = 4.9 m / s
Question-28
Answer-28
Distance of the bird from the ground, s = 12.1 m
Initial velocity of the berry dropped by the bird, u = 0
Acceleration due to gravity, a = g = 9.8 m/s2
Using the equation of motion, we can find the time taken t by the berry to reach the ground.
Thus

Therefore, the cadet who is 2.6 m away from tree will receive the berry on his uniform.
Question 29:
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
Answer-29
Given:
Distance travelled by the ball in 0.200 seconds = 6 m
Let:
Time, t = 0.200 s
Distance, s = 6 m
a = g = 10 m/s2 (Acceleration due to gravity)
Using the equation of motion, we get:
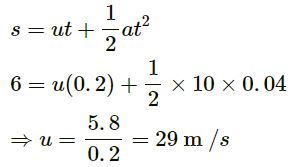
Let h be the height from which the ball is dropped.
We have:
u = 0 and v = 29 m/s
Now,
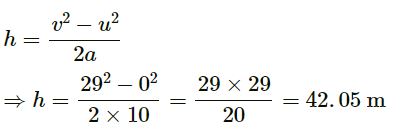
∴ Total height = 42.05 + 6 = 48.05 m ≈ 48 m
Question 30:
A ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball is sand assuming it to be uniform.
Answer-30
A ball is dropped from a height of 5 m (s) above the sand level.
The same ball penetrates the sand up to 10 cm (ss) before coming to rest.
Initial velocity of the ball, u = 0 And,
a = g = 9.8 m/s2 (Acceleration due to gravity)
Using the equation of motion, we get :
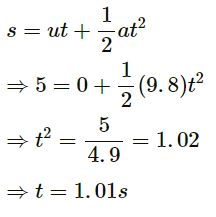
Thus, the time taken by the ball to cover the distance of 5 m is 1.01 seconds.
Velocity of the ball after 1.01 s:
v = u + at
⇒ v = 9.8 × 1.01 = 9.89 m/s
Hence, for the motion of the ball in the sand, the initial velocity u2should be 9.89 m/s and the final velocity v2 should be 0.
ss = 10 cm = 0.1 m
Again using the equation of motion, we get:

Hence, the sand offers the retardation of 490 m/s2.
Question 31:
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
Answer-31
Given:
Distance between the coin and the floor of the elevator before the coin is dropped = 6 ft
Let a be the acceleration of the elevator.
It is given that the coin reaches the floor in 1 second. This means that the coin travels 6 ft distance.
The initial velocity is u for the coin and zero for the elevator.
Using the equation of motion, we get:
Equation for the coin :
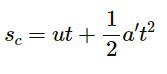
Here,
a‘ = g − a ( a‘ is the acceleration felt by the coin.)
g = Acceleration due to gravity
g = 9.8 m/s2 = 32 ft/s2
On substituting the values, we get
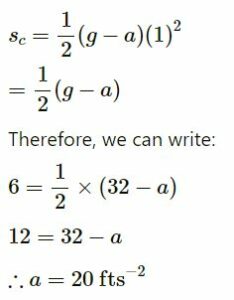
Hence, the acceleration of the elevator is 20 ft/s2.
Question 32:
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find
(a) the time it takes to reach the ground,
(b) the horizontal distance it travels before reaching the ground,
(c) the velocity (direction and magnitude) with which it strikes the ground.
Answer-32
(a)

Given:
Speed of the ball, ux = 20 m/s
Height from which the ball is dropped, h = 100 m
Let t be the time taken by the ball to reach the ground.
Using the equation of motion, we have:

Here,
Acceleration of gravity, g = 9.8 ms−2
Vertical component of velocity, uy = 0
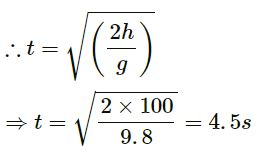
Therefore, the time required by the ball to reach the ground is 4.5 seconds.
(b)

Given:
Speed of the ball, ux = 20 m/s
Height from which the ball is dropped, h = 100 m
Horizontal distance travelled by the ball:
x = uxt = 20 × 4.5 = 90 m
(c)

Given:
Speed of the ball, ux = 20 m/s
Height from which the ball is dropped, h = 100 m
We know that horizontal velocity remains constant throughout the motion of the ball.
At A, vx = 20 m/s.
vy = u + gt = 0 + 9.8 × 4.5
⇒vy = 44.1 m/s
Resultant velocity:
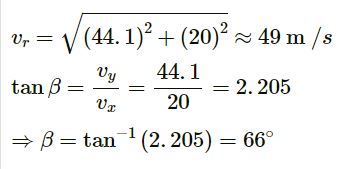
Therefore, the ball strikes the ground with a magnitude of velocity 49 m/s and the direction at an angle of 66° with the ground.
Question 33:
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find
(a) the maximum height reached and
(b) the range of the ball. Take g = 10 m/s2.
Answer-33
(a)
Given:
Initial speed of the ball, u = 40 m/s
Angle of projection of the ball with the horizontal, α = 60°
Also,
a = g = 10 m/s2
Maximum height reached by the ball:
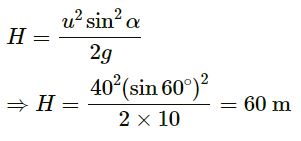
(b)
Given:
Initial speed of the ball, u = 40 m/s
Angle of projection of the ball with the horizontal, α = 60°
Also,
a = g = 10 m/s2
Horizontal range of the ball:

Question 34:
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
Answer-34
Given:
Height of the goalpost = 10 ft
The football is kept at a distance of 40 yards, i.e., 120 ft, from the goalpost.
Initial speed u with which the ball is hit = 64 ft/s
Acceleration due to gravity, a = g = 9.8 m/s2 = 32.2 ft/s2
For the given question, 40 yards is the horizontal range (R).
Angle of projection, α = 45°
We know that the horizontal range is given by
R = u cos α(t)

= 6.86 ft < Height of the goalpost
Yes, the football will reach the goalpost
Question 35
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of 2.0 m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationery goli without falling on the ground earlier?
Answer-35
Given:
Distance between the golis of the first and second players = 2.0 m = R = Horizontal range
Height h from which the goli is projected by the second player = 19.6 cm = 0.196 m
We know that the goli moves in projectile motion.
Acceleration due to gravity a = g = 9.8 m/s2
The time in which the goli will reach the ground is given by the equation of motion.
As the initial velocity uy in vertical direction is zero, we have:

Let us assume that the goli is projected with horizontal velocity ux m/s
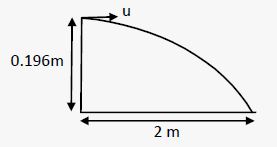
The horizontal range is given by
R = uxt
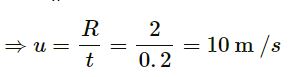
Hence, if the second player projects the goli with a speed of 10 m/s, then his goli will hit the goli of the first player.
Question 36:
Figure (3−E8) shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
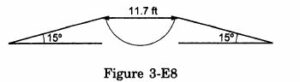
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
Answer-36
Given:
Width of the ditch = 11.7 ft
Length of the bike = 5 ft
The approach road makes an angle of 15˚ (α) with the horizontal.
Total horizontal range that should be covered by the biker to cross the ditch safely, R = 11.7 + 5 = 16.7 ft
Acceleration due to gravity, a = g = 9.8 m/s = 32.2 ft/s2
We know that the horizontal range is given by

⇒ u =32ft/s
Therefore, the minimum speed with which the motorbike should be moving is 32 ft/s.
Question 37:
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
Answer-37
Given:
Height (h) of the cliff = 171 ft
Horizontal distance from the bottom of the cliff = 228 ft
As per the question, the person throws the packet directly aiming to his friend at the initial speed (u) of 15.0 ft/s.
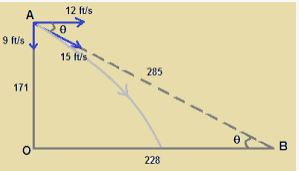

∴ θ = 37°
When the person throws the packet from the top of the cliff, it moves in projectile motion.
Let us take the reference axis at point A.
u is below the x-axis.
a = g = 32.2 ft/s2 (Acceleration due to gravity)
Using the second equation of motion, we get:

Question 38:
A ball is projected from a point on the floor with a speed of 15 m/s at an angle of 60° with the horizontal. Will it hit a vertical wall 5 m away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is 22 m away?
Answer-38
Given:
Initial speed of the ball, u = 15 m/s
Angle of projection with horizontal, α = 60°
Distance of the wall from the point of projection = 5 m
a = g = 9.8 m/s2 (Acceleration due to gravity)
We know that the horizontal range for a projectile is given by
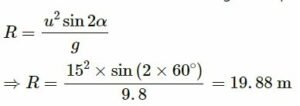
As the horizontal range of the projectile is 19.88 m, the ball will hit the wall 5 m away from the point of projection. If the wall is 22 m away from the point of projection, the ball will hit the wall because it is not in its horizontal range.
Question 39:
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
Answer-39
Given:
Initial velocity of the projectile = u
Angle of projection = θ
To find: Average velocity of the projectile
Average velocity

So, there will be no effect of the vertical component of velocity of the projectile during displacement AB.
We know that the projectile moves at a constant velocity u cos θ in horizontal direction.
Hence, the average velocity of the projectile is u cos θ.
Question 40:
A bomb is dropped from a plane flying horizontally with uniform speed. Show that the bomb will explode vertically below the plane. Is the statement true if the plane flies with uniform speed but not horizontally?
Answer-40
Case-1 plane flying horizontally with uniform speed
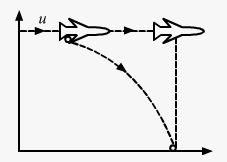
The plane is flying horizontally with a uniform speed. Therefore, the bomb also has the same speed.
Let the speed of the plane be represented by u.
Now, let t be the time taken by the bomb to reach the ground.
Distance travelled by the bomb in horizontal direction = ut
Both the plane and bomb are travelling in the same direction.
Distance travelled by the plane in the same time = ut
Hence, the bomb will explode vertically below the plane.
Case-2 plane flies with uniform speed but not horizontally
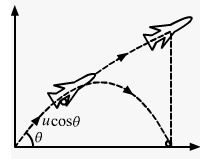
When the plane is flying with a uniform speed but not horizontally:
Let us consider it will make an angle of projection θ along the horizontal direction.
So, both the plane and the bomb will be flying with the same angle of projection.
Therefore, both will have the same horizontal speed u cos θ, where u is the initial speed of the plane and the bomb.
When the bomb is released, the time taken by the bomb to reach the ground is t.
The distance travelled by the bomb and the plane will be u cos θt.
Hence, again the bomb will explode vertically below the plane.
(i)
During the motion of bomb, its horizontal velocity u remains constant and is the same as that of the plane at every point of its path.
Let the bomb reach the ground in time t.
Distance travelled in horizontal direction by the bomb = ut
Distance travelled in horizontal direction by the bomb is the same as that travelled by the plane.
So, the bomb will explode vertically below the plane.
(ii)
Let the plane move making an angle α with the horizontal.
Horizontal distance for both the bomb and the plane = u cos αt’
t’ = Time taken by the bomb to reach the ground
So, in this case also, the bomb will explode vertically below the plane.
Question 41:
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s2 and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
Answer-41
Acceleration of the car = 1 m/s2
Projection velocity of the ball (considered as a projectile) in the vertical direction = 9.8 m/s
Angle of projection, α = 90˚
Let u be the initial velocity of the car when the ball is thrown.
Both the car and the ball have the same horizontal velocity.
We know that the distance travelled by the ball in horizontal direction is given by -s = ut
Here, t is the time.
Also, the distance travelled by the car in horizontal direction is given by

Therefore, the ball drops 2 m behind the boy.
Question 42:
A staircase contains three steps each 10 cm high and 20 cm wide (figure 3−E9). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane?
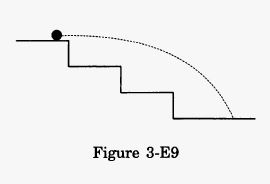
Answer-42
Height of one step = 10 cm
Width of one step = 20 cm
Total height of the staircase = y = 30 cm
Total width of the staircase = x = 40 cm
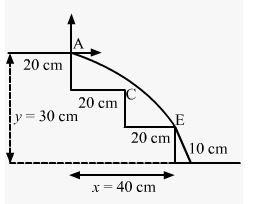
To directly hit the lowest plane, the ball should just touch point E.
Let point A be the origin of reference coordinate.
Let u be the minimum speed of the ball.
We have:
x = 40 cm
y = −20 cm
θ = 0°
g = 10 m/s2 = 1000 cm/s2
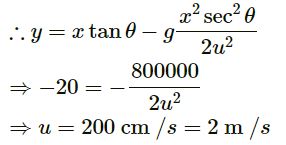
Question 43:
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection
(a) as seen from the truck,
(b) as seen from the road.
Answer-43
a) as seen from the truck,
Velocity of the truck = 14.7 m/s
Distance covered by the truck when the ball returns again to the truck = 58.8 m
Therefore, we can say that the time taken by the truck to cover 58.8 m distance is equal to the time of the flight of the truck.
Time in which the truck has moved the distance of 58.8 m:
T = 4 s
Time taken to reach the maximum height when the final velocity v = 0:
∴ v = u − at
⇒ 0 = u + 9.8 × 2
⇒ u = 19.6 m/s
19.6 m/s is the initial velocity with which the ball is thrown upwards
(b) as seen from the road.
Velocity of the truck = 14.7 m/s
Distance covered by the truck when the ball returns again to the truck = 58.8 m
From the road, the motion of ball seems to be a projectile motion.
Total time of flight (T) = 4 seconds
Horizontal range covered by the ball in this time, R = 58.8 m
We know:
R = u cos αt
Here, α is the angle of projection.
Now,
u cos α = 14.7 …(i)
Now, take the vertical component of velocity.
Using the equation of motion, we get:

u= 14.7 /cos 53
= 24.42 m/s
=25 m/s (appr)
Therefore, when seen from the road, the speed of the ball is 25 m/s and the angle of projection is 53° with horizontal.
Question 44:
The benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one metre above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 53° with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
Answer-44
Angle of projection of the ball, α = 53°
Width and height of the bench = 1 m
Initial speed of the ball = 35 m/s
Distance of the first bench from the batsman = 110 m
The batsman strikes the ball 1 m above the ground.
Let the ball land on the nth bench.
∴ y = (n − 1) …(i)
And,
x = 110 + n – 1 = 110 + y
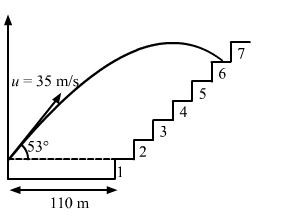
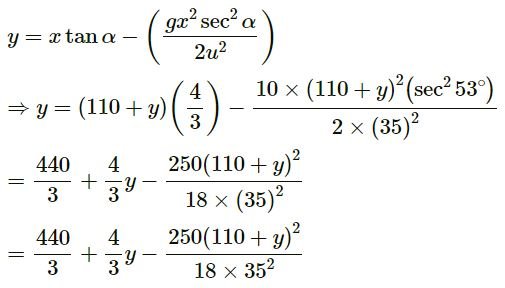
After Solving the equation, we will get:
y = 5
⇒ n − 1 = 5
⇒ n = 5 + 1
⇒ n = 6
Hence , The ball will hit the sixth bench of the gallery.
Question-45
A man is sitting on the shore of a river. He is in the line of 1.0 m long boat and is 5.5 m away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level.
Answer-45
Length of the boat = 1.0 m
Distance between the man and the centre of the boat (R) = 5.5 m
Initial speed (u) of throwing the apple by the man = 10 m/s
Acceleration due to gravity (g) = 10 m/s2
We know that the horizontal range is given by
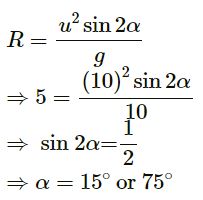
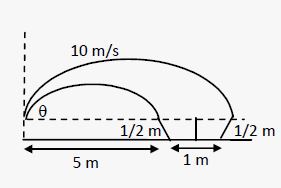
Similarly, for the end point of the boat, i.e., point C, we have:
Horizontal range (R) = 6 m
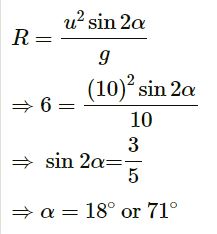
For a successful shot, the angle of projection α with initial speed 10 m/s may vary from 15° to 18° or from 71° to 75°. The minimum angle is 15° and the maximum angle is 75°, but there is an interval of 53° for which the successful shot is not allowed. We can show this by putting the successive value of α from 15° to 75°
HC Verma Concept of Physics Ch-3 Rest and Motions Exercise Questions Solutions
(Page No-54)
Question 46:
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?
Answer-46
Distance between the opposite shore of the river or width of the river = 400 m
Rate of flow of the river = 2.0 m/s
Boat is sailing at the rate of 10 m/s.
The vertical component of velocity 10 m/s takes the boat to the opposite shore. The boat sails at the resultant velocity vr.
Time taken by the boat to reach the opposite shore:
Time = Distance / Time
= 400 / 10
= 40s

(a)

Distance the boat need to travel to reach the opposite shore
= 400 / sin(α)
= 407.9 m
Time= Total Distance / Total Velocity
T = 407.9 / 10.2
T = 40s
(b)
Note – from part (a) of Q-46

Question 47:
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h.
(a) If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
(b) Find the shortest possible time to cross the river.
Answer-47
(a)
If he heads in a direction making an angle θ with the flow,
Width of the river = 500 m
Rate of flow of the river = 5 km/h
Swimmer’s speed with respect to water = 3 km/h
As per the question, the swimmer heads in a direction making an angle θ with the flow.
We know that the vertical component of velocity 3 sin θ takes him to the opposite side of the river.
Distance to be travelled = 0.5 km

Vertical component of velocity = 3 sin θ km/h
Thus, we have:
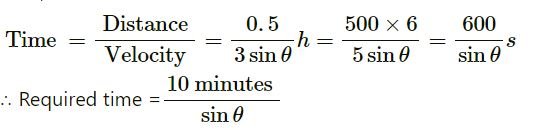
(b)
Shortest possible time to cover the river:
Take θ = 90∘
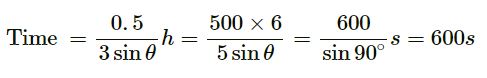
Hence, the required time is 10 minutes.
Question 48:
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
Answer-48
Width of the river = 500 m
Rate of flow of the river = 5 km/h
Swimmer’s speed with respect to water = 3 km/h
As per the question, the man has to reach the other shore at the point directly opposite to his starting point.
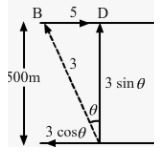
Horizontal distance is BD for the resultant velocity vr.
x-component of the resultant velocity, R = 5 – 3 cos θ
Vertical component of velocity = 3 sin θ km/h
Time = Distance / Velocity
=0.5 h / 3 sinθ
This is the same as the horizontal component of velocity.
Thus, we have:

= 16 / 24
= 2 / 3 km
Question 49:
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s.
(a) Find the direction in which the pilot should head the plane to reach the point B.
(b) Find the time taken by the plane to go from A to B.
Answer-49
(a)
Distance between points A and B = 500 km
B from A is 30˚ east of north.
Speed of wind due north, vw = 20 m/s
Airspeed of the plane, va = 150 m/s
Let R be the resultant direction of the plane to reach point B.

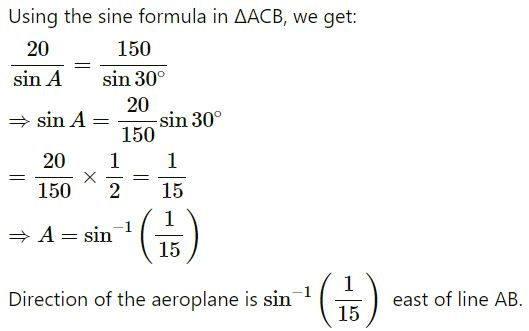
(b)
from part (a) of Q-49

Question 50:
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
Answer-50
Distance between A and B = x
Velocity of sound in air = v
Velocity of wind = u
First Case:
When A beats the drum from his original position:
Resultant velocity of sound = u + v

from (i) we get
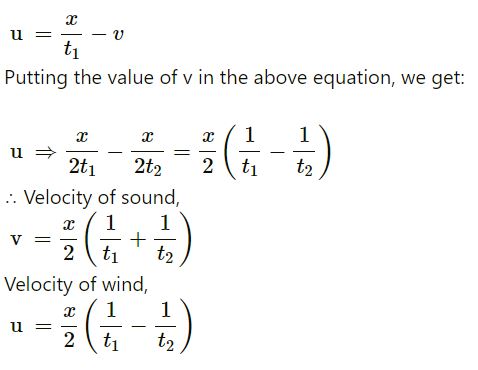
Question 51:
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
Answer-51
Distance between A and B = x
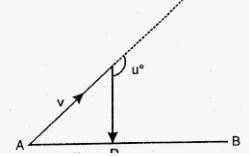
Let v be the velocity of sound in the direction along line AC.
Let u be the velocity of air in the direction along line AB.
Angle between v and u = θ > π / 2
Resultant velocity of sound and air that will reach B =

Question 52:
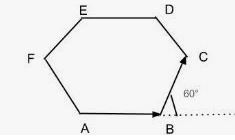
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
Answer-52
A regular hexagon has a side a. Six particles situated at the corners of the hexagon are moving with a constant speed v.
As per the question, each particle maintains a direction towards the particle at the next corner. So, particles will meet at centroid O of triangle PQR. Now, at any instant, the particles will form an equilateral triangle PQR with the same centroid O.
We know that P approaches Q, Q approaches R and so on.
Now, we will consider the motion of particle P. Its velocity makes an angle of 60˚.
This component is the rate of decrease of distance PO.
Relative velocity between P and Q:

—: End of Rest and Motions Exercise Questions Solutions HC Verma Vol-I :–
Thanks



Car question may be solve by this https://www.updateans.com/2019/07/a-car-travelling-at-60-kmh-overtakes.html
visit contact us and call to relevant subject teacher