Rotational Motion and Angular Momentum Numerical Class-11 Nootan ISC Physics Solutions Ch-11. Step by step Solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.

Rotational Motion and Angular Momentum Numerical Class-11 Nootan ISC Physics Solutions
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Writer | Kumar and Mittal |
| Publication | Nageen Prakashan |
| Chapter-11 | Rotational Motion of a rigid body: Moment of Inertia |
| Topics | Numericals on Torque, Equations of Rotational Motion and Angular Momentum |
| Academic Session | 2024-2025 |
Numericals on Torque, Equations of Rotational Motion and Angular Momentum
Ch-11 Rotational Motion of a rigid body: Moment of Inertia class-11 Nootan ISC Solutions of Kumar and Mittal Physics Nageen Prakashan
Q-1: A grindstone starts from rest and has a constant angular acceleration of 3.0 rad/s. Find: (i) the angular displacement, (ii) the angular speed, after 2.0 second.
Ans- given α = 3 rad/s , t= 2 s , θ = ? , ω = ? , ωo = 0
According to formula,
(i) θ = ωo t + 1/2 α t²
=> 0 + 1/2 x 3 x 2²
=> 6 rad
again,
(ii) ω = ωo + α t
=> 0 + 3 x 2
=> 6 rad/s
Q-2: The angular velocity of a wheel increases from 1200 to 4500 revolutions per minute in 10 second. Find its (i) angular acceleration, (ii) number of revolutions made during this time.
Ans- No = 1200 / min , N = 4500 / min , t = 10 s
α = ?
No = 1200 / 60 = 20
ωo => 2 π x 20 = 40 π rad /s
N = 4500 / 60 = 75
ω => 2 π x 75 = 150 π rad /s
(i) α = (ω – ωo) / t
=> (150 π – 40 π) / 10
=> 11 π rad/s²
and θ = [(ω – ωo) / 2] * t
=> [(150 π – 40 π) / 2] * 10
=> 190 π rad /s
(ii) no. of revolutions = 190 π x 5 / 2 π
=> 95 x 5
=> 475
Q-3: A constant torque turns a wheel through an angle of 40 radian in 2 second starting from rest. What is the angular acceleration? If the same torque continues then what will be angular velocity after 10 second from start?
Ans- Given,
ωo = 0 , θ = 40 rad , t = 2 s , α = ?
and ω after 10 s
According to formula θ = ωo t + 1/2 α t²
=> 40 = 0 + 1/2 x α x 2 ²
Hence α = 20 rad / s²
again ω = ωo + α t
=> ω = 0 + 20 x 10
=> 200 rad /s
Q-4: A sphere of mass 25 kg and diameter 0.4 m is revolving about its geometrical axis at the rate of 2100 revolutions per min. Calculate its: (i) moment of inertia, (ii) angular momentum.
Ans- M = 25 kg
R = 0.4/2 = 0.2 m
N = 2100 => n = 2100/60 = 35
I = ? , L = ?
(i) I = 2/5 MR²
=> 2/5 x 25 x (0.2)²
=> 10 x 0.04
Hence 0.4 kg-m²
(ii) L = I ω
=> I x 2 π n
=> 0.4 x 2 x 22/7 x 35
Hence 88 kg-m²/s
Q-5: Calculate the angular momentum of a disc whose rotational K.E. is 10 kJ and moment of inertia about its axis is 4.5 x 10^4 kg-m².
Ans- Relation between kinetic Energy and angular momentum
=> K = L² / 2 I
=> 10 x 10³ = L ² / (2 x 4.5 x 10^-4)
Hence L² = 9, L = 3.0 kg-m²/s
Q-6: A disc has moment of inertia of 0.5 kg-m². Find the work done to increase its speed from 3 rps to 8 rps.
Ans- Work done = change in energy
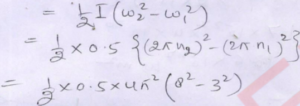
=> π² (64 – 9), = 55 π²
=> 55 x (3.14)²
Hence 542.3 J
Q-7: The moment of inertia of a ring is 0.40 kg-m². If it is rotating at a rate of 2100 revolutions per minute, calculate the torque required to stop it in 2.0 seconds. What will be the work done?
Ans- I = 0.4 kg-m²
n = 2100/60 = 35
ωo = 2 π n = 2 x 22/7 x 35 = 220 rad/s
now, ω = ωo + α t
α = ω – ωo / t
=> 220 – 0 /2 = 110
now τ = I α
=> 0.4 x 110
=> 44 N-m
again work done = K.E
=> 1/2 x 0.4 x (220)²
=> 9680 J
—: end of Rotational Motion and Angular Momentum Numerical Class-11 Nootan ISC Solutions Ch-11 :—
Return to : – Nootan Solutions for ISC Physics Class-11 Nageen Prakashan
Thanks
Please Share with your friends if helpful


