Sets Class- 7th RS Aggarwal Exe-6 D Goyal Brothers ICSE Maths Solution . We provide step by step Solutions of lesson-6 Sets for ICSE Class-7 Foundation RS Aggarwal Mathematics of Goyal Brothers Prakashan . Our Solutions contain all type Questions of Exe-6 D to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7 Mathematics. we would learn in this article about Cardinal properties of sets . What is cardinal of a set with an example? What is the cardinal number of set? What are cardinal formula sets?
Sets Class- 7th RS Aggarwal Exe-6 D Goyal Brothers ICSE Maths Solution
| Board | ICSE |
| Publications | Goyal brothers Prakashan |
| Subject | Maths |
| Class | 7th |
| Chapter-6 | Sets |
| Writer | RS Aggrawal |
| Book Name | Foundation |
| Topics | Solution of Exe-6 D |
| Academic Session | 2023 – 2024 |
What is Cardinal properties of sets
The word cardinal numbers or cardinal was coined to express the cardinality (size) of sets, which is the size of a set. The number of elements in a finite set is called cardinality, and it is used to characterize the size of the sets.
What is cardinal of a set with an example?
The cardinality of a set is defined as the number of elements in a mathematical set. It can be finite or infinite. For example, the cardinality of the set A = {1, 2, 3, 4, 5, 6} is equal to 6 because set A has six elements.
What are cardinal formula sets?
The cardinal number of a set A is denoted as n(A), where A is any set and n(A) is the number of members in set A. Consider a set A consisting of the prime numbers less than 10. Set A ={2, 3, 5, 7}. As the set A consists of 4 elements, therefore, the cardinal number of set A is given as n(A) = 4.
Exercise – 6 D
Sets Class- 7th RS Aggarwal Goyal Brothers ICSE Maths Solution
1. Let A and B be two sets such that n(A) = 52, n(B) = 60 and n(A ∩B) = 16. Draw a venn diagram and find : (i) n(A ∪ B) (ii) n(A – B) (iii) n(B – A).
Solution: (i) n(A ∪ B)
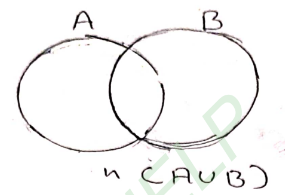
n(A) = 52, n(B) = 60 and n(A ∩B) = 16
But n(A ∪ B) = n(A) + n(B) – n(A ∩B)
n(A ∪ B) = 52 + 60 – 16
n(A ∪ B) = 112 – 16
n(A ∪ B) = 96
Solution: (ii) n(A – B)

n(A – B) = n(A) – n(A ∩B)
n(A – B) = 52 – 16
n(A – B) = 36
Solution: (iii) n(B – A)
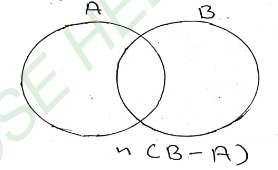
n(B – A) = n(B) – n(A ∩B)
n(B – A) = 60 – 16
n(B – A) = 44
2. Let P and Q be two sets such that n(P ∪ Q) = 70, n(P) = 45 and n(Q) = 38. Draw a venn diagram and find : (i) n(P ∩ Q) (ii) n(P – Q) (iii) n(Q – P).
Solution: (i) n(P ∩ Q)

n(P ∪ Q) = n(P) + n(Q) – n(P ∩ Q)
70 = 45 + 38 – n(P ∩ Q)
70 = 83 – n(P ∩ Q)
n(P ∩ Q) = 83 – 70
n(P ∩ Q) = 13
Solution: (ii) n(P – Q)
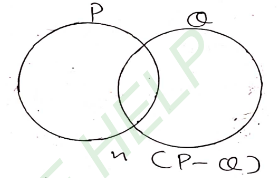
n(P – Q) = n(P) – n(P ∩ Q)
n(P – Q) = 45 – 13
n(P – Q) = 32
Solution: (iii) n(Q – P)

n(Q – P) = n(Q) – n(P ∩ Q)
n(Q – P) = 38 – 13
n(Q – P) = 25
3. In a city, there are 25 Hindi medium schools, 18 English medium schools and 7 schools have both the mediums. Find
(i) how many school are there in all in the city ;
(ii) how many school have Hindi medium only ;
(iii) how many school have English medium only.
Solution: Let H be the set of Hindi medium school, E be the set of English medium school.
(i) There in all in the city ;
∴ n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
n(H ∪ E) = 25 + 18 – 7
n(H ∪ E) = 43 – 7
n(H ∪ E) = 36
(ii) Only Hindi medium schools ;
∴ n(H ∪ E) = n(H) – n(H ∩ E)
n(H ∪ E) = 25 – 7
n(H ∪ E) = 18
(iii) Only English medium schools
∴ n(H ∪ E) = n(E) – n(H ∩ E)
n(H ∪ E) = 18 – 7
n(H ∪ E) = 11
4. There is a group of 50 persons who can speak English or Tamil or both. Out of these persons, 37 can speak English and 30 can speak Tamil.
(i) How many can speak both English and Tamil?
(ii) How many can speak English only?
(iii) How many can speak Tamil only?
Solution: No. of person who can speak English or Tamil or both n(E ∪ T) = 50
No. of person who can speak English n(E) = 37
No. of person who can speak Tamil n(T) = 30
Let E be the set of person speaking English and T be the set of person speaking Tamil
∴ n(E ∪ T) = 50
n(E) = 37
n(T) = 30
(i) No. of person who can speak English or Tamil
n(E ∪ T) = n(E) + n(T) – n(E ∩ T)
50 = 37 + 30 – n(E ∩ T)
50 = 67 – n(E ∩ T)
n(E ∩ T) = 67 – 50
n(E ∩ T) = 17
(ii) No. of person who can speak English only
n(E ∪ T) = n(E) – n(E ∩ T)
n(E ∪ T) = 37 – 17
n(E ∪ T) = 20
(iii) No. of person who can speak Tamil only
n(E ∪ T) = n(T) – n(E ∩ T)
n(E ∪ T) = 30 – 17
n(E ∪ T) = 13
5. In a class of 40 students, each one plays either Tennis or Badminton or both. If 28 play Tennis and 26 play Badminton, find
(i) how many play both the games;
(ii) how many play Tennis only;
(iii) how many play Badminton only.
Solution: No. of student who can play either Tennis or Badminton or both n(T ∪ B) = 40
No. of student who can play Tennis n(T) = 18
No. of student who can play Badminton n(B) = 26
T be the set of student who can play Badminton
∴ n(T ∪ B) = 40
n(T) = 18
n(B) = 26
(i) No. of student who can play either Tennis or Badminton or both
n(T ∪ B) = n(T) + n(B) – n(T ∩ B)
40 = 28 + 26 – n(T ∩ B)
40 = 54 – n(T ∩ B)
n(T ∩ B) = 54 – 40
n(T ∩ B) = 14
(ii) No. of student who can play Tennis only
n(T ∪ B) = n(T) – n(T ∩ B)
n(T ∪ B) = 28 – 14
n(T ∪ B) = 14
(iii) No. of student who can play Badminton only
n(T ∪ B) = n(B) – n(T ∩ B)
n(T ∪ B) = 26 – 14
n(T ∪ B) = 12
6. In a class of 45 pupils, 21 play chess, 23 play cards and 5 play both the games. Find
(i) how many do not play any of the games;
(ii) how many play chess only;
(iii) how many play cards only.
Solution: Let C be the set of pupils playing chess and K playing cards
Total number of pupils = 45
No. of pupils who can play chess n(C) = 21
No. of pupils who can play cards n(K) = 23
(i) No. of pupils who can play chess or cards or both
∴ n(C ∪ K) = n(C) + n(K) – n(C ∩ K)
n(C ∪ K) = 21 + 23 – 45
n(C ∪ K) = 44 – 45
n(C ∪ K) = 1
5 play both the games
5 + 1 = 6
(ii) No. of pupils who can play chess
n(C ∪ K) = n(C) – n(C ∩ K)
n(C ∪ K) = 21 – 5
n(C ∪ K) = 16
(iii) No. of pupils who can play cards
n(C ∪ K) = n(K) – n(C ∩ K)
n(C ∪ K) = 23 – 5
n(C ∪ K) = 18
7. In a group of 36 girls, each one can either stitch or weave or can do both. If 25 girls can stitch and 17 can stitch only, how many can weave only?
Solution: No. of girls who can either stitch or weave or both = 36
No. of girls who can stitch = 25
No. of girls who can stitch only = 17
Let S be the set of girls who can stitch and W be the set of girls who can weave
∴ n(S ∪ W) = 36
n(S) = 25
No. of girls who can stitch only = 17
No. of girls who can weave only = 36 – 25
No. of girls who can weave only = 11
8. In a group of 24 children, each on plays cricket or hockey or both. If 16 play cricket and 12 play cricket only, find how many play hockey only.
[Hint. n(C ∪ H) = 24, n(C) = 16, n(C – H) = 12]
Solution: Total number of children = 24
Let C be the set of children playing cricket and H be the set of children playing hockey
∴ n(C ∪ H) = 24
n(C) = 16
n(C – H) = 12
n(C) – n(C ∩ H) = n(C – H)
16 – n(C ∩ H) = 12
n(C ∩ H) = 16 -12
n(C ∩ H) = 4
∴ No. of children who can play hockey only = 24 – 16
No. of children who can play hockey only = 8
9. In a group of 40 persons, 10 drink tea but not coffee and 26 drink tea. How many drink coffee but not tea?
Solution: Total number of persons = 40
people who can drink only tea but not coffee = 10
people who can drink only tea = 26
Let T be the set of drinking tea and C be the set of drinking coffee
∴ n(T ∪ C) = 40
n(T) = 26
n(T ∩ C) = 10
∴ No. of person drinking coffee not tea = 40 – 26
No. of person drinking coffee not tea = 14
10. All the people in a locality read the daily newspaper Indian Express or Hindustan Times or both. If 120 read Indian Express and 150 read Hindustan Times and 36 read both, find :
(i) How many people are there in the locality;
(ii) How many people read only Indian Express.
Solution: No. of people who read Indian Express = 120
No. of people who read Hindustan Times = 150
No. of people who read both = 36
Let I be the set of people reading Indian Express and H be the set of people reading Hindustan Times
Then, n(I) = 120
n(I ∩ H) = 36
(i) No. of people in the locality
n(I ∪ H) = n(I) + n(H) – n(I ∩ H)
n(I ∪ H) = 120 + 150 – 36
n(I ∪ H) = 270 – 36
n(I ∪ H) = 234
∴ No. of people in the locality = 234
(ii) No. of people who read only Indian Express
n(I ∪ H) = n(I) – n(I ∩ H)
n(I ∪ H) = 120 – 36
n(I ∪ H) = 84
— : end of Sets Class- 7th RS Aggarwal Exe-6 D Goyal Brothers ICSE Maths Solution:–
Return to- ICSE Class -7 RS Aggarwal Goyal Brothers Math Solutions
Thanks
Please share with yours friends if you find it helpful.


