Study of Gas Laws Exe-7 MCQs Answer Chemistry Class-9 ICSE Selina Publishers
Concise Selina Publishers Chemistry ICSE Class-9 Chapter-7 Study of Gas Laws Numercal Based on Boyel's Law and Numercal Based on Charles' Law .
Study of Gas Laws Exe-7 MCQs Answer Chemistry Class-9 ICSE Selina Publishers Solutions Chapter-7. Step By Step ICSE Selina Concise Solutions of Chapter-7 Study of Gas Laws with All Exercise including MCQs, Very Short Answer Type, Short Answer Type, Long Answer Type, Numerical and Structured/Application Questions Solved . Visit official Website CISCE for detail information about ICSE Board Class-9.
Study of Gas Laws Exe-7 MCQs Answer Chemistry Class-9 ICSE Concise Selina Publishers
| Board | ICSE |
| Publications | Selina Publication |
| Subject | Chemistry |
| Class | 9th |
| Chapter-7 | Study of Gas Laws |
| Book Name | Concise |
| Topics | Solution of Exercise – 7 MCQs Answer Type |
| Academic Session | 2023-2024 |
A. Exercise – 7 MCQs Answer Type
Study of Gas Laws Class-9 Chemistry Concise Solutions
Page-131
(Choose the correct answer from the option given below).
1. The graph of PV vs P for a gas is :
(i) parabolic
(ii) hyperbolic
(iii) a straight line parallel to X-axis
(iv) a straight line passing through origin
Answer:
(iii) a straight line parallel to X-axis
2. The absolute temperature value that corresponds to 27°C is :
(i) 200 K
(ii) 300 K
(iii) 400 K
(iv) 246 K
Answer:
(ii) 300 K
3. Volume-temperature relationship is given by :
(i) Boyle
(ii) Gay Lussac
(iii) Dalton
(iv) Charles
Answer:
(iv) Charles
4. If pressure is doubled for a fixed mass of a gas, its volume will become :
(i) 4 times
(ii) 1⁄2 times
(iii) 2 times
(iv) No change
Answer:
(ii) 1⁄2 times
5. The S.I. unit of temperature is :
(i) Pascal
(ii) °C
(iii) Kelvin
(iv) °F
Answer:
(iii) Kelvin
6. Which of the following temperatures is known as the steam point ?
(i) 273 K
(ii) 373 K
(iii) 290 K
(iv) 273°C
Answer:
(ii) 373 K
7. The graph shown below gives the statement for :
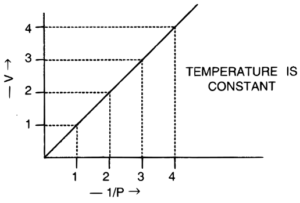
(i) Henry’s law
(ii) Charles’ law
(iii) Boyle’s law
(iv) Daltons’ law
Answer:
(iii) Boyle’s law
8. ‘The volume of a given amount of a gas is directly proportional to its absolute temperature at a constant pressure’ is the statement of :
(i) Gay-Lussac’s law
(ii) Boyle’s law
(iii) Charles’ law
(iv) Mendeleev’s law
Answer:
(iii) Charles’ law
9. The volume of a given mass of a gas at constant temperature and 10 atmospheric pressure is 10 litres. Its volume at 5 atmospheres will be :
(i) 5 litres
(ii) 10 litres
(iii) 15 litres
(iv) 20 litres
Answer:
(iv) 20 litres
10. STP is called standard temperature and pressure. The standard temperature and standard pressure respectively are :
(i) 273 K and 760 mm
(ii) 0°C and 760 cm
(iii) 273°C and 1 atmosphere
(iv) 373 K and 76 cm
Answer:
(iii) 273 K and 760 mm
— : End of Study of Gas Laws Exe-7 MCQs Answer Class-9 ICSE Chemistry Solutions :–
Return to Return to Concise Selina ICSE Chemistry Class-9
Thanks
Please share with your friends
