Triangles ICSE Class-7th Concise Selina Mathematics Solutions Chapter-15 . We provide step by step Solutions of Exercise / lesson-15 Triangles for ICSE Class-7 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-15 A , Exe-15 B, and Exe-15 C to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7.
Triangles ICSE Class-7th Concise Selina Mathematics Solutions Chapter-15
–: Select Topics :–
Exercise – 15 A Triangles ICSE Class-7th Concise Selina Mathematics Solutions
Question 1.
Stale, if the triangles are possible with the following angles :
(i) 20°, 70° and 90°
(ii) 40°, 130° and 20°
(iii) 60°, 60° and 50°
(iv) 125°, 40° and 15°
Answer
(i)
We know that,
the sum of three angles of a triangle is 180°,
therefore,
Sum of 20°, 70°, and 90°
= 20° + 70° + 90°
= 180°
Since the sum is 180°.
Hence it is possible.
(ii)
We know that,
the sum of three angles of a triangle is 180°,
therefore,
Sum of 40°, 130°, and 20°
= 40° + 130° + 20°
= 190°
Since the sum is not 180°,
Hence, it is not possible.
(iii)
We know that,
the sum of three angles of a triangle is 180°,
therefore,
Sum of 60°, 60°, and 50°
= 60° + 60° + 50°
= 170°
Since the sum is not 180°,
Hence, it is not possible.
(iv)
We know that,
the sum of three angles of a triangle is 180°,
therefore,
Sum of 125°, 40°, and 15°
= 125° + 40° + 15°
= 180°
Since the sum is 180°,
Hence, it is possible.
Question 2.
If the angles of a triangle are equal, find its angles.
Answer
Since the three angles of a triangle are equal and their sum is 180°, therefore each angle will be
180°/3=60°.
Question 3.
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
Answer
Since the sum of angles of a triangle is 180°
so ∠A + ∠B + ∠C = 180°
⇒ 45° + 75° + ∠C = 180°
⇒ 120° + ∠C
= 180°
⇒ ∠C = 180° − 120°
= 60°
Question 4.
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Answer
∠Q = ∠R = x, ∠P
= 60°
But ∠P + ∠Q + ∠R
= 180°
∴ 60° + x + x = 180°
⇒ 60° + 2x = 180°
⇒ 2x = 180° − 60° =
120°
⇒ x =120°/2
=60°
∴ ∠Q = ∠R = 60°
Hence,
∠R = 60°
Question 5.
Calculate the unknown marked angles in each figure :

Answer
(i)
We know that,
the sum of three angles of a triangle is 180°,
therefore,
From figure,
90° + 30° + x = 180°
⇒ 120° + x = 180°
⇒ x = 180° − 120°
= 60°
Hence,
x = 60°
(ii)
We know that,
the sum of three angles of a triangle is 180°,
therefore,
From figure,
y + 80° + 20° = 180°
⇒ y + 100° = 180°
⇒ y = 180° − 100° = 80°
Hence,
y = 80°
(iii)
We know that,
the sum of three angles of a triangle is 180°,
therefore,
In figure,
a + 90° + 40°
= 180°
⇒ a + 130° = 180°
⇒ a = 180° − 130°
= 50°
Hence,
a = 50°
Question 6.
Find the value of each angle in the given figures:

Answer
(i)
From the figure,
∠A + ∠B + ∠C = 180° …..(Sum of angles of a triangle)
⇒ 5x° + 4x° + x° = 180°
⇒ 10x° = 180°
⇒ x = 180°/10
=18°
∴ ∠A = 5x° = 5× 18°
= 90°
∠B = 4x = 4 × 18°
= 72°
and ∠C = x = 18°
(ii)
From the figure,
∠A + ∠B + ∠C = 180° …..(Sum of angles of a triangle)
⇒ x° + 2x° + 2x° = 180°
⇒ 5x° = 180°
⇒ x° = 180°/5
=36°
∴ ∠A = x° = 36°
∠B = 2x° = 2 × 36°
= 72°
and ∠C = 2x° = 2 × 36°
= 72°
Question 7.
Find the unknown marked angles in the given figure:

Answer
(i)
From the figure,
∠A + ∠B + ∠C = 180° …..(Sum of angles of a triangle)
b° + 50° + b° = 180°
⇒ 2b° + 50° = 180°
⇒ 2b° = 180° − 50°
= 130°
⇒ b° = 130°/2=65°
Hence,
∠A = b° =
65°
∠C = b°
= 65°
(ii)
From the figure,
∠A + ∠B + ∠C = 180° …..(Sum of angles of a triangle)
x° + 90° + x° = 180°
⇒ 2x°+ 90°
= 180°
⇒ 2x° = 180° − 90°
⇒ 2x°= 90°
⇒ x° = 90°/2
=45°
Hence,
∠A = x° = 45°
∠C = x° = 45°
(iii)
From the figure,
∠A + ∠B + ∠C = 180° …..(Sum of angles of a triangle)
k°+ k°+ k°= 180°
⇒ 3k° = 180°
⇒ k° =180°/3
=60°
Hence,
∠A = k° = 60°,
∠B = k° = 60°
∠C = k° = 60°
(iv)
Question 8.
In the given figure, show that: ∠a = ∠b + ∠c

(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
Answer
if AB || CD
so b = c and ∠A = ∠C ……..(Alternate angles)
Now in Δ PCD,
Ext. ∠APC = ∠C + ∠D
⇒ a = b + c
(i) If b = 60°, c = 50°, then
a = b + c = 60° + 50°
= 110°
(ii) If a = 100° and b = 55°,
then a = b + c
⇒ 100° = 55°+ c
⇒ c = 100°− 55°
= 45°
(iii) If a = 108° and c = 48°
then a = b + c
⇒ 108° = b + 48°
⇒ b = 108°− 48°
= 60°
Question 9.
Calculate the angles of a triangle if they are in the ratio 4 : 5 : 6.
Answer
We know that,
sum of angles of a triangle is 180°
so ∠A + ∠B + ∠C = 180°
But ∠A: ∠B: ∠C = 4: 5: 6
∠A = 4x, ∠B = 5x and ∠C = 6x,
then
4x + 5x + 6x = 180°
⇒ 15x = 180°
⇒ x = 180°/15
=12°
∴ ∠A = 4x = 4 × 12°
= 48°
∠B = 5x = 5 × 12° =
60°
∠C = 6x = 6 × 12°
= 72
Question 10.
One angle of a triangle is 60°. The, other two angles are in the ratio of 5 : 7. Find the two angles.
Answer
In Δ ABC,
∠A = 60° and
then
∠B: ∠C = 5: 7
But ∠A + ∠B + ∠C = 180° ……..(Angles of a triangle)
⇒ 60° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 180°− 60°
= 120°
Let ∠B = 5x
and ∠C = 7x
∴ 5x + 7x = 120°
⇒ 12x = 120°
⇒ x =120°/12
=10°
∴ ∠B = 5x = 5 × 10° = 50°
∠C = 7x = 7 × 10°
= 70°
Question 11.
One angle of a triangle is 61° and the other two angles are in the ratio 1 : 1
. Find these angles.
Answer
In Δ ABC,
∠A = 61°
But ∠A + ∠B + ∠C = 180° ……..(Angles of a triangle)

⇒ 61° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 180°− 61°
= 119°
But ∠B: ∠C =1 (1/2) : 1 (1/3) = (3/2) : (4/3)
=(9:8)/6
=9: 8
∠B = 9x
and ∠C = 8x,
then, 9x + 8x = 119°
⇒ 17x = 119°
⇒ x =119°17=7°
so ∠B = 9x = 9 × 7° = 63°
∠C = 8x = 8 × 7°
= 56°
Question 12.
Find the unknown marked angles in the given figures :

Answer
(i)
We know that,
in a triangle if one side of it is produced,
then
Exterior angle = sum of its interior opposite angles.
From the fig,
110° = x° + 30°
x° = 110°− 30°
= 80°
(ii)
We know that,
in a triangle if one side of it is produced,
then
Exterior angle = sum of its interior opposite angles.
From fig,
120° = y° + 60°
y° = 120°− 60°
= 60°
(iii)
We know that,
in a triangle if one side of it is produced,
then
Exterior angle = sum of its interior opposite angles.
From the fig,
122° = k° + 35°
⇒ k° = 122°− 35°
= 87°
(iv)
We know that,
in a triangle if one side of it is produced,
then
Exterior angle = sum of its interior opposite angles.
From the fig,
135° = a° + 73°
⇒ a° = 135°− 73°
= 62°
(v)
We know that/ in a triangle if one side of it is produced,
then
Exterior angle = sum of its interior opposite angles.
From the fig,
125° = a + c …….(i)
and 140° = a + b …………(ii)
Adding, we get
a + c + a + b = 125° + 140°
⇒ a + a + b + c = 265°
But a + b + c = 180° ……..(sum of angles of a triangle)
∴ a + 180° = 265°
⇒ a = 265° − 180° = 85°
But a + b = 140°
⇒ 85° + b = 140°
⇒ b = 140°− 85° = 55°
and a + c = 125°
⇒ 85° + c = 125°
⇒ c = 125° − 85° = 40°
Hence a = 85°,
b = 55°
c = 40°
(vi)
We know that,
in a triangle if one side of it is produced,
then
Exterior angle = sum of its interior opposite angles.
From the fig,
112° + x° = 180° ……………(Linear pair)
x = 180°− 112° = 68°
and 112° = y + 63° = 49°
Hence ,
x = 68°,
y = 49°
(vii)
We know that,
in a triangle if one side of it is produced,
then
Exterior angle = sum of its interior opposite angles.
From the fig,
120° + a + a
⇒ 2a = 120°
a =120°2
=60°
so a = 60°
(viii)
We know that,
in a triangle if one side of it is produced,
then
Exterior angle = sum of its interior opposite angles.
From the fig,
140° + a = 180° …..(Linear pair)
⇒ a = 180° − 140° = 40°
Now 4m = 2m = a
⇒ 4m − 2m = a
⇒ 2m = 40°
⇒ m = 40°/2=20°
hence,
m = 20°
(ix)
We know that,
in a triangle if one side of it is produced,
then
Exterior angle = sum of its interior opposite angles.
From the fig,
105° = b + b
2b = 105°
b =105°/2
=52.5°
But a + 105° = 180° ……..(Linear pair)
⇒ a = 180° − 105°
= 75°
Hence,
a = 75°,
b = 52.5°
Exercise – 15 B Triangles for ICSE Class-7th Concise Mathematics Selina Solutions
Question 1.
Find the unknown angles in the given figures:

Answer
(i)
From the fig,
x = y ………(Angles opposite to equal sides)
But x + y + 80° = 180° ………(Angles of a triangle)
⇒ x + x + 80° = 180°
⇒ 2x + 80° = 180°
⇒ 2x = 180°− 80°
= 100°
⇒ x = 100°/2
=50°
∴ y = x = 50°
Hence,
x = 50°,
y = 50°
(ii)
From the fig,
b = 40° ………(Angles opposite to equal sides)
But a + b + 40° = 180° ………(Angles of a triangle)
⇒ a + 40°+ 40° = 180°
⇒a + 80° = 180°
⇒ a = 180°− 80° = 100°
Hence,
a = 100°,
b = 40°
(iii)
From the fig,
x = y ………(Angles opposite to equal sides)
But x + y + 90° = 180° ………(Angles of a triangle)
⇒ x + x + 90° = 180°
⇒ 2x + 90° = 180°
⇒ 2x = 180°− 90° = 90°
∴ x =90°/2
=45°
∴ y = x = 45°
Hence,
x = 45°,
y = 45°
(iv)
From the fig,
a = b ………(Angles opposite to equal sides)
But a + b + 80° = 180° ………(Angles of a triangle)
⇒ a + a + 80° = 180°
⇒ 2a + 80° = 180°
⇒ 2a = 180°− 80°
= 100°
⇒ a =100°/2=50°
∴ b = a = 50°
x = a + 80° …….(Exterior angle of a triangle is equal to sum of its opposite interior angles)
= 50° + 80° = 130°
Hence,
a = 50°,
b = 50°
x = 130°
(v)
From the fig,
Let each equal angle of an isosceles triangle be x,
then x + x = 86° ⇒ 2x = 86°
⇒ x =86°/2=43°
But p + x = 180° ……….(Linear pair)
p + 43° = 180°
⇒ p = 180° − 43°
⇒ p = 137°
Hence,
p = 137°
(vi)
From the fig,
m = 35° ………(Angles opposite to equal sides)
But m + n + (60° + 35°) = 180° ……….(Angles of a triangle)
⇒ m + n + 95° = 180°
⇒ 35° + n + 95°
= 180°
⇒ n + 130° = 180°
⇒ n = 180° − 130°
= 50°
Hence,
m = 35°,
n = 50°
(vii)
From the fig,
x = 60° ………(Alternate angles)
Each equal angle of an isosceles triangle be a
then a + a + x = 180° ……….(Angles of a triangle)
⇒ 2a + x = 180°
⇒ 2a + 60° = 180°
⇒ 2a = 180° − 60° = 120°
⇒ a =120°/2
=60°
∴ y = x + a = 60°
= 120°
Hence,
x = 60°
y = 120°
Question 2.
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figures :

Answer
(i)
From the fig,
a = 70° ………..(Angles opposite to equal sides)
But a + 70° + x = 180° ………..(Angles of a triangle)
⇒ 70° + 70° + x = 180°
⇒ 140° + x = 180°
⇒ x = 180° − 140° = 40°
y = b ………(Angles opposite to equal sides)
But a = y + b ………..(Exterior angle of a triangle is equal to sum of its interior opposite angles)
⇒ 70° = y + y
⇒ 2y = 70°
⇒ y =70°/2
=35°
Hence,
x = 40°,
y = 35°
(ii)
From the fig,
In an equilateral triangle.
each angle = 60°
In an isosceles triangle.,
Let each base angle = a
∴ a + a + 100° = 180°
⇒ 2a + 100° = 180°
⇒ 2a = 180° − 100° = 80°
∴ a = 80°/2
=40°
∴ x = 60° + 40° = 100°
and y = 60° + 40° = 100°
(iii)
From the fig,
130° = x + p ……..(Exterior angle of a triangle is equal to the sum of its interior opposite angles)
∵ Lines are parallel ……..(Given)
∴ p = 60° …………..(Alternate angle)
and y = a
But a + 130° = 180° ……….(Linear pair)
⇒ a = 180° − 130° = 50°
∴ y = 50°
and x + p = 130°
⇒ x + 60° = 130°
⇒ x = 130° − 60° = 70°
Hence,
x = 70°,
y = 50°,
p = 60°
(iv)
From the fig,
x = a + b
But b = y ……….(Angles opposite to equal sides)
Similarly a = c
But a + c + 30° = 180°
⇒ a + a + 30° = 180°
⇒ 2a + 30° = 180°
⇒ 2a = 180° − 30° = 150°
⇒ a =150°/2=75°
and b + y = 90°
⇒ y + y = 90°
⇒ 2y = 90°
⇒ y =90°2=45°
⇒ b = 45°
Hence,
x = a + b = 75° + 45° = 120°
and y = 45°
(v)
From the fig,
a + b + 40° = 180° ……..(Angles of a triangle)
⇒ a + b = 180° − 40° = 140°
But a = b ……….(Angles opposite to equal sides)
∴ a = b =140°/2=70°
∴ x = b + 40° = 70° + 40° = 110° ………(Exterior angle of a triangle is equal to the sum of its interior opposite angles)
Similarly y = a + 40°
= 70° + 40° = 110°
Hence,
x = 110°,
y = 110°
(vi)
From the fig,
a = b ……….(Angles opposite to equal sides)
∴ y = 120°
But a + 120° = 180° …………..(Linear pair)
⇒ a = 180°− 120° = 60°
∴ b = 60°
But x + a + b = 180° ……………(Angles of a triangle)
⇒ x + 60° + 60° = 180°
⇒ x + 120° = 180°
∴ x = 180°− 120° = 60°
b = z + 25 ………(Exterior angle of a triangle is equal to the sum of its interior opposite angles)
⇒ 60° = z + 25°
⇒ z = 60°− 25°
= 35°
Hence,
x = 60°,
y = 120° ,
z = 35°
Question 3.
The angle of vertex of an isosceles triangle is 100°. Find its base angles.
Answer
In Δ ABC,
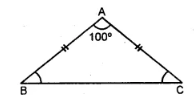
if AB = AC.
so ∠B = ∠C
But ∠A = 100°
and ∠A + ∠B + ∠C = 180° ……….(Angles of a triangle)
⇒ 100° + ∠B + ∠B
= 180°
⇒ 2 ∠B = 180°− 100°
⇒ 2 ∠B = 80°
∴ ∠B =80°/2=40°
Hence,
∠B = ∠C = 40°
Question 4.
One of the base angles of an isosceles triangle is 52°. Find its angle of vertex.
Answer
Each of the base angles of an isosceles
Δ ABC = 52°
∴ ∠B = ∠C = 52°
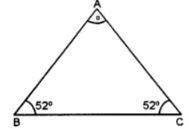
But ∠A + ∠B + ∠C = 180°……….(Angles of a triangle)
⇒ ∠A + 52° + 52°
= 180°
⇒ ∠A + 104° = 180°
⇒ ∠A = 180°− 104°
= 76°
Hence,
∠A = 76°
Question 5.
In an isosceles triangle, each base angle is four times of its vertical angle. Find all the angles of the triangle.
Answer
Vertical angle of an isosceles triangle = x
∴ Each base angle = 4x
∴ x + 4x + 4x = 180° …………(Sum of angles of a triangle)
⇒ 9x = 180°
⇒ x =180°/9
=20°
∴ Vertical angle = 20°
and each of the base angle = 4x
= 4 × 20° = 80°
Question 6.
The vertical angle of an isosceles triangle is 15° more than each of its base angles. Find each angle of the triangle.
Answer
Each angle of the base of the isosceles triangle = x°
Then vertical angle = x + 15°
Now x + x + x + 15° = 180° …………(Sum of angles of a triangle)
⇒ 3x + 15°= 180°
⇒ 3x = 180° − 15° = 165°
⇒ x =165°/3
=55°
Hence,
each base angle = 55°
and vertical angle = 55° + 15° = 70°
Question 7.
The base angle of an isosceles triangle is 15° more than its vertical angle. Find its each angle.
Answer
The vertical angle of the isosceles triangle = x°
∴ Each base angle = x + 15°
∴ x + 15° + x + 15° + x° = 180° …………(Sum of angles of a triangle)
⇒ 3x + 30°= 180°
⇒ 3x = 180° − 30° = 150°
∴ x =150°/3=50°
Hence,
vertical angle = 50°
and each base angle = 50° + 15° = 65°
Question 8.
The vertical angle of an isosceles triangle is three times the sum of its base angles. Find each angle.
Answer
Each base angle of an isosceles, triangle = x
then its vertical = 3 (x + x) = 3 × 2x = 6x.
∴ 6x + x + x = 180° ……….(Sum of angles of a triangle)
8x = 180°
x = 180°/8=22.5°
∴ Each base angle = 22.5°
and vertical angle = 3 × (22.5 + 22.5)
= 3 × 45 = 135°
Question 9.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1 : 4. Find each angle of the triangle.
Answer
Ratio between base angle and vertical angle of an isosceles triangle = 1: 4
each base angle = x
then vertical angle = 4x
∴ x + x + 4x = 180° ………(Sum of angles of a triangle)
6x = 180°
x =180°/6=30°
∴ Each base angle = x = 30°
and vertical angle = 4x
= 4 × 30° = 120°
Question 10.
In the given figure, BI is the bisector of∠ABC and Cl is the bisector of ∠ACB. Find ∠BIC.

Answer
In Δ ABC,
BI is the bisector of ∠ABC and CI is the bisector of ∠ACB.
∵ AB = AC
∴ ∠B = ∠C …………(Angles opposite to equal sides)
But ∠A = 40°
and ∠A + ∠B + ∠C = 180° ……(Angles of a triangle)
40° + ∠B + ∠B = 180°
40° + 2 ∠B = 180°
2 ∠B = 180° − 40° = 140°
∠B =140°/2
=70°
∴ ∠ABC = ∠ACB = 70°
But BI and CI are the bisectors of ∠ABC and ∠ACB respectively.
∴ ∠IBC =(1/2) ∠ABC =(1/2)(70°)=35°
and ∠ICB =(1/2) ∠ACB =(1/2)×70°=35°
Now in Δ IBC,
∠BIC + ∠IBC + ∠ICB = 180° ……..(Angles of a triangle)
⇒ ∠BIC + 35° + 35° = 180°
⇒ ∠BIC + 70° = 180°
⇒ ∠BIC = 180° − 70° = 110°
Hence,
∠BIC = 110°
Question 11.
In the given figure, express a in terms of b.

Answer
In Δ ABC,
BC = BA
∴ ∠BCA = ∠BAC
∠CBE = ∠BCA + ∠BAC
⇒ a = ∠BCA + ∠BCA
⇒ a = 2 ∠BCA ………(i)
But ∠ACB = 180° − b ……….(∵ ∠ACD and ∠ACB are linear pair)
⇒ ∠BCA = 180° − b ………….(ii)
∴ a = 2 ∠BCA = 2 (180° − b)
= 360°− 2b
Question 12.
(i)
(a) In Figure, BP bisects ∠ABC and AB = AC. Find x.
(b) Find x in Figure
(ii) Given: DA = DB = DC, BD bisects ∠ABC and ∠ADB = 70°.

Answer
(i)
From the figure,
AB = AC, and BP bisects ∠ABC
AP || BC is drawn.
Now ∠PBC = ∠PBA ………(∵ PB is the bisector of ∠ABC)
if AP || BC
so ∠APB = ∠PBC …………(Alternate angles)
x = ∠PBC ………………(i)
In Δ ABC, ∠A = 60°
and ∠B = ∠C ……………….(∵ AB = AC)
But ∠A + ∠B + ∠C = 180°…………………(Angles of a triangle)
⇒ 60° + ∠B + ∠C = 180°
⇒ 60° + ∠B + ∠B = 180°
⇒ 2 ∠B = 180° − 60° = 120°
∴ ∠B =120°/2=60°
⇒ (1/2)∠B=60°.2=30°
⇒ ∠PBC = 30°
∴ From (i),
x = 30°
(ii)
From the figure,
DA = DB = DC
BD bisects ∠ABC
and ∠ADB = 70°
But ∠ADB + ∠DAB + ∠DBA = 180° …………(Angles of a triangle)
⇒ 70° + ∠DBA + ∠DBA = 180° ……..(∵ DA = DB)
⇒ 70° + 2 ∠DBA = 180°
⇒ 2 ∠DBA = 180° − 70°
= 110°
∴ ∠DBA =110°/2=55°
if BD is the bisector of ∠ABC,
so ∠DBA = ∠DBC = 55°
But in Δ DBC,
DB = DC
∴ ∠DCB = ∠DBC
x = 55°
Question 13.
In each figure, given below, ABCD is a square and ∆ BEC is an equilateral triangle.
Find, in each case : (i) ∠ABE(ii) ∠BAE

Answer
(i)
We know that,
the sides of a square are equal
and each angle is of 90°
Three sides of an equilateral triangle are equal and each angle is of 60.
Therefore,
From fig,
ABCD is a square and Δ BEC is an equilateral triangle.
(i) ∠ABE = ∠ABC + ∠CBE
= 90° + 60° = 150°
(ii) But in Δ ABE
∠ABE + ∠BEA + ∠BAE = 180° ……………(Angles of a triangle)
⇒ 150° + ∠BAE + ∠BAE = 180° ………….(∵ AB = BE)
⇒ 150° + 2 ∠BAE = 180°
⇒ 2 ∠BAE = 180°− 150° = 30°
so ∠BAE =30°/2=15°
(ii)
We know that,
the sides of a square are equal and each angle is of 90°
Three sides of an equilateral triangle are equal and each angle is of 60.
From fig,
∴ ABCD is a square and Δ BEC is an equilateral triangle,
(i) ∠ABE = ∠ABC − ∠CBE
= 90° − 60° = 30°
(ii) In Δ ABE,
∠ABE + ∠AEB + ∠BAE = 180° ……………(Angles of a triangle)
⇒ 30° + ∠BAE + ∠BAE = 180° ………….(∵ AB = BE)
⇒ 30° + 2∠BAE = 180°
⇒ 2 ∠BAE = 180°− 30° = 150°
⇒ ∠BAE =150°/2
=75°
Question 14.
In ∆ ABC, BA and BC are produced. Find the angles a and h. if AB = BC.

Answer
In Δ ABC, sides BA and BC are produced
∠ABC = 54°;
AB = BC
Now in Δ ABC,
∠BAC + ∠BCA + ∠ABC = 180° ………..(Angles of a triangle)
⇒ ∠BAC + ∠BAC + 54° = 180° ………….(∵ AB = BC)
⇒ 2 ∠BAC = 180° − 54°
⇒ 2 ∠BAC = 126°
∴ ∠BAC =126°/2=63°
and ∠BCA = 63°
∠BAC + b = 180° …………..(Linear pair)
⇒ 63° + b = 180°
⇒ b = 180° − 63° = 117°
and ∠BCA + a = 180° …………(Linear pair)
∴ 63° + a = 180°
⇒ a = 180° − 63° = 117°
Hence,
a = 117°,
b = 117
Triangles ICSE Class-7th Concise Selina Mathematics Solutions Exercise – 15 C
Question 1.
Construct a ∆ABC such that:
(i) AB = 6 cm, BC = 4 cm and CA = 5.5 cm
(ii) CB = 6.5 cm, CA = 4.2 cm and BA = 51 cm
(iii) BC = 4 cm, AC = 5 cm and AB = 3.5 cm
Answer
(i)
Steps :
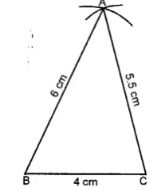
(i) Draw a line segment BC = 4 cm.
(ii) With centre B and radius 6 cm draw an arc.
(iii) With centre C and radius 5.5 cm, draw another arc intersecting the First are at A.
(iv) Join AB and AC.
∆ABC is the required triangle.
(ii)
Steps :
(i) Draw a line segment CB = 6.5 cm
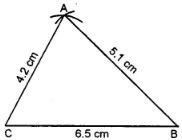
(ii) With centre C and radius 4.2 cm draw an arc.
(iii) With centre B and radius 5.1 cm draw another arc intersecting the first arc at A.
(iv) Join AC and AB.
∆ ABC is the required triangle.
(iii)
Steps :
(i) Draw a line segment BC = 4 cm.
(ii) With centre B and radius 3.5 cm, draw an arc.
(iii) With centre C and radius 5 cm, draw another arc which intersects the first arc at A.
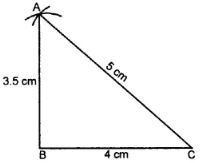
(iv) Join AB and AC.
∆ ABC is the required triangle.
Question 2.
Construct a A ABC such that:
(i) AB = 7 cm, BC = 5 cm and ∠ABC = 60°
(ii) BC = 6 cm, AC = 5.7 cm and ∠ACB = 75°
(iii) AB = 6.5 cm, AC = 5.8 cm and ∠A = 45°
Answer
(i)
Steps :
(i) Draw a line segment AB = 7 cm.

(ii) At B, draw a ray making an angle of 60° and cut off BC = 5 cm
(iii) Join AC.
∆ ABC is the required triangle.
(ii)
Steps :
(i) Draw a line segment BC = 6 cm.
(ii) At C, draw a ray making an angle of 75° and cut off CA = 5.7 cm.
(iii) join AB.
∆ ABC is the required triangle.

(iii)
Steps :
(i) Draw a line segment AB = 6.5 cm
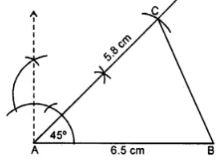
(ii) At A, draw a ray making an angle of 45° and cut off AC = 5.8 cm
(iii) Join CB.
∆ ABC is the required triangle.
Question 3.
Construct a ∆ PQR such that :
(i) PQ = 6 cm, ∠Q = 60° and ∠P = 45°. Measure ∠R.
(ii) QR = 4.4 cm, ∠R = 30° and ∠Q = 75°. Measure PQ and PR.
(iii) PR = 5.8 cm, ∠P = 60° and ∠R = 45°.
Measure ∠Q and verify it by calculations
Answer
(i)
Steps:
(i) Draw a line segment PQ = 6 cm.
(ii) At P, draw a ray making an angle of 45°
(iii) At Q, draw another ray making an angle of 60° which intersects the first ray at R.
∆ PQR is the required triangle. On measuring ∠R, it is 75°.
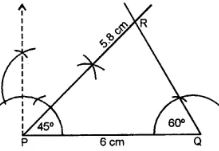
(ii)
Steps :
(i) Draw a line segment QR = 4.4 cm.
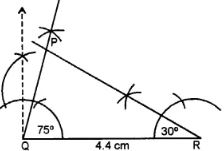
(ii) At Q, draw a ray making an angle of 75°
(iii) At R, draw another arc making an angle of 30°; which intersects the first ray at R
∆ PQR is the required triangle.
On measuring the lengths of PQ and PR, PQ = 2.1 cm and PR = 4. 4 cm.
(iii)
Steps of Construction :
(i) Draw a line segment PR = 5.8 cm
(ii) At P, construct an angle of 60°
(iii) At R, draw another angle of 45° meeting each other at Q.
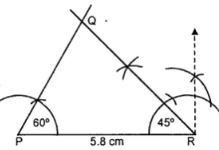
∆ PQR is the required triangle. On measuring ∠Q, it is 75°
Verification: We know that sum of angles of a triangle is 180°
∴∠P + ∠Q + ∠R = 180°
⇒ 60° + ∠Q + 45° = 180°
⇒ ∠Q + 105° = 180°
⇒ ∠Q = 180° – 105° = 75°.
Question 4.
Construct an isosceles A ABC such that:
(i) base BC = 4 cm and base angle = 30°
(ii) base AB = 6-2 cm and base angle = 45°
(iii) base AC = 5 cm and base angle = 75°.
Measure the other two sides of the triangle.
Answer
(i)
Steps:
We know that in an isosceles triangle base angles are equal.
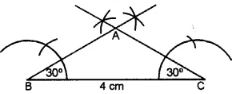
(i) Draw a line segment BC = 4 cm.
(ii) At B and C, draw rays making an angle of 30° each intersecting each other at A.
∆ ABC is the required triangle.
On measuring the equal sides each is 2.5 cm (approx.) in length.
(ii)
Steps:
We know that,
in an isosceles triangle, base angles are equal.
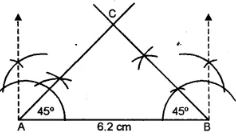
(i) Draw a line segment AB = 6.2 cm
(ii) At A and B, draw rays making an angle of 45° each which intersects each other at C.
∆ABC is the required triangle.
On measuring the equal sides, each is 4.3 cm (approx.) in length.
(iii)
Steps:
We know that,
the base angles of an isosceles triangle are equal.

(i) Draw a line segment AC = 5cm.
(ii) At A and C, draw rays making an angle of 75° each which intersects each other at B.
∆ ABC is the required triangle.
On measuring the equal sides, each is 9.3 cm in length.
Question 5.
Construct an isosceles ∆ABC such that:
(i) AB = AC = 6.5 cm and ∠A = 60°
(ii) One of the equal sides = 6 cm and vertex angle = 45°. Measure the base angles.
(iii) BC = AB = 5-8 cm and ZB = 30°. Measure ∠A and ∠C.
Answer
(i)
Steps:

(i) Draw a line segment AB = 6.5 cm.
(ii) At A, draw a ray making an angle of 60°.
(iii) Cut off AC = 6.5 cm
(iv) Join BC.
∆ ABC is the required triangle.
(ii)
Steps :
(i) Draw a line segment AB = 6 cm
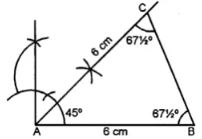
(ii) At A, construct an angle equal to 45°
(iii) Cut off AC = 6 cm
(iv) Join BC.
∆ ABC is the required triangle.
On measuring, ∠B and ∠C, each is equal 1° to, 67 1/2.
(iii)
Steps:
(i) Draw a line segment BC = 5.8 cm
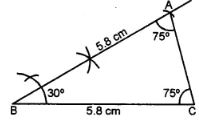
(ii) At B, draw a ray making an angle of 30°.
(iii) Cut off BA = 5.8 cm
(iv) Join AC.
∆ ABC is the required triangle On measuring ∠C and ∠A, each is equal to 75°.
Question 6.
Construct an equilateral A ABC such that:
(i) AB = 5 cm. Draw the perpendicular bisectors of BC and AC. Let P be the point of intersection of these two bisectors. Measure PA, PB and PC.
(ii) Each side is 6 cm.
Answer
(i)
Steps :
(i) Draw a line segment AB = 5 cm.
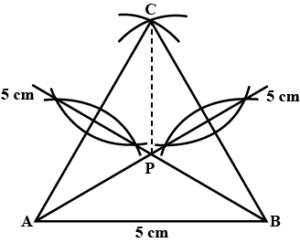
(ii) With centres A and B and radius 5 cm each, draw two arcs intersecting each other at C.
(iii) Join AC and BC ∆ ABC is the required triangle.
(iv) Draw the perpendicular bisectors of sides AC and BC which intersect each other at P.
(v) Join PA, PB, and PC.
On measuring, each is 2.8 cm.
(ii)
Steps :
(i) Draw a line segment AB = 6 cm.

(ii) At A and B as centre and 6 cm as radius draw two arcs intersecting each other at C.
(iii) Join AC and BC.
∆ ABC is the required triangle.
Question 7.
(i) Construct a ∆ ABC such that AB = 6 cm, BC = 4.5 cm and AC = 5.5 cm. Construct a circumcircle of this triangle.
(ii) Construct an isosceles ∆PQR such that PQ = PR = 6.5 cm and ∠PQR = 75°. Using ruler and compasses only construct a circumcircle to this triangle.
(iii) Construct an equilateral triangle ABC such that its one side = 5.5 cm.
Construct a circumcircle to this triangle.
Answer
(i)
Steps :
(i) Draw a line segment BC = 4.5 cm
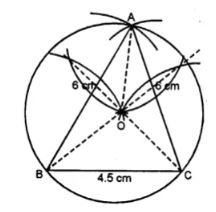
(ii) With centre B and radius 6 cm, draw are arc
(iii) With centre C and radius 5.5 cm, draw another arc intersecting the first arc at A.
(iv) Join AB and AC.
Δ ABC is the required triangle.
(v) Draw the perpendicular bisectors of AB and AC. Which intersects each other at O.
(vi) Join OB, OC and OA.
(vii) With centre O and radius OA, draw a circle which passes through A, B and C.
This is the required circumcircle of Δ ABC.
(ii)
Steps :
(i) Draw a line segment PQ = 6.5 cm
(ii) At Q, draw a ray making an angle of 75°.

(iii) Through P, with a radius of 6.5 cm, draw an arc which intersects the angle ray at R.
(iv) Join PR,
Δ PQR is the required triangle.
(v) Draw the perpendicular bisectors of sides PQ and PR intersecting each other at O.
(vi) Join OP, OQ and OR.
(vii) With centre O and radius equal to OP or OQ or OR draw a circle which passes through P, Q and R. This is the required circumcircle of Δ PQR
(iii)
Steps :
(i) Draw a line segment AB = 5.5 cm
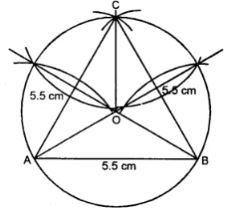
(ii) With centres A and B and radius 5.5 cm, draw two arcs intersecting each other at C.
(iii) Join AC and BC.
Δ ABC is the required triangle.
(iv) Draw perpendicular bisectors of sides AC and BC which intersect each other at O.
(v) Join OA, OB and OC.
(vi) With centre O and radius OA or OB or OC, draw a circle which passes through A, B and C. This is the required circumcircle.
Question 8.
(i) Construct a ∆ABC such that AB = 6 cm, BC = 5.6 cm and CA = 6.5 cm. Inscribe a circle to this triangle and measure its radius.
(ii) Construct an isosceles ∆ MNP such that base MN = 5.8 cm, base angle MNP = 30°. Construct an incircle to this triangle and measure its radius.
(iii) Construct an equilateral ∆DEF whose one side is 5.5 cm. Construct an incircle to this triangle.
(iv) Construct a ∆ PQR such that PQ = 6 cm, ∠QPR = 45° and angle PQR = 60°. Locate its incentre and then draw its incircle.
Answer
(i)
Steps :
(i) Draw a line segment AB = 6 cm.
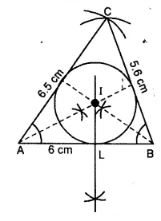
(ii) With centre A and radius 6.5 cm and with centre B and radius 5.6 cm, draw arcs intersecting each other at C.
(iii) Join AC and BC.
(iv) Draw the angle bisector of ∠A and ∠B intersecting each other at I.
(v) From I, draw IL ⊥ AB
(vi) With centre I and radius IL, draw a circle which touches the sides of Δ ABC internally.
On measuring the required incircle whose radius is 1.6 cm.
(ii)
Steps :
(i) Draw a line segment MN = 5.8 cm.
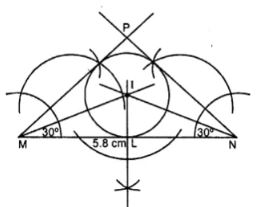
(ii) At M and N, draw two rays making an angle of 30° each which intersect each other at P.
(iii) Now draw the angle bisectors of ∠M and ∠N which intersects each other at I.
(iv) From I, draw the perpendicular IL on MN.
(v) With centre I and radius IL, draw a circle which touches the sides of the Δ PMN internally.
On measuring the required incircle and its radius is 0.6 cm.
(iii)
Steps :
(i) Draw a line segment BC = 5.5 cm.

(ii) With centres B and C and radius 5.5 cm each draw two arcs intersecting each other at A.
(iii) Join AB and AC.
(iv) Draw the perpendicular bisectors of ∠B and ∠C intersecting each other at I.
(v) From I, draw IL ⊥ BC
(vi) With centre I and radius IL, draw a circle which touches the sides of the Δ ABC internally.
This is the required incircle.
(iv)
Steps :
(i) Draw a line segment PQ = 6 cm.
(ii) At P draw rays making an angle of 45° and at Q, making an angle of 60°, intersecting each other at R.
(iii) Draw the bisectors of ∠P and ∠Q intersecting each other at I.
(iv) From I, draw IL ⊥ PQ.

(v) With centre I and radius IL, draw a circle which touches the sides of Δ PQR internally. This is the required incircle whose I is incentre.
— End of Triangles ICSE Class-7th Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -7
Thanks


