AP MCQ Type Questions ICSE Class-10 Maths for Sem-1. These MCQ / Objective Type Questions of Arithmetic Progression is based on latest reduced syllabus according 2021-22 session on bifurcated pattern. Main motto of MCQ Type Question is cracking the next upcoming exam of council. Visit official website CISCE for detail information about ICSE Board Class-10 Maths
ICSE Class-10 Maths Arithmetic Progression (AP) MCQ Type Questions
| Board | ICSE |
| Class | 10th ( x ) |
| Subject | Maths |
| Chapter | Arithmetic Progression (AP) |
| Syllabus | on bifurcated syllabus (after reduction) |
| bifurcated pattern |
Semester-1 |
| Session | 2021-22 |
| Topic | MCQ / Objective Type Question |
Arithmetic Progression MCQ Type Questions ICSE Class-10 Maths for Sem-1
Question 1 The sum of first n terms of the series a, 3a, 5a, …….. is
(a) na
(b) (2n – 1) a
(c) n²a
(d) n²a²
Answer: (c) n²a
Question 2 Which term of the AP: 27, 24, 21, ……… is zero?
(a) 8th
(b) 10th
(c) 9th
(d) 11th
Answer:: (b) 10th
Question 3 The 6th term from the end of the AP: 5, 2, -1, -4, …., -31, is
(a) -25
(b) -22
(c) -19
(d) -16
Answer:: (d) -16
Question 4. Find the 15th term of an AP -2, -5, -8, ….
(a) 70
(b) -44
(c) 72
(d) 64
Answer:: (b) -44
Question 5 The sum of first ten natural number is
(a) 55
(b)155
(c) 65
(d) 110
Answer:: (a) 55
Question 6 If the sum of the first m terms of an AP is n and the sum of its n terms is m, then the sum of its (m + n) terms will be
(a) m + n
(b) -(m + n)
(c) m – n
(d) 0
Answer: (b) -(m + n)
Question-7 The sum of the first 2n terms of the AP: 2, 5, 8, …. is equal to sum of the first n terms of the AP: 57, 59, 61, … then n is equal to.
(a) 10
(b) 11
(c) 12
(d) 13
Answer:: (b) 11
Question -8 : If p – 1, p + 3, 3p – 1 are in AP, then p is equal to
(a) 4
(b) -4
(c) 2
(d) -2
Answer: (a) 4
Question 9 The 10th term of the sequence √3, 12‾‾‾√, 27‾‾‾√; …… is
(a) 243‾‾‾‾√
(b) 300‾‾‾‾√
(c) 363‾‾‾‾√
(d) 432
Answer: (b) 300‾‾‾‾√
Question 10 If the sum of first n terms of an AP is An + Bn² where A and B are constants. The common difference of AP will be
(a) A + B
(b) A – B
(c) 2A
(d) 2B
Answer: (d) 2B
Question 11 . If nth term of an AP is 7 – 4n, then its common difference is
(a) 4
(b) -4
(c) 3
(d) 11
Answer:: (d) 11
Question 12: the 20th term of the AP -5, -3, -1, 1, is
(a) 33
(b) 30
(c) 20
(d) 25
Answer:: (a) 33
Question 13. First four terms of the sequence an = 2n + 3 are
(a) 3, 5, 7, 9
(b) 5, 7, 9, 11
(c) 5, 8, 11, 14
(d) 1, 3, 5, 7
Answer:: (b) 5, 7, 9, 11
Question 14 Next term of the AP √2, 3√2, 5√2, ……. is
(a) 2√7
(6) 6√2
(c) 9√2
(d) 7√2
Answer:: (d) 7√2
Question15 The sum of the first 15 multiples of 8 is
(a) 920
(b) 860
(c) 900
(d) 960
Answer: : (d) 960
Question 16. In an AP if a = 1, an = 20 and Sn = 399, then n is
(a) 19
(b) 21
(c) 38
(d) 42
Answer: (c) 38
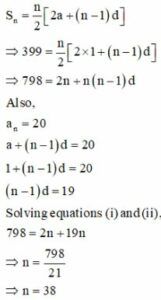
Question-15. If the numbers n – 2, 4n – 1 and 5n +2 are in AP, then the value of n is:
(a) 1
(b) 2
(c) − 1
(d) − 2
Answer: (a) 1
Hint
Let a = n – 2
b = 4n – 1
c = 5n + 2
Since the terms are in A.P,
Therefore,
2b = a + c
⇒ 2 (4n – 1) = n – 2 + 5n + 2
⇒ 8n – 2 = 6n
⇒ 2n = 2
⇒ n = 1
Question 16: 37th term of the AP: √x, 3√x, 5√x, …….. is
(a) 37 √x
(b) 39 √x
(c) 73 √x
(d) 75 √x
Answer: (c) 73 √x
Question 17. Which term of the AP: 92, 88, 84, 80 … is 0?
(a) 23
(b) 32
(c) 22
(d) 24
Answer: (d) 24
Question-18 . If 7 times the 7th term of an AP is equal to 11 times its 11th term, then its 18th term will be
(a) 7
(b) 11
(c) 18
(d) 0
Answer:(d) 0
Hint
According to question
7(a + 6d) = 11(a + 10d)
⇒ 7a + 42d = 11a + 110d
⇒ 4a + 68d = 0
⇒ 4(a + 17d) = 0
⇒ a + 17d = 0
Therefore,
a18 = a + 17d
a18 = 0
Question-19 Two APs have the same common difference. The first term of one of these is –1 and that of the other is – 8. Then the difference between their 4th terms is
(a) –1
(b) – 8
(c) 7
(d) –9
Answer: (c) 7
Hint
The 4th term of first series is
a4 = a1 + 3d
The 4th term of another series is
a`4 = a2 + 3d
Now,
As, a1 = –1, a2 = –8
Therefore,
a4 – a`4 = (–1 + 3d) – (–8 + 3d)
a4 – a`4 = 7
Question 20. If the common difference of an AP is 5, then what is a18 – a13?
(a) 5
(b) 20
(c) 25
(d) 30
Answer: (c) 25
Hint
Since, d = 5
a18 – a13 = a + 17d – a – 12d
= 5d = 5 × 5 = 25
Question-21 . The sum of first 16 terms of the AP: 10, 6, 2,… is
(a) –320
(b) 320
(c) –352
(d) –400
Answer: (a) –320
Question-22 The sum of first five multiples of 3 is
(a) 45
(b) 55
(c) 65
(d) 75
Answer: (a) 45
Question-23 The middle most term (s) of the AP:–11, –7, –3, …, 49 is:
(a) 18, 20
(b) 19, 23
(c) 17, 21
(d) 23, 25
Answer: (c) 17, 21
Hint
Here, a = −11
d = − 7 – (−11) = 4
And an = 49
an = a + (n – 1)d
⇒ 49 = −11 + (n – 1)4
⇒ 60 = (n – 1)4
⇒ n = 16
As n is an even number, there will be two middle terms which are16/2th and [(16/2)+1]th, i.e. the 8th term and the 9th term.
a8 = a + 7d = – 11 + 7 × 4 = 17
a9 = a + 8d = – 11 + 8 × 4 = 21
Question-24 If the 2nd term of an AP is 13 and the 5th term is 25, what is its 7th term?
(a) 30
(b) 33
(c) 37
(d) 38
Answer: (b) 33
Hint
a2 = 13
a5 = 25
⇒ a + d = 13 ….(i)
⇒ a + 4d = 25 ….(ii)
Solving equations (i) and (ii),
a = 9; d = 4
Therefore,
a7 = 9 + 6 × 4
a7 = 9 + 24
a7 = 33
Question-25. The 21st term of the AP whose first two terms are –3 and 4 is
(a) 17
(b) 137
(c) 143
(d) –143
Answer: (b) 137
Hint
First two terms are –3 and 4
a = −3
a + d = 4
⇒ d = 4 − a
⇒ d = 4 + 3
⇒ d = 7
a21 = a + (21 – 1)d
a21 = –3 + (20)7
a21 = 137
Question-26 The first four terms of an AP, whose first term is –2 and the common difference is –2, are
(a) – 2, 0, 2, 4
(b) – 2, 4, – 8, 16
(c) – 2, – 4, – 6, – 8
(d) – 2, – 4, – 8, –16
Answer: (c) – 2, – 4, – 6, – 8
Hint
Let the first four terms of an A.P are a, a+d, a+2d and a+3d
Given that the first termis −2 and difference is also −2, then the A.P would be:
– 2, (–2–2), [–2 + 2 (–2)], [–2 + 3(–2)]
= –2, –4, –6, –8
Question-27 The nth term of an A.P. is given by an = 3 + 4n. The common difference is
(a) 7
(b) 3
(c) 4
(d) 1
Answer: (c) 4
Hint: : We have an = 3 + 4n
∴ an+1 = 3 + 4(n + 1) = 7 + 4n
∴ d = an+1 – an
= (7 + 4n) – (3 + 4n)
= 7 – 3
= 4
Question-28 If p, q, r and s are in A.P. then r – q is
(a) s – p
(b) s – q
(c) s – r
(d) none of these
Answer:(c) s – r
Hint : Since p, q, r, s are in A.P.
∴ (q – p) = (r – q) = (s – r) = d (common difference)
Question-29 If the sum of three numbers in an A.P. is 9 and their product is 24, then numbers are
(a) 2, 4, 6
(b) 1, 5, 3
(c) 2, 8, 4
(d) 2, 3, 4
Answer: (d) 2, 3, 4
Hint : Let three numbers be a – d, a, a + d
∴ a – d +a + a + d = 9
⇒ 3a = 9
⇒ a = 3
Also (a – d) . a . (a + d) = 24
⇒ (3 -d) .3(3 + d) = 24
⇒ 9 – d² = 8
⇒ d² = 9 – 8 = 1
∴ d = ± 1
Hence numbers are 2, 3, 4 or 4, 3, 2
Question -30 The (n – 1)th term of an A.P. is given by 7,12,17, 22,… is
(a) 5n + 2
(b) 5n + 3
(c) 5n – 5
(d) 5n – 3
Answer: (d) 5n – 3
Hint Here a = 7, d = 12-7 = 5
∴ an-1 = a + [(n – 1) – l]d = 7 + [(n – 1) -1] (5) = 7 + (n – 2)5 = 7 + 5n – 10 = 5M – 3
Question -31 The nth term of an A.P. 5, 2, -1, -4, -7 … is
(a) 2n + 5
(b) 2n – 5
(c) 8 – 3n
(d) 3n – 8
Answer: (c) 8 – 3n
Hint Here a = 5, d = 2 – 5 = -3
an = a + (n – 1)d = 5 + (n – 1) (-3) = 5 – 3n + 3 = 8 – 3n
Question-32 The 10th term from the end of the A.P. -5, -10, -15,…, -1000 is
(a) -955
(b) -945
(c) -950
(d) -965
Answer: (a) -955
Hint Here l = -1000, d = -10 – (-5) = -10 + 5 = – 5
∴ 10th term from the end = l – (n – 1 )d = -1000 – (10 – 1) (-5) = -1000 + 45 = -955
Question-33 Find the sum of 12 terms of an A.P. whose nth term is given by an = 3n + 4
(a) 262
(b) 272
(c) 282
(d) 292
Answer: (a) 262
Hint Here an = 3n + 4
∴ a1 = 7, a2 – 10, a3 = 13
∴ a= 7, d = 10 – 7 = 3
∴ S12 = 12/2 [2 × 7 + (12 – 1) ×3] = 6[14 + 33] = 6 × 47 = 282
Question-34 The sum of all two digit odd numbers is
(a) 2575
(b) 2475
(c) 2524
(d) 2425
Answer: (b) 2475
Hint All two digit odd numbers are 11,13,15,… 99, which are in A.P.
Since there are 90 two digit numbers of which 45 numbers are odd and 45 numbers are even
∴ Sum = (45/2)[11 + 99] = (45/ 2) × 110 = 45 × 55 = 2475
Question-35 . The sum of first n odd natural numbers is
(a) 2n²
(b) 2n + 1
(c) 2n – 1
(d) n
Answer: (d) n
Hint Required Sum = 1 + 3 + 5 + … + upto n terms.
Here a = 1, d = 3 – 1 = 2
Sum = 𝑛/2 [2 × 1 + (n – 1) × 2] = 𝑛2[2 + 2n – 2] = 𝑛2 × 2n = n²Reason: All two digit odd numbers are 11,13,15,… 99, which are in A.P.
Since there are 90 two digit numbers of which 45 numbers are odd and 45 numbers are even
∴ Sum = 45/2 [11 + 99]
= (45/ 2) × 110
= 45 × 55 = 2475
Question-36 If (p + q)th term of an A.P. is m and (p – q)tn term is n, then pth term is

Answer: (d) 1/2 (m+n)
Hint : Let a is first term and d is common difference
∴ ap + q = m
ap – q = n
⇒ a + (p + q – 1)d = m = …(i)
⇒ a + (p – q – 1)d = m = …(ii)
On adding (i) and (if), we get
2a + (2p – 2)d = m + n
⇒ a + (p -1)d = 𝑚+𝑛 /2 …[Dividing by 2
∴ an = 𝑚+𝑛 /2
Question-37 . If a, b, c are in A.P. then 𝑎−𝑏𝑏−𝑐 is equal to
(a) 1
(b) b/2
(c) a/c
(d) c/a
Answer: (a) 1
Hint Since a, b, c are in A.P.
∴ b – a = c – b
⇒ 𝑏−𝑎 / 𝑐−𝑏 = 1
⇒ 𝑎−𝑏 / 𝑏−𝑐 = 1
Question-38. The number of multiples lie between n and n² which are divisible by n is
(a) n + 1
(b) n
(c) n – 1
(d) n – 2
Answer: (d) n – 2
Hint :- Multiples of n from 1 to n² are n × 1, n × 2, n × 3, …, m× n
∴ There are n numbers
Thus, the number of mutiples of n which lie between n and n² is (n – 2) leaving first and last in the given list: Total numbers are (n – 2)
Question-39 If a, b, c, d, e are in A.P., then the value of a – 4b + 6c – 4d + e is
(a) 0
(b) 1
(c) -1.
(d) 2
Answer:( a) 0
Hint : Let common difference of A.P. be x
∴ b = a + x, c = a + 2x, d = a + 3x and e = a + 4x
Given equation n-4b + 6c-4d + c
= a – 4(a + x) + 6(A + 2r) – 4(n + 3x) + (o + 4.v)
= a – 4a – 4x + 6a + 12x – 4a – 12x + a + 4x = 8a – 8a + 16x – 16x = 0
Question-40 nth term of the sequence a, a + d, a + 2d,… is
(a) a + nd
(b) a – (n – 1)d
(c) a + (n – 1)d
(d) n + nd
Answer:(a) a + nd
Hint : an = a + (n – 1)d
Question-41 The 10th term from the end of the A.P. 4, 9,14, …, 254 is
(a) 209
(b) 205
(c) 214
(d) 213
Answer: (a) 209
Hint Here l – 254, d = 9-4 = 5
∴ 10th term from the end = l – (10 – 1 )d = 254 -9d = 254 = 9(5) = 254 – 45 = 209
Question-42 . If 2x, x + 10, 3x + 2 are in A.P., then x is equal to
(a) 0
(b) 2
(c) 4
(d) 6
Answer: (d) 6
Hint: Since 2x, x + 10 and 3x + 2 are in A.P.
∴ 2(x + 10) = 2x + (3x + 2)
⇒ 2x + 20 – 5x + 2
⇒ 2x – 5x = 2 – 20
⇒ 3x = 18
⇒ x = 6
Question-43 The sum of all odd integers between 2 and 100 divisible by 3 is
(a) 17
(b) 867
(c) 876
(d) 786
Answer: (b) 867
Hint The numbers are 3, 9,15, 21, …, 99
Here a = 3, d = 6 and an = 99
∴ an = a + (n – 1 )d
⇒ 99 = 3 + (n – 1) x 6
⇒ 99 = 3 + 6n – 6
⇒ 6n = 102
⇒ n = 17
Required Sum = 𝑛/2 [a + an]
= 17/2 [3 + 99]
= 17/2 × 102
= 867
Question-44 . If the numbers a, b, c, d, e form an A.P., then the value of a – 4b + 6c – 4d + e is
(a) 0
(b) 1
(c) -1
(d) 2
Answer:(a) 0
Hint Let x be the common difference of the given AP
∴ b = a + x, c = a + 2x, d = a + 3x and e = a + 4x
∴ a – 4b + 6c – 4d + e = a – 4 (a + x) + 6(a + 2x) – 4(a + 3x) + (a + 4x)
= a – 4a – 4x + 6a + 12x – 4a – 12x + a + 4x = 8a – 8a + 16x – 16x = 0
Question-45 If 7 times the 7th term of an A.P. is equal to 11 times its 11th term, then 18th term is
(a) 18
(b) 9
(c) 77
(d) 0
Answer: (d) 0
Hint We have 7a7 = 11a11
⇒ 7[a + (7 – 1)d] = 11[a + (11 – 1 )d]
⇒ 7(a + 6d) = 11(a + 10d)
⇒ 7a + 42d = 11a + 110d
⇒ 4a = -68d
⇒ a = -17d
∴ a18 = a + (18 – 1)d = a + 17d = -17d + 17d = 0
Question-46 In an Arithmetic Progression, if a = 28, d = -4, n = 7, then an is:
(a) 4
(b) 5
(c) 3
(d) 7
Answer: (a) 4
Hint For an AP,
an = a+(n-1)d
= 28+(7-1)(-4)
= 28+6(-4)
= 28-24
an=4
Question-47 If a = 10 and d = 10, then first four terms will be:
(a) 10, 30, 50, 60
(b) 10, 20, 30, 40
(c) 10, 15, 20, 25
(d) 10, 18, 20, 30
Answer: (b) 10, 20, 30, 40
Hint : a = 10, d = 10
a1 = a = 10
a2 = a1+d = 10+10 = 20
a3 = a2+d = 20+10 = 30
a4 = a3+d = 30+10 = 40
Question-48 The first term and common difference for the A.P. 3, 1, -1, -3 is:
(a) 1 and 3
(b) -1 and 3
(c) 3 and -2
(d) 2 and 3
Answer: (c) 3 and -2
Hint: First term, a = 3
Common difference, d = Second term – First term
⇒ 1 – 3 = -2
⇒ d = -2
Question-49 30th term of the A.P: 10, 7, 4, …, is
(a) 97
(b) 77
(c) -77
(d) -87
Answer: (c) -77
Hint Given,
A.P. = 10, 7, 4, …
First term, a = 10
Common difference, d = a2 − a1 = 7−10 = −3
As we know, for an A.P.,
an = a +(n−1)d
Putting the values;
a30 = 10+(30−1)(−3)
a30 = 10+(29)(−3)
a30 = 10−87 = −77
Question-50 The11th term of the A.P. -3, -1/2, 2 …. Is
(a) 28
(b) 22
(c) -38
(d) -48
Answer: (b) 22
Hint: A.P. = -3, -1/2, 2 …
First term a = – 3
Common difference, d = a2 − a1 = (-1/2) -(-3)
⇒(-1/2) + 3 = 5/2
Nth term;
an = a+(n−1)d
a11 = 3+(11-1)(5/2)
a11 = 3+(10)(5/2)
a11 = -3+25
a11 = 22
Question-51 The missing terms in AP: __, 13, __, 3 are:
(a) 11 and 9
(b) 17 and 9
(c) 18 and 8
(d) 18 and 9
Answer: (c)
Hint a2 = 13 and
a4 = 3
The nth term of an AP;
an = a+(n−1) d
a2 = a +(2-1)d
13 = a+d ………………. (i)
a4 = a+(4-1)d
3 = a+3d ………….. (ii)
Subtracting equation (i) from (ii), we get,
– 10 = 2d
d = – 5
Now put value of d in equation 1
13 = a+(-5)
a = 18 (first term)
a3 = 18+(3-1)(-5)
= 18+2(-5) = 18-10 = 8 (third term).
Question-52 Which term of the A.P. 3, 8, 13, 18, … is 78?
(a) 12th
(b) 13th
(c) 15th
(d) 16th
Answer: (d) (d) 16th
Hint Given, 3, 8, 13, 18, … is the AP.
First term, a = 3
Common difference, d = a2 − a1 = 8 − 3 = 5
Let the nth term of given A.P. be 78. Now as we know,
an = a+(n−1)d
Therefore,
78 = 3+(n −1)5
75 = (n−1)5
(n−1) = 15
n = 16
Question-53 The 21st term of AP whose first two terms are -3 and 4 is:
(a) 17
(b) 137
(c) 143
(d) -143
Answer: (b) 137
Hint: First term = -3 and second term = 4
a = -3
d = 4-a = 4-(-3) = 7
a21=a+(21-1)d
=-3+(20)7
=-3+140
=137
Question-54. If 17th term of an A.P. exceeds its 10th term by 7. The common difference is:
(a) 1
(b) 2
(c) 3
(d) 4
Answer: (a) 1
hint : Nth term in AP is:
an = a+(n-1)d
a17 = a+(17−1)d
a17 = a +16d
In the same way,
a10 = a+9d
Given,
a17 − a10 = 7
Therefore,
(a +16d)−(a+9d) = 7
7d = 7
d = 1
Therefore, the common difference is 1.
Question-55 The number of multiples of 4 between 10 and 250 is:
(a) 50
(b) 40
(c) 60
(d) 30
Answer: (c) 60
hint The multiples of 4 after 10 are:
12, 16, 20, 24, …
So here, a = 12 and d = 4
Now, 250/4 gives remainder 2. Hence, 250 – 2 = 248 is divisible by 2.
12, 16, 20, 24, …, 248
So, nth term, an = 248
As we know,
an = a+(n−1)d
248 = 12+(n-1)×4
236/4 = n-1
59 = n-1
n = 60
Question-56 20th term from the last term of the A.P. 3, 8, 13, …, 253 is:
(a) 147
(b) 151
(c) 154
(d) 158
Answer: (d) 158
hint: Given, A.P. is 3, 8, 13, …, 253
Common difference, d= 5.
In reverse order,
253, 248, 243, …, 13, 8, 5
So,
a = 253
d = 248 − 253 = −5
n = 20
By nth term formula,
a20 = a+(20−1)d
a20 = 253+(19)(−5)
a20 = 253−95
a20 = 158
Question-57. The sum of the first five multiples of 3 is:
(a) 45
(b) 55
(c) 65
(d) 75
Answer: (a) 45
hint The first five multiples of 3 is 3, 6, 9, 12 and 15
a=3 and d=3
n=5
Sum, Sn = n/2[2a+(n-1)d]
S5 = 5/2[2(3)+(5-1)3]
=5/2[6+12]
=5/2[18]
=5 x 9
= 45
Question-58 The 10th term of the AP: 5, 8, 11, 14, … is
(a) 32
(b) 35
(c) 38
(d) 185
Answer: (a) 32
hint
Given AP: 5, 8, 11, 14,….
First term = a = 5
Common difference = d = 8 – 5 = 3
nth term of an AP = an = a + (n – 1)d
Now, 10th term = a10 = a + (10 – 1)d
= 5 + 9(3)
= 5 + 27
= 32
Question-59. In an AP, if d = -4, n = 7, an = 4, then a is
(a) 6
(b) 7
(c) 20
(d) 28
Answer: (d) 28
hint d = -4, n = 7, an = 4
We know that,
an = a + (n – 1)d
4 = a + (7 – 1)(-4)
4 = a + 6(-4)
4 = a – 24
⇒ a = 4 + 24 = 28
Question-60 The list of numbers –10, –6, –2, 2,… is
(a) an AP with d = –16
(b) an AP with d = 4
(c) an AP with d = –4
(d) not an AP
Answer: (b) an AP with d = 4
hint –10, –6, –2, 2,…
Let a1 = -10, a2 = -6, a3 = -3, a4 = 2
a2 – a1 = -6 – (-10) = 4
a3 – a2 = -2 – (-6) = 4
a4 – a3 = 2 – (-2) = 4
The given list of numbers is an AP with d = 4.
Question-61 If the 2nd term of an AP is 13 and the 5th term is 25, then its 7th term is
(a) 30
(b) 33
(c) 37
(d) 38
Answer: (b) 33
hint a2 = 13
a + d = 13
a = 13 – d….(i)
a5 = 25
a + 4d = 25….(ii)
Substituting (i) in (ii),
13 – d + 4d = 25
3d = 12
d = 4
So, a = 13 – 4 = 9
a7 = a + 6d = 9 + 6(4) = 9 + 24 = 33
Question-62 Which term of the AP: 21, 42, 63, 84,… is 210?
(a) 9th
(b) 10th
(c) 11th
(d) 12th
Answer: (b) 10th
hint :
21, 42, 63, 84,…
a = 21
d = 42 – 21 = 21
an = 210
a + (n – 1)d = 210
21 + (n – 1)(21) = 210
21 + 21n – 21 = 210
21n = 210
n = 10
Question-63 What is the common difference of an AP in which a18 – a14 = 32?
(a) 8
(b) -8
(c) -4
(d) 4
Answer: (a) 8
hint
a18 – a14 = 32
We know that, an = a + (n – 1)d
So,
a + 17d – (a + 13d) = 32
17d – 13d = 32
4d = 32
d = 8
Question-64 The sum of first 16 terms of the AP: 10, 6, 2,… is
(a) –320
(b) 320
(c) –352
(d) –400
Answer: (a) -320
hint Given AP: 10, 6, 2,…
Here, a = 10, d = -4
Sum of first n terms = Sn = (n/2)[2a + (n – 1)d]
The sum of first 16 terms = S16 = (16/2)[2(10) + (16 – 1)(-4)]
= 8[20 + 15(-4)]
= 8(20 – 60)
= 8(-40)
= -320
–: End of AP MCQ Type Questions ICSE Class-10 Maths :-
-: also visit :-
- ICSE MCQs for Class-10 Subject-Wise / Chapter-Wise
- ICSE Class-10 Text book Solutions, Notes , Syllabus, Paper, Notes
Please share with your ICSE friends if it is helpful
Thanks



things are not proper in that
pls check your answers site= https://icsehelp.com/ap-mcq-type-questions-class-10-icse-maths-sem-1/
ok
pls check your ques and ans
update if any
q3 is wrong pls make it correct
ok