Constructions ICSE Class-8th Concise Selina Solutions Mathematics Solutions Chapter-18 . We provide step by step Solutions of Exercise / lesson-18 Constructions (Using ruler and compass only) for ICSE Class-8 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-18 A, Exe-18 B Exe-18 C and Exe-18 D to develop skill and confidence . Visit official Website CISCE for detail information about ICSE Board Class-8.
Constructions ICSE Class-8th Concise Selina Solutions Mathematics Solutions Chapter-18 (Using ruler and compass only)
–: Select Topics :–
Exercise – 18 A Constructions (Using ruler and compass only) ICSE Class-8th Concise Selina Mathematics
Question 1.
Given below are the angles x and y.

Without measuring these angles, construct :
(i) ∠ABC = x + y
(ii) ∠ABC = 2x + y
(iii) ∠ABC = x + 2y
Answer
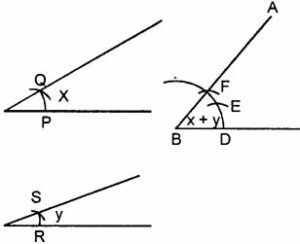
(i) Steps of Construction :
- With B as the centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the arc x at points P and Q and arms of angle y at points R and S.
- From the arc, with centre B, cut DE = PQ arc of x and EF = RS arc of y
- Join BF and produce up to point A.
Thus ∠ABC = x + y - Draw a line segment BC of any suitable length.
(ii) Steps of Construction :
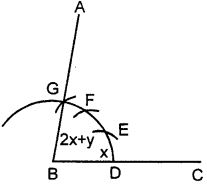
Proceed in exactly the same way as in part(i)
takes DE = PQ = arc of x.
EF = PQ = arc of x and FG = RS = arc of y.
Join BG and produce it up to A.
Thus ∠ABC = x + x+ y = 2x + y
(iii) Steps of Construction :
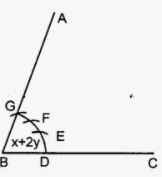
Proceed in exactly the same way as in (ii)
taking DE = PQ = arc of x. and EF = RS = arc of y and FG = RS = arc of y.
4. Join BF and produce up to point A.
Thus ∠ABC = x + y + y = x + 2y
Question 2.
Given below are the angles x, y and z.
Without measuring these angles construct :
(i) ∠ABC = x + y + z
(ii) ∠ABC = 2x + y + z
(iii) ∠ABC = x + 2y + z

Answer
(i) Steps of Construction :
1. Draw line segment BC of any suitable length.

- With B as a centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q and arms of the angle y at points R and S and arms of the angle z at the points L and M.
- From the arc, with centre B, cut
DE = PQ = arc of x, EF = RS = arc of y and FG = LM = arc of z. - Join BG and produce it up to A.
Then ∠ABC = x + y + z
(ii) Proceed as in part
(i) up to step 2.
3. From the arc, with centre B, cut

DE = 2PQ = 2 arc of x
EF = RS = arc of y
FG = LM = arc of z
4. Join BG and produce it up to point A
Then ∠ABC = 2x + y + z
(iii) proceed as in
(i) up to step 2
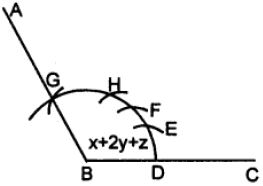
3. Here cut arc DE = arc PQ = arc of x arc EF = 2 arc RS = 2 arc of y arc FG = arc LM = arc of z.
4. Join BG and produce it up to A
5. Then ∠ABC = x + 2y + z
Question 3.
Draw a line segment BC = 4 cm. Construct angle ABC = 60°.
Answer

- Draw a line segment BC = 4 cm
- With B as a centre, draw an arc of any suitable radius which cuts BC at point D.
- With D as a centre, and the same radius as in step 2, draw one more arc which cuts the previous arc at point E.
- Join BE and produce it to point A.
Thus ∠ABC = 60°
Question 4.
Construct angle ABC = 45° in which BC = 5 cm and AB = 4.6 cm.
Answer
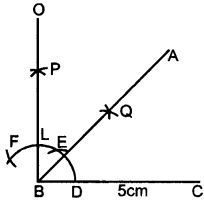
- Draw a line segment BC = 5 cm
- Taking B as centre, draw an arc of any suitable radius, which cuts BC at the point D.
- With D as the centre and the same radius, as taken in step 2, draw an arc which cuts the previous arc at point E.
- With E as the centre and the same radius, draw one more arc which cuts the first arc at point F.
- With E and F as centres and radii equal to more than half the distance between E at F, draw an arc which cut each other at point P.
- Join BP to meet EF at L and produce to point O. Then ∠OBC = 90°
- Draw BA, the bisector of angle OBC. [With D, L as centres and suitable radius draw two arc meeting each other at Q produced it to R]
=> ∠ABC = 45° [∴ BA is bisector of ∠OBC ∴ ∠ABC = = 45°] - From BR cut arc AB = 4.6 cm
Question 5.
Construct angle ABC = 90°. Draw BP, the bisector of angle ABC. State the measure of angle PBC.
Answer
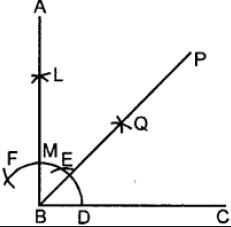
Draw ∠ABC = 90°
Draw bisector of ∠ABC
Then ∠PBC = (1/2) (90°) = 45°
Question 6.
6. Draw angle ABC of any suitable measure.
(i) Draw BP, the bisector of angle ABC.
(ii) Draw BR, the bisector of angle PBC and draw BQ, the bisector of angle ABP.
(iii) Are the angles ABQ, QBP, PBR and RBC equal?
(iv) Are the angles ABR and QBC equal ?
Answer
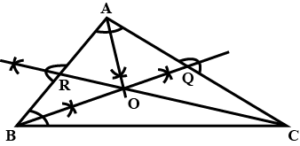
1. Draw any angle
2. Taking as center, construct an arc meeting at and at .
3. Taking as centers construct two arc of equal radii meeting each other a the point
4. Now join . is the bisector of
5. In the same way draw , the bisector of and draw as the bisector of [with the same method as in step ]
6. Then
7. and
Selina Solutions Exe-18 B Constructions (Using ruler and compass only) for ICSE Class-8th Concise Mathematics
Question 1.
Draw a line segment AB of length 5.3 cm. Using two different methods bisect AB.
Answer
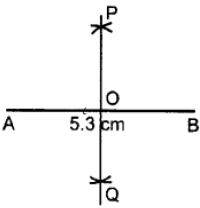
- Draw a line segment AB = 5.3 cm
- With A as centre and radius equal to more than half of AB, draw arcs on both sides of AB.
- With B as the centre and with the same radius as taken in step 2, draw arcs on both sides of AB.
- Let the arcs intersect each other at points P and Q.
- Join P and Q.
- The line PQ cuts the given line segment AB at point O.
Thus, PQ is a bisector of AB such that
OA = OB = 1/2AB
Question 2.
Draw a line segment PQ = 4.8 cm. Construct the perpendicular bisector of PQ.
Answer
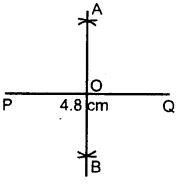
- Draw a line segment PQ = 4.8 cm.
- With P as centre and radius equal than half of PQ, draw an arc on both the PQ.
- With Q as the centre and the same radius as taken in step 2, draw arcs on both sides of PQ.
- Let the arcs intersect each other at point A and B
- Join A and B.
- The line AB cuts the line segment PQ at the point O. Here OP = OQ and ∠AOQ = 90°. Then the line AB is a perpendicular bisector of PQ.
Question 3.
In each of the following, draw perpendicular through point P to the line segment AB :

Answer
(i) Steps of the Construction :
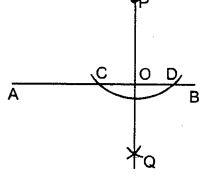
- With P as a centre, draw an arc of a suitable radius which cuts AB at points C and D.
- With C and D as centres, draw arcs of equal radii and let these arcs intersect each other at point Q.
[The radius of these arcs must be more than half of CD and both the arcs must be drawn on the other side] - Join P and Q
- Let PQ cut AB at the point O.
Thus, OP is the required perpendicular clearly, ∠AOP = ∠BOP = 90°
(ii) Steps of the Construction :
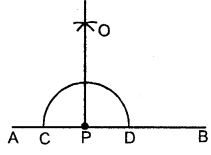
- With P as a centre, draw an arc of any suitable radius which cuts AB at points C and D.
- With C and D as centres, draw arcs of equal radii. Which intersect each other at point A.
[This radius must be more than half of CD and let these arc intersect each other at the point 0] - Join P and O. Then OP is the required perpendicular.
∠OPA = ∠OPB = 90°
(iii) Steps of the Construction :
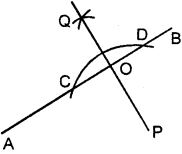
- With P as a centre, draw an arc of any suitable radius which cuts AB at points C and D.
- With C and D as a centre, draw arcs of equal radii
[The radius of these arcs must be more than half of CD and both the arcs must be drawn on the other side.]
and let these arcs intersect each other at the point Q. - Join Q and P. Let QP cut AB at the point O. Then OP is the required perpendicular.
Clearly, ∠AOP = ∠BOP = 90°
Question 4.
Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From the point P, draw a perpendicular to AB.
Answer
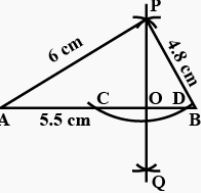
- Draw a line segment AB = 5.5 cm
- With A as centre and radius = 6 cm, draw an arc.
- With B as centre and radius = 4.8 cm draw another arc.
- Let these arcs meet each other at point P.
PA = 6 cm, PB = 4.8 - With P as a centre and some suitable radius draw an arc meeting AB at points C and D.
- With C as centre and radius more than half of CD, draw an arc.
- With D as a centre and same radius as in step 6, draw an arc.
- Let these arcs meet each other at point Q.
- Join PQ.
- The PQ meet AB at point O.
Then PO ⊥ AB i.e; ∠AOP = 90° = ∠POB.
Question 5.
Draw a line segment AB = 6.2 cm. Mark a point P in AB such that BP = 4 cm. Through point P draw perpendicular to AB.
Answer
Steps of the Construction :
- Draw a line segment AB = 6.2 cm
- Cut off BP = 4 cm
- With P as the centre and some radius draw arc meeting AB at the points C, D.
- With C, D as centres and equal radii [each is more than half of CD] draw two arcs, meeting each other at the point O.
- Join OP. Then OP is perpendicular for AB.

Concise Maths Constructions Exe-18 C for ICSE Class-8th
Question 1.
Draw a line AB = 6 cm. Mark a point P any where outside the line AB. Through the point P, construct a line parallel to AB.
Answer
Steps of the construction :

- Draw a line AB = 6 cm
- Take any point Q on the line AB and join it with the given point P.
- At point P, construct ∠CPQ = ∠PQB
- Produce CP up to any point D.
Thus, CPD is the required parallel line.
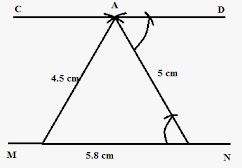
Question 2.
Draw a line MN = 5.8 cm. Locate a point A which is 4.5 cm from M and 5 cm from N. Through A draw a line parallel to line MN.
Answer
Steps of the construction :
- Draw a line MN = 5.8 cm
- With M as centre and radius = 4.5 cm, draw an arc.
- With N as centre draw another arc of radius 5 cm. These arcs intersect each other at A.
- Join AM and AN.
- At point A, draw ∠DAN = ∠ANM
- Produce DA to any point C.
Thus CAD is the required parallel line.
Question 3.
Draw a straight line AB = 6.5 cm. Draw another line which is parallel to AB at a distance of 2.8 cm from it.
Answer
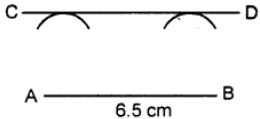
- Draw a straight line AB = 6.5 cm
- Taking point A as a centre, draw an arc of radius 2.8 cm.
- Taking B as centre, drawn another arc of radius 2.8 cm.
- Draw a line CD that touches the two arcs drawn.
Thus CD is the required parallel line.
Question 4.
Construct an angle PQR = 80°. Draw a line parallel to PQ at a distance of 3 cm from it and another line parallel to QR at a distance of 3.5 cm from it. Mark the point of intersection of these parallel lines as A.
Answer
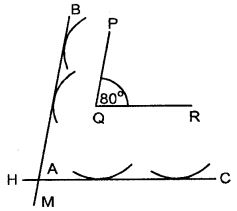
- Draw ∠PQR = 80°
- With P as centre draw an arc of radius 2 cm.
- Again with Q as a centre, draw another arc of radius 2 cm. Then BM is a line which touches the two arcs. Then BM is a line parallel to PQ.
- With Q as a centre, draw an arc of radius 3.5 cm. With R as centre draw another arc of radius 3.5 cm. Draw a line HC which touches these two arcs. Let these two parallel lines intersect at A.
Question 5.
Draw an angle ABC = 60°. Draw the bisector of it. Also draw a line parallel to BC a distance of 2.5 cm from it.
Let this parallel line meet AB at point P and angle bisector at point Q. Measure the length of BP and PQ. Is BP = PQ?
Answer
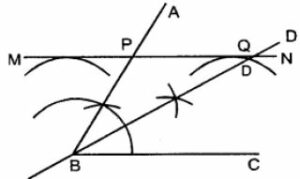
- Draw, ∠ABC = 60°
- Draw BD, the bisector of ∠ABC.
- Taking B as centre, draw an arc of radius 2.5 cm.
- Taking C as a centre, draw another arc of radius 2.5 cm.
- Draw a line MN that touches these two arcs drawn. Then MN is the required line parallel to BC.
- Let this line MN meets AB at P and bisector BD at Q.
- Measure BP and PQ.
By measurement, we see BP = PQ.
Question 6.
Construct an angle ABC = 90°. Locate a point P which is 2.5 cm from AB and 3.2 cm from BC.
Answer
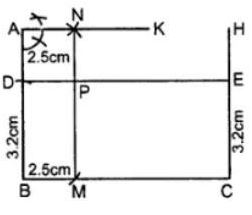
- Draw ∠ABC = 90°
- From AB, cut BD = 3.2 cm.
- Through point C, draw CH⊥BC. From CH, cut CE = 3.2. Join DE. …
- From BC cut BM = 2.5 cm.
- Through point A, draw AK ⊥ AB. From AK cut AN = 2.5 cm. …
- DE and MN intersect each other at P. Thus P is the required point which is 2.5 cm from AB and 3.2 cm from BC.
Exercise – 18 D Constructions (Using ruler and compass only) ICSE Class-8th Concise Selina Mathematics
Question 1.
Construct a quadrilateral ABCD; if:
(i) AB = 4.3 cm, BC = 5.4, CD = 5 cm, DA = 4.8 cm and angle ABC = 75°.
(ii) AB = 6 cm, CD = 4.5 cm, BC = AD = 5 cm and ∠BCD = 60°.
(iii) AB = 8 cm, BC = 5.4 cm, AD = 6 cm, ∠A = 60° and ∠B = 75°.
(iv) AB = 5 cm, BC = 6.5 cm, CD =4.8 cm, ∠B = 75° and ∠C = 120°.
(v) AB = 6 cm = AC, BC = 4 cm, CD = 5 cm and AD = 4.5 cm.
(vi) AB = AD = 5cm, BD = 7 cm and BC = DC = 5.5 cm
Answer
(i)
The figure is
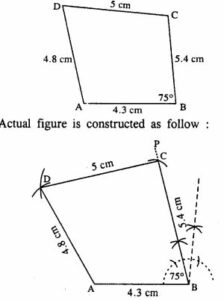
Steps :
- Draw AB = 4.3 cm.
- At B, draw ∠PBA = 75°
- Cut BC = 5.4 cm.
- From C & A, draw arcs of radii 5 cm and 4.8 cm respectively which intersect at D.
- Join AD and DC.
ABCD is the required quadrilateral.
(ii) The figure is :
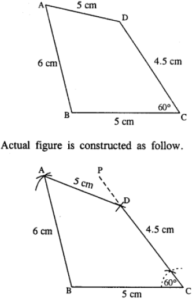
Steps :
- Draw BC = 5 cm.
- Draw ∠PCB = 60° and cut CD = 4.5 cm.
- From B and D, draw arcs of radii 6 cm and 5 cm respectively which intersect at A.
- Join AB and AD.
Thus ABCD is the required quadrilateral.
(iii) The figure is :
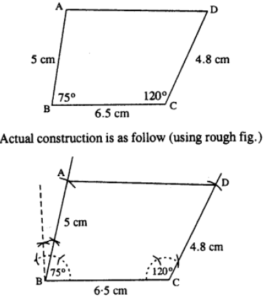
Steps :
- Draw AB = 8 cm.
- At A, draw ∠PAB = 60° and cut DA = 6 cm.
- At B, draw ∠QBA = 75° and cut BC = 5.4 cm.
- Join DC.
Thus ABCD is the required quadrilateral.
(iv) The figure is :
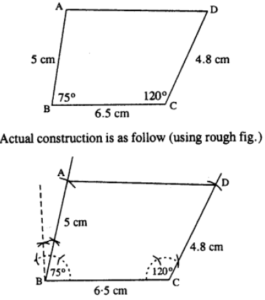
Steps :
- Draw BC = 6-5 cm.
- Draw ∠B = 75° and cut BA = 5 cm.
- Draw ∠C = 120° and cut CD = 4.8 cm.
- Join AD.
Thus ABCD is the required quadrilateral.
(v)
Steps :
- Draw AB = 6 cm.
- From A and B, draw arcs of radii 6 cm and 4 cm which cut at C.
- From A and C, draw arcs of radii 4.5 cm and 5 cm respectively which intersect at D.
- Join BC, CD, and DA. Thus ABCD is the required quadrilateral.
(vi) The figure is :
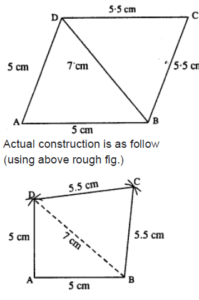
Steps :
- Draw AB = 5 cm.
- From A & B draw arcs of radii 5 cm and 7cm which intersect at D.
- From B & D draw arcs of radii 5.5 cm each which intersect at C.
- Join AD, BD, DC, and BC.
Thus ABCD is the required quadrilateral.
Question 2.
Construct a parallelogram ABCD, if :
(i) AB = 3.6 cm, BC = 4.5 cm and ∠ABC = 120°.
(ii) BC = 4.5 cm, CD = 5.2 cm and ∠ADC = 75°.
(iii) AD = 4 cm, DC = 5 cm and diagonal BD = 7 cm.
(iv) AB = 5.8 cm, AD = 4.6 cm and diagonal AC = 7.5 cm.
(v) diagonal AC = 6.4 cm, diagonal BD = 5.6 cm and angle between the diagonals is 75°.
(vi) lengths of diagonals AC and BD are 6.3 cm and 7.0 cm respectively, and the angle between them is 45°.
(vii) lengths of diagonals AC and BD are 5.4 cm and 6.7 cm respectively and the angle between them is 60°.
Answer
(i) The figure is :
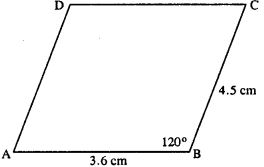
The above rough figure is used to construct the actual ||gm as follow :
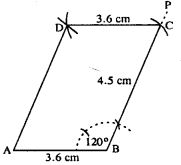
Steps :
- Draw AB = 3.6 cm.
- Draw BP such that ∠B = 120°.
- Cut BC = 4.5 cm.
- From A, draw an arc of radius 4.5 cm.
- From C, draw an arc of radius 3.6 cm. Which intersects the first arc at D.
- Join AD and CD.
Hence ABCD is the required ||gm.
(ii) The figure is :
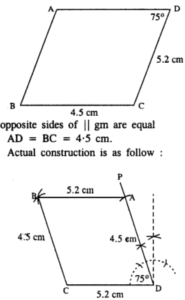
Steps :
- Draw CD = 5.2 cm.
- Draw ZCDP = 75°
- Cut DA = 4.5 cm.
- A drawn arc of radius 5.2 cm.
- From C, draw an arc of radius 4.5 cm which meets the first arc at B.
- Join AB and CB.
Thus ABCD is the required ||gm.
(iii) The figure is :
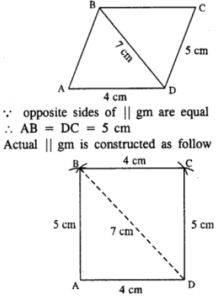
Steps :
- Draw AD = 4 cm.
- From A, draw an arc of radius 5 cm.
- From B, draw an arc of radius 4 cm.
- From D, draw an arc of radius 5 cm which intersects the first arc at C.
- Join AB, BD, BC, and CD.
Thus ABCD is the required || gm.
(iv) The figure is :
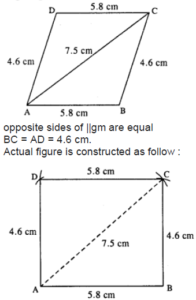
Steps:
- Draw AB = 5.8 cm.
- Draw an arc of radius 4.6 cm with centre B.
- Draw an arc of radius 7.5 cm from A which intersects the first arc at C.
- From A, draw an arc of radius 4.6 cm.
- From C, draw an arc of radius 5.8 cm which intersects the first arc at D.
- Join AD, CD, BC, and AC.
Thus ABCD is the required ||gm.
(v) The figure is :

Steps :
- Draw AC = 6.4 cm.
- Bisect AC at O.
- Draw ∠XOC = 75° and produce XO to Y.
- Cut OB = OD = 2 8 cm.
- Join AB, BC, AD, and CD.
Thus ABCD is the required ||gm.
(vi)

- Draw AC = 6.3 cm.
- Bisect AC at O.
- At O, draw ∠XOC = 45° and produce XO to Y.
- Cut OB = OD = 3.5 cm (half the diagonal 7 cm.)
- Join AB, CB, AD, and CD. Thus ABCD is the required || gm.
(vii)
Steps :
- Draw BD 6.7 cm.
- Bisect BD at O.
- At O, draw ∠XOD = 60° and produce XO to Y.
- Cut OA = OC = 2.7 cm (half the diagonals 5.4 cm)
- Join AB, AD, BC, and CD.
Thus ABCD is the required ||gm.
Question 3.
Construct a rectangle ABCD ; if :
(i) AB = 4.5 cm and BC = 5.5 cm.
(ii) BC = 61 cm and CD = 6.8 cm.
(iii) AB = 5.0 cm and diagonal AC = 6.7 cm.
(iv) AD = 4.8 cm and diagonal AC = 6.4 cm.
(v) each diagonal is 6 cm and the angle between them is 45°.
(vi) each diagonal is 5.5 cm and the angle between them is 60°.
Answer
(i)
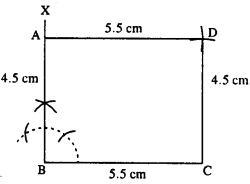
Steps :
- Draw BC = 5.5 cm.
- At B, draw ∠XBC = 90°
- Cut BA = 4.5 cm.
- From A, draw an arc of radius 5.5 cm.
- From C, draw an arc of radius 4 5 cm which meets the first arc at D.
- Join AD and CD.
Thus ABCD is the required rectangle.
(ii)
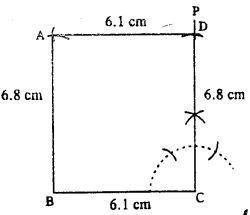
Steps:
- Draw BC = 6.1 cm.
- At C, draw ∠PCB = 90°.
- Cut CD = 6.8 cm.
- Draw an arc of radius 6.8 cm from B.
- From D, draw an arc of radius 6.1 cm which meets the first arc at A.
- Join AB and AD.
Thus ABCD is the required rectangle.
(iii)
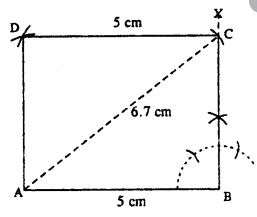
Steps :
- Draw AB = 5 cm.
- At B, draw ∠XBA = 90°.
- From A, draw an arc of radius 6.7 cm which meets XB at C.
- From C, draw an arc of a radius of 5 cm.
- From A, draw an arc of radius equal to BC which meets the first arc at D.
- Join AD and CD. Thus ABCD is the required rectangle.
(iv)
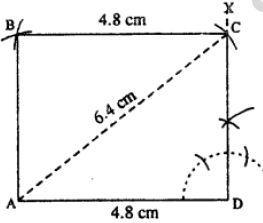
Steps :
- Draw AD = 4.8 cm.
- At D, draw ∠XDA = 90°.
- From A, draw an arc of radius 6-4 cm which meets DX at C.
- From A, draw an arc of radius equal to DC.
- From C, draw an arc of radius 4.8 cm which meets the first arc at B.
- Join AB and CB. Thus ABCD is the required rectangle.
(v)
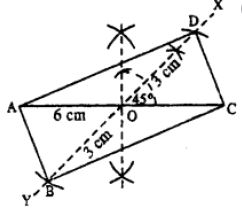
Steps :
- Draw AC = 6 cm.
- Bisect AC at O.
- At O, draw ∠XOC = 45° and produce XO to Y.
- Cut OB = OD = 3 cm (half the diagonal 6 cm)
- Join AB, CB, AD, and CD.
Thus ABCD is the required rectangle.
(vi)
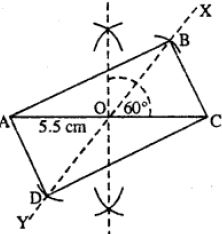
Steps :
- Draw AC = 5.5 cm.
- Bisect AC at O.
- At O, draw ∠XOC = 60° and produce XO to Y.
- Cut OB = OA and OD = OA (half the diagonal AC).
- Join AB, BC, AD, and CD.
Thus ABCD is the required rectangle.
Question 4.
Construct a rhombus ABCD, if ;
(i) AB = 4 cm and ∠B = 120°.
(ii) BC = 4.7 cm and ∠B = 75°.
(iii) CD = 5 cm and diagonal BD = 8.5 cm.
(iv) BC = 4.8cm, and diagonal AC = 7cm.
(v) diagonal AC = 6 cm and diagonal BD = 5.8 cm.
(vi) diagonal AC = 4.9 cm and diagonal BD = 6 cm.
(vii) diagonal AC = 6.6 cm and diagonal BD = 5.3 cm.
Answer
(i)
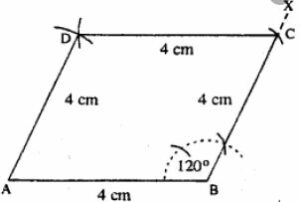
Steps :
- Draw AB = 4 cm.
- At B, draw ∠XBA = 120°
- Cut BC = 4 cm.
- Draw arcs of radii 4 cm each from A and C which intersect at D.
- Join CD and AD.
Thus ABCD is the required rhombus.
(ii)
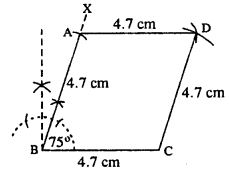
Steps :
- Draw BC = 4.7 cm.
- At B, draw ∠XBC = 75°
- Cut BA = 4.7 cm.
- From A and C, draw arcs of radii 4.7 cm each which intersect at D.
- Join AD and CD.
Thus ABCD is the rhombus.
(iii)
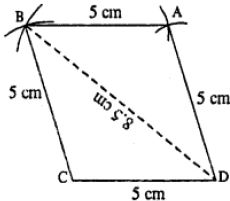
Steps :
- Draw CD = 5 cm.
- From C & D draw arcs of radii 5 cm and 8.5 cm respectively which intersect at B.
- From B and D, draw arcs of radii 5 cm each which intersect at A.
- Join AB and AD.
Thus ABCD is the required rhombus.
(iv)
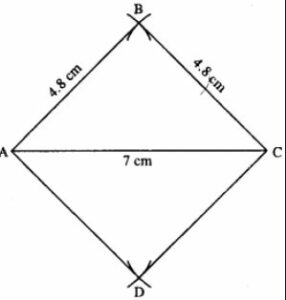
Steps :
- Draw AC = 7 cm.
- Draw arcs of radii 4.8 cm each from A and C which intersect at B.
- From A & C again draw arcs of radii 4.8 cm each which intersect at D.
- Join AB, BC, AD, and CD.
Thus ABCD is the required rhombus.
(v)
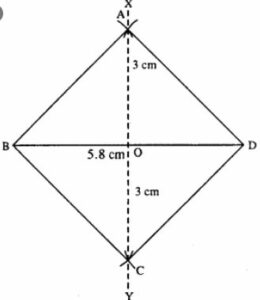
Steps :
- Draw BD = 5.8 cm.
- Draw perpendicular bisector XY of BD.
- Cut OA = OC = 3 cm (half the diagonal 6 cm)
- Join AB, AD, BC, and CD.
Thus ABCD is the required rhombus.
(vi)
Steps :
- Draw AC = 4.9 cm.
- Draw perpendicular bisector XY of AC.
- Cut OB = OD = 3 cm (half the diagonal 6 cm)
- Join AB, BC, AD, and CD.
Thus ABCD is the required rhombus.
(vii)
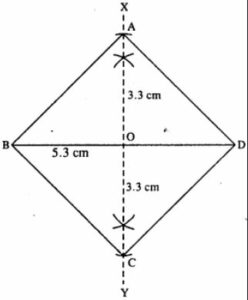
Steps :
- Draw BD = 5.3 cm.
- Draw perpendicular bisector XY of BD.
- Cut OA = OC = 3.3 cm (half the diagonal 6.6 cm)
- Join AB, AD, BC, and CD.
Thus ABCD is the required rhombus.
Question 5.
Construct a square, if :
(i) its one side is 3.8 cm.
(ii) its each side is 4.3 cm.
(iii) one diagonal is 6.2 cm.
(iv) each diagonal is 5.7 cm.
Answer
(i)
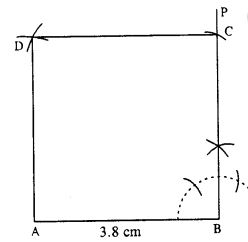
Steps :
- Draw AB = 3.8 cm.
- At B, draw ∠PBA = 90°.
- Cut BC = 3.8 cm.
- From A and C, draw arcs of radii 3.8 cm each which intersect at D.
- Join AD and CD.
Thus ABCD is the required square.
(ii)

Steps :
- Draw AB = 4.3 cm.
- Draw ∠PAB = 90° at A.
- Cut AD = 4.3 cm.
- From B and D, draw arcs of radii 4.3 cm each which intersect at C.
- Join AD, BC, and CD.
Hence ABCD is the required square.
(iii)
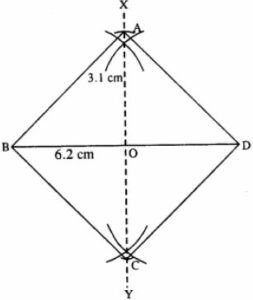
Steps :
- Draw BD = 6.2 cm.
- Draw perpendicular bisector XY of BD.
- Cut OA = OC = 3.1 cm (half the diagonal)
- Join AB, AD, BC, and CD.
Thus ABCD is the required square.
(iv)
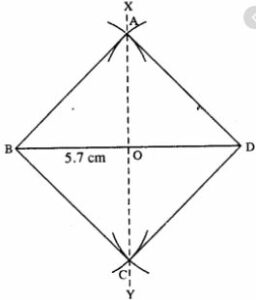
Steps :
- Draw BD = 5.7 cm.
- Draw perpendicular bisector XY of BD.
- From 0, draw arcs of radii equal to OB which cuts XY at A and C.
- Join AB, AD, BC, and CD.
Thus ABCD is the required square.
Question 6.
Construct a quadrilateral ABCD in which ; ∠A = 120°, ∠B = 60°, AB = 4 cm, BC = 4.5 cm and CD = 5 cm.
Answer
The figure is :
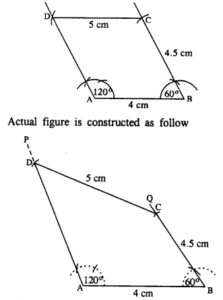
Steps :
- Draw AB = 4 cm.
- At A, draw ∠PAB = 120°.
- At B, draw ∠QBA = 60°.
- From BQ, cut BC = 4.5 cm.
- From C, draw an arc of radius 5 cm which meets AP at D.
- Join CD.
Thus ABCD is the required quadrilateral.
Question 7.
Construct a quadrilateral ABCD, such that AB = BC = CD = 4.4 cm, ∠B = 90° and ∠C = 120°.
Answer
The figure is :
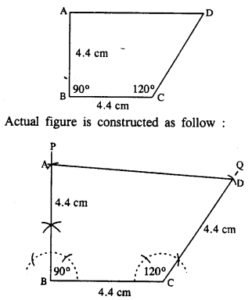
Steps :
- Draw BC = 4.4 cm.
- At B, draw ∠PBC = 90°.
- Cut BA = 4.4 cm.
- At C, draw ∠QCB = 120°.
- Cut CD = 4.4 cm.
- Join AD.
Thus ABCD is the required quadrilateral.
Question 8.
Using ruler and compasses only, construct a parallelogram ABCD, in which : AB = 6 cm, AD = 3 cm and ∠DAB = 60°. In the same figure draw the bisector of angle DAB and let it meet DC at point P. Measure angle APB.
Answer
Steps :
- Draw AB = 6 cm.
- At A draw ∠QAB = 60°.
- From AQ cut AD = 3 cm.
- From D, draw an arc of radius 6 cm.
- From B, draw an arc of radius 3 cm which meets the first arc at C.
- Join CD and BC.
Thus ABCD is the required ||gm. - Bisect ∠DAB, so that bisector meets CD at P.
- Join PB and measure ZAPB.
∴ ∠APB = 90°.
Question 9.
Draw a parallelogram ABCD, with AB = 6 cm, AD = 4.8 cm and ∠DAB = 45°. Draw the perpendicular bisector of side AD and let it meet AD at point P. Also draw the diagonals AC and BD ; and let they intersect at point O. Join O and P. Measure OP.
Answer
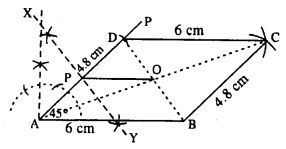
Steps :
- Draw AB = 6 cm.
- Draw ∠PAB = 45°.
- Cut AD = 4.8 cm.
- From D, draw an arc of radius 6 cm.
- From B, draw an arc of radius 4.8 cm which meets the first arc at C.
- Join BC, CD, AD.
Thus ABCD is the required ||gm. - Draw perpendicular bisector XY of AD which cuts AD at P.
- Join AC and BD which intersect at O.
- Join OP and measure it.
OP = 3 cm.
Question 10.
Using ruler and compasses only, construct a rhombus whose diagonals are 8 cm and 6 cm. Measure the length of its one side.
Answer
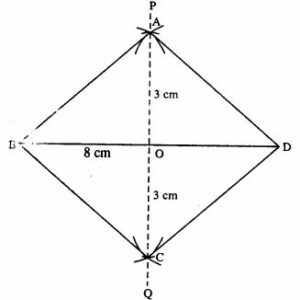
Steps :
- Draw BD = 8 cm.
- Draw perpendicular bisector PQ of BD.
- Cut OA = OC = 3 cm [half the diagonal 6 cm]
- Join AB, AD, BC, and CD.
- Measure side AB which is 5 cm.
Thus ABCD is the required rhombus.
— End of Constructions ICSE Class-8th Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -8




